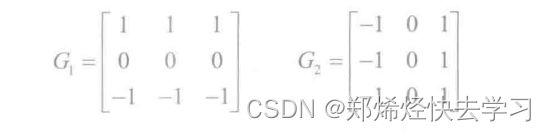OpenCV入门(四)——边缘检测
目录
0x01 梯度算子
0x02 一阶微分算子
0x03 二阶微分算子
0x04 图像差分运算
0x05 非极大值抑制
0x06 基本边缘算子——Sobel
0x07 基本边缘算子——Laplace
0x08 基本边缘检测算子——Roberts
0x09 基本边缘检测算子——Prewitt
边缘检测的概念:检测识别出图像图像中亮度变化剧烈的像素点构成的集合。
目标物体形成边缘存在以下几种情形:
-
目标物呈现在图像上的不同物体平面上,深度不连续。
-
目标物本身平面不同,表面方向不连续。
-
目标物材料不均匀,表面反射光不同。
-
目标物受外部场景光影响不一。
根据边缘形成的原理,对图像的各像素点进行求微分或二阶微分可以检测出灰度变化明显的点。通常情况下边缘检测分为以下三个类型:
-
一阶微分为基础的边缘检测:通过计算图像的梯度值来检测图像边缘。
Sobel算子、Prewitt算子、Roberts算子以及差分边缘检测。
-
二阶微分为基础的边缘检测:通过寻求二阶导数中的过零点来检测边缘。
拉普拉斯算子、高斯拉普拉斯算子、Canny算子边缘检测图。
-
混合一阶与二阶微分为基础的边缘检测:综合利用一阶微分与二阶微分特征
Marr-Hildreth边缘检测算子。
0x01 梯度算子
数字图像的简单一阶微分运算,由于其具有固定的方向性,只能检测特定的某一方向的边缘,所以不具有普遍性。
克服以上一阶导数的缺点,我们定义图像的梯度为梯度算子,它是图像处理中最常用的一阶微分算法。图像梯度最重要的性质是梯度的方向是在图像灰度最大变化率上,恰好可以反映出图像边缘上的灰度变化。
梯度算子总是指向变换最剧烈的方向,在图像处理中,梯度向量总是与边缘正交,梯度方向为:
0x02 一阶微分算子
利用了图像在边缘处的阶跃性,即图像梯度在边缘处取得极大值的特性来进行边缘检测。对于一幅二维的数字图像而言,它需要完成x与y两个方向上的微分,所以就有如下的公式分别求出x和y两个方向上的偏微分,最终得到的梯度是一个矢量,具有方向与模:
0x03 二阶微分算子
图像的边缘时图像的一阶微分极大值的像素点值,根据函数微分特性,该像素点值的二阶微分为0。图像边缘检测中根据二阶微分在边缘处出现零点这个特性来实现边缘检测。用拉普拉斯算子计算:
0x04 图像差分运算
void diffOperation(const cv::Mat srcImage, cv::Mat& edgeXImage, cv::Mat& edgeYImage)
{
cv::Mat tempImage = srcImage.clone();
int nRows = tempImage.rows;
int nCols = tempImage.cols;
for (int i = 0; i < nRows - 1; i++)
{
for (int j = 0; j < nCols - 1; j++)
{
//计算垂直边缘
edgeXImage.at(i, j) = abs(tempImage.at(i + 1, j) - tempImage.at(i, j));
//计算水平边缘
edgeYImage.at(i, j) = abs(tempImage.at(i, j + 1) - tempImage.at(i, j));
}
}
}
cv::Mat edgeXImage(image_reduced.size(),image_reduced.type());
cv::Mat edgeYImage(image_reduced.size(),image_reduced.type());
//计算差分图像
diffOperation(image_reduced, edgeXImage, edgeYImage);
cv::imshow("edgeXImage", edgeXImage);
cv::imshow("edgeYImage", edgeYImage);
cv::Mat edgeImage(image_reduced.size(),image_reduced.type());
//水平与垂直边缘图像叠加
cv::addWeighted(edgeXImage,0.5, edgeYImage,0.5,0.0, edgeImage);
cv::imshow("Together", edgeImage); 本质其实就是找到阈值变化在x方向和y方向上的突变点,也就是与相邻的点进行做差比较,将变化较大的点画出来。
0x05 非极大值抑制
图像梯度矩阵中的元素值越大,说明图像中该点的梯度值越大,但这并不能将其判断为该点处的边缘。(存在误差)非极大值一直操作可以剔除伪边缘信息,被广泛应用于图像边缘检测中。
原理:是通过像素邻域的局部最优值,将非极大值点所对应的灰度值设为背景像素点,如像素邻域区域满足梯度值局部最优值则判断为该像素的边缘,对其余非极大值的相关信息进行抑制,利用该准则可以剔除大部分非边缘点。
就比如说我们取中间点p0,梯度方向与其邻域交点为PM、PN,根据非极大值抑制原理,我们需要先确定P0像素值是否满足领域内最大,需要判断P0与邻域像素值和梯度方向PM与PN对应的值。所以我们要把当前位置的梯度值,在邻域内先比较一圈,如果是最大的,那么就开始下一步,我们比较P0与PM与PN的最大值,同时还得考虑梯度方向的变化。
总结来说:若满足P0像素值是邻域内的最大值且梯度值最大,可判断该点是边缘像素点,否则P0像素点不是局部最优值,可剔除伪边缘。(这样就可以确定到底是不是真的边界了)
0x06 基本边缘算子——Sobel
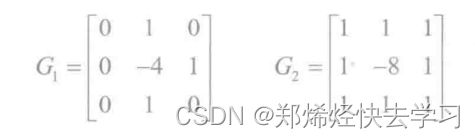
Sobel算子是应用广泛的离散微分算子之一,常用于图像处理中的边缘检测,计算图像灰度函数的近似梯度。利用图像像素点Sobel算子计算出相应的梯度向量及向量的范数,基于图像卷积来实现在水平方向与垂直方向检测对应方向上的边缘。对于源图像与奇数Sobel水平核Gx、垂直核Gy进行卷积可计算水平与垂直变换,当内核大小为3*3时,Gx与Gy为下式:
对图像中每一点结合卷积后的结果求出近似梯度幅度G:
Sobel算子在进行边缘检测时效率较高,当对精度要求不是很高时,是一种较为常用的边缘检测方法。
缺点在于:
Sobel算子对沿x轴和y轴的排列表示得较好,但是对于其他角度得表示却不够精确,这时候我们可以使用Scharr滤波器。Scharr滤波器得水平和垂直核因子:
(一)实现非极大值抑制Sobel检测:
实现步骤:非极大值抑制实现Sobel竖直细化边缘
-
将图像转为32位浮点型数据,定义水平或垂直方向的Sobel算子。
-
使用filter2D完成图像与算子的卷积操作,计算卷积结果的梯度幅值。
-
自适应计算出梯度幅值阈值,阈值设置不梯度幅值的均乘以4,根据阈值对水平或垂直的领域区梯度进行比较。
-
判断当前邻域梯度是否大于水平或垂直邻域梯度,自适应完成边缘检测出二值化图像的操作。
bool SobelVerEdge(cv::Mat srcImage, cv::Mat& resultImage)
{
CV_Assert(srcImage.channels() == 1);
srcImage.convertTo(srcImage, CV_32FC1);
// 水平方向的 Sobel 算子
cv::Mat sobelx = (cv::Mat_(3,3) << -0.125, 0, 0.125,
-0.25, 0, 0.25,
-0.125, 0, 0.125);
cv::Mat ConResMat;
// 卷积运算
cv::filter2D(srcImage, ConResMat, srcImage.type(), sobelx);
// 计算梯度的幅度
cv::Mat graMagMat;
cv::multiply(ConResMat, ConResMat, graMagMat);
// 根据梯度幅度及参数设置阈值
int scaleVal = 4;
double thresh = scaleVal * cv::mean(graMagMat).val[0];
cv::Mat resultTempMat = cv::Mat::zeros(
graMagMat.size(), graMagMat.type());
float* pDataMag = (float*)graMagMat.data;
float* pDataRes = (float*)resultTempMat.data;
const int nRows = ConResMat.rows;
const int nCols = ConResMat.cols;
for (int i = 1; i != nRows - 1; ++i) {
for (int j = 1; j != nCols - 1; ++j) {
// 计算该点梯度与水平或垂直梯度值大小比较结果
bool b1 = (pDataMag[i * nCols + j] > pDataMag[i *
nCols + j - 1]);
bool b2 = (pDataMag[i * nCols + j] > pDataMag[i *
nCols + j + 1]);
bool b3 = (pDataMag[i * nCols + j] > pDataMag[(i - 1)
* nCols + j]);
bool b4 = (pDataMag[i * nCols + j] > pDataMag[(i + 1)
* nCols + j]);
// 判断邻域梯度是否满足大于水平或垂直梯度
// 并根据自适应阈值参数进行二值化
pDataRes[i * nCols + j] = 255 * ((pDataMag[i *
nCols + j] > thresh) &&
((b1 && b2) || (b3 && b4)));
}
}
resultTempMat.convertTo(resultTempMat, CV_8UC1);
resultImage = resultTempMat.clone();
return true;
} (二)实现图像直接卷积实现Sobel:
原理:图像直接卷积Sobel边缘检测实现比较简单,首先定义水平或垂直方向的Sobel核因子,直接对源图像进行窗遍历,计算窗内的领域梯度幅值,然后根据梯度模场进行二值化操作,完成图像的水平或垂直方向的边缘检测。
//图像直接卷积
bool sobelEdge(const cv::Mat& scrImage, cv::Mat& resultImage, uchar threshold)
{
CV_Assert(scrImage.channels() == 1);
//初始化水平核因子
cv::Mat sobelx = (cv::Mat_(3, 3) << 1, 0, -1, 2, 0, -2, 1, 0, -1);
//初始化垂直因子
cv::Mat sobely = (cv::Mat_(3, 3) << 1, 2, 1, 0, 0, 0, -1, -2, -1);
resultImage = cv::Mat::zeros(scrImage.rows - 2, scrImage.cols - 2, scrImage.type());
double edgeX = 0;
double edgeY = 0;
double graMag = 0;
for (int k = 1; k < scrImage.rows - 1; ++k)
{
for (int n = 1; n < scrImage.cols - 1; ++n)
{
edgeX = 0;
edgeY = 0;
//遍历计算水平与垂直梯度
for (int i = -1; i <= 1; ++i)
{
for (int j = -1; j <= 1; ++j)
{
edgeX += scrImage.at(k + 1, n + j) * sobelx.at(1 + i, 1 + j);
edgeY += scrImage.at(k + i, j + i) * sobely.at(1 + i, 1 + j);
}
}
//计算梯度模长
graMag = sqrt(pow(edgeY, 2) + pow(edgeX, 2));
//二值化
resultImage.at(k - 1, n - 1) = ((graMag > threshold) ? 255 : 0);
}
}
return 0;
} (三)实现图像卷积下非极大值抑制Sobel:
非极大值抑制虽然能够较好地剔除虚假边缘点,但对于某些特定场景下的边缘并不使用,例如污损文本字符识别。
bool sobelOptaEdge(const cv::Mat& srcImage, cv::Mat& resultImage, int flag)
{
CV_Assert(srcImage.channels() == 1);
// 初始化sobel水平核因子
cv::Mat sobelX = (cv::Mat_(3, 3) << 1, 0, -1,
2, 0, -2,
1, 0, -1);
// 初始化sebel垂直核因子
cv::Mat sobelY = (cv::Mat_(3, 3) << 1, 2, 1,
0, 0, 0,
-1, -2, -1);
// 计算水平与垂直卷积
cv::Mat edgeX, edgeY;
filter2D(srcImage, edgeX, CV_32F, sobelX);
filter2D(srcImage, edgeY, CV_32F, sobelY);
// 根据传入参数确定计算水平或垂直边缘
int paraX = 0;
int paraY = 0;
switch (flag)
{
case 0: paraX = 1;
paraY = 0;
break;
case 1: paraX = 0;
paraY = 1;
break;
case 2: paraX = 1;
paraY = 1;
break;
default: break;
}
edgeX = abs(edgeX);
edgeY = abs(edgeY);
cv::Mat graMagMat = paraX * edgeX.mul(edgeX) + paraY * edgeY.mul(edgeY);
// 计算阈值
int scaleVal = 4;
double thresh = scaleVal * cv::mean(graMagMat).val[0];
resultImage = cv::Mat::zeros(srcImage.size(), srcImage.type());
for (int i = 1; i < srcImage.rows - 1; i++)
{
float* pDataEdgeX = edgeX.ptr(i);
float* pDataEdgeY = edgeY.ptr(i);
float* pDataGraMag = graMagMat.ptr(i);
// 阈值化和极大值抑制
for (int j = 1; j < srcImage.cols - 1; j++)
{
if (pDataGraMag[j] > thresh && (
(pDataEdgeX[j] > paraX * pDataEdgeY[j] && pDataGraMag[j] >
pDataGraMag[j - 1] && pDataGraMag[j] > pDataGraMag[j + 1]) ||
(pDataEdgeY[j] > paraY * pDataEdgeX[j] && pDataGraMag[j] >
pDataGraMag[j - 1] && pDataGraMag[j] > pDataGraMag[j + 1])))
resultImage.at(i, j) = 255;
}
}
return true;
} 以上就是三种sobel算法。可以根据实际场景的需求来实现相应的sobel边缘功能。第二种方法的伪边缘比较多,所以得出非极大值抑制可以有效地解决这一问题的结论。
如何使用:
cv::Mat image(608, 608,CV_8UC3);
image = cv::imread("./image/labixiaoxin.jpg", cv::IMREAD_GRAYSCALE); //
//灰度图像
cv::namedWindow("原图",cv::WINDOW_FREERATIO);
cv::imshow("原图", image);
cv::Mat resultImage;
//非极大值抑制细化数值sobel检测
SobelVerEdge(image, resultImage);
cv::namedWindow("非极大值抑制", cv::WINDOW_FREERATIO);
cv::imshow("非极大值抑制", resultImage);
//图像直接卷积
cv::Mat resultImage2;
sobelEdge(image,resultImage2,100);
cv::namedWindow("非极大值抑制", cv::WINDOW_FREERATIO);
cv::imshow("图像直接卷积", resultImage2);
//图像卷积下非极大值抑制
cv::Mat resultImage3;
sobelEdge(image, resultImage3,2);
cv::imshow("图像卷积+非极大值", resultImage3);效果:
Opencv提供的Sobel函数:
void sobel(InputArray src, //输入图像
OutputArray dst, //输出图像
int ddepth, //输出图像深度
int dx, //x方向的导数运算参数
int dy, //y方向的导数运算参数
int ksize = 3, //内核大小,设置为奇数
double scale = 1, //缩放导数的比例常数
double delta = 0, //可选的增量常数
int borderType = BORDER_DEFAULT //判断图像边界模式
)sobel核因子大小为3,内核因子计算会产生一定的误差,opencv也有提供更精确的内核因子以及Scharr函数,其计算的时间复杂度与sobel差不多。
0x07 基本边缘算子——Laplace
拉普拉斯算子是最简单的各向同性二阶微分算子,具有旋转不变性。根据函数微分特性,该像素点值的二阶微分为0的点为边缘点,也就是边界点(因为在这个时候的阈值跳变为最大值,二次求导为0),对于二维图像f(x,y),它的二阶导数定义为:
对于二维离散图像而言,图像的Laplace可表示为下式:
根据离散的Laplace的表达式,可以得到其模板的表现形式:
这种算法常用于锐化处理,对于图像中灰度变化剧烈的区域,拉普拉斯算子能实现其边缘检测;拉普拉斯算子利用二次微分特性与峰值间的过零点来确定边缘的位置,对奇异点或边界的更为敏感。
那么针对原始图像f(x,y),瑞华操作可以通过拉普拉斯算子对源图像进行处理,进行微分运算操作后产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加进而产生锐化图像。
其中t为领域中心比较系数,拉普拉斯算子锐化操作通过比较领域的中心像素与他所在的领域内的其他像素的平均灰度来确定相应的变换方式。当t<=0时,中心像素的灰度被进一步降低;相反,当t>0,中心像素的灰度被进一步提高。
cv::Mat image(608, 608,CV_8UC3);
image = cv::imread("./image/cross.jpg", cv::IMREAD_GRAYSCALE);
cv::namedWindow("原图",cv::WINDOW_FREERATIO);
cv::imshow("原图", image);
cv::Mat resultImage;
//高斯平滑
cv::GaussianBlur(image, image,cv::Size(3,3),0,0,cv::BORDER_DEFAULT);
//拉普拉斯变换
cv::Laplacian(image, resultImage,CV_16S,3);
cv::convertScaleAbs(resultImage, resultImage);
cv::imshow("after",resultImage);0x08 基本边缘检测算子——Roberts
Roberts算子是利用局部差分寻找边缘的一种算子,是最简单的边缘检测算子。Roberts算子利用对角线方向相邻两像素之差近似梯度幅值来检测边缘,检测垂直边缘的效果要优于其他方向边缘,定位精度高,但对噪声的抑制能力比较若,边缘检测算子检查每个像素的领域并对灰度变化了进行量化,同时也包含方向的确定。
对于原始图像f(x,y),Roberts边缘检测输出图像为g(x,y),图像的Roberts边缘检测可用下式来表示:
根据上面的公式,可以得到Roberts算子模板为:
代码如下:
cv::Mat roberts(cv::Mat srcImage)
{
cv::Mat dstImage = srcImage.clone();
int nRows = dstImage.rows;
int nCols = dstImage.cols;
for(int i=0;i(i,j)-srcImage.at(i+1,j+1)*(srcImage.at(i,j)-srcImage.at(i+1,j+1));
int t2 = (srcImage.at(i+1,j)-srcImage.at(i,j+1)*(srcImage.at(i+i,j)-srcImage.at(i,j+1));
//计算对角线像素差
dstImage.at(i,j)=(uchar)sqrt(t1+t2);
}
}
return dstImage;
} 0x09 基本边缘检测算子——Prewitt
Prewitt算子是一阶边缘检测微分算子,对噪声具有抑制作用。原理与sobel相似,都是在图像空间利用两个方向模板与图像进行领域卷积来完成,分别对水平与垂直方向边缘进行检测。这个算法,边缘定位精度不如Roberts算子,实现方法与sobel类似,但是实现的功能的差距很大。。所以,一带而过吧。
对于最后的输出边缘图像,可根据G=max(Gx,Gy)或G=Gx+Gy得到,凡灰度新值大于或等于阈值的像素点就认为是边缘点,即选择适当的阈值T。若G>=T,则对应像素点为边缘点。
其实我觉得这个方法不大实际,给一个固定的阈值,往往都是容易出错的。。模板算子:
不写代码了,用不上。。
那就先介绍完这些基本的算子吧,其实我觉得对于像跑比赛等小型赛道,用上面的处理就应该可以了,对于复杂一些的图像,才需要用到我下一篇要总结的一些成熟的算子。那么就到这吧,希望以后写博客效率高一点!!