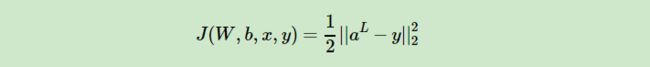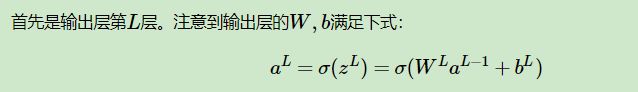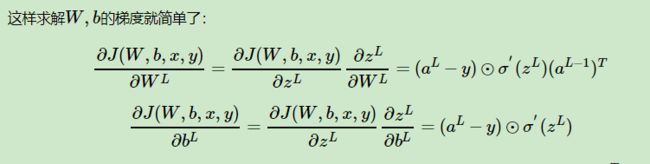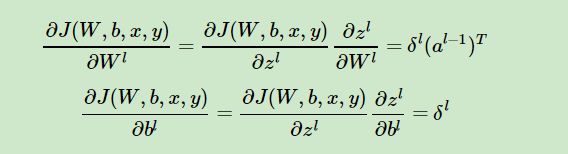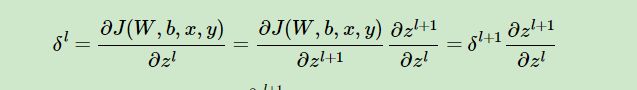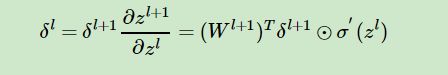深度学习——DNN反向传播

理解链式求导

          网站链接：https://www.bilibili.com/video/av10435213?from=search&seid=5523894613383510820

          膜拜大神，我就知道，这位大神不会让我失望，这视频弄得我无话可说，想理清楚的思路全都有，最关键的是要学习大神的思考方法——那惊为天人的可视化。

为什么写这篇文章：

          看到了一篇很具有逻辑性的证明博客，自己又有很多东西想记一下，不然忘了也不知道去哪儿找。

 

DNN反向传播

1.导论

     以前写过一篇总结性的文章，照着《深度学习与神经网络》这本书以及别人的笔记边学边写，结果发现自己处于半懂半不懂的状态，那时候把代码看的差不多，并码了一遍以后，就没有放在心上。直到自己看到卷积，再次面向CNN的反向传播算法，才突然醒悟，自己应该去干什么。

     我或者很多人，在学习数学时都有一个误区，很多数学的定理都是推导证明出来的，但是我们习惯拿来直接用，忘掉了怎么去证明。当我去看代码时，反向传播体现的仅仅是基于链式法则得出的结论，可是他到底是什么，一个模糊的概念让我心头很是不爽，所以，在看卷积的方向传播前，我必须将全连接的反向传播（DNN）看懂。

2.误区

    对于我个人而言，没有人系统带着学习，全靠自己，所以很容易去想错一些事儿。比如说，在学习反向传播以前，很多人一定学到了梯度下降这个算法，它很简单，但是当我把他和反向传播算法联系到一起时，我懵了，梯度下降体现在哪里？其实只要研究下这个算法的代码，思路会很清晰，但是我看完后依旧有这么一个误区——总是想当然以为因变量是X,那我求导不应该对X吗？然后全乱了....现在想想是真的傻。变量是谁？很明显，这里应该是权重和偏置（w和b），随机给他们一个值，然后朝着谷底的方向更新他们，使得误差函数最小。这才是他们结合的本来面目。

   如果看完《深度学习和神经网络》这本书，你会很清晰的知道，随机初始化这个说法太不严谨，服从标准正太分布的初始化不一定是最好的，当然，这里我们的重点应该放在更新上面。（我想试着用于语言描述这个过程，因为我发现我看过的资料里并没有人这么做，但是对于当时的我，需要这么一篇有逻辑性的文章，而不是仅仅有证明的，缺乏思考的资料）

3.轻松阅读

    首先，求导或者求偏导意味着什么，个人认为联系到变化率三个字是最为完美的，因为无论是学习求导时还是推导基本函数的导数时，都是在围绕变化率这三个字。变化率越大，求导结果越大，也可以变相理解为，重要程度也越大，那我为了使损失函数误差最小，需要更新自变量——权重和偏置（w和b），我要怎么更新？当然是越重要的更新的越多，不重要的更新的越少。 

    上面那句话可以从这个角度理解：

（1）.越重要为什么更新的越多？

      首先你必须要有这个意识，越重要更新越多是我在写这个算法时就考虑好的，即这个重要程度可不是我每次都人为去筛选的，是代码基于数据自己选择的。通俗来讲，少年，深度学习基于什么？Machine  learning,机器学习，机器学习最大的好处是什么，最最通俗来说，机器自己去学习。机器为什么可以做到这样？因为他从数据里面学习到了“经验”。那，这个重要程度基于什么确定？我上面已经论述过了，把（变化率越大，求导结果越大，也可以变相理解为，重要程度也越大）这句话倒过来，难道不成立？结合上图，我为了让损失函数更快的接近最小值，一定沿着变化率最快的方向改变。

（2）不重要更新的少

       上面懂了，这个就很容易了。

4.数学之美

      长篇大论只是为了将抽象的数学平民化，但是却忽略了它本身简介、巧妙的特性。个人对数学理论钻研不够深刻，所以下文是基于大佬们的推导自己瞎琢磨的。

 4.1 目标函数

       做过优化的同学应该知道目标函数这个概念，在这里我们的损失函数就是目标函数（原谅我懒不想手打公式，所以此处...截图）。建议：本着严谨的态度，希望真的在看的同学看完以后，再去找另外的博客或书籍拜读，因为证明是没问题的，但是证明过程中形式会有一点问题，会导致理解出现一点疑惑。（但是这个证明形式我最喜欢，很有逻辑性，不像我以前看的....如果你看我以前的博客，写的简直...但是为了记住这些经历，我还是留着吧）

        举一个不太好看（截图原因）的例子：

（1）

（2）

                  

        两个代价函数都选择的平方和代价函数，但是表现形式是不同的，一个基于实际情况按照累加的方式，一个就是单纯的函数，但是在证明时你不能说谁对谁错，自己把握就好。

      （继续）我们的目的是将这个损失函数最小化，怎么最小化？按照上文，要改变自变量——权值和偏置（w和b）。怎么改变？求偏导啊，按照偏导改变。所以，首先我们分别对这两个自变量求偏导。

                    

            

         链式求导法则，如果看过上面大佬视频的应该不难理解。

         为了方便，做了如下替换：

                                  

         很显然，为了求偏导，我必须知道(额，自己看图应该看出来了吧...)，那我怎么求，当然是巧妙地利用数学原理啊。

                          

          这个公式不仅告诉了我们怎么求，还将整个神经网络连接了起来。接着求谁？（应该看得出来....）

               

         上式求偏导后带入上上式得：

                                            

 

        至此，我最最想说得已经论述完了，这就是反向传播的精髓，至于代码怎么实现？一定不仅仅于此。最难的懂了其他就很好说了，推荐去看看         （http://neuralnetworksanddeeplearning.com/about.html）

       里面有代码，也有反向传播的讲解，但是没有逻辑性，很散乱，不然我以前早融会贯通了.......也就不会写出以前那么烂的博客了。

 

（此处，重点）

参考大神博客：https://www.cnblogs.com/pinard/p/6422831.html，证明过程是整理这里的，很具有逻辑性，里面也有代码怎么实现得语言叙述，建议没有打过代码的同学看看。