【刷题日记】笔试经典编程题目（一）

大家好，我是白晨，一个不是很能熬夜，但是也想日更的人✈。如果喜欢这篇文章，点个赞，关注一下白晨吧！你的支持就是我最大的动力！

前言

---

虽然还有很多课，但是也不能忘了写编程题呀。最近，白晨终于忙完了考试，有时间总结一下自己所做过的题了。

这次白晨总结了一下大厂笔试时所出的经典题目，题型包括贪心算法，动态规划，双指针等，难度并不是很难，但是都是很有代表性的经典题目，适合大家复习和积累经验。

大家可以自己先试着自己挑战一下，再来看解析哟！

---

笔试编程题（一）

---

1.组队竞赛

---

原题链接：组队竞赛

这道题就是经典的贪心算法，乍一看上去什么都不会，但是看完答案后却想上吊的那种。

• 贪心算法

如果我们选不了最大值，那么我们可以将所有选手水平值按照从大到小排序，从第二个开始，每隔两个选一个。这样就做到了水平的最大化，并且选中的水平值前面总有一个比自己大的，做到了一一对应。利用了选不了最大，就选第二大的思想。

比如例题中， 5 2 8 5 1 5 --> 8 5 5 5 2 1，从第二个开始选，每隔两个一选，选中 5 ，5，所以 5 + 5 =10，就为最大水平值。

#include 
#include
#include
using namespace std;

int main()
{
    // 用long long存，防止溢出
    long long  ret = 0, tmp;    
    vector<long long> val;
    int n;
    cin >> n;
    int a = 3 * n;
    // 输入数据
    while (a--)
    {
        cin >> tmp;
        val.push_back(tmp);
    }
	// 排序
    sort(val.begin(), val.end(), greater<int>());
	// 贪心
    for (int i = 1; i < 2 * n; i += 2)
    {
        ret = ret + val[i];
    }
    cout << ret << endl;
}

---

2.删除公共字符

---

原题链接：删除公共字符

• 法一：暴力搜索

直接有几个需要删除的字符就遍历几遍源字符串，每次遍历删去一种字符，直到需要删除的字符串遍历完毕。

#include 
#include 
using namespace std;

int main()
{
    string s, sub;
    getline(cin, s);
    getline(cin, sub);
    size_t len2 = sub.size();
    for (size_t i = 0; i < len2; i++)
    {
        int j = 0;
        while (j < s.size())
        {
            if (s[j] == sub[i])
            {
                s.erase(j, 1);
            }
            else
            {
                j++;
            }
        }
    }

    cout << s << endl;
    return 0;
}

时间复杂度为 $O(n\ast m)$ ，空间复杂度为 $O(1)$ 。

• 法二：哈希表

• 将需要删除的字符串中的字符先遍历一遍，根据字符映射，在相应位置标记出现。
• 再遍历一遍源字符串，根据字符映射，在哈希表中查找。
• 如果被标记过，删除此字符；未标记过，保留此字符。

此种方法的优点是：只需要遍历一遍源字符串和删除字符串,时间复杂度降为 $O(n+m)$ 。

#include 
#include 
using namespace std;
int main()
{
    string s, sub;
    getline(cin, s);
    getline(cin, sub);
    bool jud[128] = { 0 };

    for (auto ch : sub)
    {
        jud[ch] = true;
    }
    int i = 0;
    while (i < s.size())
    {
        if (jud[s[i]])
        {
            s.erase(i, 1);
        }
        else
        {
            ++i;
        }
    }

    cout << s << endl;
    return 0;
}

---

3.排序子序列

---

原题链接：排序子序列

此题并不是一个特别难的题，但是是一个坑非常多的题，建议先来做一做这道题，再来看题解。

我先来讲一下这道题的坑。

题目难读懂

• 首先，要理解一个概念，非递增序列和非递减序列，不要小看这个概念，如果搞不清楚，后面很容易翻车。
• 非递增序列：$a[i]>=a[i+1]$ ，如：5 5 5 3 2 1 。
• 非递减序列：$a[i]<=a[i+1]$ ，如：1 1 1 2 3 4 。

边界数据容易忘判断

• 这里先给一组数据—— 5 4 3 2 1 2
• 这个数组前面都是递减数列，但是最后一个变成了一个单独的数列，有些人设置的循环结束条件是 i < n - 1，所以判断不到 a[i] >= a[i + 1] ，这个是一个常见的错误。

数组下标记错

• 这里先给一组数据—— 1 2 3 2 3
• 当判断到 1 2 3 时没有问题，当判断下一个 2 时，发现不符合非递减，但是此时跳出了循环，下标仍然指向 3 ，这时会将 3 2视为一组，接下来的 2 3 又会视为一组，多判断了1组。
• 所以，在跳出循环时，记得要将下标++。

相等数据判断出错

• 这里先给一组数据—— 2 2 2 1 1 1 1 2 2 2 1 1 1
• 这个问题可以说是最隐蔽的一个问题，如果你先判断非递减序列，满足条件，进入循环，到 1 停止，下面你要判断非递增序列，也满足条件，但是事实上，你这时多算了一组。
• 上面这组数据如果你先非递增序列，那么到下一组2停止，但是下面你要判断非递减序列，这时就又会出现多算一组的问题。
• 解决方法见下面代码。

int main()
{
    vector<int> input;
    int n;
    cin >> n;
    input.resize(n + 1);// 多开一个空间
    input[n] = 0;// 为了解决边界数据没判断的问题
    int flag = 2;// 0为非递增，1为非递减
    int tmp, cnt = 0;

    for (int i = 0; i < n; i++)
    {
        cin >> tmp;
        input[i] = tmp;
    }

    int i = 0;
    while (i < n)
    {
        // 判断非递增和非递减前，先让等于的数据走完
        while (i < n && input[i] == input[i + 1])
        {
            i++;
        }
		// 非递减
        while (i < n && input[i] <= input[i + 1])
        {
            flag = 0;
            i++;
        }
		// 当进入上面的循环时，并且循环结束时，指针+1，序列数+1
        if (flag == 0)
        {
            i++;
            cnt++;
        }
		// 判断非递增和非递减前，先让等于的数据走完
        while (i < n && input[i] == input[i + 1])
        {
            i++;
        }
		// 非递增
        while (i < n && input[i] >= input[i + 1])
        {
            flag = 1;
            i++;
        }
		// 当进入上面的循环时，并且循环结束时，指针+1，序列数+1
        if (flag == 1)
        {
            i++;
            cnt++;
        }
    }

    cout << cnt;
    return 0;
}

下面的判断条件太冗余了，我们可以先比较数据，再进入循环，这样可以优化一下逻辑。

#include 
#include 
using namespace std;

int main()
{
    vector<int> input;
    int n;
    cin >> n;
    input.resize(n + 1);
    input[n] = 0;
    int tmp, cnt = 0;

    for (int i = 0; i < n; i++)
    {
        cin >> tmp;
        input[i] = tmp;
    }

    int i = 0;
    while (i < n)
    {
        // 先判断数据大小，再进入循环
        if (input[i] > input[i + 1])
        {
            while (i < n && input[i] >= input[i + 1])
            {
                i++;
            }
            i++;
            cnt++;
        }
        else if (input[i] < input[i + 1])
        {
            while (i < n && input[i] <= input[i + 1])
            {
                i++;
            }
            i++;
            cnt++;
        }
        else
        {
            i++;
        }
    }


    cout << cnt;
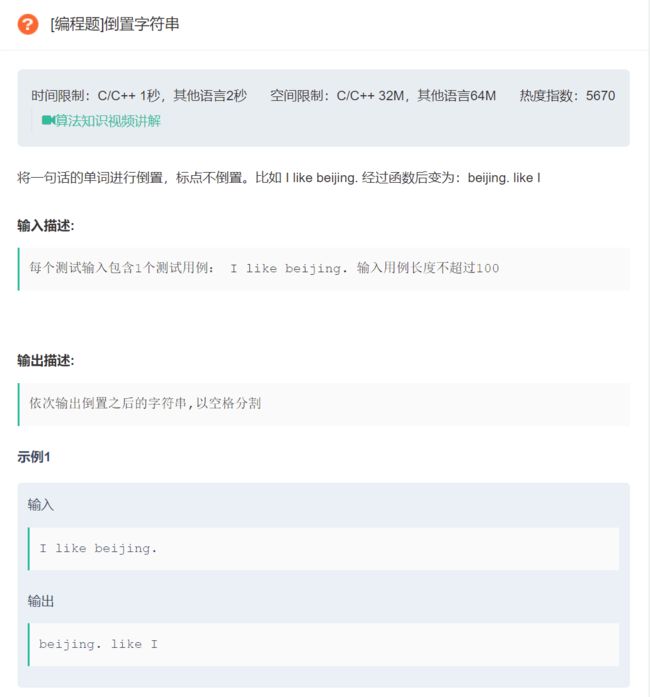
    return 0;
}

---

4.倒置字符串

---

原题链接：倒置字符串

法一：尾接法

思路：

• 直接使用vector容器一个一个接收单词，进行微调整后，将其直接反向续在空字符串上。

#include 
#include 
#include 
using namespace std;

int main()
{
    vector<string> ve;
    string ret, tmp;
	// 接收单词并进行微调整，在后面插入一个空格符
    while (cin >> tmp)
    {
        ve.push_back(tmp);
        ve.back() += " ";
    }

    auto rbegin = ve.rbegin(), rend = ve.rend();
	// 反向插入
    while (rbegin != rend)
    {
        ret += *rbegin;
        rbegin++;
    }
	// 删除最后一个空格
    ret.pop_back();

    cout << ret << endl;
    return 0;
}

法二：暴力翻转法

• 首先，直接反转字符串。
• 其次，对于单词再依次进行反转。

#include 
#include 
#include 
using namespace std;

int main()
{
    string ret;
    getline(cin, ret);
    reverse(ret.begin(), ret.end());

    auto cur = ret.begin();
    size_t cur_pos = 0;
    // 查找空格，每找到一个空格进行一次反转
    size_t pos = ret.find(" ", cur_pos);
    
    while (pos != -1)
    {
        if (pos != -1)
        {
            reverse(cur, cur + pos - cur_pos);
            cur += pos - cur_pos + 1;
            cur_pos += pos - cur_pos + 1;
        }
        pos = ret.find(" ", cur_pos);
    }
    // 反转最后一个单词
    reverse(cur, ret.end());
	
    cout << ret << endl;
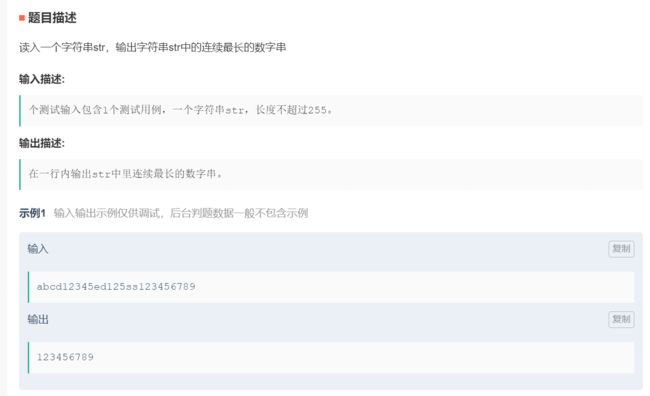
    return 0;
}

---

⛏5.字符串中连续最长的数字串

---

原题链接：在字符串中找出连续最长的数字串

这个题的思路不难，难点就是实现上，所以直接看代码：

#include 
#include 
using namespace std;

int main()
{
    string str;
    cin >> str;
    str += 'a';// 使最后的连续字符串可以被记录
    // 如 12345 这样的字符串记为 12345a 在最后一个位置放一个字母，便于后面记录数据，不用单独判断

    size_t len = str.size();
    size_t max_len = 0, cur_len = 0;
    size_t max_pos = 0, cur_pos = 0;
    int flag = 0;// 0为不是数字串，1为是数字串
	// 遍历字符串
    for (size_t i = 0; i < len; ++i)
    {
        if (str[i] >= '0' && str[i] <= '9')
        {
            // 状态切换，记录位置
            if (flag == 0)
            {
                cur_pos = i;
            }
            flag = 1;
            cur_len++;
        }
        else
        {
            if (cur_len > max_len)
            {
                max_len = cur_len;
                max_pos = cur_pos;
            }
            // 切换状态
            flag = 0;
            cur_len = 0;
        }
    }

    for (int i = max_pos; i < max_pos + max_len; ++i)
    {
        cout << str[i];
    }
    return 0;
}

---

⚒6.数组中出现次数超过一半的数字

---

原题链接：数组中出现次数超过一半的数字

法一：哈希表

题目给出了传入数组的取值和长度，那么直接哈希就完事了，反正哈希表是定长的，遍历是常数，时间复杂度还是 $O(n)$ （bushi）。

static int cnt[10001] = { 0 };
class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int len = numbers.size();
        for (auto e : numbers)
        {
            cnt[e]++;
        }

        for (int i = 0; i < 10001; i++)
        {
            if (cnt[i] > len / 2)
            {
                return i;
            }
        }

        return -1;
    }
};

法二：同归于尽法

虽然上一个方法可以run过去，但是时间是绝对长了，不一定符合 $O(n)$ ，对上一个方法存在质疑的同学可以看这个方法。

这个数组有一个数据出现超过了数组长度的一半，并且测试用例绝对是有答案的，所以就有了同归于尽法。

• 第一个数字作为第一个士兵，守阵地；count = 1；
• 遇到相同元素，count++;
• 遇到不相同元素，即为敌人，同归于尽,count–；当遇到count为0的情况，又以新的 i 值作为守阵地的士兵，继续下去，到最后还留在阵地上的士兵，有可能是主元素。
• 再加一次循环，记录这个士兵的个数看是否大于数组一般即可。

法二来自牛客网网友的分享

具体实现：

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cnt = 0;
        size_t len = numbers.size();
        // 选择第一个数字当士兵
        int num = numbers[0];
        if (len == 1)
        {
            return numbers[0];
        }

        for (int i = 0; i < len; ++i)
        {
            // cnt==0，换士兵
            if (cnt == 0)
            {
                num = numbers[i];
            }
            
            if (numbers[i] == num)
            {
                ++cnt;
            }
            else
            {
                --cnt;
            }
        }

        return num;
    }
};

---

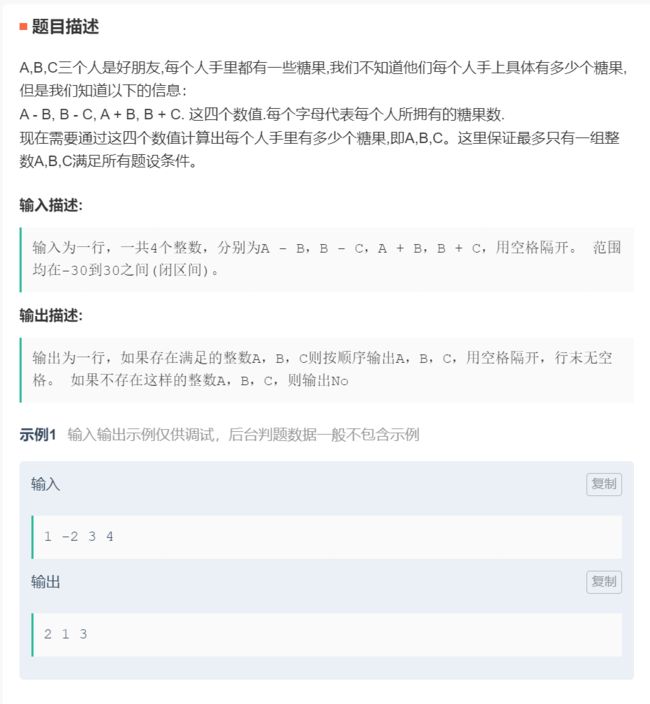
7.计算糖果

---

原题链接：计算糖果

这道题没有什么难度，就是解三元一次方程，最后逆回去检查一下结果是否为整数即可。

#include 
using namespace std;

int main()
{
    int a, b, c, d;
    cin >> a >> b >> c >> d;
    int A, B, C;

    A = (a + c) / 2;
    B = (b + d) / 2;
    C = d - B;

    if (A - B != a || B - C != b || A + B != c || B + C != d)
    {
        cout << "No";
        return 0;
    }

    cout << A << " " << B << " " << C;
    return 0;
}

---

8.进制转换

---

原题链接：进制转换

我们先了解一下N进制的本质：
假设N进制每个位置上的数是 $a_i$ 则一个4位的N进制数可以表示为：

则这个数字的数值 =

例：10进制数178可以表示为：

16进制数1AB可以表示为：

然后我们再继续思考一下：如何获得一个十进制的每一位？比如：对于十进制数178，我们想要获得1、7、8，先用178对10取模，可以获得个位数8，然后将178除10，然后再对10去摸摸，可以获得10位数7…
所以，只要每次对数字取模10然后除10，就可以获得数字的每一位了，同理，对于N进制的数字来说，只要每次对数字取模N然后除N，就可以获得N进制的每一位了。

注：注意题目中说M是32位整数，所以有可能是负数和0，如果是0的话直接返回，如果是负数，就先转化成正数，最后再加上符号位;如果是正数，就让M一直取余N和除N。

以上思路取自于牛客网网友——王清楚

class Solution {
public:
    /**
     * 进制转换
     * @param M int整型 给定整数
     * @param N int整型 转换到的进制
     * @return string字符串
     */
    string solve(int M, int N) {
        string s = "0123456789ABCDEF";
        string ret;
        if (M == 0)
        {
            cout << "0";
            return 0;
        }
        int tmp = M < 0 ? -M : M;


        while (tmp)
        {
            ret += s[tmp % N];
            tmp /= N;
        }

        if (M < 0)
            ret += '-';

        reverse(ret.begin(), ret.end());
        return ret;
    }
};

---

9.统计回文

---

原题链接：统计回文

暴力插入法

思路非常简单，在A串的各个位置插入B串，再判断A串是否为回文，最后统计回文的个数即可。

#include 
#include 
using namespace std;

bool is_pal(string a, string& b, int pos)
{
    // 将a，b传过来再合并，由于b不变，所以直接传引用减少拷贝
    int i = 0, j;
    a.insert(pos, b);
    j = a.size() - 1;
	// 判断是否为回文
    while (i < j)
    {
        if (a[i] != a[j])
            return false;
        i++;
        j--;
    }

    return true;
}

int main()
{
    string a, b;
    cin >> a >> b;
    int cnt = 0;
	// 在a的各个位置插入b，记录满足回文的数量
    for (int i = 0; i <= a.size(); ++i)
    {
        bool bl = is_pal(a, b, i);
        if (bl == true)
            cnt++;
    }

    cout << cnt << endl;
    return 0;
}

---

10.连续最大和

---

原题链接：连续最大和

这是一道非常经典的动态规划问题：

• 状态：$f(x)$ —— 从上一段连续的最大和到 x 位置的最大和

• 状态转移方程：$f(x)=max(f(x-1)+a[x],a[x])$ —— 如果上一段的连续最大和与当前数的和大于当前数，就取上一段的连续最大和与当前数的和，反之，取当前数（相当于如果 前面连续串的和的最大值 以及 当前数 相加的和 如果还不如当前数，不如从这一位置重新开始一个连续的子串，反之继续延续前面的连续串）

• 初始值：$f(0)=a[0]$ —— 从a[0]开始子串

• 结果：从 $f(0)-f(n-1)$ 中选出最大值。因为连续串不确定，所以最后要判断一下。

• 实例：$-2,1,-3,4,-1,2,1,-5$

• 序号	0	1	2	3	4	5	6	7
  $a[x]$	-2	1	-3	4	-1	2	1	-5
  $f(x)$	-2	1	-2	4	3	5	6	1

再来形象总结一下连续串的思路：

相当于你有一个大型的家族，如果前面你家族的资产很丰厚，和你的资产加起来超过了你原本的资产（你可能还欠钱了），那么你选择继承家产；但是如果你家道中落，家里欠了钱，那么你就可以选择自己出去单干，不要被家族牵连，你又开始建立了一个新家族。你的子孙以你为榜样，继续上面的过程。

最后你的后代翻阅族谱，要找到祖上最阔器的时代，于是将一代代人的资产比较，得到祖上最阔的一代的资产。

代码实现：

#include 
#include 
using namespace std;

int main()
{
	vector<int> v1;
	int n, tmp;
	cin >> n;

	
	for (int i = 0; i < n; ++i)
	{
		cin >> tmp;
		v1.push_back(tmp);
	}

	int Max = v1[0];

	for (int i = 1; i < n; ++i)
	{
		v1[i] = max(v1[i] + v1[i - 1], v1[i]);
		Max = max(v1[i], Max);
	}

	cout << Max << endl;

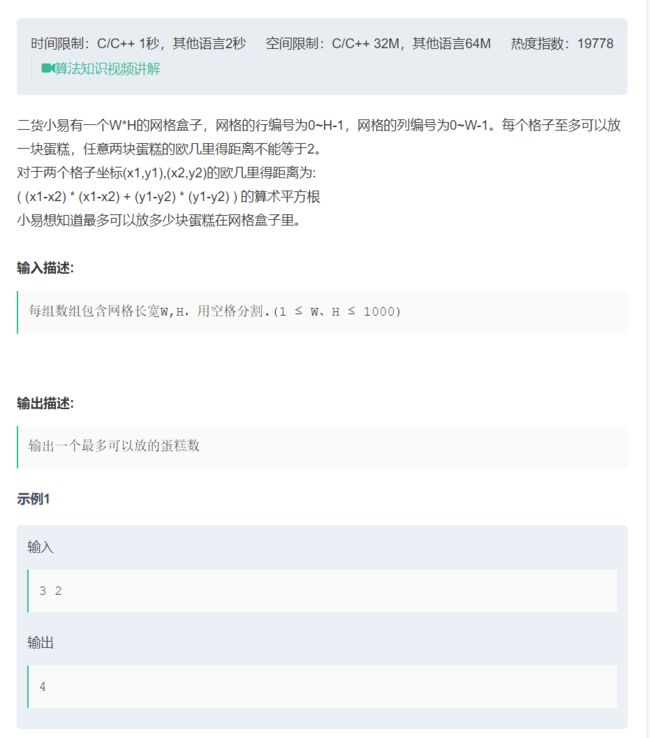
	return 0;
}

---

⚙11.不要二

---

原题链接：不要二

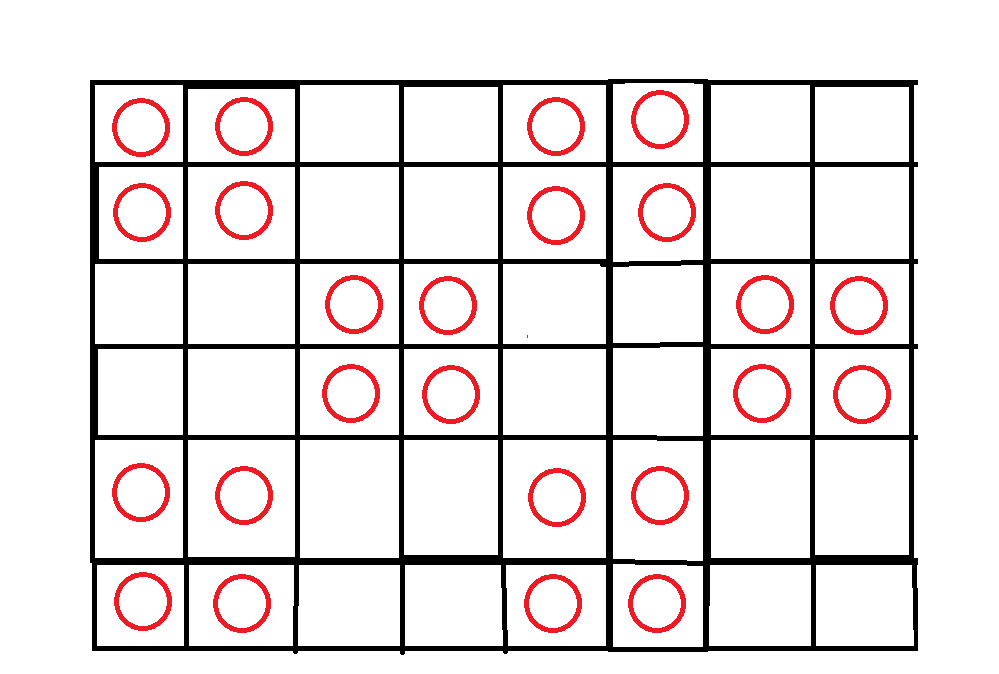
这个题就是一个贪心算法的题目，直接从最左上角的格子开始放蛋糕就可以。

别看题目给的定义很复杂，但是其实意思就是在放置蛋糕的格子的上下左右距离蛋糕2格的地方不能有蛋糕。

理想贪心状态下，所得的蛋糕格是这样的：

据观察，蛋糕是以4为单位周期出现的。

法一：贪心暴力求解

• 首先，创建一个大小为m*n的数组，初始化值为0，0意味着没有蛋糕。
• 从左上角开始放一个蛋糕，记为1。
• 依次遍历数组每一格，符合条件就放一个蛋糕，同时++蛋糕数量，不符合直接跳过。
• 最后，输出蛋糕数量即可

#include 
#include 
using namespace std;

int main()
{
    int m, n;
    cin >> m >> n;
    int cnt = 0;
    vector<vector<int>> ret(m, vector<int>(n));
    // 数组为一行或者一列时，需要特别判断
    if (m == 1)
    {
        // 当为一行时，先算有几个四列组
        int tmp = n / 4;
        // 再算余下来的列
        int reu = n % 4;
        // 蛋糕数 = 四列组数*2 + 余下列的蛋糕数
        cnt += 2 * tmp;
        cnt += reu >= 2 : 2 ? 1;
        cout << cnt << endl;
    }
    else if (n == 1)
    {
        // 同理
        int tmp = m / 4;
        int reu = m % 4;
        cnt += 2 * tmp;
        cnt += reu >= 2 : 2 ? 1;;
        cout << cnt << endl;
    }

    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (i < 2 && j < 2)
            {
                // 左上的四个蛋糕单独判断
                ret[i][j] = 1;
                cnt++;
            }
            else if (i < 2)
            {
                // 前两行单独判断
                if (ret[i][j] == 0 && ret[i][j - 2] == 0)
                {
                    ret[i][j] = 1;
                    cnt++;
                }
            }
            else if (j < 2)
            {
                // 前两列单独判断
                if (ret[i][j] == 0 && ret[i - 2][j] == 0)
                {
                    ret[i][j] = 1;
                    cnt++;
                }
            }
            else
            {
                // 其余情况
                if (ret[i][j] == 0 && ret[i - 2][j] == 0 && ret[i][j - 2] == 0)
                {
                    ret[i][j] = 1;
                    cnt++;
                }
            }
        }

    }

    cout << cnt << endl;
    return 0;
}

以上写法太冗余，所以我们可以进行优化，反向思维，直接将不能放蛋糕的地方置为1，这样代码会好处理很多。

#include 
using namespace std;

int main()
{
    int m, n;
    cin >> m >> n;
    int cnt = 0;
    vector<vector<int>> ret(m, vector<int>(n));

    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            // 当可以放蛋糕时
            if (ret[i][j] == 0)
            {
                cnt++;
				// 将此位置限制不能放蛋糕的位置置为1
                if (i + 2 < m)
                    ret[i + 2][j] = 1;
                if (j + 2 < n)
                    ret[i][j + 2] = 1;
            }
        }
    }

    cout << cnt << endl;
    return 0;
}

时间复杂度 $O(m\ast n)$ ，空间复杂度 $O(m\ast n)$ 。

法二：公式法

此方法灵感来自牛客网网友：

#include 
using namespace std;

int main()
{
    int m, n;
    cin >> m >> n;

    int oddLineSum = (n / 4) * 2 + (n % 4 >= 2 ? 2 : n % 4);
    int evenLineSum = ((n - 2) / 4) * 2 + ((n - 2) % 4 >= 2 ? 2 : (n - 2) % 4);
    int ret = (m / 4) * (oddLineSum + evenLineSum) * 2;

    int remLine1 = m % 4 == 1 ? oddLineSum : 0;
    int remLine2 = m % 4 == 2 ? oddLineSum * 2 : 0;
    int remLine3 = m % 4 == 3 ? oddLineSum * 2 + evenLineSum : 0;

    ret += remLine1 + remLine2 + remLine3;
    cout << ret << endl;
    return 0;
}

时间复杂度 $O(1)$ ，空间复杂度 $O(1)$ 。

---

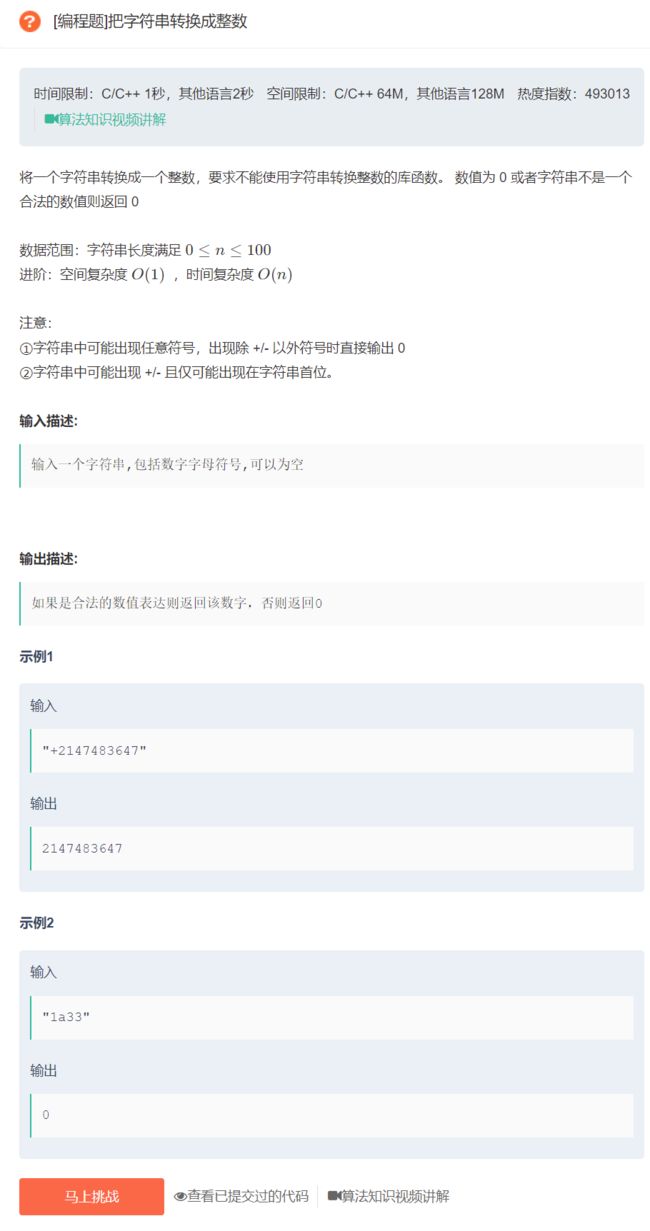
12.把字符串转换成整数

---

原题链接：把字符串转换成整数

具体思路：

• 首先，判断第一位是否为符号位，如果为符号位，分开判断正负即可；如果为数字位，记录数字；如果为其他符号，直接返回0。
• 其次，对后面的字符一一进行判断。如果为数字，将之前的数字*10 再加上这一位的数字即可；如果为其他符号，那么直接返回0；
• 最后，注意符号，返回结果即可。

class Solution {
public:
    int StrToInt(string str)
    {
        // 特殊判断
        if (str.empty())
            return 0;
        if (str.size() == 1)
        {
            if (str[0] >= '0' && str[0] <= '9')
            {
                return str[0];
            }
            else
            {
                return 0;
            }
        }
        // flag记录数字正负，num记录字符串转换的数字
        int flag = 1, num = 0;
        int len = str.size();
        // 判断第一个字符
        if (str[0] == '+')
            flag = 1;
        else if (str[0] == '-')
            flag = -1;
        else if (str[0] >= '0' && str[0] <= '9')
            num += str[0] - '0';
        else
        {
            cout << 0 << endl;
            return 0;
        }
		
        // 依次判断
        for (int i = 1; i < len; ++i)
        {
            if (str[i] >= '0' && str[i] <= '9')
            {
                num = num * 10 + str[i] - '0';
            }
            else
            {
                return 0;
            }
        }
		// 返回num*flag
        return num * flag;
    }
};

代码还是有点长，我们可以优化一下：

class Solution {
public:
    int StrToInt(string str) {
        int flag = 1;
        int ret = 0;

        if (str[0] == '+')
            flag = 1;
        else if (str[0] == '-')
            flag = -1;


        for (int i = str[0] == '+' || str[0] == '-' ? 1 : 0; i < str.size(); ++i)
        {
            // C库中提供的判断一个字符是否为数字字符的函数
            if (isdigit(str[i]))
            {
                ret = ret * 10 + str[i] - '0';
            }
            else
                return 0;
        }

        return ret * flag;
    }
};

---

后记

---

恭喜你，已经迈出了成功的第一步。

这个是一个新的系列——《经典笔试编程题》，隶属于【刷题日记】系列，白晨开这个系列的目的是向大家分享经典的笔试编程题，以便于大家参考，查漏补缺以及提高代码能力。如果你喜欢这个系列的话，不如关注白晨，更快看到更新呀。

本文是经典笔试编程题的第一篇，后续会加入更多类型的笔试题，包括数据结构，算法等，难度也会相应提高✈。

---

如果解析有不对之处还请指正，我会尽快修改，多谢大家的包容。

如果大家喜欢这个系列，还请大家多多支持啦！

如果这篇文章有帮到你，还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧！喜欢白晨【算法】系列的话，不如关注白晨，以便看到最新更新哟！！！

我是不太能熬夜的白晨，我们下篇文章见。