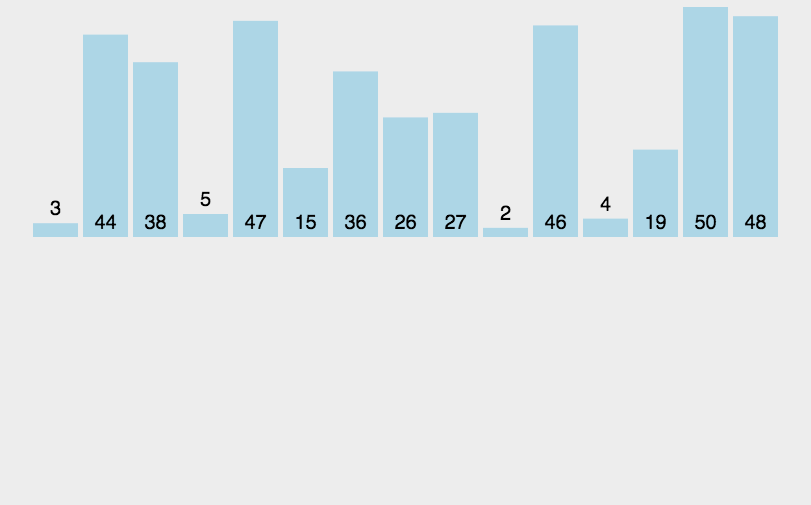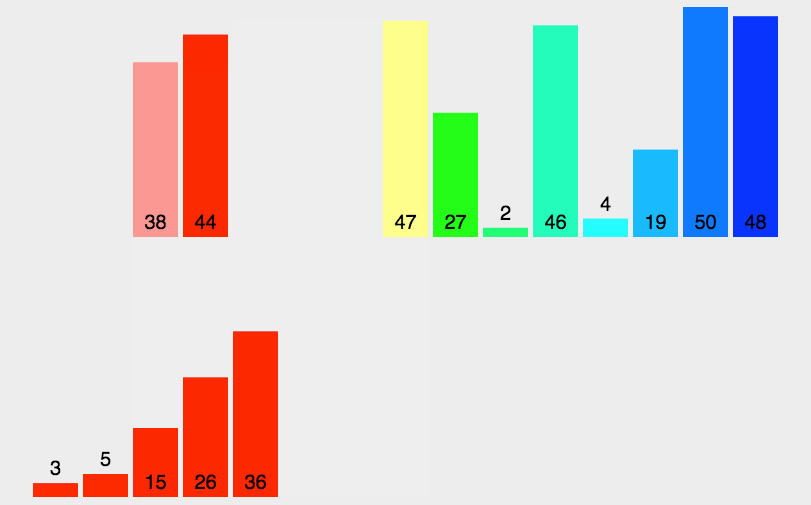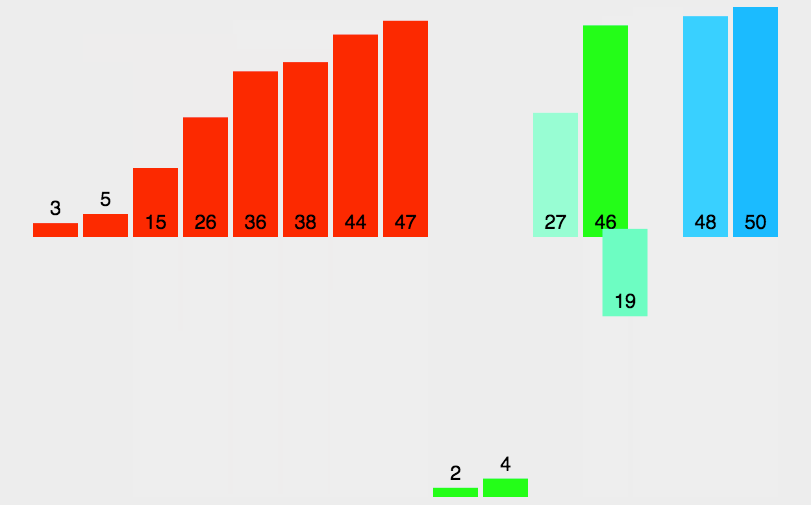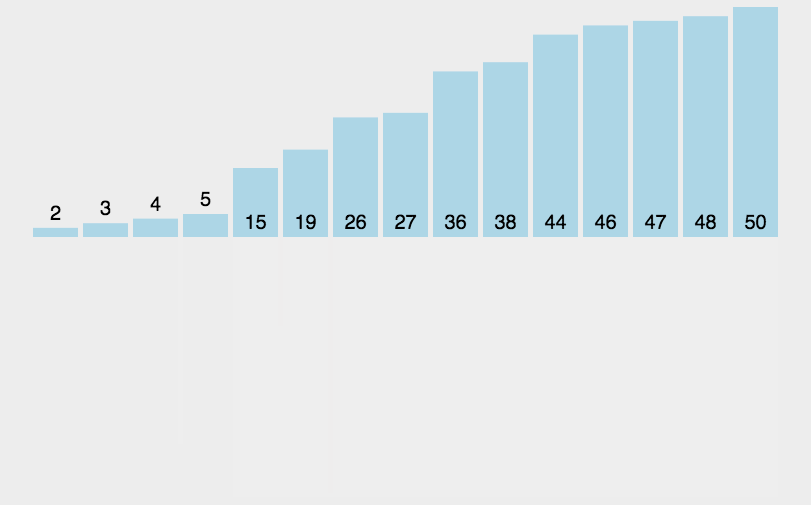
手撕八大排序
排序算法
- 1.直接插入排序
- 2.希尔排序
- 3.选择排序
- 4.堆排
- 5.冒泡排序
- 6.快速排序
-
- 单趟排序—挖坑法
- 前后指针法
- 排序的非递归
- 7.归并排序
-
- 归并递归
- 非递归
- 8.统计排序
- 稳定性
1.直接插入排序
步骤一:单次排序,将x插入[0,end]的有序区间。
int end ;
int x ;
//单趟排序,理解为把x插入[0,end]的有序区间
while (end >= 0)//注意end的边界
{
if (a[end] > x)
{
a[end + 1] = a[end];
end--;//end为0时--,end就等于-1,a[0]的就等于x
}
else
{
break;
}
}
a[end + 1] = x;//有两种情况,1.end<0了 2.x的值比end大
end的两个结束条件:
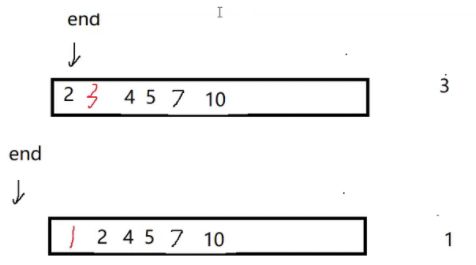
步骤二:实现整个数组的排序
从下标角度来说,如果有n个数
end的取值范围[0,n-2]因为最后一个数的下标为n-1,end最终落的位置就是n-2,x=a[end+1];
//时间复杂度为O(n^2)
//空间复杂度为0(1)
void Insertsort(int* a, int n)
{
assert(a);
int i = 0;
for (i = 0; i < n-1; i++)
{
int end = i ;
//end作为下标最终会变成n-2
//(最后一个数的下标为n-1,倒数第二个数的下标为n-2)
int x = a[end + 1];
//单趟排序,理解为把x插入[0,end]的有序区间
while (end >= 0)
{
if (a[end] > x)
{
a[end + 1] = a[end];
end--;//end为0时--,end就等于-1,a[0]的就等于x
}
else
{
break;
}
}
a[end + 1] = x;//有两种情况,1.end<0了 2.x的值比end大
}
}
2.希尔排序
//单趟插入预排序
int gap = 3;
int end;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = x;
//两种情况:1.end为负数 2.a[end]<=x,break跳出循环
步骤二:把数组分成了gap组,每组排序
int gap = 3;
for (int i = 0; i < n - gap; i += gap)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = x;
}
}
int gap=3;
for (int j = 0; j < gap; j++)
//分成了gap组
//第一组下标从0开始
//第二组下标从1开始
//第三组下标从2开始
//以此确定i的开始位置
{
for (int i = j; i < n - gap; i += gap)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = x;
}
}
}
步骤三优化:多组一锅炖
for (int i = 0; i < n - gap; i++)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = x;
}
}
最终步骤:控制gap
int gap = n;
while (gap>1)
{
gap = gap / 3+1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
a[end + gap] = x;
}
}
}
3.选择排序
选出最小值和最大值的下标
void SelectSort(int* a, int n)
{
int end = n - 1;
int begin = 0;
while (begin < end)
{
int mini = begin;
int max = begin;
for (int i = 0; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;//如果a[i] < a[mini],就记录mini的值,也就是最小值的下标
}
if (a[i] > a[max])
{
max = i;//如果a[i] >a[mini],就记录max的值,也就是最大值的下标
}
}
//选出[begin,end]区间的最大最小值,然后交换
//最小值放到第一位,最大值放到最后
Swap(&a[begin], &a[mini]);
Swap(&a[end], &a[max]);
//缩小区间
begin++;
end--;
}
}
但是这里有错误


当第一个数是最大值时,第一个数和最小的数交换,max也被换了,所以要修正
void SelectSort(int* a, int n)
{
int end = n - 1;
int begin = 0;
while (begin < end)
{
int mini = begin;
int max = begin;
for (int i = 0; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;//如果a[i] < a[mini],就记录mini的值,也就是最小值的下标
}
if (a[i] > a[max])
{
max = i;//如果a[i] >a[mini],就记录max的值,也就是最大值的下标
}
}
//选出[begin,end]区间的最大最小值,然后交换
//最小值放到第一位,最大值放到最后
Swap(&a[begin], &a[mini]);
if (begin == max)//当begin==max,最大的数被换走,要修正max位置
{
max = mini;
}
Swap(&a[end], &a[max]);
//缩小区间
begin++;
end--;
}
}
4.堆排
建立一个小堆,比它大就往下调
void PrintTopK(int* a, int n, int k)
{
HP hp;
HeapInit(&hp);
for (int i = 0; i < k; i++)
{
HeapPush(&hp, a[i]);
}
for (int i = k; i < n; i++)
{
if (a[i] >HeapTop(&hp))
{
HeapPop(&hp);
HeapPush(&hp, a[i]);
}
}
HeapPrint(&hp);
HeapDestroy(&hp);
}
5.冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (int j = 0; j < n; j++)
{
for (int i = 0; i < n - 1 - j; i++)
//先单趟排序,让最大的数到最后一个位置
//注意好i的边界
{
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
}
}
}
}
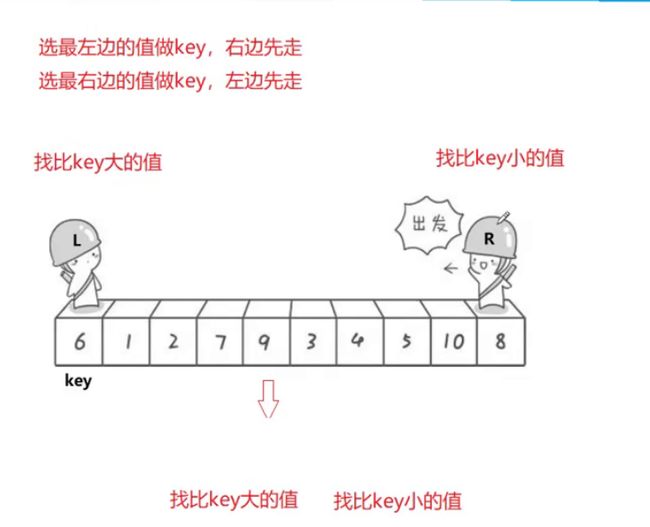
6.快速排序
当右边作为key时
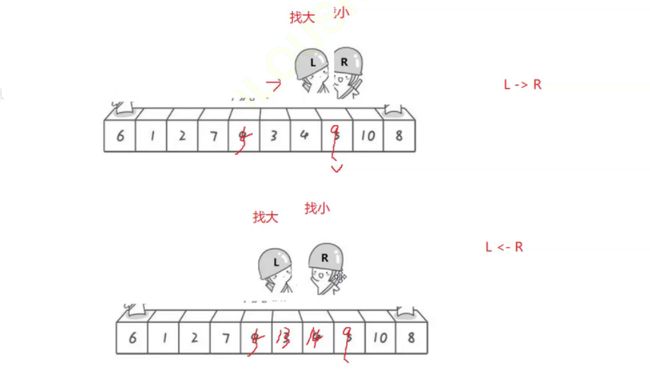
右边作为key,相遇前的最后一轮会发生两种情况:
1.L撞到R
L在找比key大的数,在R的位置相遇
2.R撞到L
L找到比key大的数停下来,R在找比key小的数,R找不到就会在L的位置相遇
| 接下来就是代码的实现 |
int Partion(int* a, int left, int right)
{
int key = left;//最左边作为key
while (left < right)
{
while (a[right] > a[key])//右边先走,找到比key小的就停下
{
right--;
}
while (a[left] < a[key])//左边再走,找到比key大的就停下
{
left++;
}
Swap(a[left], a[right]);//交换
}
Swap(a[left], a[key]);//最后把key和相遇点交换
return left;
}
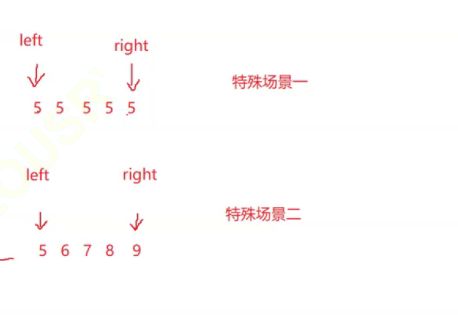
| 这里还有两种情况会导致错误 |
场景一:a[right]不比a[key]大 且 a[left] 不比 a[key]小,left永远小于right,造成死循环
场景二:有序,right会一直走直到到达left的位置停下,left在去找比key大的数,left和right会错开
| 所以进一步优化 |
int Partion(int* a, int left, int right)//单趟排完,比key小的到key左边,比key大的到右边
{
int key = left;//最左边作为key
while (left < right)
{
while (a[right] >= a[key]&&left<right)//右边先走,找到比key小的就停下
{
right--;
}
while (a[left] <= a[key]&&left<right)//左边再走,找到比key大的就停下
{
left++;
}
Swap(&a[left], &a[right]);//交换
}
Swap(&a[left], &a[key]);//最后把key和相遇点交换
return left;
}
left
int Partion(int* a, int left, int right)//单趟排完,比key小的到key左边,比key大的到右边
{
int key = left;//最左边作为key
while (left < right)
{
while (a[right] >= a[key]&&left<right)//右边先走,找到比key小的就停下
{
right--;
}
while (a[left] <= a[key]&&left<right)//左边再走,找到比key大的就停下
{
left++;
}
Swap(&a[left], &a[right]);//交换
}
Swap(&a[left], &a[key]);//最后把key和相遇点交换
return left;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)//等于就是只有一个值,大于就是区间不存在
{
return;
}
int key = Partion(a,left,right);
QuickSort(a, left, key-1);
QuickSort(a, key+1, right);
}
| 面对有序三数取中(补其缺陷)/完整代码 |
int GetMidIndex(int* a, int left, int right)
{
int mid = (right + left);
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
int Partion(int* a, int left, int right)//单趟排完,比key小的到key左边,比key大的到右边
{
//三数取中
int mini = GetMidIndex(a, left, right);
//int key = left;//最左边作为key
Swap(&a[left], &a[mini]);
int key = left;
while (left < right)
{
while (a[right] >= a[key]&&left<right)//右边先走,找到比key小的就停下
{
right--;
}
while (a[left] <= a[key]&&left<right)//左边再走,找到比key大的就停下
{
left++;
}
Swap(&a[left], &a[right]);//交换
}
Swap(&a[left], &a[key]);//最后把key和相遇点交换
return left;
}
单趟排序—挖坑法
int Partion2(int* a, int left, int right)
{
int mini = GetMidIndex(a, left, right);
Swap(&a[left], &a[mini]);
int key = a[left];
int pivot = left;
while (left < right)
{
while (left < right && a[right] >= key)//右边找小,放到左边的坑里
{
right--;
}
a[pivot] = a[right];
pivot = right;
while (left < right && a[left] <= key)//左边找大,放到右边的坑里
{
left++;
}
a[pivot] = a[left];
pivot = left;
}
a[pivot] = key;
return pivot;
}
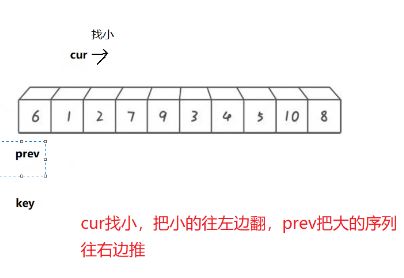
前后指针法
int Partion3(int* a, int left, int right)
{
int prev =left;
int key = left;
int cur = prev + 1;
while (cur<=right)
{
while (a[cur] >= a[key]&&cur<=right)
{
cur++;
}
if (cur <= right)
{
prev++;
Swap(&a[prev], &a[cur]);
cur++;
}
}
Swap(&a[key], &a[prev]);
return prev;
}
排序的非递归
用栈来实现
void QuickSortNonR(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, left);//插入的是值的下标,而不是值本身
StackPush(&st, right);
while (!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int key = Partion3(a, begin,end );
//分成[begin,key-1]和[key+1,end]
if (key+1 <end )//先进后出,所以先处理右边的
{
StackPush(&st, key+1);
StackPush(&st, end);
}
if (key-1 > begin)
{
StackPush(&st, begin);
StackPush(&st, key-1);
}
}
StackDestroy(&st);
}
| 栈帧上调用递归,非递归用栈(malloc)也就是堆,堆的空间大,栈帧大约8mb,递归深度太深的程序只能考虑改非递归 |
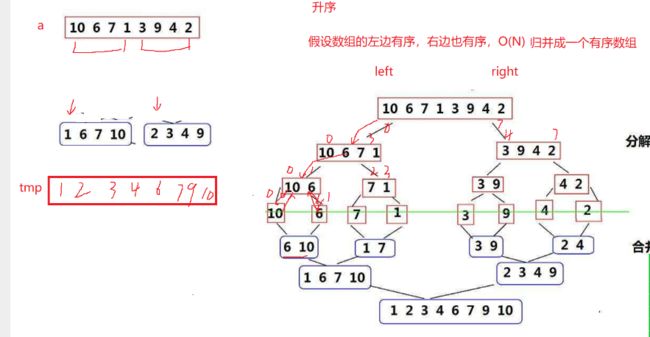
7.归并排序
归并递归
| 假设数组的左边有序,右边也有序,把左右两边归并成有序数组(递归) |
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//[left,mid],[mid+1,right]有序
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
//归并[begin1,end1]和[begin2,end2]
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i] = a[begin1];
i++;
begin1++;
}
else
{
tmp[i] = a[begin2];
i++;
begin2++;
}
}
while (begin1 <= end1)
{
tmp[i] = a[begin1];
i++;
begin1++;
}
while (begin2 <= end2)
{
tmp[i] = a[begin2];
i++;
begin2++;
}
//tmp数组拷贝到a数组
int j= 0;
for (j = 0; j <= end2; j++)
{
a[j] = tmp[j];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
非递归
| (数据为2的次方) |
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail");
exit(-1);
}
int gap= 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//[i,i+gap-1][i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int index = i;
while (begin1<=end1 && begin2<=end2)
{
if (a[begin1] <a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
for (int j = 0; j < n; j++)//像二叉树的层序遍历
{
a[j] = tmp[j];
}
gap =2*gap;
}
free(tmp);
tmp = NULL;
}
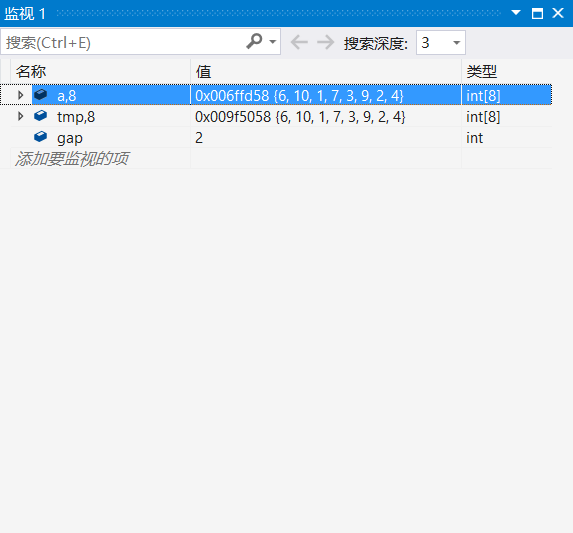
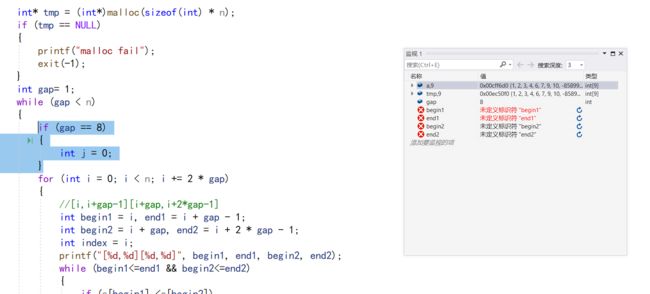
当数据个数不为2的次方时就会发生越界
如果我们想看gap等于几时,数组的情况
可以添加条件断点
if (gap == 8)
{
int j = 0;
}
//end1一越界,[begin2,end2]不存在
if (end1 >= n)
{
end1 = n - 1;
}
//[begin1,end1]存在,[begin2,end2]不存在
if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
//end2越界
if (end2 >= n)
{
end2 = n - 1;
}
| 我们也可以归并一段就返回去,这样end1和begin2越界则不需要修正,end2越界则需要修正 |
if (end1 >= n || begin2 >= n)
{
break;
}
当end2越界就需要修正:
if(end2>=n)
{
end2 = n - 1;
}
最后归并一段就返给数组a
优化完代码
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//[i,i+gap-1][i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//end1和begin2越界则不需要修正
if (end1 >= n || begin2 >= n)
{
break;
}
//end2越界则需要修正
if(end2>=n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//begin1++了所以从i的位置开始
for (int j = i; j < end2; j++)
{
a[j] = tmp[j];
}
}
gap = 2 * gap;
}
free(tmp);
tmp = NULL;
}
| 核心思想:end1,begin2,end2都有可能越界 end1和begin2越界不需要归并,end2越界则要修正 |
8.统计排序
思路:1. 统计数据出现的次数 2.根据统计
void CountSort(int* a, int n)
{
int max = a[0], min = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] <min)
{
min = a[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
printf("malloc fail");
exit(-1);
}
memset(count, 0, sizeof(int) * range);//把count数组所有值设为0
//统计次数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//根据次数排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i])
{
a[j++] = i + min;
count[i]--;
}
}
free(count);
count = NULL;
}
| 各大排序的时间复杂度 |
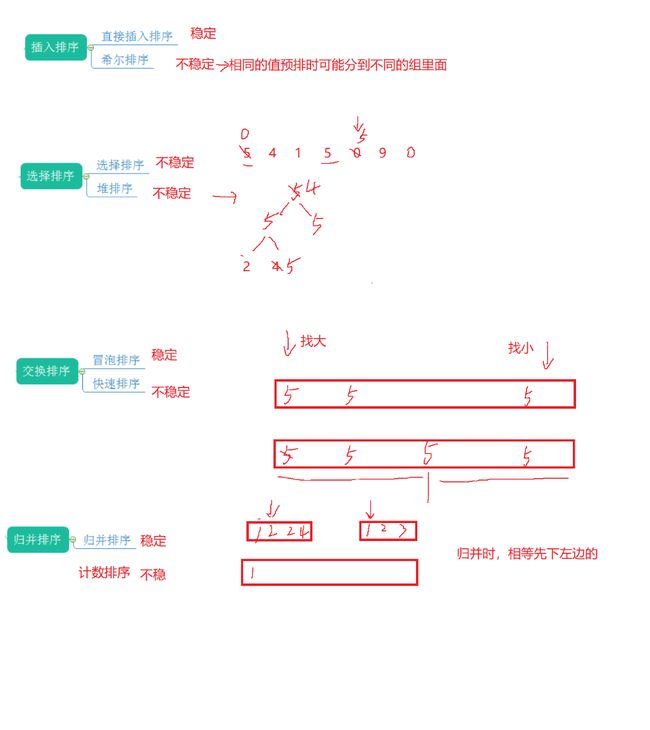
稳定性
| 稳定性的定义:数组中相同的值,在排序以后相对位置是否变化,可能会变就是不稳定,能保证不变就是稳定 |