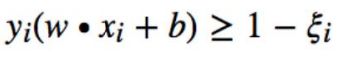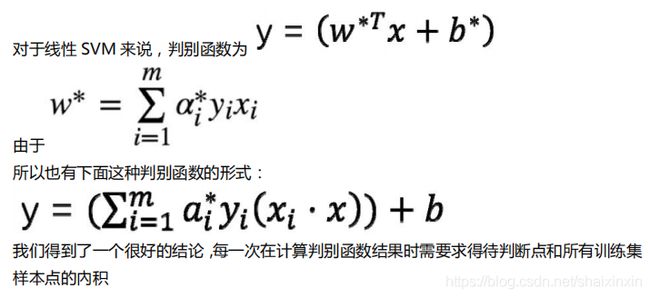SVM支持向量机
目录
-
- 一、SVM与感知机关系
-
- 1.1、SVM概念
- 1.2、感知机
- 1.3、SVM与感知机比较
- 二、几何距离与函数距离
-
- 2.1、概念
- 2.2、关键词说明
- 三、损失函数推导
- 四、最优化问题
-
- 4.1、硬间隔SVM
-
- 4.1.1、求解流程
- 4.1.2、思路推导流程
-
- 4.1.2.1、函数最优化问题（无约束条件）
- 4.1.2.2、函数最优化问题（有约束条件）
- 4.1.2.3、原始最优化问题
- 4.1.2.4、拉格朗日函数
- 4.1.2.5、对偶问题
- 4.1.2.6、KKT条件求解
- 4.1.2.7、求解SVM最优化问题
-
- 4.1.2.7.1、整体流程
- 4.1.2.7.2、先求极小值（KKT条件）
- 4.1.2.7.3、再求极大值（将极小结果反代回公式）
- 4.1.2.7.4、整理对偶函数
- 4.1.2.7.5、求得最终超平面
- 4.2、软间隔SVM
-
- 4.2.1、硬间隔SVM面临的问题
- 4.2.2、如何解决上述问题
- 4.2.3、目标函数优化
- 4.2.4、软间隔支持向量分析
- 4.2.5、软间隔最大化算法
- 4.2.6、判别函数的另一种表达形式
- 4.3、非线性SVM与核函数
-
- 4.3.1、如何处理线性不可分问题
-
- 4.3.1.1、升维
- 4.3.1.2、核函数
- 4.3.2、svm算法求解流程
一、SVM与感知机关系
1.1、SVM概念
1）SVM（Support Vector Mechine）支持向量机，是一个二分类算法，其对感知机进行了扩展，支持线性分类和非线性分类；
2）可以用于回归任务（SVR）中；也可以用于多分类中，升维方式（OvR、OvO）;
1.2、感知机
1）思想：在任意空间中找到一个超平面，将所有二分类别分割开；
2）前提：数据是线性可分的
3）模型/判别式：样本代入模型计算结果大于0则为正确分类，反正则为错误分类
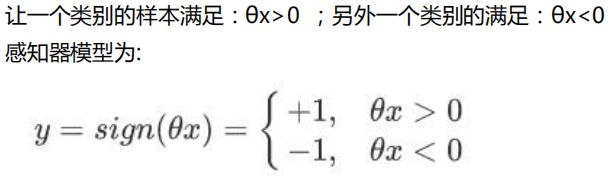
4）损失函数：期望使分类错误的所有样本到超平面的距离之和最小；（结果为0时成为完美分类器，意味着每一分错的样本）
1.3、SVM与感知机比较
1）相同点：都是寻找一个超平面解决二分类问题的算法，一侧计算结果为正则正例，一侧计算结果为负则负例；
2）不同点：损失函数不同，感知机是通过判断错的点寻找超平面；SVM是通过支持向量寻找超平面；逻辑回归通过最大似然寻找超平面；
3）高级点：SVM尝试找到一个决策边界，距离两个类别最近的样本点最远，这样模型的容忍度会更好；
二、几何距离与函数距离
2.1、概念
感知机使用几何距离计算中的损失函数大小；SVM使用函数距离；
上面为某点到平面的几何距离
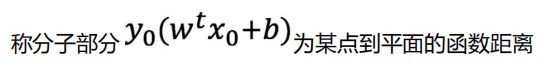
2.2、关键词说明
1）三种支持向量机：线性可分支持向量机（硬间隔最大化）、线性支持向量机（软间隔最大化）、非线性支持向量机（升维【核函数】）
2）线性可分（Linearly Separable）：即指在数据集中，可以找到一个超平面将两组数据分开
3）线性不可分（Linearly Inseparable）:即指在数据集中，无法可以找到一个超平面将两组数据分开
4）间隔（Margin）：数据点到分割超平面的距离
5）分割超平面（Separating Hyperplane）：将数据集分割开的直线或平面
6）支持向量（Support Vector）：离分割超平面最近的点
三、损失函数推导
通过线性可分支持向量机进行说明
1）实现硬间隔最大化，需要满足两个条件：能够完美分类正负例、距离最近的点越远越好
2）怎么确定超平面
3）目标：能够正确分类的平面中，距离越近的越远越好；（即找到一组最好的w和b固定一个超平面，可以完美分类正负例，且距离最近的点间隔最大）
4）转为为有约束的函数最优化问题
5）目标简化：一个超平面对应无数组w和b，只要找到其中任意一组即可，所以令函数距离等于1，则最优化问题可以简化为如下
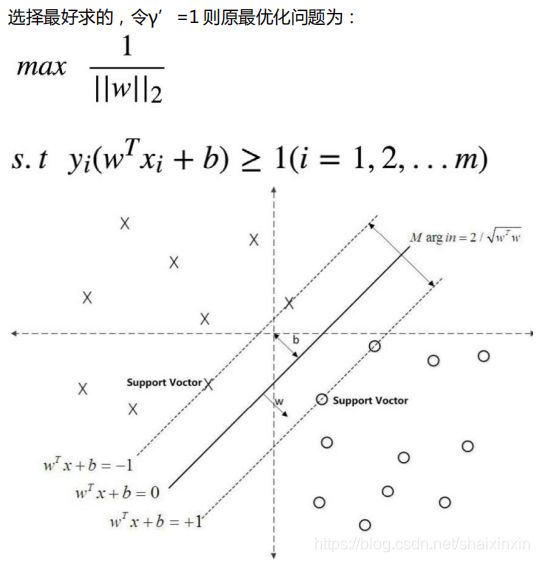
6）将求解最大问题转为最小问题，得到等价的、带约束的损失函数（s.t即约束条件，1/2后面跟的就是L2正则项）
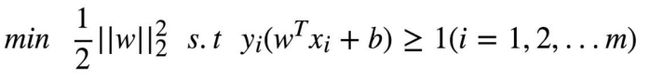
两种最优化问题求解方案：上面的损失函数+SMO、hinge Loss+GD
四、最优化问题
拉格朗日函数，将带有约束问题，对原始问题求最小，转为无约束条件，先对原始问题求最大，再求最小；
好处：去掉约束条件；
代价：一次优化变成了二次优化、每个阿尔法需要大于等于0
4.1、硬间隔SVM
4.1.1、求解流程
1）原始目标：求得一组w和b使得间隔margin最大
2）转换目标：通过拉格朗日函数，构造出目标函数，问题由求得n个w和1个b转换为求得m个α
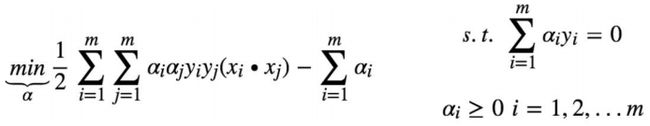
3）利用smo算法求得m个α
4）利用求得的m个α*，求得w**和b*
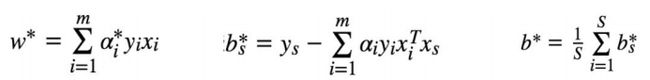
4.1.2、思路推导流程
4.1.2.1、函数最优化问题（无约束条件）
给定一个函数f(x)=x²+2x+3，找到一个x使得f(x)最小，对x的取值范围不做限制
4.1.2.2、函数最优化问题（有约束条件）
给定一个函数f(x)=x²+2x+3，找到一个x使得f(x)最小，但有约束条件x>=0
4.1.2.3、原始最优化问题
对应带约束带条件的最优化问题，其泛化表示形式为如下，s.t表示约束条件，即k个不等式约束条件和l个等式约束条件（SVM没有hj函数部分）
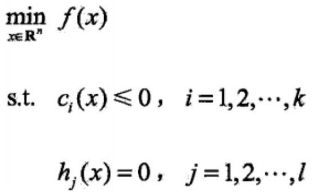
4.1.2.4、拉格朗日函数
使用拉格朗日函数的目的，是将有约束的最优化问题转换我无约束条件最优化问题，下面的式子与原始最优化问题式子等价；
定义一个原始最优化问题的拉格朗日函数，ci表示第i个不等式约束函数，βi表示第j个等式约束函数，αi和βi即为拉格朗日乘子。
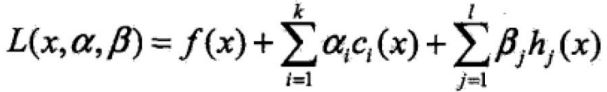
拉格朗日函数特性：令
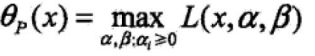
如果x满足上述s.t约束条件，则
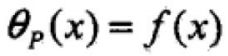
如果x不满足s.t约束条件，则
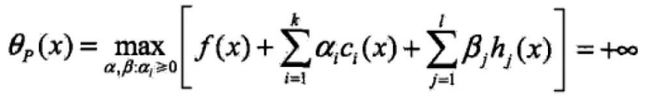
即
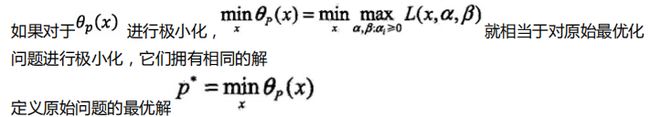
所以，对原始约束条件求最小，可以转换为先对拉格朗日函数函数求最大再求最小，即二次优化问题。也就是说，我们目标是求解x，但是会先在求最大值时解出α和β值，然后再将二者带入公式求最小值时解出x。
4.1.2.5、对偶问题
定义
此时求解θD极大值，则称为拉格朗日极大极小问题，也叫原始问题的对偶问题
其最优解形式为
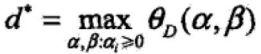
所以，当f(x)的ci函数为凸函数，hj函数为仿射函数（高维空间中的一条线），那么极小极大问题可以转换为极大极小问题（minmax=maxmin）
4.1.2.6、KKT条件求解
4.1.2.7、求解SVM最优化问题
4.1.2.7.1、整体流程
说明：之前的x表示w0-wn，而这里w表示w1-wn，b表示w0截距项，因为SVM不涉及β，所以函数式子中没有β
4.1.2.7.2、先求极小值（KKT条件）
4.1.2.7.3、再求极大值（将极小结果反代回公式）
4.1.2.7.4、整理对偶函数
4.1.2.7.5、求得最终超平面
4.2、软间隔SVM
4.2.1、硬间隔SVM面临的问题
硬间隔SVM要求完美的分割正负例样本，如果数据集线性不可分，包含噪声样本点，则意味着无法找到一个合格的超平面，也就是无法得出w和b的最优解
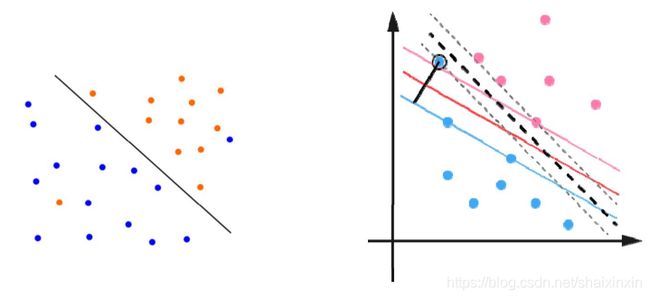
4.2.2、如何解决上述问题
引入松弛变量，将约束条件变为，ξ代表异常点嵌入间隔面的深度，我们要在能选出符合约束条件的最好的 w 和 b 的同时，让嵌入间隔面的总深度越少越好
4.2.3、目标函数优化
4.2.4、软间隔支持向量分析
4.2.5、软间隔最大化算法
1）设定惩罚系数C，构造优化问题
4.2.6、判别函数的另一种表达形式
4.3、非线性SVM与核函数
4.3.1、如何处理线性不可分问题
4.3.1.1、升维
4.3.1.2、核函数
4.3.2、svm算法求解流程
1）选择某个核函数及对应超参数
2）选择惩罚系数C
3）构造最优化问题
