机器学习(课堂笔记)Day03:kNN算法、分类准确度、超参数、网格搜索、数据归一化
目录
0x00 KNN (k近邻算法)
0x01 实现knn算法:
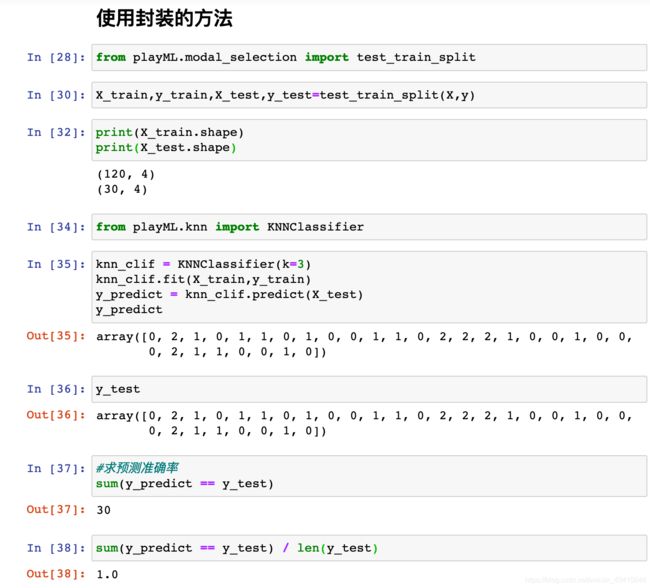
0x02 KNN 算法的封装
0x03 使用scikit-learn中kNN
0x04 重新整理我们之前封装的kNN分类器
0x05 判断机器学习算法的性能
#test_train_split 思路
## 封装成包
##使用 sklearn 中的 train_test_split
0x06 分类准确度
#scikit-learn中的accuracy_score
0x07 超参数
#关于距离:
0x08 网格搜索与k近邻算法中更多超参数
0x09 数据归一化
0x0A scikit-learn中的Scaler
0x0B 总结
0x00 KNN (k近邻算法)
思想:
两个样本如果足够相似(该相似性用特征空间中的样本之间的距离来描述)的话,他们就有可能属于同一个类别。
因为只看一个样本不够靠谱,所以我们 看和 新样本最近的 k个样本,k个样本中 那种样本最多,我们就认为新样本属于那种类别
例如:
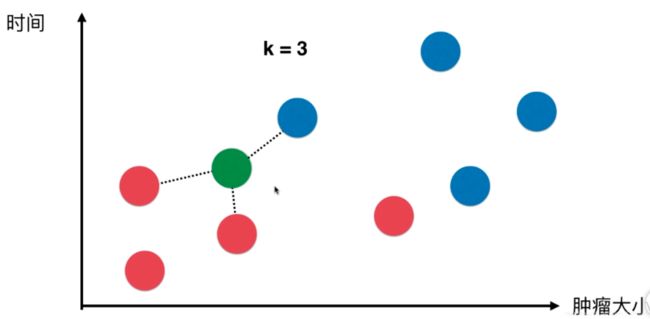
假设k=3 ,即我们只看和新样本距离最近的3个样本,他们都是蓝色,那么我们推测新样本也很有可能是蓝色
比如又来了一个新样本,距离它最近的三个样本,红色:蓝色 = 2:1,红色胜出,所以我们推测新样本很有可能是红色
0x01 实现knn算法:
补充知识:欧拉距离的高维推广
0x02 KNN 算法的封装
import numpy as np
from math import sqrt
from collections import Counter
# KNN分类算法
# X_train 训练矩阵
# y_train 训练标签
# x 新样本
def KNN_classify(k,X_train,y_train,x):
if(k<1 or k>=X_train.shape[0]):
print("k must be valid")
if(X_train.shape[0] != y_train.shape[0]):
print("the size of X_train must equal to the size of y_train")
if(X_train.shape[1] != x.shape[0]):
print("the feature number of x must be equal to X_train")
distances = [sqrt(np.sum((x_train - x)**2)) for x_train in X_train]
nearest = np.argsort(distances)
topK_y = [y_train[i] for i in nearest[:k]]
votes = Counter(topK_y)
return votes.most_common(1)[0][0]0x03 使用scikit-learn中kNN
机器学习算法 训练 模型的过程称为:fit 拟合
模型输出结果 的过程称为:predict 预测
knn算法并没有得到任何模型,可以说knn算法是一个不需要训练过程的算法
为了和其他算法统一,可以认为训练数据集就是模型本身
0x04 重新整理我们之前封装的kNN分类器
import numpy as np
from math import sqrt
from collections import Counter
class KNNClassifier:
def __init__(self, k):
assert k >= 1, 'k must be valid'
self.k = k
self._X_train = None # 私有变量
self._y_train = None
def fit(self, X_train, y_train):
assert X_train.shape[0] == y_train.shape[0],\
"the size of X_train must equal to the size of y_train"
assert self.k <= X_train.shape[0],\
"the size of X_train must be at least k"
self._X_train = X_train
self._y_train = y_train
return self
# 对一组新样本进行预测
def predict(self, X_predict):
assert self._X_train is not None and self._y_train is not None,\
"must fit before predict!"
assert self._X_train.shape[1] == X_predict.shape[1],\
"the feature number of x must be equal to X_train"
y_predict = [self._predict(x) for x in X_predict]
return np.array(y_predict)
# 对一个新样本进行预测
def _predict(self, x):
distances = [sqrt(np.sum((x_train - x)**2))
for x_train in self._X_train]
nearest = np.argsort(distances)
topK_y = [self._y_train[i] for i in nearest[:self.k]]
votes = Counter(topK_y)
return votes.most_common(1)[0][0]
def __repr__(self):
return "KNN(k=%d)" %self.k0x05 判断机器学习算法的性能
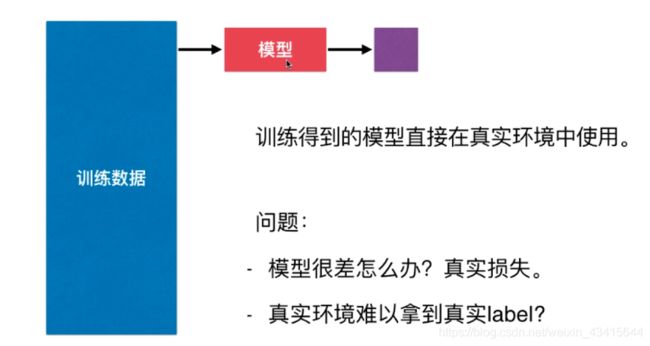
直接用所有的原始数据作为 训练数据 来训练模型的做法是不恰当的
建议将原始数据分为两部分:训练数据 和 测试数据 (train test split)
用训练数据训练出模型之后,将测试数据放入模型中去预测
因为测试数据本身具有label值,所以我们很容易测试出 模型的性能
#test_train_split 思路
## 封装成包
包结构:
modal_selection.py
import numpy as np
import matplotlib.pyplot as plt
def test_train_split(X,y,test_ratio=0.2,seed=None):
if seed:
np.random.seed(seed)
shuffle_indexes = np.random.permutation(len(X))
test_size = int(len(X) * test_ratio)#测试数据集的大小
test_indexes = shuffle_indexes[:test_size] #测试数据集对应索引
train_indexes = shuffle_indexes[test_size:] #训练数据集对应的索引
X_train = X[train_indexes]
y_train = y[train_indexes]
X_test = X[test_indexes]
y_test = y[test_indexes]
return X_train,y_train,X_test,y_test##使用 sklearn 中的 train_test_split
0x06 分类准确度
封装成包
metrics.py
import numpy as np
#计算y_true和y_predict的重合度
def accuracy_score(y_true,y_predict):
return sum(y_true == y_predict)/len(y_true)其实knn中可以封装一个准确度接口
import numpy as np
from math import sqrt
from collections import Counter
from .metrics import accuracy_score
class KNNClassifier:
def __init__(self, k):
assert k >= 1, 'k must be valid'
self.k = k
self._X_train = None # 私有变量
self._y_train = None
def fit(self, X_train, y_train):
assert X_train.shape[0] == y_train.shape[0],\
"the size of X_train must equal to the size of y_train"
assert self.k <= X_train.shape[0],\
"the size of X_train must be at least k"
self._X_train = X_train
self._y_train = y_train
return self
# 对一组新样本进行预测
def predict(self, X_predict):
assert self._X_train is not None and self._y_train is not None,\
"must fit before predict!"
assert self._X_train.shape[1] == X_predict.shape[1],\
"the feature number of x must be equal to X_train"
y_predict = [self._predict(x) for x in X_predict]
return np.array(y_predict)
# 对一个新样本进行预测
def _predict(self, x):
distances = [sqrt(np.sum((x_train - x)**2))
for x_train in self._X_train]
nearest = np.argsort(distances)
topK_y = [self._y_train[i] for i in nearest[:self.k]]
votes = Counter(topK_y)
return votes.most_common(1)[0][0]
def score(self,X_test,y_test):
y_predict = self.predict(X_test)
return accuracy_score(y_test,y_predict)
def __repr__(self):
return "KNN(k=%d)" %self.k
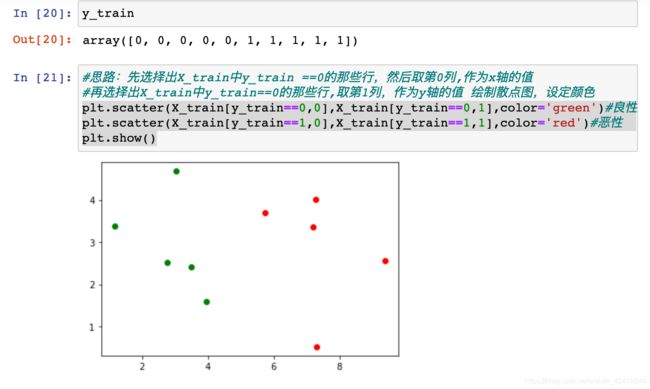
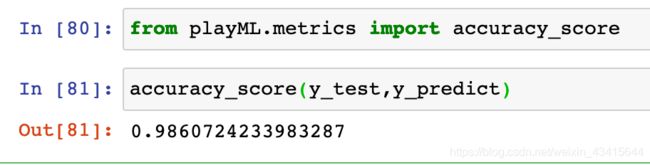
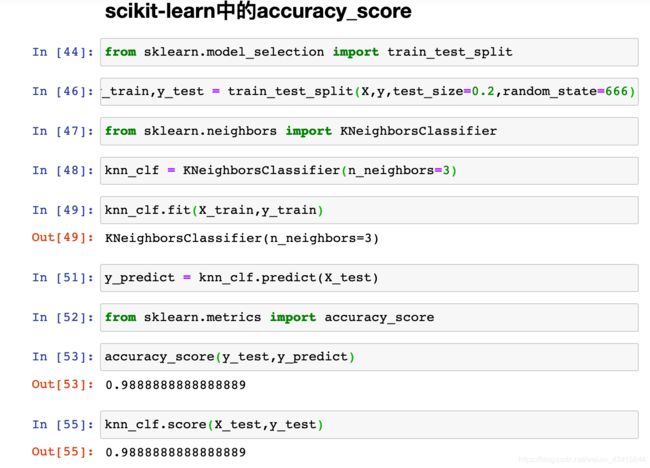
#scikit-learn中的accuracy_score
0x07 超参数
超参数:在算法运行前需要决定的参数
模型参数:算法过程中学习的参数
kNN算法没有模型参数,其中的k是典型的超参数
如何寻找好的超参数?
领域知识:不同领域中,超参数是不同的,通过领域知识寻找超参数
经验数值:通常封装好的经验数值都是一个比较好的超参数
实验搜索:测试几组不同的超参数,最终选效果最好的超参数
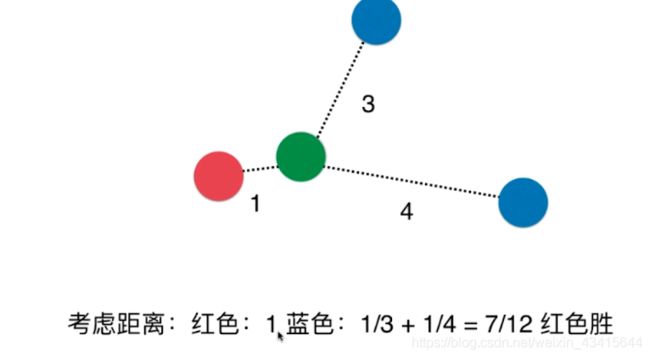
我们之前的k近邻算法只是考虑了距离新样本最近的点的label,而没有考虑到新样本周围k个点
距新样本的距离:
如果考虑到距离的权重,还会是蓝色获胜吗?
通常情况下,我们用距离的倒数作为距离的权重
普通的kNN算法还有一个问题:如果k=3 恰巧新样本周围有3类,那么就有可能出现平票的情况
uniform 不考虑距离权重,distance 考虑距离权重
#关于距离:
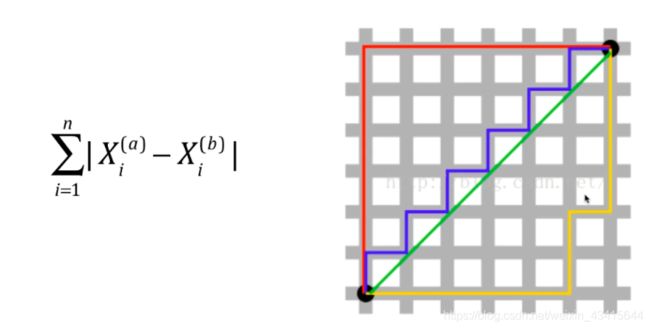
欧拉距离:
曼哈顿距离:
上图中绿色的线为 欧拉距离,红、蓝、黄都是曼哈顿距离
欧拉距离和 曼哈顿距离在数学形式 上是具有一致性的
我们将该一致性进行推广:
这就是明科夫斯基距离 Minkowski Distance
p = 1 时,明科夫斯基距离就相当于是曼哈顿距离
p = 2 时,明科夫斯基距离就相当于是欧拉距离
我们又获得了一个超参数:p
这种搜索策略就称为”网格搜索“:例如 k * p 就形成了一个二维的网格
0x08 网格搜索与k近邻算法中更多超参数
更多的距离定义:
0x09 数据归一化
数据归一化:将所有的数据都映射到同一尺度
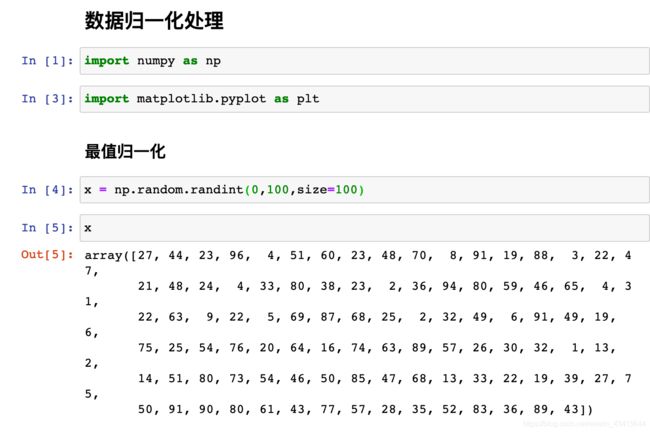
最值归一化(normalization):把所有的数据都映射到0-1之间
即求x-xmin 占 xmax-xmin 的比
适用于分布有明显边界的情况;受outlier影响较大
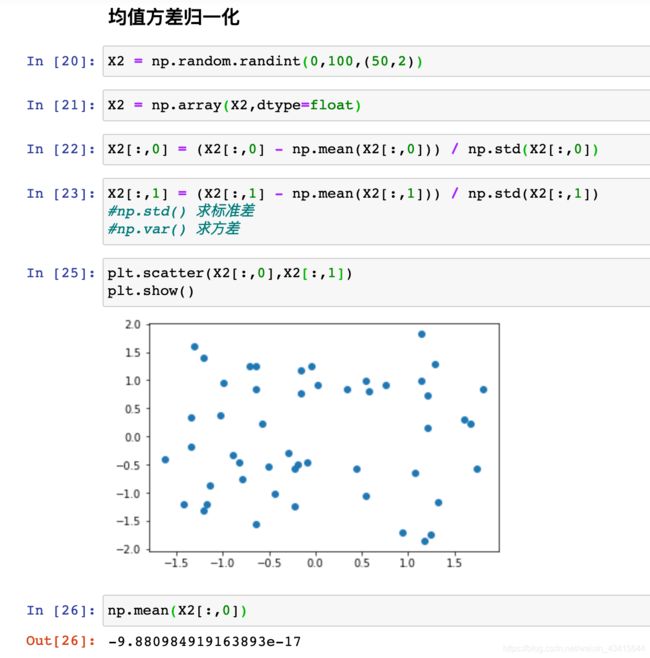
均值方差归一化 (standardization):将所有数据都归一到均值为0方差为1的分布中
适合于数据分布没有明显的边界;有可能存在极端数据值
(特征值 - 均值)/ 标准差 即该特征值和均值之间的差距 占 标准差的比
均值方差归一化的本质:将所有数的均值放在0的位置,将波动幅度(标准差)放在了1的位置
即便我们的数据中有 outlier 异常值(极端值) 也不会形成一个有偏的数据
0x0A scikit-learn中的Scaler
对测试数据集 如何归一化呢?
错误的做法:对测试数据集求mean_test 和 std_test
正确的做法: 继续使用mean_train 和std_train 对测试数据集进行 均值方差归一化
![]()
Why?
1.因为测试数据模拟的是真实环境,而真实环境 很有可能无法得到所有的测试数据的均值和方差
比如:鸢尾花分类中,真实环境中只来了一个新样本,我们如何求一个新样本的均值和方差呢?
2.对数据归一化也是算法的一部分
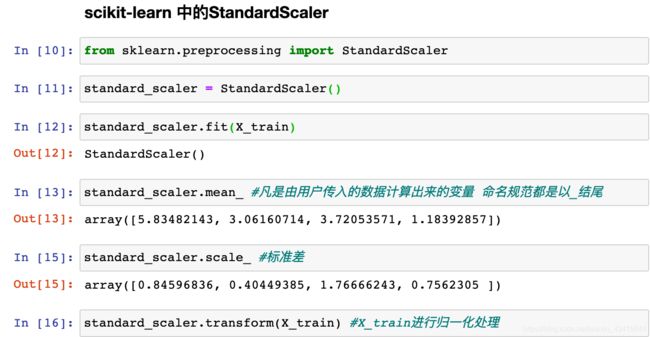
所以:我们需要保存训练数据集得到的均值和方差,scikit-learn中使用Scaler
fit :求训练数据集 相关的统计指标(均值,方差...)
封装成函数:
preprocessing.py
import numpy as np
class StandardScaler:
def __init__(self):
self.mean_ = None
self.scale_ = None
# 根据训练数据集X获得数据的均值和方差
def fit(self, X):
assert X.ndim == 2, "X的维度必须是2"
self.mean_ = np.array([np.mean(X[:, i]) for i in range(X.shape[1])])
self.scale_ = np.array([np.std(X[:, i]) for i in range(X.shape(1))])
return self
# 将X 进行数据归一化处理
def transform(self, X):
assert X.ndim == 2, "X的维度必须是2"
assert self.mean_ is not None and self.scale_ is not None,\
"在transform之前请先fit"
assert X.shape[1] == len(self.mean_),\
"列的数量必须和均值列数相匹配"
resX = np.empty(shape = X.shape,dtype=float)
for col in range(X.shape[1]):
resX[:,col] = (X[:,col] - self.mean_[col])/self.scale_[col]
return resX0x0B 总结
kNN 算法主要用来解决分类问题
并且天然可以解决多分类问题
虽然kNN算法的思想非常简单,但是它的分类效果却非常强大
kNN 算法 同样可以解决回归问题:即我们要预测的不是一个分类,而是一个数值
比如我们要预测房价、股票、学生的分数等
思想:新样本的值 是距离它最近的k个样本的平均值
同样我们可以考虑到距离权重,使用加权平均的方法进行预测
具体可以使用 该类:KNeighborsRegressor
参考文档:
kNN 算法的最大的缺点:效率低下
如果训练集有m个样本,n个特征,则预测每个新的数据,都需要计算
新样本和m个数据之间的距离,计算一个距离就需要O(n)的时间复杂度,计算
m个样本就需要O(m*n)
优化方式:使用树结构,KD-Tree Ball-Tree
缺点2:高度数据相关
即便是训练数据有2个outlier (异常点),都会对我们的预测结果准确度造成很大的影响
缺点3: 预测结果不具有可解释性
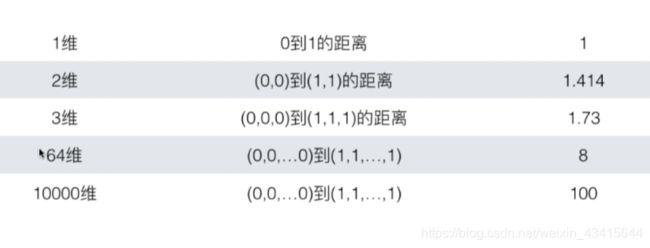
缺点4:维数灾难,随着维度的增加,”看似相近“的两个点之间的距离越来越大
维数灾难的解决方法:降维
机器学习流程回顾: