机器学习——LDA(线性判别分析)与人脸识别
目录
系列文章目录
一、LDA的概念与原理
1.LDA简介
2.LDA算法模型
3.LDA的优化问题
二、LDA运用于人脸识别
1.预处理
1.1 数据导入与处理
1.2 算各类均值、类间散度Sb、类内散度Sw
2.LDA核心(构造目标函数并对其进行特征分解)
3.人脸识别
4.LDA与PCA图像降维与可视化对比
5.LDA与PCA的异同总结
6.其他
6.1 内部函数定义
6.2 数据集及资源
6.3 参考资料
总结
系列文章目录
本系列博客重点在机器学习的概念原理与代码实践,不包含繁琐的数学推导(有问题欢迎在评论区讨论指出,或直接私信联系我)。
第一章 机器学习——PCA(主成分分析)与人脸识别_@李忆如的博客-CSDN博客
第二章 LDA与人脸识别
梗概
本篇博客主要介绍LDA(线性判别分析)算法并将LDA及其各种等价模型用于人脸的识别、图像降维可视化,并将LDA与PCA进行比较(内附数据集与matlab代码)
一、LDA的概念与原理
1.LDA简介
LDA(线性判别分析)为主流的一种线性降维算法。以”最小化类内方差,最大化类间方差“为目标导向,通过降维(投影),达到降维的目的更好地将样本分类。
2.LDA算法模型
经典的LDA解决问题可划分为以下步骤
1.将数据集分类,计算每个类的均值(LDA利用了样本的类别(数据)标签,为有监督学习)。
2.计算类间散度矩阵Sb与类内散度矩阵Sw。
3.构造目标函数(多种不同的目标函数)并对其进行特征分解。
4.取出一定数量的特征向量得到投影矩阵。
5.将测试数据投影到子空间中,使用KNN进行分类(实际问题中)。
3.LDA的优化问题
1.有限投影轴问题(≤类别数 - 1)
2.小样本问题
3.处理高维数据时,计算代价很大
优化:先用PCA进行预处理再使用LDA,或在目标函数中加入正则化扰动
4.不能较好地刻画非线性问题
优化:使用核属性的LDA升维处理数据
二、LDA运用于人脸识别
1.预处理
1.1 数据导入与处理
利用imread批量导入人脸数据库,或直接load相应mat文件,并在导入时不断将人脸拉成一个个列向量组成reshaped_faces,并取出30%作为测试数据,剩下70%作为训练数据,重复此步骤,将导入数据抽象成框架,可以匹配不同数据集的导入(本实验框架适配ORL、AR、FERET数据集)。
clear;
% 1.人脸数据集的导入与数据处理框架
reshaped_faces=[];
% 声明数据库名
database_name = "ORL";
% ORL5646
if (database_name == "ORL")
for i=1:40
for j=1:10
if(i<10)
a=imread(strcat('C:\Users\hp\Desktop\face\ORL56_46\orl',num2str(i),'_',num2str(j),'.bmp'));
else
a=imread(strcat('C:\Users\hp\Desktop\face\ORL56_46\orl',num2str(i),'_',num2str(j),'.bmp'));
end
b = reshape(a,2576,1);
b=double(b);
reshaped_faces=[reshaped_faces, b];
end
end
row = 56;
column = 46;
people_num = 40;
pic_num_of_each = 10;
train_pic_num_of_each = 7; % 每张人脸训练数量
test_pic_num_of_each = 3; % 每张人脸测试数量
end
%AR5040
if (database_name == "AR")
for i=1:40
for j=1:10
if(i<10)
a=imread(strcat('C:\AR_Gray_50by40\AR00',num2str(i),'-',num2str(j),'.tif'));
else
a=imread(strcat('C:\AR_Gray_50by40\AR0',num2str(i),'-',num2str(j),'.tif'));
end
b = reshape(a,2000,1);
b=double(b);
reshaped_faces=[reshaped_faces, b];
end
end
row = 50;
column = 40;
people_num = 40;
pic_num_of_each = 10;
train_pic_num_of_each = 7;
test_pic_num_of_each = 3;
end
%FERET_80
if (database_name == "FERET")
for i=1:80
for j=1:7
a=imread(strcat('C:\Users\hp\Desktop\face\FERET_80\ff',num2str(i),'_',num2str(j),'.tif'));
b = reshape(a,6400,1);
b=double(b);
reshaped_faces=[reshaped_faces, b];
end
end
row = 80;
column = 80;
people_num = 80;
pic_num_of_each = 7;
train_pic_num_of_each = 5;
test_pic_num_of_each = 2;
end
% 取出前30%作为测试数据,剩下70%作为训练数据
test_data_index = [];
train_data_index = [];
for i=0:people_num-1
test_data_index = [test_data_index pic_num_of_each*i+1:pic_num_of_each*i+test_pic_num_of_each];
train_data_index = [train_data_index pic_num_of_each*i+test_pic_num_of_each+1:pic_num_of_each*(i+1)];
end
train_data = reshaped_faces(:,train_data_index);
test_data = reshaped_faces(:, test_data_index);
dimension = row * column; %一张人脸的维度1.2 算各类均值、类间散度Sb、类内散度Sw
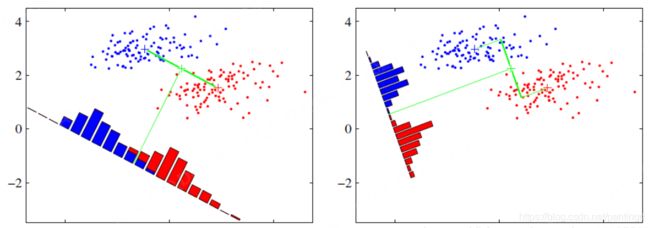
样本的类间散度矩阵Sb和类内散度矩阵Sw分别定义为:
图1 Sb与Sw的定义
将人脸数据集按人数n分为n类,算各类均值,并按Sb与Sw的定义与数学推导求出相应矩阵。
% 算每个类的平均
k = 1;
class_mean = zeros(dimension, people_num);
for i=1:people_num
% 求一列(即一个人)的均值
temp = class_mean(:,i);
% 遍历每个人的train_pic_num_of_each张用于训练的脸,相加算平均
for j=1:train_pic_num_of_each
temp = temp + train_data(:,k);
k = k + 1;
end
class_mean(:,i) = temp / train_pic_num_of_each;
end
% 算类类间散度矩阵Sb
Sb = zeros(dimension, dimension);
all_mean = mean(train_data, 2); % 全部的平均
for i=1:people_num
% 以每个人的平均脸进行计算,这里减去所有平均,中心化
centered_data = class_mean(:,i) - all_mean;
Sb = Sb + centered_data * centered_data';
end
Sb = Sb / people_num;
% 算类内散度矩阵Sw
Sw = zeros(dimension, dimension);
k = 1; % p表示每一张图片
for i=1:people_num % 遍历每一个人
for j=1:train_pic_num_of_each % 遍历一个人的所有脸计算后相加
centered_data = train_data(:,k) - class_mean(:,i);
Sw = Sw + centered_data * centered_data';
k = k + 1;
end
end
Sw = Sw / (people_num * train_pic_num_of_each);2.LDA核心(构造目标函数并对其进行特征分解)
Tips:本实验使用pinv(矩阵伪逆)代替inv(矩阵的逆),消除部分奇异值对实验带来的影响
每个目标函数对应不同LDA的等价模型(除法的、减法的及其调换位置的等)以及PCA模型(目标函数以及具体原理可以查看对应博客),确定目标函数后对其进行特征分解。
% 目标函数一:经典LDA(伪逆矩阵代替逆矩阵防止奇异值)
target = pinv(Sw) * Sb;
% 目标函数二:不可逆时需要正则项扰动
% Sw = Sw + eye(dimension)*10^-6;
% target = Sw^-1 * Sb;
% 目标函数三:相减形式
% target = Sb - Sw;
% 目标函数四:相除
% target = Sb/Sw;
% 目标函数五:调换位置
% target = Sb * pinv(Sw);
%PCA
% centered_face = (train_data - all_mean);
% cov_matrix = centered_face * centered_face';
% target = cov_matrix;
% 求特征值、特征向量
[eigen_vectors, dianogol_matrix] = eig(target);
eigen_values = diag(dianogol_matrix);
% 对特征值、特征向量进行排序
[sorted_eigen_values, index] = sort(eigen_values, 'descend');
eigen_vectors = eigen_vectors(:, index);3.人脸识别
降维过程LDA与PCA基本一致,在按特征值排好序的特征向量中取出前n大的特征向量来构建投影矩阵,实现降维(降维到n维),并用KNN进行分类预测,实现人脸识别,并比较PCA与LDA的各种等价模型与正则模型在不同数据集下的人脸识别精度。
Tips:单次运行为选定目标函数对应的人脸识别率。
% 人脸识别
index = 1;
X = [];
Y = [];
% i为降维维度
for i=1:5:161
% 投影矩阵
project_matrix = eigen_vectors(:,1:i);
projected_train_data = project_matrix' * (train_data - all_mean);
projected_test_data = project_matrix' * (test_data - all_mean);
% KNN的k值
K=1;
% 用于保存最小的k个值的矩阵
% 用于保存最小k个值对应的人标签的矩阵
minimun_k_values = zeros(K,1);
label_of_minimun_k_values = zeros(K,1);
% 测试脸的数量
test_face_number = size(projected_test_data, 2);
% 识别正确数量
correct_predict_number = 0;
% 遍历每一个待测试人脸
for each_test_face_index = 1:test_face_number
each_test_face = projected_test_data(:,each_test_face_index);
% 先把k个值填满,避免在迭代中反复判断
for each_train_face_index = 1:K
minimun_k_values(each_train_face_index,1) = norm(each_test_face - projected_train_data(:,each_train_face_index));
label_of_minimun_k_values(each_train_face_index,1) = floor((train_data_index(1,each_train_face_index) - 1) / pic_num_of_each) + 1;
end
% 找出k个值中最大值及其下标
[max_value, index_of_max_value] = max(minimun_k_values);
% 计算与剩余每一个已知人脸的距离
for each_train_face_index = K+1:size(projected_train_data,2)
% 计算距离
distance = norm(each_test_face - projected_train_data(:,each_train_face_index));
% 遇到更小的距离就更新距离和标签
if (distance < max_value)
minimun_k_values(index_of_max_value,1) = distance;
label_of_minimun_k_values(index_of_max_value,1) = floor((train_data_index(1,each_train_face_index) - 1) / pic_num_of_each) + 1;
[max_value, index_of_max_value] = max(minimun_k_values);
end
end
% 最终得到距离最小的k个值以及对应的标签
% 取出出现次数最多的值,为预测的人脸标签
predict_label = mode(label_of_minimun_k_values);
real_label = floor((test_data_index(1,each_test_face_index) - 1) / pic_num_of_each)+1;
if (predict_label == real_label)
correct_predict_number = correct_predict_number + 1;
end
end
correct_rate = correct_predict_number/test_face_number;
X = [X i];
Y = [Y correct_rate];
fprintf("k=%d,i=%d,总测试样本:%d,正确数:%d,正确率:%1f\n", K, i,test_face_number,correct_predict_number,correct_rate);
if (i == 161)
waitfor(plot(X,Y));
end
end图2 pinv改进的经典LDA在ORL下的人脸识别率与维数的关系
图3 LDA的各模型与PCA在FERET人脸识别率对比
分析:在FERET较大的数据集时,调换LDA、除法LDA、PCA的识别率波动较大,较其他三个模型识别率较低,而正则LDA与经典LDA在各数据集下表现相对稳定(其他图未展示),识别率均高于经典PCA,特别是在大数据集下,LDA相对PCA有明显优势。
4.LDA与PCA图像降维与可视化对比
分别使用PCA与LDA对人脸图像进行降维至2与3维,并取前三类的分布作图,将每类第一幅图作为代表图。
Tips:本实验以测试集的二三维可视化为例
% 二三维可视化
class_num_to_show = 3;
pic_num_in_a_class = pic_num_of_each;
pic_to_show = class_num_to_show * pic_num_in_a_class;
for i=[2 3]
% 取出相应数量特征向量
project_matrix = eigen_vectors(:,1:i);
% 投影
projected_test_data = project_matrix' * (reshaped_faces - all_mean);
projected_test_data = projected_test_data(:,1:pic_to_show);
color = [];
for j=1:pic_to_show
color = [color floor((j-1)/pic_num_in_a_class)*20];
end
% 显示
if (i == 2)
subplot(1, 7, [1, 2, 3, 4]);
scatter(projected_test_data(1, :), projected_test_data(2, :), [], color, 'filled');
for j=1:3
subplot(1, 7, j+4);
fig = show_face(test_data(:,floor((j - 1) * pic_num_in_a_class) + 1), row, column);
end
waitfor(fig);
else
subplot(1, 7, [1, 2, 3, 4]);
scatter3(projected_test_data(1, :), projected_test_data(2, :), projected_test_data(3, :), [], color, 'filled');
for j=1:3
subplot(1, 7, j+4);
fig = show_face(test_data(:,floor((j - 1) * pic_num_in_a_class) + 1), row, column);
end
waitfor(fig);
end
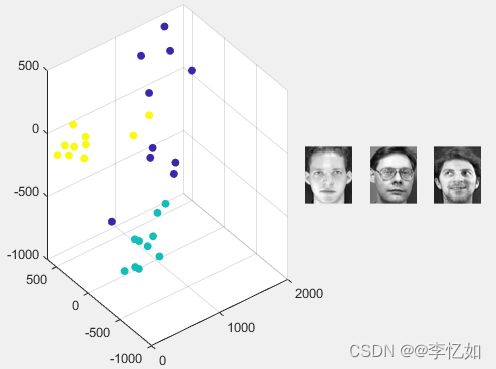
end图4 LDA在ORL数据集下二三维可视化
图5 LDA在ORL数据集下二三维可视化
分析:图4 图5(其他数据集与模型可自己更改目标函数或框架尝试)展示了LDA与PCA对图像的降维后分布,可以清晰地看出LDA降维同类图像较聚集,不同类图像较分散。而PCA则相对混杂,无明显规律。根据两算法的目的与原理,以此可以比较出PCA与LDA的不同(即eigenface与fisherface的不同)
5.LDA与PCA的异同总结
PCA LDA
分析:PCA与LDA都是常见的线性降维算法,但两算法的降维原理与目的不同,LDA的核心思想是“最小化类内方差,最大化类间方差”,从而更好地完成数据的分类与识别,而PCA的核心思想是“最小化协方差矩阵(最小化重构误差)”,从而实现数据的压缩与主成分重构,一般在小数据集下PCA与LDA效果相近甚至超过LDA,但在大数据集中,LDA明显优于PCA。另外,LDA使用了数据的标签(类别)信息,为有监督学习,而PCA则未使用,为无监督学习。
6.其他
6.1 内部函数定义
本实验中将人脸图像展示抽象为函数,函数定义如下:
% 输入向量,显示脸
function fig = show_face(vector, row, column)
fig = imshow(mat2gray(reshape(vector, [row, column])));
end6.2 数据集及资源
本实验以ORL5646数据集做展示,代码可适用多个数据集。
常用人脸数据集如下(不要白嫖哈哈哈)
链接:https://pan.baidu.com/s/12Le0mKEquGMgh5fhNagZGw
提取码:yrnb
LDA完整代码:李忆如/忆如的机器学习 - Gitee.com
6.3 参考资料
1.赖志辉的课
2.LDA算法原理及matlab实现_dulingtingzi的博客-CSDN博客_lda matlab
3.基于LDA的人脸识别方法--fisherface - 知乎 (zhihu.com)
4.周志华《机器学习》
总结
LDA作为经典的线性降维算法,通过”最小化内类方差,最大化类间方差“为目标导向对数据进行投影实现降维,更好地完成数据的分类。如今仍然在机器学习许多领域(数据分类、语言图像处理、推荐系统)有优异表现。且作为一种有监督学习方法(利用了数据的原有信息),LDA能得到较好的保留数据信息。但LDA仍存在上文提到的有限投影轴问题、小样本问题、处理高维数据大计算代价问题、不好刻画非线性问题等等,另外,LDA是假设每个类的数据都是高斯分布的情况下开发的,这个属性在现实世界的问题中往往不存在。如果没有这个属性,不同类的可分离性就不能很好地通过类间散射来描述,从而影响实验结果,后续博客会分析其他算法优化或解决上述问题。