【paper reading】MVSNet: Depth Inference for Unstructured Multi-view Stereo
【paper reading】MVSNet: Depth Inference for Unstructured Multi-view Stereo
- 1.简介
- 2.相关工作
- 3.MVSNet
-
- 3.1 Images to Deep Features
- 3.2 Deep Features to Feature Volumes
- 3.3 Feature Volumes to Cost Volume
- 3.4 Cost Volume to Probability Volume
- 3.5 Probability Volume to Depth Map
- 3.6 Depth Map Refinement
- 3.7 网络Loss
- 3.8 Depth Map Filter
- 4.方法性能
- 5.总结
这篇文章是在ECCV’ 18上发表的一篇论文,是香港科技大学权龙教授团队的工作,当时在会上被选作Oral,值得一读。
1.简介
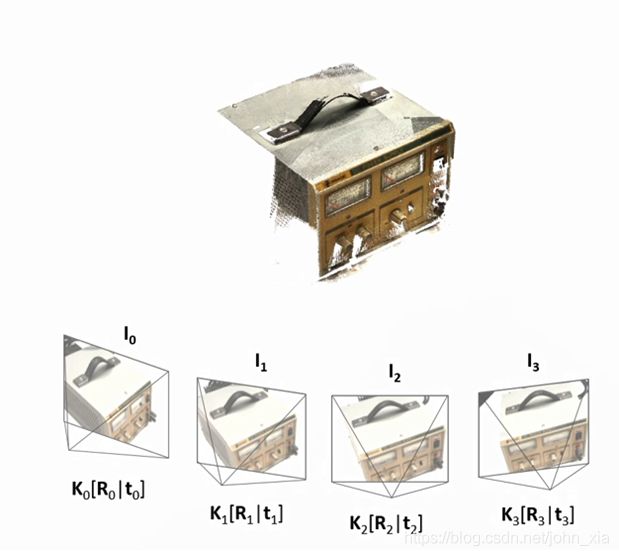
MVSNet,顾名思义,就是非结构化多视图的三维重建网络,它的输入这里要注意的是不仅仅是多个视角下拍摄的图像,还包含相机的信息,然后输出是每个视图下的深度信息,最终可以将这些深度信息融合得到最终的三维点云。
2.相关工作
传统的一些Multi-view方法使用的是人为设计的相似性度量和正则化,像NCC(归一化互相关)和SGM(半全局匹配)来计算密集的对应关系以及恢复三维点信息。
这些人为设计方法在理想的实验环境下效果很好,但是不能对抗弱纹理、高光、反射这些情况,最终导致的结果就是目前的state-of-the-art的方法经常在精度上十分精准,但是完整性上表现的不尽人意。例如下图中,左边为2010年的PMVS方法,右边为Ground-Truth,在仪器的顶部和前方面板上由于弱纹理,方法最终重建的结果缺失严重。
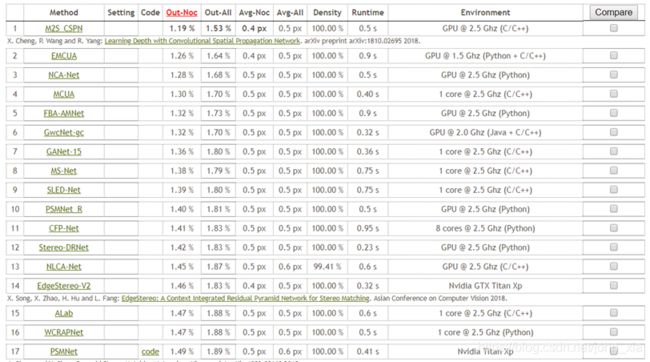
但是最近的一些基于学习的方法表现出了在这些非理想环境下的良好的鲁棒性,例如在立体匹配领域,由于图像对良好的组织性,也更加适合基于神经网络的方法的发展。像目前KITTI 数据集上,排在前位的大部分都是神经网络方法。
再回到Multi-View上,其实之前就已经有人在这方面用神经网络做过一些工作。例如论文里经常提到的ICCV’ 17上的SurfaceNet和NIPS’ 17上的Learned Stereo Machine (LSM),但是他们都是基于volumetric重建的,代价就是空间离散带来的误差以及内存消耗。因此LSM只能处理一些合成物体并且最终重建的分辨率较低。而SurfaceNet则使用启发式的分治策略,需要花很长时间才能进行大尺度的重建。也正是由于这些原因,MVSNet选择基于深度图重建。
三维重建中基于输出方式分类:
- 直接点云重建 缺点:难以做到充分的并行处理
- volumetric重建 缺点:空间离散带来的误差以及内存消耗较大
- 深度图重建
而对于Multi-View,它与双目立体匹配相比还有一些新的挑战,首先是相机的空间结构可以是任意的,没有双目立体匹配那么规则。另外一个就是Multi-View的输入图像数量可能是任意多的,因此要求算法能够处理任意数目的图像输入。而且场景多种多样,但是能够使用的Multi-View数据集相对来讲规模并没有其他领域那么大,Multi-View要求算法对场景类别要有强的泛化能力。
3.MVSNet
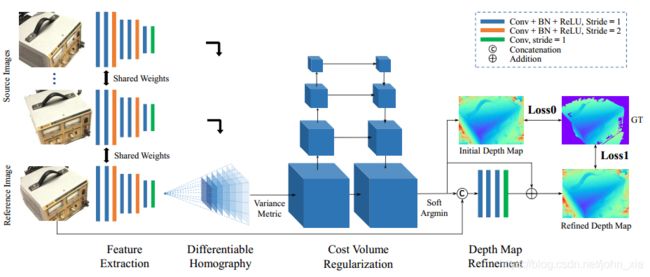
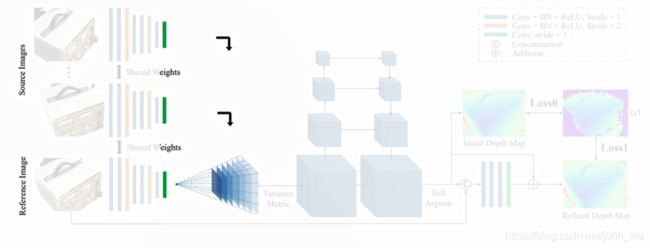
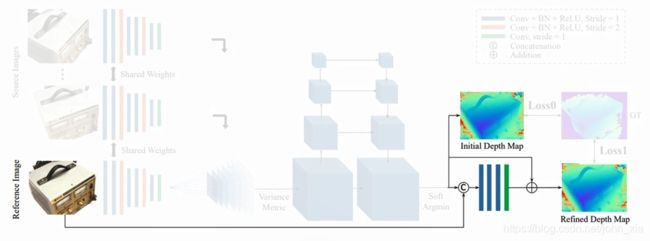
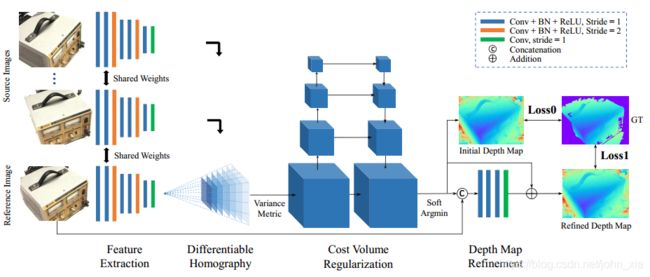
MVSNet是一个端到端的网络架构。它的输入是一副参考图像和几张其他的图像,最终预测出的是参考图像的深度图。每次选择不同的图像作为参考图像就能得到各个视角下的深度图。
3.1 Images to Deep Features
I m a g e s { I i } i = 1 N → 2 D C N N s D e e p F e a t u r e s { F i } i = 1 N \mathrm {Images}\ \{\mathbf {I}_i\}^{N}_{i=1}\xrightarrow{\color{blue} \mathrm {2D\ \ CNNs}}\mathrm {Deep\ Features}\ \{\mathbf {F}_i\}^{N}_{i=1} Images {Ii}i=1N2D CNNsDeep Features {Fi}i=1N
首先对于每一幅图像 I i \mathbf {I}_i Ii,全都要通过8层的CNN来提取图像的Feature Map F i \mathbf {F}_i Fi。这里第三层和第六层的卷积步长是2,因此最后得到的是N个32通道的Feature Map,并且长宽都是原始图像的1/4。虽然特征图缩小了,但是每个特征图像素包含了原始像素周围的信息,因此在最终的细化过程中不会丢失细节信息。
3.2 Deep Features to Feature Volumes
D e e p F e a t u r e s { F i } i = 1 N → C a m e r a s F e a t u r e V o l u m e s { V i } i = 1 N \mathrm {Deep\ Features}\ \{\mathbf {F}_i\}^{N}_{i=1}\xrightarrow{\color{blue} \mathrm {Cameras}}\mathrm {Feature\ Volumes}\ \{\mathbf {V}_i\}^{N}_{i=1} Deep Features {Fi}i=1NCamerasFeature Volumes {Vi}i=1N
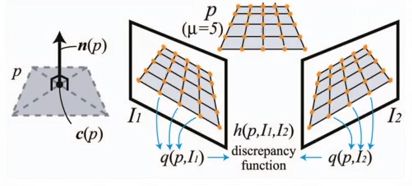
接下来是论文的一个主要的创新,这里它提出了一个基于单应变换的2D到3D的转换方法,并且将相机的几何关系结合到神经网络中。就是将其他图像的Feature通过可微的单应变换,warp到参考图像相机前的这些平行平面上,这一步的转换根据如下的单应矩阵进行计算。利用2D的feature生成3D的Feature Volume。就是他把其他图像上的feature warp到参考图像的相机视锥中的256个深度平面上,总有一个深度是对应的。第 i i i个feature warp到参考图像相机视锥的深度 d d d平面的单应矩阵 H i ( d ) \mathbf {H}_i(d) Hi(d)是通过下面的公式计算的:
H i ( d ) = K i ⋅ R i ⋅ ( I − ( t 1 − t i ) ⋅ n 1 T d ) ⋅ R 1 T ⋅ K 1 T \mathbf {H}_i(d)=\mathbf {K}_i\cdot\mathbf {R}_i\cdot(\mathbf {I}-{(\mathbf {t}_1-\mathbf {t}_i)\cdot\mathbf {n}^{T}_1\over d})\cdot\mathbf {R}^{T}_1\cdot\mathbf {K}^{T}_1 Hi(d)=Ki⋅Ri⋅(I−d(t1−ti)⋅n1T)⋅R1T⋅K1T
其中 K i \mathbf {K}_i Ki、 R i \mathbf {R}_i Ri、 K 1 \mathbf {K}_1 K1、 R 1 \mathbf {R}_1 R1、 t i \mathbf {t}_i ti、 t 1 \mathbf {t}_1 t1分别是其他图像与参考图像的相机内参矩阵与相机旋转矩阵和位移向量。 n 1 \mathbf {n}_1 n1是参考图像相机的principle axis。 d d d表示深度,取256个固定值。 I \mathbf I I是单位矩阵。
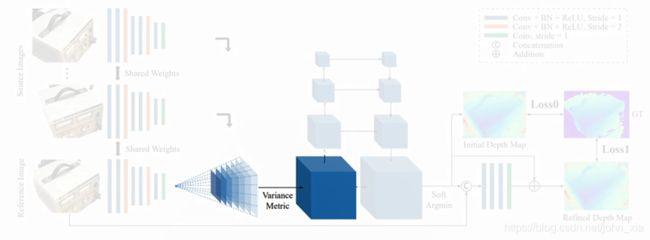
3.3 Feature Volumes to Cost Volume
F e a t u r e V o l u m e s { V i } i = 1 N → V a r i a n c e C o s t V o l u m e C \mathrm {Feature\ Volumes}\ \{\mathbf {V}_i\}^{N}_{i=1}\xrightarrow{\color{blue} \mathrm {Variance}}\mathrm {Cost\ Volume}\ \mathbf {C} Feature Volumes {Vi}i=1NVarianceCost Volume C
经过可微单应变换的步骤之后,得到的是N个feature volume,每个feature volume的大小是 W 4 ⋅ H 4 ⋅ D ⋅ F {W\over 4}\cdot{H\over 4}\cdot D\cdot F 4W⋅4H⋅D⋅F。 W 4 ⋅ H 4 {W\over 4}\cdot{H\over 4} 4W⋅4H就是之前由于两个步长为2的卷积层造成的缩放结果。D是深度采样数,论文里从425mm到935mm以2mm为间距采样256个深度,就是之前单应变换矩阵中d的取值数目。F是feature map的通道数,就是32。接下来要做的就是把这N个feature volume合并成一个cost volume。这里论文里提到,之前的一些方法大多采用取平均的做法。但是平均操作本身而言并没有产生更多的信息,因此作者在这里使用的是基于方差的操作,逐像素地求cost volume。
C = M ( V i , … , V N ) = ∑ i = 1 N ( V i − V i ‾ ) 2 N \mathbf C=\mathcal M(\mathbf {V}_i,…,\mathbf {V}_N)={\sum_{i=1}^N (\mathbf {V}_i-\overline{\mathbf {V}_i})^2\over N} C=M(Vi,…,VN)=N∑i=1N(Vi−Vi)2
这个操作可以输入任意数目的feature volume,因此整个网络能够处理任意数目的原始图像输入。
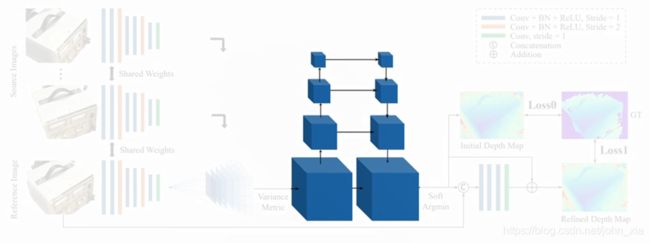
3.4 Cost Volume to Probability Volume
C o s t V o l u m e C → 3 D C N N s P r o b a b i l i t y V o l u m e P \mathrm {Cost\ Volume}\ \mathbf {C}\xrightarrow{\color{blue} \mathrm {3D CNNs}}\mathrm {Probability\ Volume}\ \mathbf {P} Cost Volume C3DCNNsProbability Volume P
之后得到的cost volume经过一个四级的U-Net结构来生成一个probability volume。这个probability volume其实就是在每个深度下,每个像素的可能性大小。
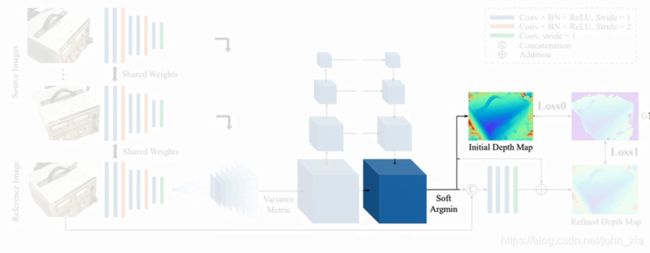
3.5 Probability Volume to Depth Map
P r o b a b i l i t y V o l u m e P → E x p e c t a t i o n D e p t h M a p D \mathrm {Probability\ Volume}\ \mathbf {P}\xrightarrow{\color{blue} \mathrm {Expectation}}\mathrm {Depth\ Map}\ \mathbf {D} Probability Volume PExpectationDepth Map D
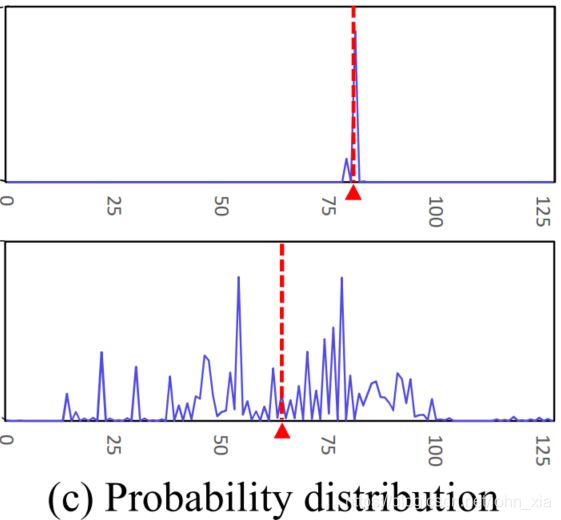
现在知道了在深度上的概率分布,就可以计算一个初始的深度图。这里最简单的策略就是winner takes all,选概率最大的深度作为点的深度,但是这也会带来问题,理想情况下概率分布只有一个很尖锐的波峰,这肯定是没问题的。但是在有多个波峰的情况下,这个策略就不是特别有效。另一个问题就是这个做法不是可微的,因此最终的做法是计算深度的数学期望作为初始深度图D的结果。
D = ∑ d = d m i n d m a x d × P ( d ) \mathbf D=\sum_{d=d_{min}}^{d_{max}} {d\times \mathbf P(d)} D=d=dmin∑dmaxd×P(d)
3.6 Depth Map Refinement
D → 2 D C N N s D r e f i n e \mathbf {D}\xrightarrow{\color{blue} \mathrm {2D \ CNNs}}\mathbf {D}_{\mathrm {refine}} D2D CNNsDrefine
由于得到的初始深度图在物体边缘还是不够精细,因此使用原始图像信息来进行细化。这里是将深度图与原始图像串连成一个四通道的输入,经过神经网络得到深度残差,然后加到之前的深度图上从而得到最终的深度图。
3.7 网络Loss
整个网络最终的loss很简单就是两个部分,初始深度图到Ground-Truth的L1距离和细化后深度图到Ground-Truth的L1距离。
L o s s = ∑ p ∈ p v a l i d ∥ d ( p ) − d i ^ ( p ) ∥ 1 + λ ⋅ ∥ d ( p ) − d r ^ ( p ) ∥ 1 Loss = \sum_{p\in\mathbf p_{valid}}\lVert d(p) -\hat{d_i}(p)\rVert_1+\lambda\cdot\lVert d(p) -\hat{d_r}(p)\rVert_1 Loss=p∈pvalid∑∥d(p)−di^(p)∥1+λ⋅∥d(p)−dr^(p)∥1
d ( p ) d(p) d(p)是GT的Depth Map, d i ^ ( p ) \hat{d_i}(p) di^(p)是Initial Depth Map的值, d r ^ ( p ) \hat{d_r}(p) dr^(p)是Refined Depth Map的值。由于GT中不是每个点都有值,所以只在GT有值的区域,即 p ∈ p v a l i d p\in\mathbf p_{valid} p∈pvalid中求Loss。
3.8 Depth Map Filter
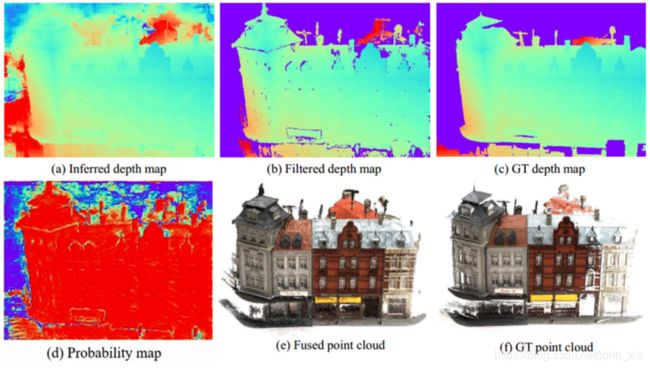
最后得到的深度图是左上角的这样,可以看到有很多地方都是错的。因此这里需要滤除这些错误的深度。这里要用到之前的概率分布的提供的信息。
像素深度的概率分布能显现出最终结果的质量。理想状态下在真实深度附近概率应该很高形成一个峰,像上面这样,因此对于之前采样的256个深度,取最接近期望的四个深度,他们概率的和应该大于0.8,才能确信这个是正确的,否则就将其视为outlier。另外对于每个视角下的点的深度,将它投影到其他视角下,需要和那个视角的深度图信息相符合,就称他为两视角一致。最终只保留那些三视角下一致的点。
最终经过过滤得到的是每个视图下的深度图,将这些深度图经过深度融合得到最终的三维点云。
4.方法性能
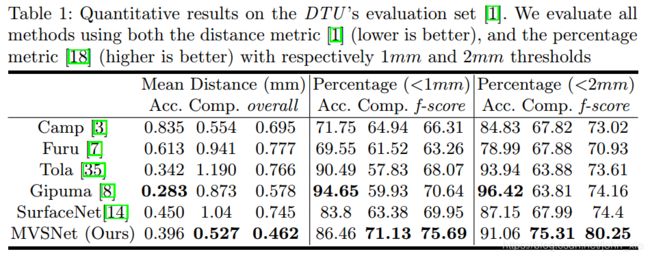
MVSNet是在DTU数据集上进行训练的。最终的评测结果表里面,前面这一项mean distance是最终深度值与GT的差异,越低越好,后面两项Percentage是越高越好。可以看到最终在准确性上虽然还是Gipuma更高一些,但是完整性上MVSNet有了很大的改善。f-score是把前面的精确度和完整度加起来看的结果,也有很大的进步。
在速度上也比其他方法更快,每个视角的深度图计算时间是4.7秒,比Gipuma快5倍,比COLMAP快100倍,比SurfaceNet快160倍。
可以看到在最终的重建点云结果中,完整性有了显著的改善。尤其是在弱纹理区域,完整性接近于GT。
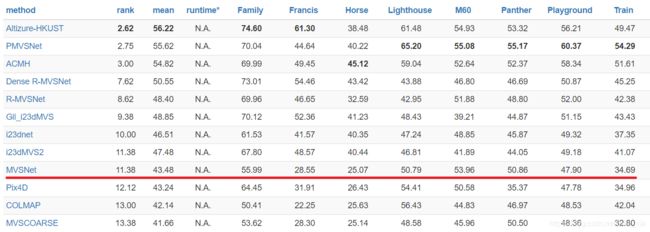
另外也在Tanks and Temples数据集上验证了自己的方法。由于数据集给出的GT的格式问题,MVSNet并没有在这个数据集上进行fine-tune,但是依旧能表现出良好的泛化能力。它在18年4月前当时是排第一的,截至19年3月4日排在第9位。
论文中还对网络进行了一些讨论。
作者尝试了使用不同数量的图像来进行重建。网络使用3个视角下的图像作为输入训练,但是测试的时候分别输入2,3,和5张图像,validation loss随着视角的增多明显下降。验证了MVSNet应对不同数目的输入图像的泛化能力。
右侧图中最上面的蓝线是在提取feature map的时候只是用一层神经网络,模拟传统的图像块特征的效果。紫色的是在N个feature volume合并成一个cost volume阶段,直接采用平均得到的结果。绿色是没有进行深度值细化步骤的结果,可以看到它其实误差比现在的MVSNet还要小,但是误差<1mm和误差<2mm的比较下总体得分其实还是更低的。
5.总结
总体而言,论文的创新主要是
- 使用了可微单应变换操作,将相机的几何信息encode到网络中,将2D的图像feature转换到3D的cost volume;
- 它的3D cost volume是建立在相机视锥的基础上的而不是普通的欧式空间;
- 通过基于方差的N个feature volume合并成一个cost volume的过程,能适应不同数目的多视角图像输入。