SVM支持向量机的python实现
写在前面
博主现在在学《统计学习方法》这本书,折腾支持向量机也有半个月多了,之前一直想要把支持向量机搞懂,所以就想集中一段时间来学支持向量机,但是因为懒惰,断断续续地磨了很久。这两天终于实现了支持向量机,这里想把代码分享给大家。
代码主要参考了两个网友的实现,这里给出参考的网页链接:1)参考代码1;2)参考代码2。
参考的两个代码都有比较模糊的地方。而我的代码也没好到哪里去,但是代码中每个地方对应于什么内容都有注释,相对会比较清晰些。我也给出了两个小的数据集用于训练,数据集的特征都是2维的,所以训练完后可以画出决策边界,就没用测试集了,因为直接看决策边界的效果也比较清楚。其中第1个训练集是来自于是「参考代码2」的,第2个训练集是吴恩达机器学习作业6中的。我会上传到资源,供大家下载测试。
对于支持向量机的内容,我这里不做详细的讲解,因为网上也有挺多不错的讲解了,我这里给出我自己的学习SVM用到的资料:
1)《统计学习方法》
2)零基础学SVM
3)支持向量机(SVM)原理剖析及实现
4)李航统计学习之SVM支持向量机+SMO算法数学推导
课本上有些地方没有说清楚,所以另外找些学习资料还是很有必要的,但是我还是有些地方不明白呀。刚开始学支持向量机的同学,强烈建议先看「零基础学SVM」,这里面讲清楚了对偶问题。然后软间隔和核函数那里,可以看最后两个资料,最后的那个视频资料我觉得很不错,跟着视频公式推下来,多看几遍就差不多了。个人觉得支持向量机还是有一定难度的,需要花点时间来学,反正我是真的花了挺多时间的。
代码思路说明
这个代码我是按照《统计学习方法》中SMO算法的描述来实现的,代码的整个框架其实就是两个 α \alpha α变量的选择。
1)关于第一个 α \alpha α的选择,书中说首先遍历所有满足条件 0 < α i < C 0<\alpha_i
2)关于第二个 α \alpha α的选择,书中说是希望选择的第二个 α \alpha α能使 α 2 \alpha_2 α2有足够大变化,即使 ∣ E 1 − E 2 ∣ \vert E_1-E_2 \vert ∣E1−E2∣最大。那么这里我就直接把 E 1 E_1 E1与所有样本的 E E E值作差,然后选出使 ∣ E 1 − E ∣ \vert E_1-E \vert ∣E1−E∣最大的样本作为第2个 α \alpha α变量。之后,就是对 α 1 \alpha_1 α1、 α 2 \alpha_2 α2、 E 1 E_1 E1和 E 2 E_2 E2等的更新了。直接看代码可能思路会更清晰些,如果有不太明白的,直接评论里问。
参数的话我没调,核函数的 σ \sigma σ设为0.1, C C C设为200。挺多代码都这么设,画出的决策边界结果也还可以。
训练结果图
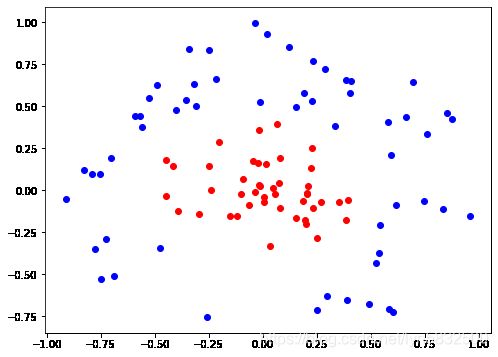
dataset_1
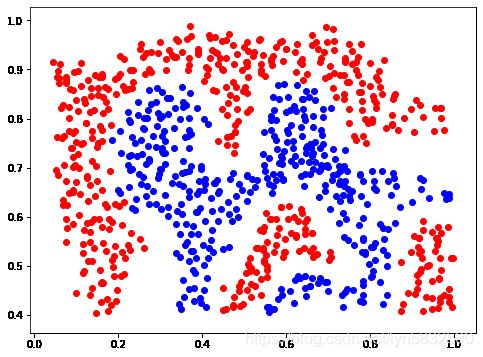
dataset_2
数据集下载
数据集是.mat文件,使用scipy模块来读取文件。
两个数据集都为2维,样本数分别为100和863。
数据集
代码
我写python代码习惯在句尾加’;’,请见谅~
本代码中包括打印原始数据集、支持向量和决策边界,直接调用对应的方法即可。
代码直接复制到jupyter notebook就能运行,最好把代码分开,不要全放在一个代码框中。需要修改的只有数据集的路径。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.io as scio
import random
def load_data(path):
"""
读取数据
param
path: 数据路径
"""
data = scio.loadmat(path);
X_train = data1['X'];
y_train = data1['y'];
y_train = y_train1.reshape(-1); # 标签转为向量
return X_train, y_train;
class SVM:
def __init__(self, train_data, train_label, sigma = 0.1, C = 100, epsilon = 0.0001, iter_time = 30):
"""
初始化函数
param
train_data: 训练集
train_label: 训练标签
sigma: 高斯核函数的参数
C: 软间隔的惩罚系数
epsilon: 精度
iter_time: 迭代次数
"""
self.train_data = train_data; # 训练特征集
self.train_label = train_label; # 训练标签
self.sigma = sigma; # 高斯核函数参数
self.C = C; # 惩罚项系数
self.epsilon = epsilon; # 精确值
self.iter_time = iter_time; # 迭代次数
self.G = np.zeros(train_data.shape[0]); # G值
self.E = -1 * train_label.copy(); # E值
self.alpha = np.zeros(train_data.shape[0]); # 拉格朗日参数
self.b = 0;
self.m = train_data.shape[0]; # 样本数
self.supportVecIndex = []; # 支持向量
def gaussian_kernel(self, i):
"""
高斯核函数,向量化计算K(j,i),即一次性计算出K(1,i), K(2,i),...,K(m,i),m是样本数
param
i: 需要计算的那个样本的编号
return
K: 是i与每个样本的核函数结果向量
"""
K = np.exp(-1 * np.sum((self.train_data - self.train_data[i])**2, axis = 1) / (2 * self.sigma**2));
return K;
def single_gaussian_kernel(self, i, j):
"""
计算单个高斯核函数,不使用向量化,单独计算K(i,j)
param
i: 第1个样本编号
j: 第2个样本编号
"""
K = np.exp(-1 * np.sum((self.train_data[i] - self.train_data[j])**2) / (2 * (self.sigma ** 2)));
return K;
def compute_G(self, i):
"""
计算第i个样本的G值
param
i: 计算的那个样本的编号
"""
K_i = self.gaussian_kernel(i); # 计算这个样本的高斯核函数结果
G = np.sum(self.alpha * self.train_label * K_i) + self.b;
return G;
def compute_E(self, i):
"""
计算第i个样本的E值
param
i: 样本的编号
"""
G_i = self.compute_G(i); # 计算这个样本的G值
E = G_i - self.train_label[i];
return E;
def gaussian_kernel_for_test(self, x):
"""
用于计算预测样本的高斯核函数,使用样本特征作为输入
param
x: 输入样本
return
K: 预测样本与每个样本的结果向量
"""
K = np.exp(-1 * np.sum((self.train_data - x)**2, axis = 1) / (2 * self.sigma**2));
return K;
def compute_G_for_test(self, x):
"""
计算预测样本的G值
param
x: 输入样本
"""
K_i = self.gaussian_kernel_for_test(x); # 计算这个样本的高斯核结果
G = np.sum(self.alpha * self.train_label * K_i) + self.b;
return G;
def judge_KKT(self, i):
"""
判断第i个样本是否满足KKT
return
True: 满足KKT条件
False: 不满足
"""
Ei = self.compute_E(i);
# 该语句用于判断是否满足3条KTT条件
if (((self.train_label[i] * Ei < -self.epsilon) and (self.alpha[i] < self.C)) or ((self.train_label[i] * Ei > self.epsilon) and (self.alpha[i] > 0))):
return False;
return True;
def select_second_alpha(self, i):
"""
选出第二个alpha
param
i: 选中的第1个alpha的编号
return
j: 第二个alpha的索引
"""
delta_Es = abs(self.E - self.E[i]); # 计算第i个样本的E与所有的其他样本的E差
delta_Es[i] = -1; # 把与自己的差值设为负的,防止选到自己
j = np.argmax(delta_Es);
return j
def update(self, i, j, E1, E2):
"""
选择好两个alpha后,更新alpha,如果alpha变化太小则直接退出
parame
i: 第一个alpha的编号
j: 第二个alpha的编号
E1: 第1个alpha样本的E值
E2: 第2个alpha样本的E值
return
True: 成功更新
False: 未进行更新,返回重新选择alpha
"""
# 计算未经剪辑的alpha2的解
x1, x2 = self.train_data[i], self.train_data[j]; # 选择的第1个和第2个alpha的样本
y1, y2 = self.train_label[i], self.train_label[j]; # 选择的第1个和第2个alpha的样本标签
alpha1, alpha2 = self.alpha[i], self.alpha[j]; # 选择的第1个和第2个alpha
self.single_gaussian_kernel(i, j)
K11, K12, K22 = self.single_gaussian_kernel(i, i), self.single_gaussian_kernel(i, j), self.single_gaussian_kernel(j, j);
eta = K11 + K22 - 2 * K12;
alpha2_new_unc = self.alpha[j] + (self.train_label[j] * (E1 - E2) ) / eta; # 未经剪辑的alpha2的解
# 剪辑解
if (y1 == y2):
L = max(0, alpha1 + alpha2 - self.C);
H = min(self.C, alpha1 + alpha2);
else:
L = max(0, alpha2 - alpha1);
H = min(self.C, self.C + alpha2 - alpha1);
if (alpha2_new_unc<=H and alpha2_new_unc>=L):
alpha2_new = alpha2_new_unc;
elif (alpha2_new_unc < L):
alpha2_new = L;
else:
alpha2_new = H;
if (abs(alpha2_new - alpha2) < 0.00001): # 如果更新太小,直接return,重新选择
return False
alpha1_new = alpha1 + y1 * y2 * (alpha2 - alpha2_new);
self.alpha[i] = alpha1_new; # 更新alpha1
self.alpha[j] = alpha2_new; # 更新alpha2
# 更新b
b1 = -1 * E1 - y1 * K11 * (alpha1_new - alpha1) - y2 * K12 * (alpha2_new - alpha2) + self.b;
b2 = -1 * E2 - y1 * K12 * (alpha1_new - alpha1) - y2 * K22 * (alpha2_new - alpha2) + self.b;
# 确定b
if (alpha1_new < self.C and alpha1_new > 0):
self.b = b1;
elif (alpha2_new < self.C and alpha2_new > 0):
self.b = b2;
else:
self.b = (b1 + b2) / 2;
self.E[i] = self.compute_E(i); # 更新E1
self.E[j] = self.compute_E(j); # 更新E2
return True;
def train(self):
"""
使用SMO算法进行训练
"""
iter_time = 0; # 当前的循环次数
entire_flag = True; # 是否进行整个数据集遍历的标记
parameterChanged = 1; # 记录参数改变的次数
while (iter_time < self.iter_time and parameterChanged > 0 or entire_flag):
parameterChanged = 0;
if (entire_flag):
entire_flag = False; # 下次对支持向量进行遍历
for i in range(self.m): # 遍历每个样本,选择第1个alpha
if (not self.judge_KKT(i)): # 如果这个样本不满足KKT条件,则作为第1个alpha,然后选择第2个alpha
self.E[i] = self.compute_E(i); # 第1个alpha样本的E值
j = self.select_second_alpha(i); # 选择第2个alpha
self.E[j] = self.compute_E(j); # 第2个E值
flag = self.update(i, j, self.E[i], self.E[j]);
if (flag == True):
parameterChanged += 1;
else:
indices_in = []; # 存放支持向量0<alpha<C的索引
for i in range(self.m):
if (self.alpha[i]>0 and self.alpha[i]<self.C):
indices_in.append(i);
for i in indices_in: # 对支持向量先进行选择
if (not self.judge_KKT(i)): # 如果这个样本不满足KKT,则作为第1个alpha,然后选择第2个alpha
self.E[i] = self.compute_E(i); # 第1个alpha样本的E值
j = self.select_second_alpha(i); # 选择第2个alpha
self.E[j] = self.compute_E(j); # 第2个E值
flag = self.update(i, j, self.E[i], self.E[j]);
if (flag == True):
parameterChanged += 1;
if (parameterChanged == 0): # 如果参数1个都没改变,则接下来进行整个训练集的遍历,如果参数变了,继续遍历支持向量
entire_flag = True;
iter_time += 1;
#打印迭代轮数,i值,该迭代轮数修改alpha数目
# print("iter: %d , pairs changed %d" % (iter_time, parameterChanged))
#全部计算结束后,重新遍历一遍alpha,查找里面的支持向量
for i in range(self.m):
#如果alpha>0,说明是支持向量
if (self.alpha[i] > 0 and self.alpha[i] < self.C):
#将支持向量的索引保存起来
self.supportVecIndex.append(i)
def sign(self, z):
"""
决策函数,返回类别
param
z: 预测值
"""
if (z >= 0):
return 1;
else:
return -1;
def show_trian_data(self):
"""
打印原始数据
"""
p = np.where(self.train_label==1)[0]; # 正样本索引
n = np.where(self.train_label==-1)[0]; # 负样本索引
fig, ax = plt.subplots(figsize=(8, 6));
ax.scatter(self.train_data[p, 0], self.train_data[p, 1], color='r');
ax.scatter(self.train_data[n, 0], self.train_data[n, 1], color='b');
plt.show();
def show_support_vector(self):
"""
打印支持向量
"""
p = np.array(self.supportVecIndex)[np.where(self.train_label[self.supportVecIndex]==1)[0]]; # 正样本索引
n = np.array(self.supportVecIndex)[np.where(self.train_label[self.supportVecIndex]==-1)[0]]; # 负样本索引
fig, ax = plt.subplots(figsize=(8, 6));
ax.scatter(self.train_data[p, 0], self.train_data[p, 1], color='r');
ax.scatter(self.train_data[n, 0], self.train_data[n, 1], color='b');
plt.show();
def show_boundary(self, flag):
"""
打印决策边界
param
flag: 为1则是画出数据集1的决策边界,2则是画出数据集2的决策边界。
因为数据集2有噪声样本,直接取最大最小值作为边界范围就太大了。
"""
if (flag == 1):
x_left, x_right = np.min(train_data[:, 0]) - 0.05, np.max(train_data[:, 0]) + 0.05; # 左右界
y_low, y_high = np.min(train_data[:, 1]) - 0.05, np.max(train_data[:, 1]) + 0.05; # 上下界
elif (flag == 2):
x_left, x_right = 0, 1.1; # 左右界
y_low, y_high = 0.38, 1; # 上下界
x = np.linspace(x_left, x_right, 500); # 按左右界生成序列
y = np.linspace(y_low, y_high, 500); # 同上
xx, yy = np.meshgrid(x, y); # 生成网格数据
xx = xx.reshape(-1, 1); # 拉长
yy = yy.reshape(-1, 1);
test_data = np.column_stack((xx, yy));
zz = []; # 存放预测类别
for sample in test_data:
zz.append(self.sign(self.compute_G_for_test(sample))); # 把预测类别添加到zz中
zz = np.array(zz);
p_sample = np.where(zz == 1)[0];
n_sample = np.where(zz == -1)[0];
fig, ax = plt.subplots(figsize=(8, 6));
ax.scatter(test_data[p_sample, 0], test_data[p_sample, 1], color='r');
ax.scatter(test_data[n_sample, 0], test_data[n_sample, 1], color='b');
plt.show();
"""
运行一个训练集实例
"""
path = 'dataset_2.mat'; # 需要修改为自己的路径
train_data, train_label = load_data(path):
svm = SVM(train_data, train_label, sigma = 0.1, C = 200);
svm.train();
svm.show_boundary(2); # 使用dataset_2时参数传2
参考文献
《统计学习方法》
博客:参考代码1
博客:参考代码2
知乎:零基础学SVM
B站:李航统计学习之SVM支持向量机+SMO算法数学推导