人工智能-作业2：例题程序复现

---

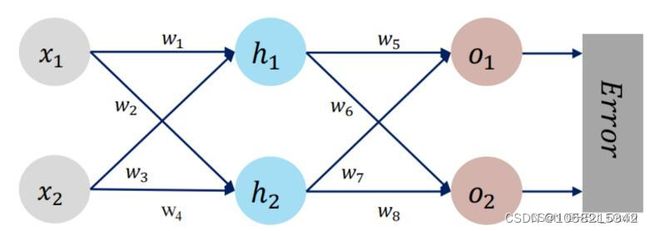
一、反向传播算法

反向传播算法是目前用来训练人工神经网络（Artificial Neural Network）的最常用且最有效的算法。是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。（误差的反向传播）

二、计算过程

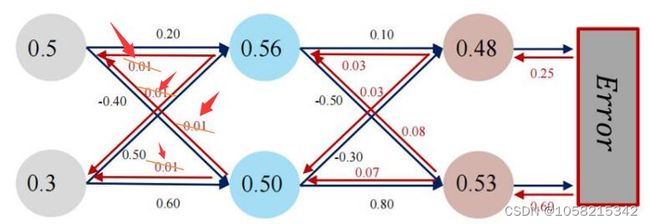
输入值：x1, x2 = 0.5，0.3
输出值：y1, y2 =0.23， -0.07
激活函数：sigmoid
损失函数：MSE
初始权值：0.2 -0.4 0.5 0.6 0.1 -0.5 -0.3 0.8

以计算w1 - w4 为例：


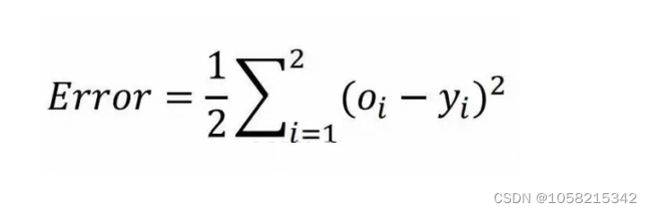
参数更新过程：

其中wi为原有步长，η为步长，δ为传递误差。

def update_w(w1,w2,w3,w4,...wn):
    step=5
    w1=w1-step*d_w1
    w2=w2-step*d_w2
    w3=w3-step*d_w3
    w4=w4-step*d_w4
          .
          .
          .
    wn=wn-step*d_wn
    return w1,w2,w3,w4,...wn
    

三、代码实现

import numpy as np
 
 
def sigmoid(z):
    a = 1 / (1 + np.exp(-z))
    return a
 
 
def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
    in_h1 = w1 * x1 + w3 * x2
    out_h1 = sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)
 
    in_o1 = w5 * out_h1 + w7 * out_h2
    out_o1 = sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)
 
    print("正向计算：o1 ,o2")
    print(round(out_o1, 5), round(out_o2, 5))
 
    error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
 
    print("损失函数：均方误差")
    print(round(error, 5))
 
    return out_o1, out_o2, out_h1, out_h2
 
 
def back_propagate(out_o1, out_o2, out_h1, out_h2):
    # 反向传播
    d_o1 = out_o1 - y1
    d_o2 = out_o2 - y2
    # print(round(d_o1, 2), round(d_o2, 2))
 
    d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
    d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
    # print(round(d_w5, 2), round(d_w7, 2))
    d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
    d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
    # print(round(d_w6, 2), round(d_w8, 2))
 
    d_w1 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x1
    d_w3 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x2
    # print(round(d_w1, 2), round(d_w3, 2))
 
    d_w2 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x1
    d_w4 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x2
    # print(round(d_w2, 2), round(d_w4, 2))
    print("反向传播：误差传给每个权值")
    print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
          round(d_w7, 5), round(d_w8, 5))
 
    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
 
 
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
    # 步长
    step = 5
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    return w1, w2, w3, w4, w5, w6, w7, w8
 
 
if __name__ == "__main__":
    w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
    x1, x2 = 0.5, 0.3
    y1, y2 = 0.23, -0.07
    print("=====输入值：x1, x2；真实输出值：y1, y2=====")
    print(x1, x2, y1, y2)
    print("=====更新前的权值=====")
    print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2))
 
    for i in range(1000):
        print("=====第" + str(i) + "轮=====")
        out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
        d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
        w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
 
    print("更新后的权值")
    print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2))

四、运行结果

=====输入值：x1, x2；真实输出值：y1, y2=====
0.5 0.3 0.23 -0.07
=====更新前的权值=====
0.2 -0.4 0.5 0.6 0.1 -0.5 -0.3 0.8
=====第0轮=====
正向计算：o1 ,o2
0.47695 0.5287
损失函数：均方误差
0.20971
反向传播：误差传给每个权值
0.01458 0.01304 0.00875 0.00782 0.03463 0.08387 0.03049 0.07384
=====第1轮=====
正向计算：o1 ,o2
0.43556 0.42626
损失函数：均方误差
0.14427
反向传播：误差传给每个权值
0.0117 0.01039 0.00702 0.00623 0.02779 0.06674 0.02446 0.05873
=====第2轮=====
正向计算：o1 ,o2
0.40429 0.35169
损失函数：均方误差
0.1041
反向传播：误差传给每个权值
0.00926 0.00818 0.00556 0.00491 0.02267 0.05193 0.01994 0.04568
=====第3轮=====
正向计算：o1 ,o2
0.38013 0.29988
损失函数：均方误差
0.07968
反向传播：误差传给每个权值
0.00749 0.00659 0.00449 0.00395 0.01883 0.04133 0.01656 0.03636
=====第4轮=====
正向计算：o1 ,o2
0.36101 0.26298
损失函数：均方误差
0.06402
反向传播：误差传给每个权值
0.00621 0.00545 0.00373 0.00327 0.01589 0.03394 0.01398 0.02986
...
...
...
=====第999轮=====
正向计算：o1 ,o2
0.23038 0.00954
损失函数：均方误差
0.00316
反向传播：误差传给每个权值
4e-05 3e-05 2e-05 2e-05 3e-05 0.00029 2e-05 0.00026
更新后的权值
-0.84 -1.3 -0.13 0.06 -1.55 -7.31 -1.75 -5.23

Process finished with exit code 0

五、参考资料

人工智能：模型与算法——中国MOOC
人工智能导论：模型与算法MOOC 8.3 误差后向传播(BP) 例题 编程验证
人工智能导论：模型与算法MOOC 8.3 误差后向传播(BP) 例题 【第三版】