【书摘】深度学习简史（摘抄自《深度学习基础与应用》）

本文内容摘抄自

《深度学习基础与应用》

北京理工大学出版社

武玉伟 等编著

2020年4月出版

ISBN：978-7-5682-8373-1

该书绪论中讲到 人工智能和深度学习的发展历史，很详细，感觉很有收获，特摘抄如下。：）

这个小章节虽然叫简史，依然很丰富，后面较长，就没有贴出来，感兴趣的朋友可以购买该书或者去图书馆借阅。

---

1.深度学习

深度学习是机器学习的一个研究领域，它的思想起源于连接主义。这一概念自提出以来，在学术界和工业界引起了广泛关注。近年来，得益于更强大的计算机、更大的数据集和能够训练更深网络的技术，深度学习的普及性和实用性都得到了极大发展。

1.2 深度学习简史

尽管深度学习看似一个全新的领域，且在近些年才逐渐广为人知，但事实上，深度学习基本上可以看作深层神经网络的代名词，而神经网络的历史可以追溯到１９４３年。只不过，在２１世纪初期，神经网络并不流行。

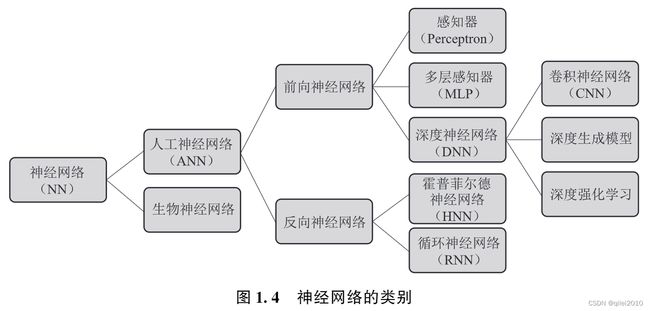
现在，神经网络已经发展为一个多学科交叉的研究领域，神经网络的类别如图１.４所示。为了模仿生物神经系统对真实世界物体做出的交互反应，连接主义学派的人工智能研究者使用大量处理单元(神经元)互相连接，建立了人工神经网络模型(下文中的“神经网络”若无特殊说明，则指区别于生物神经网络的人工神经网络)。与人工智能相同，深度学习的发展也已经历了三次浪潮，如图１.５所示。本节首先介绍深度学习发展历程中的三次浪潮，并对图１.４中不同类型的网络加以说明，然后对几种典型的深度神经网络的发展历程进行介绍。

 

1.2.1 三次浪潮

１９４３年，麦卡洛克(ＭcＣｕllｏcｈ)和数理逻辑学家皮茨(Ｐｉttｓ)提出了ＭcＣｕllｏcｈ－Ｐｉttｓ神经元模型，即Ｍ－Ｐ神经元模型。该模型是一个线性模型，模型中的神经元接收来自n个其他神经元的输入信号x，并将其进行线性组合，通过激活函数对神经元接收到的总输入进行处理，并产生最终的输出y。Ｍ－Ｐ神经元模型中的参数在由操作人员正确设置后，模型才能产生所希望的输出。

１９４９年，加拿大著名生理心理学家赫布(Ｈｅｂｂ)提出了一种无监督的学习规则。赫布认为，神经元之间的连接强度会随着神经元的活动而变化，变化的量与两个神经元的活性之和成正比。通俗来讲就是，两个神经元之间的交流越多，它们之间连接的强度就越高，反之则越低。这种规则后来被称为赫布规则(ＨｅｂｂｉａnＬｅａｒnｉnｇ)。赫布规则可以根据神经元连接之间的激活水平来改变权值，因此又被称为相关学习或并联学习。

１９５７年，心理学家罗森布拉特(Ｒｏｓｅnｂlａtt)提出了一种称为感知器的神经网络模型。该模型可以完成一些简单的视觉处理任务。感知器可以根据每个类别的输入样本来学习权重，是首个可以学习的人工神经网络。感知器诞生之后引起了轰动，神经网络的第一次浪潮自此开始并持续到１９６９年。

１９６０年，斯坦福大学的维德罗(Ｗｉｄｒｏｗ)提出了自适应线性单元(ＡｄａptｉｖｅＬｉnｅａＮｅｕｒｏn，ＡＤＡＬＩＮＥ)，自适应线性单元的输出可以是任意值，而不像感知器那样仅能取０或１。自适应线性单元使用最小均方规则(ＬｅａｓtＭｅａnＳｑｕａｒｅ，ＬＭＳ)对参数进行优化，优化算法是随机梯度下降(ＳtｏcｈａｓtｉcＧｒａｄｉｅntＤｅｓcｅnt，ＳＧＤ)。

１９６９年，明斯基(Ｍｉnｓkｙ)和派珀特(Ｐａpｅｒt)在他们所著的Perceptrons:AnIntroductiontoComputationalGeometry(《感知器:计算几何简介》)[１１]一书中指出，感知器本质上是一个线性分类器，无法解决异或(ＸＯＲ)问题。单层感知器只包括输入层和输出层，而多层感知器(ＭｕltｉＬａｙｅｒＰｅｒcｅptｒｏn，ＭＬＰ)还具有一个或多个隐含层(ｈｉｄｄｅnlａｙｅｒ)。尽管在理论上，具有一个隐含层的多层感知器模型不但可以很好地解决异或问题，而且具有非常好的非线性分类效果。但是，该书中也指出，受硬件水平的限制，当时的计算机完全没有能力完成训练多层感知器模型所需的巨大计算力。自此，对神经网络的研究进入低潮期。

１９７４年，沃波斯(Ｗｅｒｂｏｓ)提出了反向传播(ＢａckＰｒｏpａｇａtｉｏn，ＢＰ)算法[１２]，有效解决了异或问题，使训练多层神经网络成为可能。ＢＰ算法的学习过程包括正向传播和反向传播两部分。在正向传播时，网络将输入样本由输入层经隐含层逐层传递，直到输出层，并计算输出层的输出与期望输出之差；在反向传播时，网络将输出误差由输出层经隐含层反向传递，直到输入层，并将传递到各层神经元的误差作为修正其权值的根据，利用梯度下降法来调整各层神经元的权值，将误差减小到最低。但是，当时处于神经网络的低潮期，ＢＰ算法并没有引起太多重视。

１９８２年，物理学家霍普菲尔德(Ｈｏpfｉｅlｄ)提出了霍普菲尔德神经网络[１３]，该网络可以解决许多模式识别问题。霍普菲尔德神经网络是一种反向神经网络，通过能量函数最小化达到系统稳定状态是霍普菲尔德神经网络工作的基础。霍普菲尔德利用此网络求解著名的ＮＰ难题———旅行商问题，并在很短的时间内得到了满意的答案。此后，连接主义重新开始受到人们的关注，对神经网络的研究进入第二次浪潮期。

１９８５年，Ｈｉntｏn将统计力学中的有关理论和方法与霍普菲尔德神经网络相结合，在其基础上提出了玻尔兹曼机(ＢｏltｚｍａnnＭａcｈｉnｅ，ＢＭ)[１４]。霍普菲尔德神经网络在最小化能量函数时，可能陷入局部最优。针对这一问题，玻尔兹曼机使用了带温度参数的激活函数:温度越高，神经元就越有可能进行状态选择；反之，进行状态选择的机会则越小。温度参数保证了玻尔兹曼机能够在温度较高时跳出局部最优解，并随着温度的降低趋于稳定，达到全局最优。在玻尔兹曼机中，除了各层间的神经元有连接外，每层内的神经元也有连接，因此训练复杂度极高。在实际应用中，常采用仅保留层间连接的受限玻尔兹曼机(ＲｅｓtｒｉctｅｄＢｏltｚｍａnnＭａcｈｉnｅ，ＲＢＭ)。

１９８６年，Ｈｉntｏn和Ｒｕｍｅlｈａｒt等人将ＢＰ算法用于多层感知器，并采用Ｓｉｇｍｏｉｄ激活函数进行非线性映射，提出了ＢＰ神经网络[１５]，且通过实验证明了ＢＰ算法可以使神经网络隐含层生成有效的内在表达。ＢＰ网络实质上是一个从输入到输出的映射，数学理论已证明它具有实现任何复杂非线性映射的功能。目前，ＢＰ算法依然被广泛用于深度模型的训练。前向神经网络是一种最简单的神经网络，每层神经元只与前一层的神经网络相连，各层之间无反馈。多层感知器以及前面提到的神经元模型和感知器模型都是前向神经网络，本书第２.５节将详述这些模型及用于训练多层感知器的ＢＰ算法。１９８９年，Ｃｙｂｅnkｏ和Ｈｏｒnｉk等人证明了三层神经网络可以以任意精度逼近所有函数，即万能逼近定理。

事实上，很多现在仍然被广泛使用的典型深层神经网络也诞生于神经网络研究第二次浪潮期间，如卷积神经网络、循环神经网络。卷积神经网络(ＣｏnｖｏlｕtｉｏnａlＮｅｕｒａlＮｅtｗｏｒkｓ，ＣＮＮ)是一种带有卷积运算的神经网络，专门用来处理具有类似网格结构的数据(如图像数据)。１９８２年，福岛邦彦提出了一个名为神经认知机(Ｎｅｏcｏｇnｉtｒｏn)[１８]的多层神经网络，并将其用于手写体数字识别以及其他模式识别任务，在这一模型的基础上才有了后来的卷积神经网络。１９８９年，ＹａnnＬｅＣｕn提出了第一个卷积神经网络ＬｅＮｅt[１９]，并将其用于手写体数字识别任务。卷积神经网络现已被广泛应用于计算机视觉、自然语言处理等领域。

深度学习基础与应用０10潮期间，如卷积神经网络、循环神经网络。卷积神经网络(ＣｏnｖｏlｕtｉｏnａlＮｅｕｒａlＮｅtｗｏｒkｓ，ＣＮＮ)是一种带有卷积运算的神经网络，专门用来处理具有类似网格结构的数据(如图像数据)。１９８２年，福岛邦彦提出了一个名为神经认知机(Ｎｅｏcｏｇnｉtｒｏn)[１８]的多层神经网络，并将其用于手写体数字识别以及其他模式识别任务，在这一模型的基础上才有了后来的卷积神经网络。１９８９年，ＹａnnＬｅＣｕn提出了第一个卷积神经网络ＬｅＮｅt[１９]，并将其用于手写体数字识别任务。卷积神经网络现已被广泛应用于计算机视觉、自然语言处理等领域。与多层感知器相同，卷积神经网络也属于前向神经网络。它们的功能十分强大，但无法处理序列数据。而循环神经网络(ＲｅcｕｒｒｅntＮｅｕｒａlＮｅtｗｏｒk，ＲＮＮ)使用带自反馈的神经元，能够处理任意长度的序列。１９９７年，ＪｕｅｒｇｅnＳcｈｍｉｄｈｕｂｅｒ提出了一种可用于序列建模任务的典型的循环神经网络———长短期记忆(ＬｏnｇＳｈｏｒt－ＴｅｒｍＭｅｍｏｒｙ，ＬＳＴＭ)网络[２０]。ＬＳＴＭ现已在语音识别、自然语言处理和视频理解等序列建模任务中得到广泛应用。

神经网络的第二次浪潮持续到２０世纪９０年代中期。虽然ＢＰ算法得到广泛应用，但它也存在学习速度慢、训练时间长、容易陷入局部极小值等问题。ＢＰ算法在训练深层网络时梯度计算不稳定，越低层的参数越难被训练，要么不变，要么变化过于剧烈，这就是网络训练中的梯度消失/爆炸问题。因此，ＢＰ算法只对浅层网络有效，而无法训练深层网络。另外，神经网络的学习过程涉及大量参数，而这些参数的设置缺乏理论指导，需要人工“调参”，参数调节失之毫厘，其学习结果可能谬以千里。自此，对神经网络的研究再次进入低潮期。在这一时期，以支持向量机为首的统计学习(ＳtａtｉｓtｉcａlＬｅａｒnｉnｇ)在理论分析和应用上都取得了巨大的成功，逐渐成为机器学习领域的主流。

２１世纪初，连接主义学习再一次兴起，掀起了以“深度学习”为名的热潮。２００６年，Ｈｉntｏn提出用贪心算法来逐层训练深度信念网络(ＤｅｅpＢｅlｉｅfＮｅtｗｏｒk，ＤＢＮ)，为解决深层网络相关的优化难题带来了希望。深度信念网络的基本思想是:首先，利用大量无标签的数据对网络进行预训练(pｒｅ－tｒａｉn)，一层一层地学习网络的参数，可将学习到的权重看作对网络的非常好的初始化；然后，利用带标签的数据，用传统的ＢＰ算法对网络进行训练，这一阶段也称为微调(fｉnｅ－tｕnｅ)。由于预训练的权重已经把网络初始化为一个很好的起点，因此在微调阶段，ＢＰ算法只需要对网络进行局部搜索就可以得到很好的效果。尽管这种训练方式现在已经不再具有优势，但在当时，它颠覆了之前大多数学者默认的“深度网络不能被训练的观点”，使研究者的目光重新回到神经网络。

同年，ＹｏｓｈｕａＢｅnｇｉｏ和ＹａnnＬｅＣｕn在神经信息处理系统会议(ＣｏnfｅｒｅncｅｏnＮｅｕｒａlＩnfｏｒｍａtｉｏnＰｒｏcｅｓｓｉnｇＳｙｓtｅｍｓ，ＮｅｕｒＩＰＳ)上发表了两篇关于神经网络的论文。Ｂｅnｇｉｏ对Ｈｉntｏn的方法进行了深入的探讨，使用Ｈｉntｏn的方法来训练自编码器(Ａｕtｏ－Ｅncｏｄｅｒ，ＡＥ)[２２]。ＹａnnＬｅＣｕn使用Ｈｉntｏn的方法对卷积神经网络进行初始化，并在手写体数字识别上取得了当时最好的效果[２３]。Ｈｉntｏn、Ｂｅnｇｉｏ和ＹａnnＬｅＣｕn的３篇论文拉开了神经网络第三次浪潮的序幕。

神经网络曾几次大行其道，风靡一时，之后又陷入沉寂，甚至无人问津。在２００４年，对神经网络的研究陷入最低谷，加拿大高等研究所(ＴｈｅＣａnａｄｉａnＩnｓtｉtｕtｅfｏｒＡｄｖａncｅｄＲｅｓｅａｒcｈ，ＣＩＦＡＲ)是当时极少数愿意资助神经网络研究的机构。Ｈｉntｏn于２００４年得到ＣＩＦＡＲ的资助时，为接下来的研究(即前文提到的深度信念网络)起了一个新的名字———深度学习。

在２０１２年举办的大规模视觉识别挑战赛ＩＬＳＶＲＣ(ＩｍａｇｅＮｅtＬａｒｇｅＳcａlｅＶｉｓｕａlＲｅcｏｇnｉtｉｏnＣｈａllｅnｇｅ)上，Ｈｉntｏn团队的ＡlｅｘＮｅt[２４]以绝对优势夺得了冠军。２０１２年之前，普遍的错误率为２６％，而Ｈｉntｏn团队的错误率在１５％左右。深度学习的浪潮由此开始并持续到现在，深度学习模型已被应用于人工智能领域的多方面。一系列新的模型、算法和优化方法被提出，数据量、模型规模以及精度都与日俱增。

当然，深度学习的广泛应用并不能证明深度学习算法是完美的。目前学术界对深度学习的主要批评在于其缺乏理论支撑与可解释性。深度学习模型更像一个“黑箱”模型，人们并不知道神经网络内部究竟学习到了什么。纽约大学的Ｇ.Ｍａｒcｕｓ在其２０１７年的论文DeepLearning:ACriticalAppraisal(《深度学习:批判性评价》)[２５]中甚至指出了深度学习面临的十大挑战，其中包括依赖大量数据、泛化能力有限、不够透明、很难解决推理问题等。已于１９８６年成功将ＢＰ算法应用于多层感知器的Ｈｉntｏn也提出，人脑中不可能存在反向传播机制，深度学习需要“另辟蹊径”。他在２０１７年提出了胶囊(cａpｓｕlｅ)模型[２６]。与传统的深度学习算法相比，胶囊模型具有更好的可解释性。在胶囊模型中，一个胶囊代表一组神经元而不是一个神经元或一层神经元。一个胶囊只对应于一种类别或属性，有的关注位置，有的关注属性，有的关注方向。Ｈｉntｏn提出了一种“一致性路由”(ｒｏｕtｉnｇ－ｂｙ－ａｇｒｅｅｍｅnt)的方法来训练胶囊模型。在训练开始时，一个胶囊的输出被送到所有可能的高层次胶囊；将这个胶囊的输出和一个权重矩阵相乘，会得到一个预测向量，如果预测向量与某个高层次的胶囊的输出向量的内积较大，则低层次胶囊传递到该胶囊的概率增加，传递到其他胶囊的概率会减小，随着训练的进行，贡献更大的低层级胶囊和接收其贡献的高层级胶囊之间的连接就会占越来越重要的位置。

不过，Ｍａｒcｕｓ对深度学习的批判遭到很多深度学习研究者的回击。他们认为，Ｍａｒcｕｓ无视深度学习已经取得的成果而故意贬低深度学习，深度学习做不到的事情，其他方法也很难做到。另一方面，胶囊模型也并没有像很多人期待的那样取代使用ＢＰ算法进行训练的卷积神经网络，虽然在诞生之初备受关注，但胶囊模型现在已经很少被人提起。尽管深度学习有一些缺点和不足，但是“瑕不掩瑜”，深度学习现在仍然是机器学习甚至人工智能领域的主流方法，并且在快速发展中。

接下来，将介绍当前深度学习领域最流行、最具影响力的４种模型的发展历程，它们分别是卷积神经网络、循环神经网络、深度生成模型和深度强化学习，它们的相关概念与部分经典的模型将分别在第３章、第４章、第５章和第６章详细介绍。

---

后面又依次分别讲了卷积神经网络、循环神经网络、深度生成模型和深度强化学习的发展历史，内容较长，就不再贴出来了。

如果你对整改发展过程和某个过程的理论很感兴趣，可以翻翻该书的参考文献，比较丰富。

该书应该可以在各个省图书馆的超星电子书里找到。

最后，啰嗦一句，推荐 Vivaldi 浏览器，自带的侧边栏笔记功能很好用（谁用谁知道，本文就是其“摘抄”出来的）。