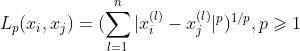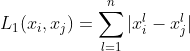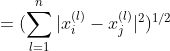统计学习方法——k近邻法

目录

统计学习方法——k近邻法

算法描述

k近邻模型

k近邻法实现:kd树

构造平衡kd树

搜索kd树

Reference

 

统计学习方法——k近邻法

 

算法描述

  k近邻算法是一种基本分类与回归方法。李航老师的书中只讨论了分类问题。

  k近邻算法简单直观：

                             （1）给定一个训练数据集

                             （2）对于新的输入实例，在训练数据集中找到与该实例最邻近的k个实例

                             （3）这k个实例多数属于某个类，就将该输入实例分到这个类中

 

算法3.1(k近邻法)

  输入：训练数据集

                                            

  其中，为实例的特征向量，为实例的类别，实例特征向量;

  输出：实例所属的类y

  （1）根据给定的距离度量，在训练集T中找出与x最邻近的k个点，涵盖这k个点x的邻域记为

    (2)在中根据分类决策规则（如多数表决）决定x的类别y

                                   

  I为指示函数，当时I为1，否则为0，I值最大，求出的也就是新的输入实例类别

  k=1时，称为最近邻算法，最近邻算法将训练数据集中与x最邻近的点的类作为x的类

k近邻模型

k近邻模型三要素=距离度量+k值选择+分类决策规划

距离度量

设特征空间X时n为实数向量空间，

的距离定义为  

                                                       

p=1,称为曼哈顿距离(Manhattan distance)：

                   

p=2,称为欧氏距离(Euclidean distance)：

                 

                                 

 

 k值选择

选择较小的k值，“学习”的近似误差会减小，如果过小，整体模型会复杂，容易发生过拟合

选择较大的k值，会减小学习的估计误差，如果过大近似误差会增大，因为与输入实例较远

的训练实例也会对预测起作用，使预测发生错误

 

分类决策规则

多数表决法：

误分类概率：

    

分对的和分错的加起来为k个

要使误分类率即经验风险最小，就要使最大，所以多数表决规则等价于经验风险最小化

 

k近邻法实现:kd树

kd(k dimensional tree)是存储k维空间数据的树结构，这个k与k近邻算法中的k含义不同。

k近邻法最简单的实现方法是线性扫描，要计算输入实例与每个训练实例的距离，当训练集大时，

计算非常耗时。为提高效率采用特殊的结构存储训练结构，如kd树。

构造平衡kd树

输入：k维空间数据集,其中

输出：kd树

（1）开始：构造根结点，根结点对应于包含T的k维空间的超矩形区域。

以为坐标轴，以T中所有实例的坐标中位数为切分点（若总数为双数则取中间两数平均值），

将根节点对应的超矩形区域切分为两个子区域，切分由通过切分点并与坐标轴垂直的超平面实现。

由根节点生成深度为1的左右子结点，左子节点对应小于的子区域，右边大于。

将落在切分超平面上的实例点保存在根节点。

（2）重复：对深度为j的结点，选择为切分坐标轴，（这里注意根结点是第0层）

然后重复（1），直至没有实例。

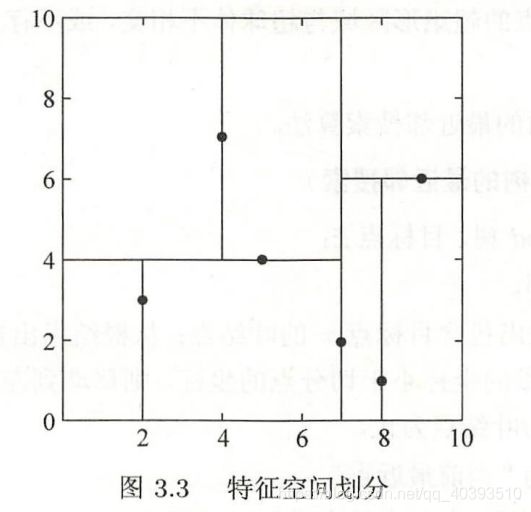
例3.2：给定一个二维空间的数据集：

构造一个平衡kd树。

解：第一步：选轴：2，4，5，7，8，9，中位数为6，但6上没有数据点，所有选,

以平面将空间分为左右两个子矩形

第二步：

左边以分为2个子矩形，右边以分为2个子矩形

第三步：

这层都是叶子结点

 

搜索kd树

输入：已构造的kd树，目标点x

输出：x的最近邻

（1）在kd树中找出包含目标点x的叶结点：从根结点出发，递归的向下访问，

若目标点x当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，

直到子结点为叶结点为止。

（2）以叶结点为当前最近点，递归的向上回退，在每个结点进行以下操作：

        （a）：如果该结点保存的实例点比当前最近点到目标点的距离更近，更新该实例点为“当前最近点”。

        （b）：当前最近点一定存在于该节点的一个子结点对应的区域。检查该结点的另一个子节点对应的区域是否与

                    以目标点为球心、以目标点到“当前最近点”间的距离为半径的超球体相交。如果相交，移动到另一个子结点

                  ，递归进行最近邻搜索。若不相交，向上回退。

（3）当回退到根节点时，搜索结束，最终的“当前最近点”为x的最近邻点。

 

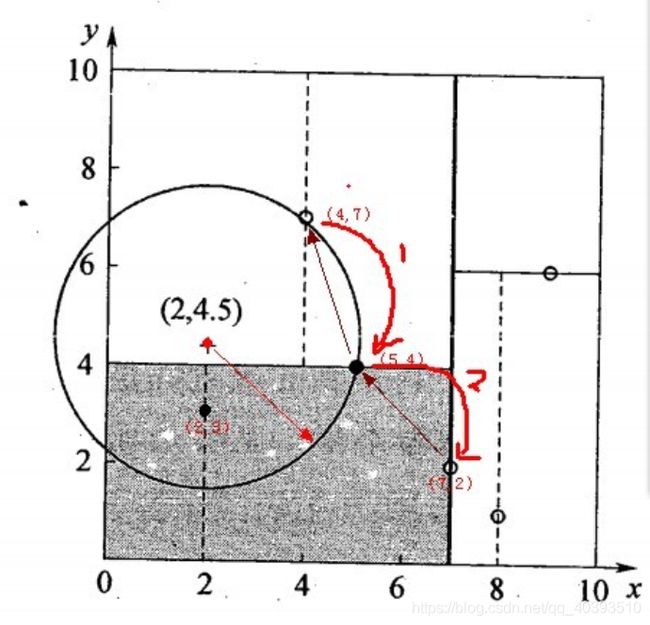
例3.3：以例3.2的数据集构造kd树，并找出(2, 4.5)的最近邻点。

第一步：按照（1）向下访问，顺序为

第二步：因为

                     

                     更新(5.4)为当前最近点

第二步：根据（b），检查是否与圆交割，

由下图可见是相交的。将(2, 3)结点加入搜索路径。

因为，所以更新(2, 3)为“当前最近点”

，回退到(7, 2)，并没有和相交，所以最终最近点为(2, 3)

 

Reference:（1）统计学习方法 李航

---

（2）kd树搜索（k邻近法）_Barry-njr的博客-CSDN博客_kd树搜索