数学建模 线性规划模型基本原理

线性规划问题

例1.1

可行解&可行域

matlab标准形式及软件求解

标准形式:
C称为价值向量

如果是求max,加一个负号-c^T
如果是求Ax>=b,加一个负号-Ax<=b

使用matlab求线性规划例题

求解的是最大值:加上负号
y是求解的最优解

zeros()使用:
zeros(n)：生成n×n全零阵
zeros(m,n)或者zeros([m n])：生成m×n全零阵
zeros(size(A))：生成与矩阵A相同大小的全零阵

所以zeros(3,1):生成3行1列的全零阵,3个x,1个y

非线性函数转线性函数

任何1个数x可以通过两个数相加来得到,|x|可以通过两个数相减来得到

建模实战–投资的收益和风险

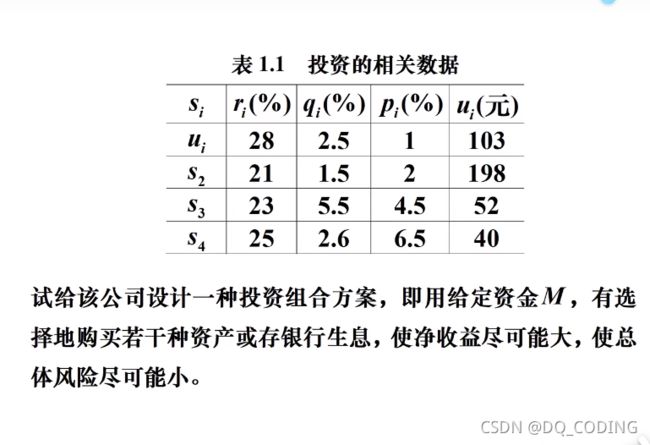
问题提出:

ui:最低购买量
第一行的ui是s1,这里没有列出存入银行的情况

符号规定

购买资产使用资金计量,而不是数量
s0存入银行,s1-s4投资资产
x0代表投资银行的资金,x1-x4代表投资资产的资金

基本假设

如果资产之间不独立就会彼此扰动

模型的分析与建立

购买的交易费很多,直接忽略uixi,用pixi计算

目标函数与约束条件

minmax{qi,xi}:总体风险=所有风险中最大的,同时要总体风险最小
总资金:M=购买资产花费的费率xi*pi+投资项目的资金xi

模型建立-多目标规划转单目标线性规划

模型一:固定风险水平,优化收益

qixi/M<=a:风险率投资资产金额/总金额<=a风险界限

求解:
带入数据:
1)因为a不知道,所以要逐个搜索
2)之前设置了M=1
3)因为投资银行x0,没有风险q0=0,没有交易费p0=0,所以存入银行的花费就是x0
4)f=(ri-pi) 收益,x0的收益为存款利率r0=0.05

matlab程序:
1)因为是要求最大的收益,所以c加上负号:c是投资资金x0-x5
2)zeros(4,1)生成4行1列的矩阵(4个x1-x4,一个y),A是计算风险
3)Q=-Q,求最大收益max
4)ones():
ones的作用是产生全1矩阵
ones(N)是产生一个NN的全1矩阵
ones(M,N)产生一个M*N的矩阵
ones(size(A))产生的矩阵应该是与A大小相同的全1矩阵

所以,aones(4,1):产生一个41的全a矩阵

5)plot():
使用plot绘制二维图像

plot(X, Y, LineSpec)
其中X由所有输入点坐标的x值组成，Y是由与X中包含的x对应的y所组成的向量。LineSpec是用户指定的绘图样式

所以,plot(a,Q,’*k’)表示:
函数图形用黑色颜色和星号符号来表示a和Q的函数曲线关系。
这里，plot是绘图函数，a和Q是一组数据，k是黑色颜色的代号，星号在图形中表示a和Q的对应值。

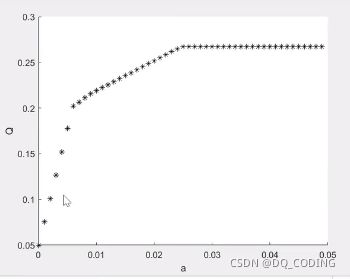
matlab结果:
在不同风险度的情况下,收益率都是不一样的,但总体风险越大,收益越高
如果可接受的风险度在0.006,为最佳的收益;如果可接受的风险度比较低,往往能获得一个更好的更高效的收益;如果可接受的风险度标记高,也建议不要超过0.025,这也会达到一个比较理想的效果,比风险度更高的时候收益更好

结论:

模型二:固定盈利水平,极小化风险

让盈利不小于k(最低的收益保证)

模型三:投资偏好

一般s设为0.5,如果s设为0.2,比较看重收益(1-s)
(总风险-总收益)min=赔的钱
或
(总收益-总风险)max=赚的钱