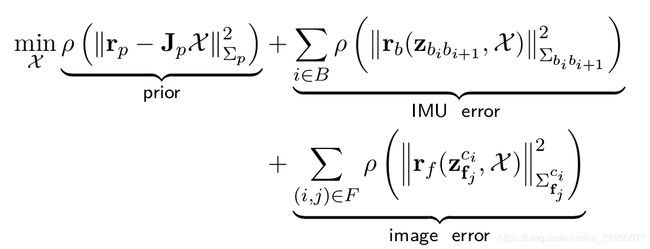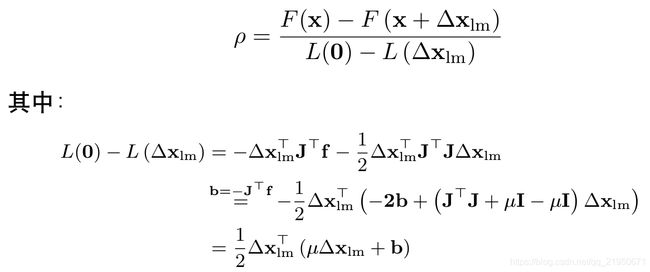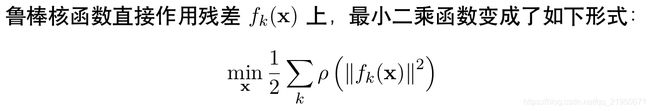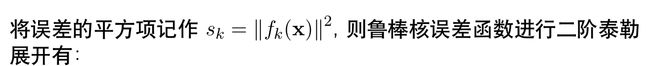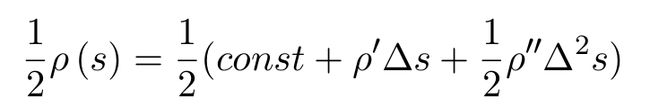【视觉SLAM十四讲源码解读】3D空间点和2D特征点求位姿并用高斯牛顿和G2O优化
文章目录
-
- 运行结果
- 算法解析
- 最小二乘法有什么用？最速下降法有什么用？
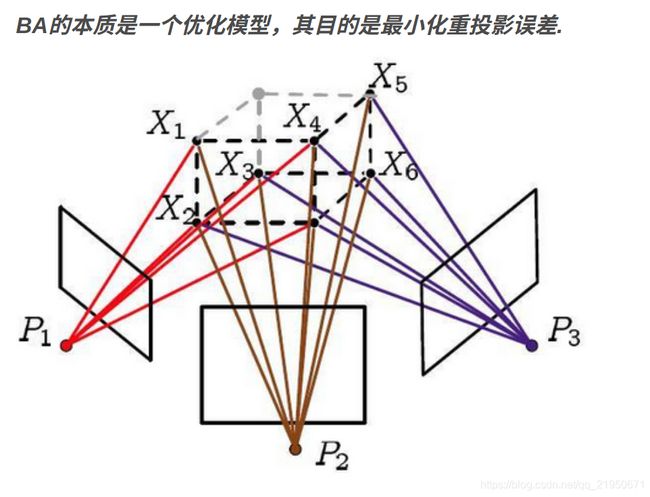
- 视觉 SLAM 里的 Bundle Adjustment 问题
- 源码解读
运行结果
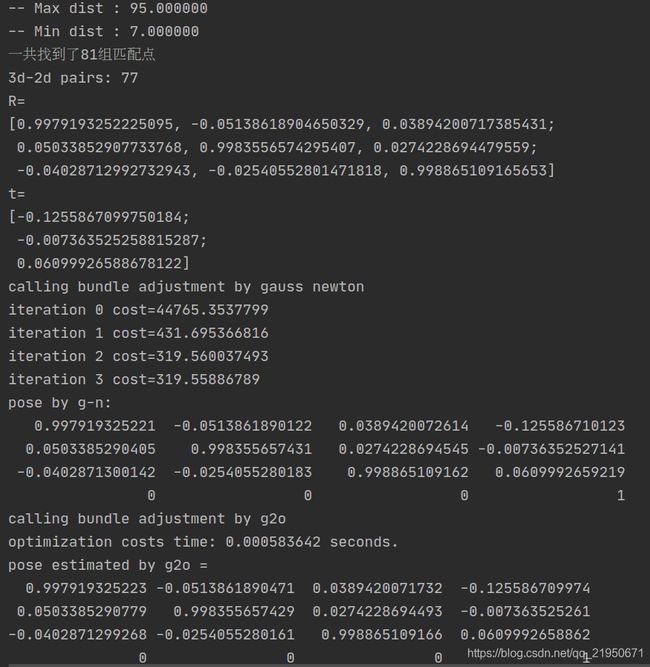
./pose_estimation_3d2d
算法解析
投影模型和 BA 代价函数
重投影误差示意图
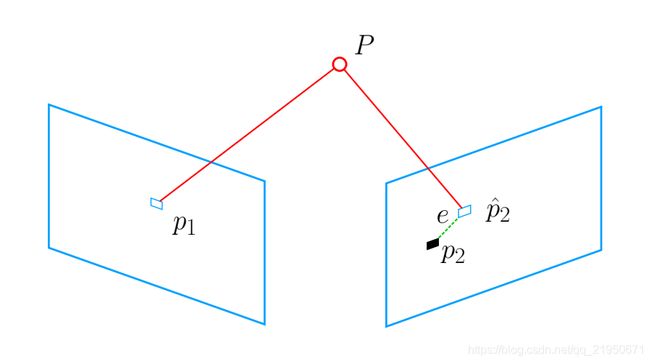当相机为双目，RGB-D时，或者通过某种方法获得了距离信息，那么问题就是根据两组3D点估计运动，通常用ICP解决。
如果一组为3D点，一组为2D，即，我们求得了一些3D点和它们在相机的投影位置，也能估计相机的运动，该问题通过pnp求解。
PnP 的 Bundle Adjustment 的图优化表示
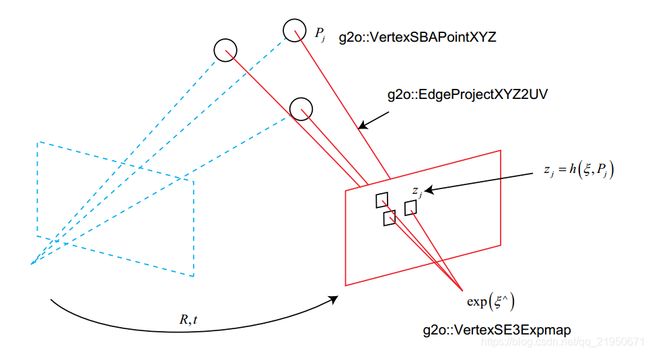
双目或RGBD的视觉里程计中使用PnP估计相机运动。
PnP包括的算法：
用三对点估计位姿P3P
输入：３对3D-2D匹配点
3D点世界坐标系的坐标
2D 相机成像平面的投影
一旦3D点在相机坐标系下面的坐标能够算出来，我们就得到了3D-3D的对应点，
把PnP问题转换成了ICP问题。
直接线性变换 DLT
EPnP
UPnP
关于重投影误差
最小二乘法有什么用？最速下降法有什么用？
最小二乘法有什么用？
什么是拟合？
你有一堆数据点，我有一个函数，但是这个函数的很多参数是未知的，我只知道你的这些数据点都在我的函数上，因此我可以用你的数据点来求我的函数的未知参数。
神经网络的输入就是一堆数据点， 神经网络里面的参数就是函数的系数，神经网络就是函数。
当我们用一组数据去求函数的参数的时候，就认为参数的最好的这样不科学。
当我们把所有数据一个个去求函数的参数的时候，问题来了怎么去评价其中一组参数值得好坏呢？
方法是，随机选择一组系数，输入数据，计算输出值， 并和真实值对比，选择接近程度最近的的一组系数。
但是这样计算起来的还是麻烦，在挑选系数的方法上就衍生出了一系列的方法，我们知道
其实我们从图中不难看出，左侧，y随着x增加时，导数为正，因此导数的方向我们可以定义为指向x正方向，x与导数同向也就是x也逐渐增加时，函数是增大的。右侧，y随x增加而较小，导数为负，我们这里还定义导数的方向此时指向x负半轴，因此x沿负方向减小时，函数值是逐渐增大的，这里需要记住和注意，沿着导数方向，我们的函数值是逐渐增大的。
解释清了上面一点，我们就可以再升几维，在一维时我们的方向只能谈论左右，而上升到二维时，我们的方向就成了平面的360度了，此时就引出了梯度，下图是二维梯度
可以将预测值和真实值先组成一个函数，然后让这个函数的值逐渐降低，就是求导数，导数的值是负数的时候 函数就是下降的，最速下降就是导数是负数的方向。
通过数据点求函数的参数，没有解析解能够直接代入数据求得参数，而是通过一点一点的摸索尝试，最终得到最小误差也就是最好拟合
最具有代表性的就是暴风法，把所有可能的结果都带进去，找到最好的拟合。然后聪明的人类不想这么鲁莽，并且这么无目的地寻找，于是人们开始研究参数向什么方向迭代是最好的，于是便出现了梯度方向等一系列方法。
最小二乘法天生就是用来求拟合的，看函数和数据点的逼近关系。
它通过最小化误差的平方和寻找数据的最佳函数匹配进行求解。
视觉 SLAM 里的 Bundle Adjustment 问题
已知
• 状态量初始值:特征点的三维坐标,
相机的位姿。
• 系统测量值:特征点在不同图像上的
图像坐标。
问题:如何估计状态量的最优值?
符号定义:
• q:旋转四元数
构建误差函数,利用最小二乘得到状态量
的最优估计:
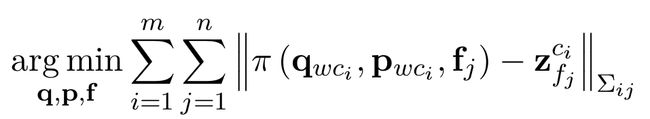
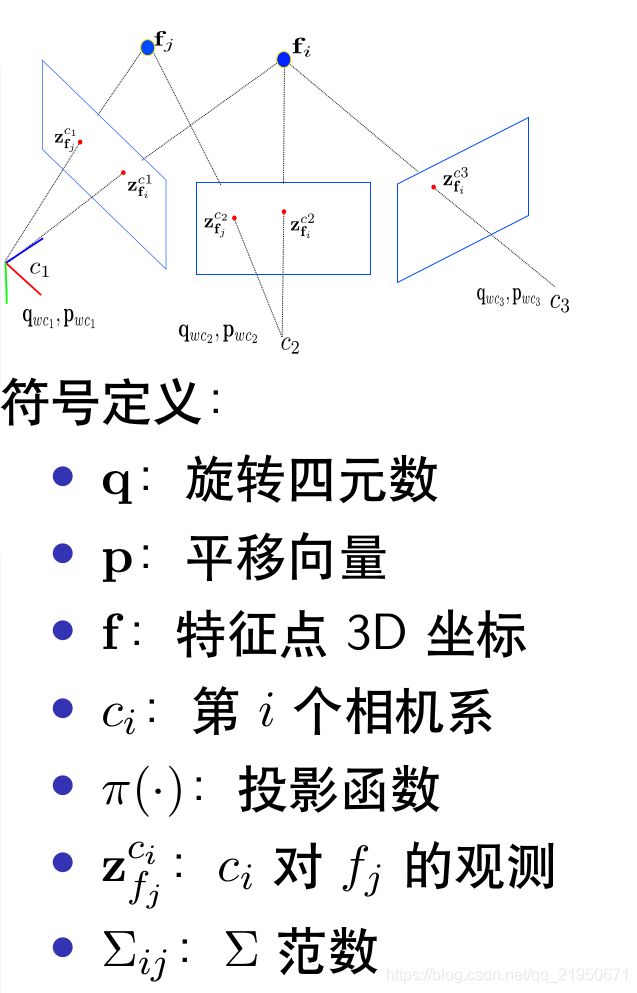
VIO 信息融合问题
基于滑动窗口的 VIO Bundle Adjustment
最小二乘基础概念
损失函数泰勒展开
损失函数泰勒展开性质
求解法
直接求解:线性最小二乘。
迭代下降法:适用于线性和非线性最小二乘。
迭代下降法求解:下降法
最速下降法和牛顿法
最速下降法: 适用于迭代的开始阶段
牛顿法:适用于最优值附近
阻尼法
非线性最小二乘
非线性最小二乘
残差函数 f (x) 为非线性函数,对其一阶泰勒近似有:
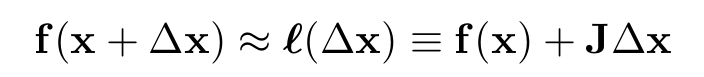
请特别注意,这里的 J 是残差函数 f 的雅克比矩阵。代入损失函数:
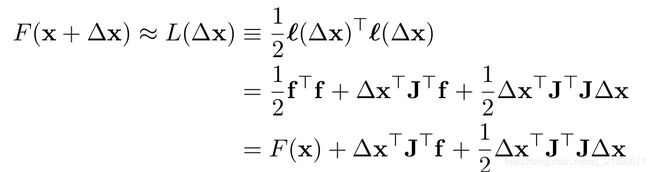令公式的一阶导等于 0,得到:
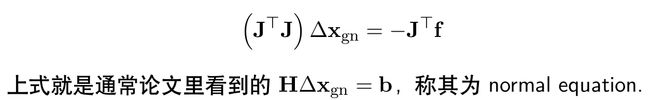
高斯牛顿法进行了改进,求解过程中引入了阻尼因子:
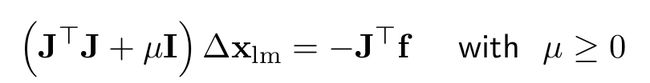阻尼因子的作用
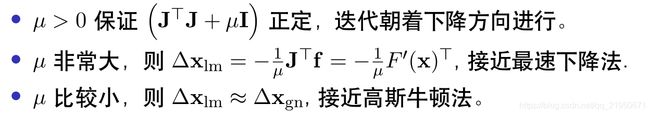阻尼因子初始值的选取
阻尼因子 μ 的更新策略
定性分析,直观感受阻尼因子的更新:
定量分析,阻尼因子更新策略通过比例因子来确定的:
Marquardt 策略
有最速下降法、Newton 法、GaussNewton(GN)法、Levenberg-Marquardt(LM)算法等。
https://blog.csdn.net/a6333230/article/details/83304098
图优化理论
图优化，就是把优化问题表现成图(Graph)的一种方式，一个图由若干顶点(Vertex)以及连接这些顶点的边(Edge)构成。
用顶点表示优化变量，用边表示误差项。
对任意一个上述形式的非线性最小二乘问题，我们可以构建与之对应的一个图。
g2o默认使用四元数和平移向量表达位姿。
//选择优化方法
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,3> > SlamBlockSolver;
//选择线性方程求解LinearSolver求解器CSparse，每个误差项优化变量维度6为pose的维度，误差值维度为3表示landmark的维度
typedef g2o::LinearSolverCSparse< SlamBlockSolver::PoseMatrixType > SlamLinearSolver;
//初始化求解器
std::unique_ptr linearSolver ( new SlamLinearSolver());
linearSolver->setBlockOrdering( false );
//选择一个块求解器blockSolver包含线性求解器之所以包含是因为块求解器会构建好线性求解器所需要的矩阵块（也就是H和b）
std::unique_ptr blockSolver ( new SlamBlockSolver ( std::move(linearSolver)));
//选择一个迭代策略OptimizationAlgorithmL：这里选择的是LM
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::move(blockSolver));
//得到一个图模型globalOptimizer
g2o::SparseOptimizer globalOptimizer;
//设置求解器
globalOptimizer.setAlgorithm( solver );
//不要输出调试信息
globalOptimizer.setVerbose( false );
// 向globalOptimizer增加第一个顶点
g2o::VertexSE3* v = new g2o::VertexSE3();
v->setId( currIndex );
//估计为单位矩阵
v->setEstimate( Eigen::Isometry3d::Identity() );
//第一个顶点固定，不用优化
v->setFixed( true );
globalOptimizer.addVertex( v );
//向图中增加顶点，顶点只需设定id即可
g2o::VertexSE3 *v = new g2o::VertexSE3();
v->setId( currIndex );
v->setEstimate( Eigen::Isometry3d::Identity() );
globalOptimizer.addVertex(v);
// 向图中增加边
g2o::EdgeSE3* edge = new g2o::EdgeSE3();
// 连接此边的两个顶点id
edge->vertices() [0] = globalOptimizer.vertex( lastIndex );
edge->vertices() [1] = globalOptimizer.vertex( currIndex );
//每条边设定一个信息矩阵（协方差矩阵之逆），作为不确定性的度量：信息矩阵 Ω 是协方差矩阵的逆，是一个对称矩阵。
//它的每个元素可以看成我们对ei,ej这个误差项相关性的一个预计。最简单的是把Ω设成对角矩阵，对角阵元素的大小表明我们对此项误差的重视程度。
//例如：你觉得帧间匹配精度在0.1m，那么把信息矩阵设成100的对角阵即可。
Eigen::Matrix<double, 6, 6> information = Eigen::Matrix< double, 6,6 >::Identity();
// 因为pose为6D的，信息矩阵是6*6的阵，假设位置和角度的估计精度均为0.1且互相独立；那么协方差则为对角为0.01的矩阵，信息阵则为100的矩阵
information(0,0) = information(1,1) = information(2,2) = 100;
information(3,3) = information(4,4) = information(5,5) = 100;
//也可以将角度设大一些，表示对角度的估计更加准确
edge->setInformation( information );
//边的估计即是pnp求解之结果
edge->setMeasurement( T );
//将此边加入图中
globalOptimizer.addEdge(edge);
//调用optimizer.optimize( steps )优化所有边
cout<<“optimizing pose graph, vertices: “<<globalOptimizer.vertices().size()<<endl;
globalOptimizer.save(”./data/result_before.g2o”);
globalOptimizer.initializeOptimization();
globalOptimizer.optimize( 100 ); //可以指定优化步数
1.选择一个线性方程求解器，从 PCG（共轭梯度法）, CSparse（稀疏矩阵）, Choldmod（Cholesky分解对称正定阵）中选（不同的方法主要表现在最终的H矩阵构造不同。），实际则来自 g2o/solvers 文件夹中定义的东东。
2.选择一个 BlockSolver 。
3.选择一个迭代策略，从GN, LM, Doglog中选。
源码解读
#include matches;
DMatch(
int _queryIdx, 此匹配对应的查询图像的特征描述子索引
int _trainIdx, 此匹配对应的训练(模板)图像的特征描述子索引
int _imgIdx, 训练图像的索引(若有多个)
float _distance 两个特征向量之间的欧氏距离，越小表明匹配度越高。);
*/
int main(int argc, char **argv) {
if (argc != 5) {
cout << "usage: pose_estimation_3d2d img1 img2 depth1 depth2" << endl;
return 1;
}
Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);
assert(img_1.data && img_2.data && "Can not load images!");
vector<KeyPoint> keypoints_1, keypoints_2;
vector<DMatch> matches;
// 找到两张彩色图像匹配的特征点并且过滤
find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
cout << "一共找到了" << matches.size() << "组匹配点" << endl;
// 从第一张彩色图像对应的深度图像中读取深度值建立3D(空间)点，深度图为16位无符号数，单通道图像
Mat d1 = imread(argv[3], CV_LOAD_IMAGE_UNCHANGED);
// 彩色图像相机的内参矩阵
Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
// fx 0 cx
// 0 fy cy
// 0 0 1
// 定义变量pts_3d存储3D(空间)点
vector<Point3f> pts_3d;
// 定义变量pts_2d存储2D(图像平面)点
vector<Point2f> pts_2d;
/*
* 遍历每个匹配点，根据匹配点的索引m.queryIdx获取匹配的特征点的坐标，
* 然后根据这个坐标去深度图里面索引对应坐标的深度信息,
* 如果深度信息是零，那么说明这个特征点没有深度值然后跳出此次循环，继续下一次。
* d1是深度图，Mat类型的ptr是指针，获得特征点深度，首先得到行地址，之后列指针(.pt.y)[.pt.x]
*/
for (DMatch m:matches) {
ushort d = d1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
// bad depth
if (d == 0)
continue;
// 5000是尺度 dd理解为像素和实际距离的比例
float dd = d / 5000.0;
// 由像素坐标转为归一化相机平面的坐标即 X/Z Y/Z
Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
// p1[-0.0136303, -0.302687]
//将关键点像素坐标转换为相机归一化坐标记为p1;
//保存第一帧图像的3D点（x, y, z）存入pts_3d;
//此时就完成了3D-2D的配对。
pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));
//保存第二帧对应匹配点的2D点（x, y）存入pts_2d;
pts_2d.push_back(keypoints_2[m.trainIdx].pt);
}
cout << "3d-2d pairs: " << pts_3d.size() << endl;
Mat r, t;
// 通过以上3D-2D的配对点求解r,t,该过程叫做求解PnP,可选择EPNP,DLS等方法.
// Finds an object pose from 3D-2D point correspondences.
solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false);
Mat R;
//r= [-0.02643561464541558;
// 0.03964668696557645;
// 0.05090359687960261]
//t= [-0.1255867099750184;
// -0.007363525258815287;
// 0.06099926588678122]
// solvepnp得到的是旋转向量r,需要通过罗德里格斯公式换为旋转矩阵R.
// Converts a rotation matrix to a rotation vector or vice versa.
cv::Rodrigues(r, R);
// R [0.9979193252225095, -0.05138618904650329, 0.03894200717385431;
// 0.05033852907733768, 0.9983556574295407, 0.0274228694479559;
// -0.04028712992732943, -0.02540552801471818, 0.998865109165653]
cout << "R=" << endl << R << endl;
cout << "t=" << endl << t << endl;
//定义变量pts_3d_eigen存储3D点
VecVector3d pts_3d_eigen;
//定义变量pts_2d_eigen存储2D点
VecVector2d pts_2d_eigen;
for (size_t i = 0; i < pts_3d.size(); ++i) {
pts_3d_eigen.push_back(Eigen::Vector3d(pts_3d[i].x, pts_3d[i].y, pts_3d[i].z));
pts_2d_eigen.push_back(Eigen::Vector2d(pts_2d[i].x, pts_2d[i].y));
}
cout << "calling bundle adjustment by gauss newton" << endl;
// Sophus::SE3d 变换矩阵
Sophus::SE3d pose_gn;
//牛顿高斯法构建误差方程,由相机位姿相机内参获得第一幅图像特征点对应的三维坐标到第二幅图像中的投影（像素坐标），
//与真实提取的第二幅图像中特征点的像素坐标作差即重投影误差, 我们的目的是使用高斯牛顿方法获得符合期望误差的变换矩阵。
bundleAdjustmentGaussNewton(pts_3d_eigen, pts_2d_eigen, K, pose_gn);
// pose by g-n:
// 0.997919325221 -0.0513861890122 0.0389420072614 -0.125586710123
// 0.0503385290405 0.998355657431 0.0274228694545 -0.00736352527141
// -0.0402871300142 -0.0254055280183 0.998865109162 0.0609992659219
// 0 0 0 1
cout << "calling bundle adjustment by g2o" << endl;
// Sophus::SE3d SE3_Rt(R, t); 从R,t构造SE3变换矩阵
// Vector6d se3 = SE3_Rt.log(); SE(3)变换矩阵使用对数映射获得它的李代数se3是一个六维向量
// Vector3d so3 = SO3_R.log(); SO(3)旋转矩阵使用对数映射获得它的李代数so3是一个三维向量
// Sophus::SE3d pose_g2o; 定义的时候会定单位向量作为初始值?
Sophus::SE3d pose_g2o;
//通过以上R,t以及3D点可以计算重投影误差,然后让重投影误差最小,通过g2o方法求解得到更加准确的R,t值也就是变换矩阵Sophus::SE3d pose_g2o。
bundleAdjustmentG2O(pts_3d_eigen, pts_2d_eigen, K, pose_g2o);
return 0;
}
// 寻找特征点的匹配
void find_feature_matches(const Mat &img_1, const Mat &img_2,
std::vector<KeyPoint> &keypoints_1,
std::vector<KeyPoint> &keypoints_2,
std::vector<DMatch> &matches) {
//-- 初始化
Mat descriptors_1, descriptors_2;
// used in OpenCV3
// 使用opencv的 ORB::create() 创建一个特征点检测的 Ptr detector
Ptr<FeatureDetector> detector = ORB::create();
// 使用opencv的 ORB::create() 创建一个特征点描述的 Ptr descriptor
Ptr<DescriptorExtractor> descriptor = ORB::create();
// use this if you are in OpenCV2
// Ptr detector = FeatureDetector::create ( "ORB" );
// Ptr descriptor = DescriptorExtractor::create ( "ORB" );
// 特征点的匹配算法我们采用 DescriptorMatcher::create("BruteForce-Hamming") 暴力匹配算法
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
//-- 第一步:检测 Oriented FAST 角点位置
detector->detect(img_1, keypoints_1);
detector->detect(img_2, keypoints_2);
//-- 第二步:根据角点位置计算 BRIEF 描述子
descriptor->compute(img_1, keypoints_1, descriptors_1);
descriptor->compute(img_2, keypoints_2, descriptors_2);
//-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
vector<DMatch> match;
// BFMatcher matcher ( NORM_HAMMING );
matcher->match(descriptors_1, descriptors_2, match);
//-- 第四步:匹配点对筛选
double min_dist = 10000, max_dist = 0;
//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
for (int i = 0; i < descriptors_1.rows; i++) {
double dist = match[i].distance;
if (dist < min_dist) min_dist = dist;
if (dist > max_dist) max_dist = dist;
}
printf("-- Max dist : %f \n", max_dist);
printf("-- Min dist : %f \n", min_dist);
//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
for (int i = 0; i < descriptors_1.rows; i++) {
if (match[i].distance <= max(2 * min_dist, 30.0)) {
matches.push_back(match[i]);
}
}
}
// 像素坐标转相机归一化坐标
Point2d pixel2cam(const Point2d &p, const Mat &K) {
return Point2d
(
(p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
(p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
);
}
//牛顿高斯法构建误差方程,由相机位姿和相机内参获得第一幅图像特征点对应的三维坐标到第二幅图像中的投影(像素坐标)
//与真实提取的第二幅图像中特征点的像素坐标作差即重投影误差
//想要理解个函数具体做了什么一定好好看看教材的第七章的 Bundel Adjustment 这一小节的内容。
// 实际上上面我么已经用Epnp的方法求出了位姿，但是不准却所以我们要优，优化的方法就是高斯牛顿和g2o
// 下面的方法可以结合第六章的gaussNewton.cpp程序一起学习，高斯牛顿还是那个高斯顿，只不过优化的变量换了，所以误差方程也要重新构建！
/**
*
* @param points_3d
* @param points_2d
* @param K
* @param pose
*
*
points_3d[i] = -0.0374123
-0.830816
2.7448
pose = 1 0 0 0
0 1 0 0
0 0 1 0
pc = -0.0374123
-0.830816
2.7448
*/
void bundleAdjustmentGaussNewton(const VecVector3d &points_3d, const VecVector2d &points_2d, const Mat &K, Sophus::SE3d &pose) {
typedef Eigen::Matrix<double, 6, 1> Vector6d;
const int iterations = 10;
double cost = 0, lastCost = 0;
double fx = K.at<double>(0, 0);
double fy = K.at<double>(1, 1);
double cx = K.at<double>(0, 2);
double cy = K.at<double>(1, 2);
for (int iter = 0; iter < iterations; iter++) {
Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
Vector6d b = Vector6d::Zero();
cost = 0;
//compute cost
for (int i = 0; i < points_3d.size(); i++) {
//根据变化矩阵将世界坐标系下面的3D点转换成相机坐标系下面的3D点
//将3D点重投影到像素平面
Eigen::Vector3d pc = pose * points_3d[i];
double inv_z = 1.0 / pc[2];
// inv_z 0.364325
double inv_z2 = inv_z * inv_z;
// inv_z2 0.132733
// 根据内参数将相机坐标系转换成像素坐标（估计的）
// 第七章的 Bundel Adjustment 像素坐标公式 u = fx*X'/Z' + cx , v = fy*Y'/Z' + cy
Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);
// proj = 318
// 92
// 误差 points_2d 是第二张图片和第一张图片正确匹配的特征点，也就是特征点的位置坐标
// Bundel Adjustment 像素坐标观测值points_2d[i] 减去像素坐标预测值 proj
//计算重投影误差
Eigen::Vector2d e = points_2d[i] - proj;
//计算损失函数 向量的平方范数由squaredNorm()获得，等价于向量对自身做点积，也等同于所有元素的平方和
cost += e.squaredNorm();
Eigen::Matrix<double, 2, 6> J;
//第七章的 Bundel Adjustment 雅克比矩阵 重投影误差关于相机位姿李代数的一阶变化关系
J <<-fx * inv_z, 0, fx * pc[0] * inv_z2, fx * pc[0] * pc[1] * inv_z2,
-fx - fx * pc[0] * pc[0] * inv_z2,
fx * pc[1] * inv_z,
0,
-fy * inv_z,
fy * pc[1] * inv_z2,
fy + fy * pc[1] * pc[1] * inv_z2,
-fy * pc[0] * pc[1] * inv_z2,
-fy * pc[0] * inv_z;
//利用第六讲非线性优化部分 高斯牛顿法用J(T)*J作为牛顿法中二阶Hessian矩阵的近似
//计算增量方程的系数H和g(即代码中的b)
H += J.transpose() * J;
//此时的e就是公式中的f(x)
b += -J.transpose() * e;
}
Vector6d dx;
// 高斯牛顿法 求解detla x dx 每次都会重新定义，每次循环变化的是 pose(变换矩阵) 然后更新H和b 左后算出新的dx，dx就是误差的期望值，符合我们的预期就退出。
//求解增量方程，得到的dx为一个向量，即位姿变化量的李代数
dx = H.ldlt().solve(b);
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
// cost increase, update is not good
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// update your estimation
// 对pose左乘扰动或者说左乘更新量
//更新位姿，Sophus::SE3d::exp(dx)主要将位姿增量的李代数转换到李群。（注意：位姿的更新是左乘位姿变化量）
pose = Sophus::SE3d::exp(dx) * pose;
lastCost = cost;
cout << "iteration " << iter << " cost=" << std::setprecision(12) << cost << endl;
//这是迭代的终止条件 Eigen也提供了norm()范数，返回的是squaredNorm()的根
if (dx.norm() < 1e-6) {
// converge
break;
}
}
cout << "pose by g-n: \n" << pose.matrix() << endl;
}
/**
* vertex and edges used in g2o ba
定义顶点6表示优化变量在流形空间的最小维度；Sophus::SE3d表示变量的维
template
D -> 顶点的最小维度，此处是相机的位姿的李代数表示，故维度为6；
T -> 估计量的类型，此处是SE(3)李代数表示位姿
结合这个程序学习:g2oCurveFitting.cpp
*/
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
// 顶点重置 就是优化标量 就是位姿态
virtual void setToOriginImpl() override {
//内部已经初始化的Sophus::SE3d()的值 单位矩阵 相当于 是 １
_estimate = Sophus::SE3d();
}
// left multiplication on SE3
// 顶点（位姿）的更新 根据增量方程计算出增量之后，就是通过这个函数对估计值进行调整的
virtual void oplusImpl(const double *update) override {
//应该是扰动量，应该就是求出来的detla x
Eigen::Matrix<double, 6, 1> update_eigen;
//顶点的更新，Sophus::SE3d::exp(update_eigen)主要将位姿增量的李代数转换到李群。（注意：位姿的更新是左乘位姿变化量）
// To be more specific, this function computes ``expmat(hat(a))`` with,点进去，源码计算了反对称矩阵
update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
//exp(update_eigen)括号里面实际上是反对称矩阵，只不过源码底层帮咱们实现了
_estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
}
virtual bool read(istream &in) override {}
virtual bool write(ostream &out) const override {}
};
/**
* g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose>
误差模型 模板参数<观测值维度，类型，连接顶点类型>
观测值是像素
顶点是相机位姿
定义边，表示投影误差
结合这个程序学习:g2oCurveFitting.cpp
*/
class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
//Eigen库为了使用SSE加速，所以内存分配上使用了128位的指针，但实际分配的可能时64位或32位。与内存对齐有关系
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
// 定义边的计算输入是什么 输入3D点，根据相机的内参计算像素点
EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}
// 计算误差, 所有误差的和
virtual void computeError() override {
const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
// 定义参与顶点计算的变量 这里就是顶点左乘变换矩阵就会实现位姿变换
Sophus::SE3d T = v->estimate();
//坐标变换求解像素坐标
Eigen::Vector3d pos_pixel = _K * (T * _pos3d);
//归一化
pos_pixel /= pos_pixel[2];
/**
*head<2>()表示提取这个向量的前两维元素，像素坐标u v
_measurement是第二张图片匹配的像素点
所以这个 _error 一定是一个容器 这里是一个vector
调试程序的时候我们可以反推，变量的类型，并不一定真的要程序跑起来
typedef Eigen::Matrix ErrorVector;
*/
_error = _measurement - pos_pixel.head<2>();
}
//这个函数就是用来计算雅克比矩阵的,也就是求每一个待优化变量的偏导数
//计算Jacobian matrix，此处是重投影误差关于相机位姿李代数的导数，书中式（7.46）
virtual void linearizeOplus() override {
const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
//estimate()会返回_estimate
Sophus::SE3d T = v->estimate();
//空间点坐标经过变换矩阵到相机坐标系下
Eigen::Vector3d pos_cam = T * _pos3d;
double fx = _K(0, 0);
double fy = _K(1, 1);
double cx = _K(0, 2);
double cy = _K(1, 2);
double X = pos_cam[0];
double Y = pos_cam[1];
double Z = pos_cam[2];
double Z2 = Z * Z;
// 第二版教材 187页 7.46公式 一阶变化关系2*6雅克比矩阵J的计算公式
_jacobianOplusXi<< -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z, 0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
}
virtual bool read(istream &in) override {}
virtual bool write(ostream &out) const override {}
private:
Eigen::Vector3d _pos3d;
Eigen::Matrix3d _K;
};
/**
*
* @param points_3d
* @param points_2d
* @param K
* @param pose
*/
void bundleAdjustmentG2O(const VecVector3d &points_3d, const VecVector2d &points_2d, const Mat &K, Sophus::SE3d &pose) {
// pose is 6, landmark is 3
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;
// 线性求解器类型
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
// 梯度下降方法，可以从GN, LM, DogLeg 中选
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
// 图模型
g2o::SparseOptimizer optimizer;
// 设置求解器,用的是高斯牛顿
optimizer.setAlgorithm(solver);
// 打开调试输出 就是那些红色的输出 使用cerr输出的所以是红色的
optimizer.setVerbose(true);
// 建立顶点 camera vertex_pose
VertexPose *vertex_pose = new VertexPose();
//Vertex独一无二的ID值,edge通过这个ID来与其建立联系
vertex_pose->setId(0);
//第一个参数指定上一步添加Vertex时的索引,这样edge就可以通过这个索引值和Vertex联系起来了,初始化参与顶点计算的值
vertex_pose->setEstimate(Sophus::SE3d());
// 添加顶点
optimizer.addVertex(vertex_pose);
// K
Eigen::Matrix3d K_eigen;
K_eigen <<K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);
/**
* edge
*/
int index = 1;
for (size_t i = 0; i < points_2d.size(); ++i) {
auto p2d = points_2d[i];
auto p3d = points_3d[i];
EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
// 设置边连接的顶点，序号从0开始，一元边连接一个顶点，故只设置序号为0的顶点
edge->setId(index);
/**
*第一个参数指定上一步添加Vertex时的索引,这样edge就可以通过这个索引值和Vertex联系起来了
设置连接的顶点
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV
//李群相机位姿v1
const VertexSE3Expmap* v1 = static_cast(_vertices[1]);
顶点v2
const VertexSBAPointXYZ* v2 = static_cast(_vertices[0]);
_vertices[0] 对应的是VertexSBAPointXYZ 类型的顶点，也就是三维点，
_vertices[1] 对应的是VertexSE3Expmap 类型的顶点，也就是位姿pose。
因此前面 1 对应的就应该是 pose，0对应的 应该就是三维点。
*/
edge->setVertex(0, vertex_pose);
//measurement：存储观测数值 特征点的图像坐标(x,y)
edge->setMeasurement(p2d);
/**
* 信息矩阵：协方差矩阵之逆
*
* |方差构成了对角线上的元素|方差度量单个随机变量的离散程度
* 协方差矩阵|
* |协方差构成了非对角线上的元素|协方差刻画两个随机变量的相似程度
*
* Eigen::Matrix2d::Identity()
* 1 0
* 0 1
*
* Eigen::Matrix::Identity()
* 1
*
* 协方差矩阵主要是为了设置权重的，控制噪声的
*/
edge->setInformation(Eigen::Matrix2d::Identity());
//添加边
optimizer.addEdge(edge);
index++;
}
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
//optimizer终极大bose 执行优化前的初始化
optimizer.setVerbose(true);
optimizer.initializeOptimization();
//开始执行优化,并设置迭代次数
optimizer.optimize(10);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;
// 最终估计的位姿
pose = vertex_pose->estimate();
}