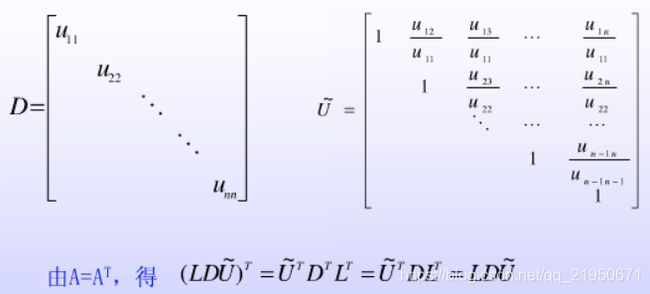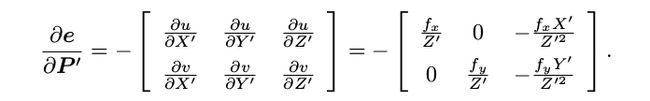【视觉SLAM十四讲源码解读】曲线拟合项目实战教程G2O图优化 雅可比矩阵推导

高斯牛顿曲线拟合 1_gauss_newton_curve_fitting.cpp

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;
using namespace Eigen;

int main(int argc, char **argv) {
  // 真实参数值
  double a_real = 1.0, b_real = 2.0, c_real = 1.0;
  // 估计参数值 estimated abc = 0.890912, 2.1719, 0.943629
  double a_estimated = 2.0, b_estimated = -1.0, c_estimated = 5.0;
  double inv_sigma = 1.0 / 1.0;// 噪声Sigma值的倒数
  cv::RNG rng;                     // OpenCV随机数产生器

  // 根据真实的参数值a_real = 1.0, b_real = 2.0, c_real = 1.0 生成真实的x_data,y_data
  // 定义存储真实x_data,y_data的vector
  vector<double> x_real_data, y_real_data;
  for (int i = 0; i < 100; i++){
    // 假设x的真实值
    double x_real = i / 100.0;
    x_real_data.push_back(x_real);
    y_real_data.push_back(exp(a_real * x_real * x_real + b_real * x_real + c_real) + rng.gaussian(1.0 * 1.0));
  }

  cout
  <<"Un-estimated a_estimated = " << a_estimated
  << ", b_estimated = " << b_estimated
  << ", c_estimated = " << c_estimated << endl;

  // 开始Gauss-Newton迭代
  int iterations = 100;           // 迭代次数
  double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost

  // 一共进行一百次迭代，每一次迭代会计算总的误差
  for (int iter = 0; iter < iterations; iter++) {

    // Hessian = J^TJ in Gauss-Newton 高斯牛顿法用J^TJ作为牛顿法中二阶Hessian矩阵的近似
    Matrix3d H = Matrix3d::Zero();
    Vector3d b = Vector3d::Zero(); // bias
    cost = 0;

    // 构造最小二乘问题,总的误差的平方最小
    for (int i = 0; i < 100; i++) {
      double xi = x_real_data[i], yi = y_real_data[i];// 第i个数据点
      // 真实y值和估计y值做差 真实的yi值和估计的参数值算出来的值做差
      double error = yi - exp(a_estimated * xi * xi + b_estimated * xi + c_estimated);
      Vector3d J; // 定义雅可比矩阵
      J[0] = -xi * xi * exp(a_estimated * xi * xi + b_estimated * xi + c_estimated);  // de/da
      J[1] = -xi * exp(a_estimated * xi * xi + b_estimated * xi + c_estimated);       // de/db
      J[2] = -exp(a_estimated * xi * xi + b_estimated * xi + c_estimated);            // de/dc

      // 高斯牛顿法用J^TJ 作为牛顿法中二阶 Hessian　矩阵的近似
      H += inv_sigma * inv_sigma * J * J.transpose();
      b += -inv_sigma * inv_sigma * error * J;

      // 最小二乘　总的误差平方和
      cost += error * error;
    }

    // 求解线性方程 Hdx=b
    // Matrix3d H = Matrix3d::Zero(); // Hessian = J^TJ in Gauss-Newton
    // Vector3d b = Vector3d::Zero(); // bias
    // 高斯牛顿法用J^TJ 作为牛顿法中二阶 Hessian　矩阵的近似
    // H += inv_sigma * inv_sigma * J * J.transpose();
    // b += -inv_sigma * inv_sigma * error * J;
    Vector3d dx = H.ldlt().solve(b);
    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }

    // 迭代结束条件本次迭代的cost等于或者大于上一次迭代的cost
    if (iter > 0 && cost >= lastCost) {
      cout
      << "\ncost: "<< cost
      << " last cost: " << lastCost
      << " cost >= last cost: "  << endl;
      break;
    }

    a_estimated += dx[0];
    b_estimated += dx[1];
    c_estimated += dx[2];

    // 用lastCost保存本次迭代所有数据总的误差
    lastCost = cost;

    cout
    << setprecision(9) << "cost: " << cost
    << ",\tupdate: "<< dx.transpose()
    << ",\testimated params: " << a_estimated << "," << b_estimated << "," << c_estimated << endl;

  }

  cout
  << "have-estimated a_estimated = " << a_estimated
  << ", b_estimated = " << b_estimated
  << ", c_estimated = " << c_estimated << endl;
  return 0;
}

CMakeLists.txt

cmake_minimum_required( VERSION 2.8 )

project( curve_fitting )

set(CMAKE_BUILD_TYPE Debug)
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )

find_package( OpenCV REQUIRED )

add_executable(1_gauss_newton_curve_fitting 1_gauss_newton_curve_fitting.cpp)
target_link_libraries(1_gauss_newton_curve_fitting ${OpenCV_LIBS})

运行结果

矩阵分解是将矩阵拆解为数个矩阵的乘积，可分为三角分解、满秩分解、QR分解、Jordan分解和SVD（奇异值）分解、非负矩阵分解等，常见的有三种：1)三角分解(Triangular Factorization)，2)QR 分解法 (QR Factorization)，3)奇异值分解 (Singular Value Decomposition)。

1. LU分解

三角分解(LU分解)：是矩阵分解的一种，可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积（有时是它们和一个置换矩阵的乘积）。LU分解主要应用在数值分析中，用来解线性方程、求反矩阵或计算行列式。

2. LDLT分解法

实际问题中，当求解方程组的系数矩阵是对称矩阵时，则用下面介绍的LDLT分解法可以简化程序设计并减少计算量。

从定理可知，当矩阵A的各阶顺序主子式不为零时，A有唯一的Doolittle分解A= LU。矩阵U的对角线元素Uii 不等于0，将矩阵U的每行依次提出，

定理：若对称矩阵A的各阶顺序主子式不为零时，则A可以唯一分解为A= LDLT，这里

LT为L的转置矩阵。

当A有LDLT分解时，利用矩阵运算法则及相等原理易得计算ljk和dk的公式为

3. Cholesky分解

Cholesky分解是一种分解矩阵的方法, 在线形代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积（那实数界来类比的话，此分解就好像求平方根）。与一般的矩阵分解求解方程的方法比较，Cholesky分解效率很高。

Cholesky分解的条件

一、Hermitianmatrix：矩阵中的元素共轭对称（复数域的定义，类比于实数对称矩阵）。Hermitiank意味着对于任意向量x和y，(x*)Ay共轭相等

二、Positive-definite：正定（矩阵域，类比于正实数的一种定义）。正定矩阵A意味着，对于任何向量x，(x^T)Ax总是大于零(复数域是(x*)Ax>0)

Cholesky分解的形式

可记作A = L L*。其中L是下三角矩阵。L*是L的共轭转置矩阵。

可以证明，只要A满足以上两个条件，L是唯一确定的，而且L的对角元素肯定是正数。反过来也对，即存在L把A分解的话，A满足以上两个条件。

Hermitianmatrix：矩阵中的元素共轭对称（复数域的定义，类比于实数对称矩阵）。Hermitiank意味着对于任意向量x和y，(x*)Ay共轭相等

Positive-definite：正定（矩阵域，类比于正实数的一种定义）。正定矩阵A意味着，对于任何向量x，(x^T)Ax总是大于零(复数域是(x*)Ax>0)
如果A是半正定的（semi-definite），也可以分解，不过这时候L就不唯一了。

特别的，如果A是实数对称矩阵，那么L的元素肯定也是实数。

另外，满足以上两个条件意味着A矩阵的特征值都为正实数，因为Ax = lamda * x,

(x*)Ax = lamda * (x*)x > 0, lamda > 0

4. QR分解

矩阵的QR分解是指，可以将矩阵A分级成一个正交阵Q和一个上三角矩阵R的乘积。实际中，QR分解经常被用来解线性最小二乘问题

对于非方阵的m∗n(m≥n)m∗n(m≥n)阶矩阵A也可能存在QR分解。这时Q为mm阶的正交矩阵，R为mn阶上三角矩阵。这时的QR分解不是完整的(方阵)，因此称为约化QR分解(对于列满秩矩阵A必存在约化QR分解)。同时也可以通过扩充矩阵A为方阵或者对矩阵R补零，可以得到完全QR分解。

5. SVD分解

对任意矩阵，都能被奇异值分解为

其中是的正交矩阵，是的正交矩阵，是由个沿对角线从大到小排列的奇异值

组成的方阵，就是矩阵的秩。奇异值分解是一种正交矩阵分解法。

SVD分解常用在信息压缩，以及求广义逆：

5.1 SVD与广义逆矩阵

   在认识矩阵的广义逆之前，先来回顾一下方阵的逆。

   对于一个的方阵，如果存在一个矩阵，使得，那么方阵的逆为。

   那么对于非方阵来说情况又是怎样的？ 比如对于的矩阵，它的逆是怎样计算的？这就是我将要    讨论的广义逆矩阵。   矩阵的广义逆由Moore在1920年提出，后来在1955年经过Penrose发展得到如下定义    对任意复数矩阵，如果存在的矩阵，满足

则称为的一个Moore-Penrose逆，简称广义逆，记为。并把上面四个方程叫做Moore-Penrose 方程，简称M-P方程。

由于M-P的四个方程都各有一定的解释，并且应用起来各有方便之处，所以出于不同的目的，常常考虑满足

部分方程的，叫做弱逆，弱逆不唯一。为了引用方便，下面给出广义逆矩阵的定义
对于的矩阵，若存在的矩阵，满足M-P方程中的全部或者其中的一部分，则称为的广义逆矩阵。

实际上有结论：如果满足M-P方程中的全部四个条件，那么得到的矩阵是唯一的，如果只满足部分条件，

那么得到的矩阵不唯一。也就是说一个矩阵的Moore-Penrose逆是唯一的。

而广义逆的计算可以利用的SVD分解得到，假设矩阵的SVD分解为那么，不难验证

有了广义逆矩阵，那么就可以用来求解线性方程组，假设现在已经知道了矩阵的广义逆，

如果矩阵的秩是，则其唯一解是，如果秩小于，则有无穷多组解，其中最小范数解仍然是，通常我们关心的也就是这个解。

ceres曲线拟合 2_ceres_curve_fitting.cpp

#include 
#include 
#include 
#include 

using namespace std;

// 代价函数的计算模型
struct CURVE_FITTING_COST{
    CURVE_FITTING_COST (double x, double y):_x(x),_y(y){}
    // 残差的计算
    template <typename T>
    bool operator() (
            // 模型参数3维
            const T* const abc,
            // 残差
            T* residual) const
    {
        // y-exp(ax^2+bx+c)
        residual[0] = T (_y) - ceres::exp(abc[0]*T(_x) *T( _x) + abc[1]*T(_x) + abc[2]);
        return true;
    }
    // x,y数据
    const double _x, _y;
};

int main() {
    cv::RNG rng;// OpenCV随机数生成器
    double a_real = 1.0, b_real = 2.0, c_real = 1.0;// 真实参数值
    // 根据真实参数值a_real = 1.0, b_real = 2.0, c_real = 1.0 生成真实的x_data,y_data
    vector<double> x_real_data, y_real_data;
    for (int i = 0; i < 100; i++) {
        // 假设x的真实值
        double x_real = i / 100.0;
        x_real_data.push_back(x_real);
        y_real_data.push_back(exp(a_real * x_real * x_real + b_real * x_real + c_real) + rng.gaussian(1.0 * 1.0));
    }
    // 估计参数值
    double a_estimated = 2.0, b_estimated = -1.0, c_estimated = 5.0;
    double abc[3] = {a_estimated, b_estimated, c_estimated};
    // 构建最小二乘问题
    ceres::Problem problem;
    // 问题中添加误差项
    for (int i = 0; i < 100; i++) {
        problem.AddResidualBlock(
                // 自动求导模板参数 <误差类型,输出维度,输入维度> 维数要与前面struct中一致
                new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
                        new CURVE_FITTING_COST(x_real_data[i], y_real_data[i])),
                nullptr,                                             // 核函数不使用为空
                abc);                                                        // 待估计参数
    }
    // 配置求解器
    ceres::Solver::Options options;
    // 增量方程如何求解
    options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;
    // options.linear_solver_type = ceres::DENSE_QR;
    // 输出到cout
    options.minimizer_progress_to_stdout = true;
    // 优化信息
    ceres::Solver::Summary summary;
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    // 开始优化
    ceres::Solve(options, &problem, &summary);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
    // 输出结果
    cout << summary.BriefReport() << endl;
    cout << "estimated a,b,c = ";
    for (auto a:abc) cout << a << " ";
    cout << endl;
    return 0;
}

CMakeLists.txt

cmake_minimum_required( VERSION 2.8 )

project(curve_fitting)

set(CMAKE_BUILD_TYPE Debug)
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )

find_package(OpenCV REQUIRED)

set(CERES_LIBRARIES /usr/local/lib/libceres.a)
include_directories(/usr/local/include/ceres)

add_executable( 2_ceres_curve_fitting 2_ceres_curve_fitting.cpp)
target_link_libraries( 2_ceres_curve_fitting ${OpenCV_LIBS} ${CERES_LIBRARIES} cxsparse glog cholmod lapack blas pthread)

g2o曲线拟合

曲线拟合误差方程和雅克比矩阵详细计算推导

上面是公式，下面是代码，接下来是详细的计算过程

  virtual void linearizeOplus() override {
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    const Eigen::Vector3d abc = v->estimate();
    double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
    _jacobianOplusXi[0] = -_x * _x * y;
    _jacobianOplusXi[1] = -_x * y;
    _jacobianOplusXi[2] = -y;
  }

常数求导数

指数函数求导

复合函数求导数

偏导
偏导数就是函数关于某个变量的变化率，偏导数可以用来求多元函数的极值，深刻一点的，偏导数用来表示函数的Taylor展开，函数的梯度，方向导数，再然后，在微分几何里，∂/∂xi可以作为切空间的基，可以用来求丛上的联络还有很多其他的方面

3_g2o_curve_fitting.cpp源码解读

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;


/**
 * 定义 曲线拟合 顶点(待优化变量)模板参数<优化变量的维度, 优化变量的数据类型>
 * Templatized BaseVertex
 * D: minimal dimension of the vertex, 3 for rotation in 3D
 * T: internal type to represent the estimate, Quaternion for rotation in 3D
 */
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    // 待优化变量的初始值
    virtual void setToOriginImpl(){
        _estimate << 0, 0, 0;
    }
    // 待优化变量如何更新
    virtual void oplusImpl( const double* update ){
        _estimate += Eigen::Vector3d(update);
    }
    // 读
    virtual bool read( istream& in ) {}
    // 写
    virtual bool write( ostream& out ) const {}
};


/**
 * 定义 曲线拟合模型 边(误差)模板参数
 * template 
 * linearizeOplus() 计算雅可比矩阵(优化变量的导数)
 */
class CurveFittingEdge: public g2o::BaseUnaryEdge<1, double, CurveFittingVertex>{

public:
    double _x;  // x 的值， y 的值为 _measurement

public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    // 构造函数
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    // 曲线拟合模型 如何计算误差
    void computeError() {
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
    }
    // 曲线拟合模型 计算雅可比矩阵
    virtual void linearizeOplus() override {
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        const Eigen::Vector3d abc_estimated = v->estimate();
        double y = exp(abc_estimated[0] * _x * _x + abc_estimated[1] * _x + abc_estimated[2]);
        _jacobianOplusXi[0] = -_x * _x * y;
        _jacobianOplusXi[1] = -_x * y;
        _jacobianOplusXi[2] = -y;
    }

    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}

};

// 整体思路就是构造了一个函数，然后用这个函数生成y值，然后用G2O去反推生成y值的参数a b c 分别是啥！
int main(){
    // 参数abc的真值
    double a_real = 1.0, b_real = 2.0, c_real = 1.0;
    // OpenCV随机数产生器
    cv::RNG rng;
    // 根据真实的参数值a_real = 1.0, b_real = 2.0, c_real = 1.0 生成真实的x_data,y_data
    vector<double> x_real_data, y_real_data;
    for (int i=0; i<100; i++){
        double x = i/100.0;
        x_real_data.push_back ( x );
        // 噪声正态分布期望均数μ,标准差σ,方差σ^2
        y_real_data.push_back (exp ( a_real*x*x + b_real*x + c_real ) + rng.gaussian ( 1.0 ));
    }

    // 用viz可视化真实数据
    cv::Mat point_cloud = cv::Mat::zeros(x_real_data.size(), y_real_data.size(), CV_32FC3);// 生成点云
    for (size_t i = 0; i < x_real_data.size(); i++) {
        point_cloud.at<cv::Vec3f>(i)[0] = x_real_data[i];
        point_cloud.at<cv::Vec3f>(i)[1] = y_real_data[i];
        point_cloud.at<cv::Vec3f>(i)[2] = 0;
    }
    cv::viz::Viz3d window("window");// 窗口
    cv::viz::WCloud cloud(point_cloud, cv::viz::Color::yellow());//创建点云
    window.showWidget("cloud", cloud);//将点云放在窗口上
    while (!window.wasStopped()) {
        window.spinOnce(1, true);
    }

    // 创建稀疏优化器, 选择优化方法: GN, LM, DogLeg
    g2o::SparseOptimizer optimizer;
    typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;  // 待优化变量维度为3，误差变量维度为1
    typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器
    auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
    // 设置求解器
    optimizer.setAlgorithm( solver );
    // 打开调试输出(终端红色的输出)
    optimizer.setVerbose( true );
    // 创建顶点(待优化变量)
    CurveFittingVertex* v = new CurveFittingVertex();
    // 待优化变量的初始值　a_estimated = 0.0, b_estimated = 0.0, c_estimated = 0.0
    // 最终优化得到的是 estimated model: 0.890912   2.1719 0.943629
    v->setEstimate( Eigen::Vector3d(0,0,0) );
    // 待优化变量的ID编号(从零开始,只有１个顶点)
    v->setId(0);
    // 向优化器添加待优化变量
    optimizer.addVertex( v );
    // 向优化器添加边(误差项)
    for ( int i=0; i<100; i++ ){
        // x值
        CurveFittingEdge* edge = new CurveFittingEdge( x_real_data[i] );
        // y值
        edge->setMeasurement( y_real_data[i] );
        // 定义边编号(从零开始,有100个边)
        edge->setId(i);
        // 初始化该边(设置边所连接的顶点)
        edge->setVertex( 0, v );
        /**
         * 信息矩阵：协方差矩阵之逆
         *          |方差构成了对角线上的元素|方差度量单个随机变量的离散程度
         * 协方差矩阵|
         *         |协方差构成了非对角线上的元素|协方差刻画两个随机变量的相似程度
         *
         *         Eigen::Matrix2d::Identity()
         *                        1 0
         *                        0 1
         *         Eigen::Matrix::Identity()
         *                      　1
         *         协方差矩阵主要是为了设置权重控制噪声
         */
        edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(1.0*1.0) );
        optimizer.addEdge( edge );
    }

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    // 初始化图
    optimizer.initializeOptimization();

    // 设置优化次数
    optimizer.optimize(100);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );
    cout<<"solve time cost = "<<time_used.count()<<" seconds. "<<endl;

    // 输出优化值的值
    Eigen::Vector3d abc_estimate = v->estimate();
    cout<<"estimated model: "<<abc_estimate.transpose()<<endl;
    return 0;
}

CMakeLists.txt编译文件

cmake_minimum_required(VERSION 2.8)

project(ch6)

set(CMAKE_BUILD_TYPE Debug)
set(CMAKE_CXX_FLAGS "-std=c++14 -O3")

# OpenCV
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})

# Eigen
include_directories("/usr/include/eigen3")


#cmake .. -D CMAKE_INSTALL_PREFIX=/home/q/slambook2/3rdparty/g2o/install
include_directories(/home/q/slambook2/3rdparty/g2o/install/include)
link_directories(/home/q/slambook2/3rdparty/g2o/install/lib)

# 添加Pangolin依赖
find_package( Pangolin )
include_directories( ${Pangolin_INCLUDE_DIRS} )

add_executable(g2oCurveFitting g2oCurveFitting.cpp)
target_link_libraries(g2oCurveFitting ${OpenCV_LIBS} ${Pangolin_LIBRARIES} g2o_core g2o_stuff)

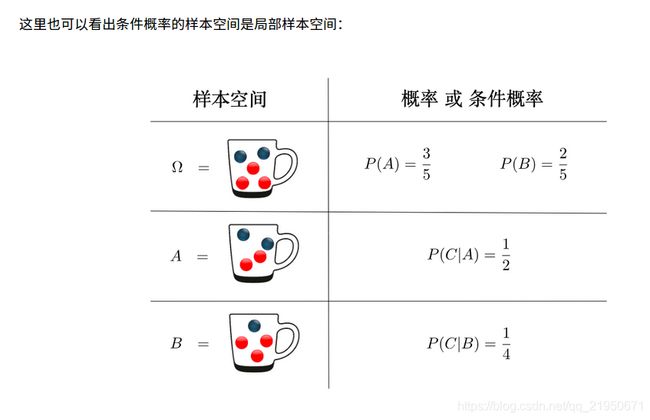
条件概率

条件概率是指事件A在事件B发生的条件下发生的概率。
条件概率表示为：P（A|B），读作“A在B发生的条件下发生的概率”。
条件概率公式：设A，B是两个事件，且P(B)>0，则在事件B发生的条件下，事件A发生的条件概率，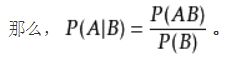

条件概率公式：设A，B是两个事件，且P(B)>0，则在事件B发生的条件下，事件A发生的条件概率， P(A|B)=P(AB)/P(B)

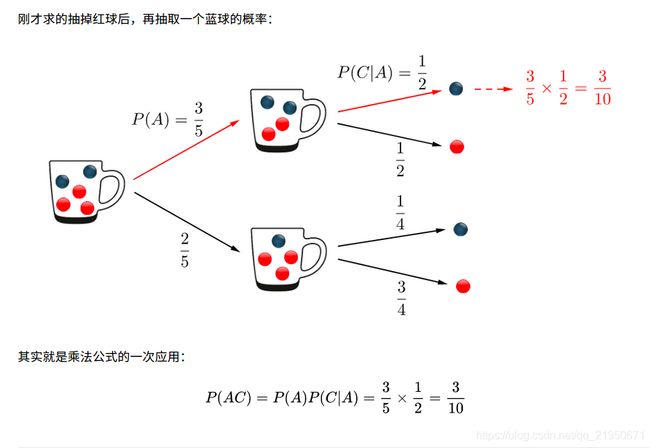
乘法公式

贝叶斯与全概率

贝叶斯定理

贝叶斯模型

贝叶斯模型的建立主要有3个概念：1.先验概率。2.最大似然函数。3.后验概率
所谓贝叶斯公式，是指当分析样本大到接近总体数时，样本中事件发生的概率将接近于总体中事件发生的概率。用来描述两个条件概率之间的关系。

贝叶斯公式，其实就是条件概率、乘法公式、全概率公式的组合。以上四个公式的研究对象，都是“同一实验下的不同的结果集合”
为了容易理解这四个概率公式，可以把用“样本数目公式”来代替“概率公式”，来求概率。

先验概率是指根据以往经验和分析得到的概率，如全概率公式 中的 ，它往往作为“由因求果”问题中的“因”出现。

后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的“因” 。后验概率是基于新的信息，修正原来的先验概率后所获得的更接近实际情况的概率估计。

先验概率和后验概率是相对的。如果以后还有新的信息引入，更新了现在所谓的后验概率，得到了新的概率值，那么这个新的概率值被称为后验概率。

最大似然估计

最大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。
简单而言，假设我们要统计全国人口的身高，首先假设这个身高服从服从正态分布，但是该分布的均值与方差未知。
我们没有人力与物力去统计全国每个人的身高，但是可以通过采样，获取部分人的身高，然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。

最大后验概率

最大后验概率（MAP）：
最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似，但是最大的不同时，最大后验估计的融入了要估计量的先验分布在其中。故最大后验估计可以看做规则化的最大似然估计。

以高斯分布的均值和方差仅仅针对x变量，y值代表x出现的概率，所以期望值是x与y相乘得到；根据函数的对称性就知道期望是0，方差通过计算为1；

概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。

最小二乘

最小二乘->最小平方和问题->也就是最小误差下等价于状态的最大似然，这里面的最大似然理论就是用于求最小化误差下的参数也就是观测方程和运动方程的对应参数最小化。

高斯分布

高斯分布（Gaussian distribution）又称正态分布（Normal distribution），
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
当μ = 0,σ = 1时的正态分布是标准正态分布。

标准差和均值的量纲（单位）是一致的，在描述一个波动范围时标准差比方差更方便。比如一个班男生的平均身高是170cm,标准差是10cm,那么方差就是10cm^2。可以进行的比较简便的描述是本班男生身高分布是170±10cm，方差就无法做到这点。
再举个例子，从正态分布中抽出的一个样本落在[μ-3σ, μ+3σ]这个范围内的概率是99.7%，也可以称为“正负3个标准差”。如果没有标准差这个概念，我们使用方差来描述这个范围就略微绕了一点。万一这个分布是有实际背景的，这个范围描述还要加上一个单位，这时候为了方便，人们就自然而然地将这个量单独提取出来了。

期望可以理解为平均值。

理解概率密度函数
理解为随机变量和对应概率之间的映射集合 因为函数就是一种特殊的映射。

最大似然估计-高斯分布

图优化原理算法解析

视觉slam中的主流优化方法是图优化(graph-based optimization)

图优化本质优化问题有三个最重要因素：目标函数、优化变量、优化约束。

很多时候目标函数$F(x)$的形式复杂，没法写出导数的解析形式，难以求解导数为零的方程。
因此使用迭代方式求解，从一个初值$x_0$出发，不断地推导当前值附近的能使目标函数下降的方向（反向梯度），然后沿着梯度方向走出一步，使得函数值下降一点，反复迭代，理论上对于任何函数，都能找到一个极小值点。

迭代的策略主要体现在如何选择下降方向和步长两方面。
主要有 Gauss-Newton(GN)法和 Levenberg-Marquardt(LM)法两种，主要在迭代策略上有所不同，但是寻找梯度并迭代是一样的。

图优化，就是把一个常规的优化问题，以图(Graph)的形式表述，以顶点表示优化变量，以边表示观测方程。

优化变量举例

• 机器人的Pose6自由度下为4×4的变换矩阵$T$或者3自由度下的位置与转角$[x,y,\theta ]$
• 三维空间点$[x,y,z]$
• 二维空间点$[x,y]$

观测方程举例

---

机器人两个Pose之间的变换；
Binary Edge(二元边)，顶点为两个Pose，边的方程方程为$T_1$ = $\Delta$$T\ast T_2$

---

机器人的某个Pose处用激光观测到了某个空间点，得到了它距离自己的距离与角度；
Binary Edge(二元边)，顶点为一个2D Pose:$[x,y,\theta {]}^T$和一个Point:$[{\lambda }_x,{\lambda }_y{]}^T$,
观测数据是距离$r$和角度$b$
观测方程为:

$\left[\begin{array}{c}r\\ b\end{array}\right]$ = $\left[\begin{array}{c}\sqrt{({\lambda }_x-x{)}^2+({\lambda }_y-y{)}^2}\\ {\tan }^{-1}(\frac{{\lambda }_y-y}{{\lambda }_x-x})-\theta \end{array}\right]$

---

机器人在某个Pose处用相机观测到了某个空间点，得到了它的像素坐标；
Binary Edge(二元边)，顶点为一个3D Pose $T$ 和一个空间点 $X=[x,y,z{]}^T$
观测数据为像素坐标$z=[u,v{]}^T$
观测方程为：$z=K(R\ast X+t)$
$K$为相机内参，$R$为旋转矩阵,$t$为平移向量

---

假设一个带有$n$条边的图，其目标函数可以写成：

$$\underset{x}{\min }\sum _{k=1}^n{e}_k(x_k,z_k{)}^T{\Omega }_k{e}_k(x_k,z_k)$$

$e$函数在原理上表示一个误差，是一个矢量，作为优化变量$x_k,z_k$符合程度的一个度量。
它越大表示$x_k$越不符合$z_k$。
由于目标函数必须是标量，所以必须用它的平方形式来表达目标函数。
最简单的形式是直接做成平方：$$e(x,z{)}^{T}e(x,z)$$
进一步，为了表示我们对误差各分量重视程度的不一样，还使用一个信息矩阵$\Omega$来表示各分量的不一致性。

信息矩阵$\Omega$是协方差矩阵的逆，是一个对称矩阵。它的每个元素${\Omega }_{i,j}$作为$e_i$$e_j$的系数，可以看成我们对$e_i$$e_j$这个误差项相关性的一个预计。
最简单的是把$\Omega$设成对角矩阵，对角阵元素的大小表明我们对此项误差的重视程度。

这里的$x_k$可以指一个顶点、两个顶点或多个顶点，取决于边的实际类型。
所以，更严谨的方式是把它写成$e_k(z_k,x_{k1},x_{k2})$，但是那样写法实在是太繁琐，
由于$z_k$是已知的，为了数学上的简洁，我们再把它写成$e_k(x_k)$的形式。
于是总体优化问题变为n条边加和的形式：
$$\underset{x}{\min }\sum _{k=1}^n{e}_k(x_k{)}^T{\Omega }_k{e}_k(x_k)$$

重复一遍，边的具体形式有很多种，可以是一元边、二元边或多元边，它们的数学表达形式取决于传感器或你想要描述的东西。例如视觉SLAM中，在一个相机Pose $T_k$ 处对空间点$X_k$进行了一次观测，得到$z_k$，那么这条二元边的数学形式即为

$e_k(x_k,T_k,z_k)=(z_k-K(R{x}_k+t){)}^T{\Omega }_k(z_k-K(R{x}_k+t))$

单个边其实并不复杂。现在，我们有了一个很多个节点和边的图，构成了一个庞大的优化问题。我们并不想展开它的数学形式，只关心它的优化解。那么，为了求解优化，需要知道两样东西：一个初始点和一个迭代方向。为了数学上的方便，先考虑第$k$条边$e_k(x_k)$吧。

我们假设它的初始点为$\widetilde{x_k}$,并且给它一个$\Delta x$的增量，那么边的估计值就变为$F_k(\widetilde{x_k}+\Delta x)$,而误差则从$e_k(\tilde{x})$变为$e_k(\widetilde{x_k}+\Delta x)$。首先对误差项进行一阶展开：

$e_k(\widetilde{x_k}+\Delta x)$$\approx$$e_k(\widetilde{x_k})$＋$\frac{d{e}_k}{d{x}_k}\Delta x$ = $e_k+J_k\Delta x$

这里的$J_k$是e_k关于$x_k$,矩阵形式下为雅克比矩阵。我们在估计点附近做了一次线性假设，认为函数值是能够用一阶导数来逼近的，当然这在 $\Delta x$很大的时候就不成立了。
于是，对于第$k$条边的目标函数项，有：
进一步展开：

$F_k(\tilde{x}+\Delta x)=e_k(\widetilde{x_k}+\Delta x{)}^T{\Omega }_k{e}_k(\widetilde{x_k}+\Delta x)$
$\approx$$(e_k+J_k\Delta x{)}^T{\Omega }_k(e_k+J_k\Delta x)$
$=e{}_k^T{\Omega }_k{e}_k+2e{}_k^T{\Omega }_k{J}_k\Delta x+\Delta x^T{J}_k^T{\Omega }_k{J}_k\Delta x$
$=C_k+2b_k\Delta x+\Delta x^T{H}_k\Delta x$

最后一个式子是定义整理式，我们把和$\Delta x$无关的整理成常数项$C_k$,把一次项系数写成$2b_k$，$H_k$,注意二次项系数其实就是Hessian矩阵。

这里$C_k$实际上就是该边变化前的取值，所以$x_k$发生增量后，目标函数$F_k$项改变的值即为
$\Delta F_k$　＝　$2b_k\Delta x+\Delta x^T{H}_k\Delta x$

我们的目标是找到$\Delta x$，使得这个增量变为极小值，所以直接令它对于$\Delta x$的导数为零，有:

$\frac{d{F}_k}{d\Delta x}$ = $2b+2H_k\Delta x$ = $0$ $⟹$ $H_k\Delta x$ = $-b_k$

所以归根结底，我们在求解一个线性方程组：
$H_k\Delta x$ = $-b_k$

所以把所有边放到一起考虑进去，就可以去掉下标，直接说我们要求解
$H\Delta x$ = $-b$

SLAM构建的图，并非是全连通图，它往往是很稀疏的。
例如一个地图里大部分路标点，只会在很少的时刻被机器人看见，从而建立起一些边。
体现在数学公式中，虽然总体目标函数()有很多项，但某个顶点就只会出现在和它有关的边里面！
这导致许多和$x_k$无关的边，比如说$e_j$，对应的雅可比$J_j$就直接是个零矩阵！
而总体的雅可比$J$中，和$x_k$有关的那一列大部分为零，只有少数的地方，也就是和$x_k$顶点相连的边，出现了非零值。

相应的二阶导矩阵$H$中，大部分也是零元素。这种稀疏性能很好地帮助我们快速求解上面的线性方程。稀疏代数库包括SBA、PCG、CSparse、Cholmod等等。g2o正是使用它们来求解图优化问题的。在数值计算中，我们可以给出雅可比和海塞的解析形式进行计算，也可以让计算机去数值计算这两个阵，而我们只需要给出误差的定义方式即可。

图优化流程

选择你想要的图里的节点与边的类型，确定它们的参数化形式；
往图里加入实际的节点和边；
选择初值，开始迭代；
每一步迭代中，计算对应于当前估计值的雅可比矩阵和海塞矩阵；
求解稀疏线性方程Δ=−，得到梯度方向；
继续用GN或LM进行迭代。如果迭代结束，返回优化值。
实际上，g2o能帮你做好第3-6步，你要做的只是前两步而已。

深入理解图优化与g2o：图优化篇

图优化后端代码实践

代码将手写图优化后端作为重点，仅依赖 Eigen, 实现后端系统在精度上和ceres 以及g2o不相上下。

在g2o中选择优化方法一共需要三个步骤：

• 选择一个线性方程求解器，从 PCG, CSparse, Choldmod中选，实际则来自 g2o/solvers 文件夹中定义的东东。
• 选择一个 BlockSolver 。
• 选择一个迭代策略，从GN, LM, Doglog中选。

双视图bundle adjustment
代码的git地址：https://github.com/gaoxiang12/g2o_ba_example

两种思路。其一是通过特征点来求，其二是直接通过像素来求。第一种也叫做 sparse 方式，第二种叫做相对的 dense 方式。由于主流仍在用特征点，所以我们例程也用特征点。

特征点方法的观点是：一个图像可以用几百个具有代表性的，比较稳定的点来表示。一旦我们有了这些点，就可以忽略图中的其余部分，而只关注这些点。（dense 思路则反对这一观点，认为它丢弃了图像大部分信息，毕竟一个640x480的图有30万个点，而特征点只有几百个）。

G20基础知识讲解

SLAM的后端一般分为两种处理方法：

一种是以扩展卡尔曼滤波（EKF）为代表的滤波方法，
一种是以图优化为代表的非线性优化方法。

滤波的方法中常见的是扩展卡尔曼滤波、粒子滤波、信息滤波等，这类SLAM问题是递增的、实时的处理数据并矫正机器人位姿。
基于粒子滤波的SLAM的处理思路是假设机器人知道当前时刻的位姿，利用编码器或者IMU之类的惯性导航又能够计算下一时刻的位姿，然而这类传感器有累计误差，所以再将每个粒子的激光传感器数据或者图像特征对比当前建立好的地图中的特征，挑选和地图特征匹配最好的粒子的位姿当做当前位姿，如此往复。当然在gmapping、hector_slam这类算法中，不会如此轻易的使用激光数据，激光测距这么准，当然不能只用来计算粒子权重，而是将激光数据与地图环境进行匹配（scan match）估计机器人位姿，比用编码器之流精度高出很多。

目前SLAM主流研究热点几乎都是基于图优化的，这和传感器有很大关系，以前使用激光构建二维的地图，现在研究热点都是用单目、双目、RGB-D构建地图。处理视觉SLAM如果用EKF，随着时间推移地图扩大，内存消耗，计算量都很大；而使用图优化计算在高建图精度的前提下效率还快。关于filter 和 graph 两类方法在visual slam里的对比可以参见《visual slam: why filter?》，不是说激光SLAM就不能用图优化，也可以。

在图优化的方法中（graph-based slam），处理数据的方式就和滤波的方法不同，它不是在线的纠正位姿，而是把所有数据记下来，最后一次性算账。

滤波方法的优缺点：
优点：在当时计算资源受限、待估计量比较简单的情况下，EKF为代表的滤波方法比较有效，经常用在激光SLAM中。
缺点：存储量和状态量是平方增长关系，因为存储的是协方差矩阵，因此不适合大型场景。而现在基于视觉的SLAM方案，路标点（特征点）数据很大，滤波方法根本吃不消，所以此时滤波的方法效率非常低。

g2o(General Graphic Optimization,G2O)
基于图优化的库，图优化是一种将非线性优化与图论结合起来的理论。
一个图由若干个顶点（vertex），以及连接这些顶点的边（edge）组成。
顶点是待优化的变量，边通常表示误差项。

三角形表示相机位姿节点,用圆形表示路标点,它们构成了图优化的顶点;
蓝色线表示相机的运动模型,红色虚线表示观测模型,它们构成了图优化的边。
节点为优化变量,边为误差项。

G2O基本框架结构

SparseOptimizer是整个图的核心
SparseOptimizer是一个Optimizable Graph
也是一个超图（HyperGraph）

超图包含了许多顶点（HyperGraph::Vertex）和边（HyperGraph::Edge）
而这些顶点继承自 Base Vertex，也就是OptimizableGraph::Vertex
而边可以继承自 BaseUnaryEdge（单边）, BaseBinaryEdge（双边）或BaseMultiEdge（多边），它们都叫做OptimizableGraph::Edge

整个图的核心SparseOptimizer 包含一个优化算法（OptimizationAlgorithm）的对象
OptimizationAlgorithm是通过OptimizationWithHessian来实现的
其中迭代策略可以从
Gauss-Newton（高斯牛顿法，简称GN）,
Levernberg-Marquardt（简称LM法）,
Powell’s dogleg 三者中间选择一个（我们常用的是GN和LM）

OptimizationWithHessian 内部包含一个求解器（Solver），这个Solver实际是由一个BlockSolver组成的。
这个BlockSolver有两个部分，
一个是SparseBlockMatrix ，用于计算稀疏的雅可比和Hessian矩阵；
一个是线性方程的求解器（LinearSolver），它用于计算迭代过程中最关键的一步HΔx=−b，
LinearSolver有几种方法可以选择：PCG, CSparse, Choldmod。

G2O图优化的流程

1、g2o的线性求解器LinearSolver

求增量方程：H△X=-b，方法就是直接求逆得到△X=-H.inv*b。

LinearSolverCholmod//使用sparse cholesky分解法。继承自LinearSolverCCS
LinearSolverCSparse//使用CSparse法。继承自LinearSolverCCS
LinearSolverPCG//使用preconditioned conjugate gradient 法，继承自LinearSolver
LinearSolverDense//使用dense cholesky分解法。继承自LinearSolver
LinearSolverEigen//依赖项只有eigen，使用eigen中sparse Cholesky 求解，因此编译好后可以方便的在其他地方使用，性能和CSparse差不多。继承自LinearSolver

2、 g2o的块求解器BlockSolver

BlockSolver有两种定义方式：

一种是指定的固定变量的solver

using BlockSolverPL = BlockSolver< BlockSolverTraits<p, l> >;

其中p代表pose的维度（注意一定是流形manifold下的最小表示），l表示landmark的维度

另一种是可变尺寸的solver
using BlockSolverX = BlockSolverPL;

BlockSolver_6_3 ：表示pose是6维，观测点是3维。用于3D SLAM中的BA
BlockSolver_7_3：在BlockSolver_6_3的基础上多了一个scale
BlockSolver_3_2：表示pose是3维，观测点是2维

template <int _PoseDim, int _LandmarkDim>
struct BlockSolverTraits
//variable size solver
typedef BlockSolver< BlockSolverTraits<Eigen::Dynamic, Eigen::Dynamic> > BlockSolverX;
// solver for BA/3D SLAM
typedef BlockSolver< BlockSolverTraits<6, 3> > BlockSolver_6_3;// 表示pose 是6维，观测点是3维。用于3D SLAM中的BA
// solver fo BA with scale
typedef BlockSolver< BlockSolverTraits<7, 3> > BlockSolver_7_3;// 在BlockSolver_6_3 的基础上多了一个scale  
// 2Dof landmarks 3Dof poses
typedef BlockSolver< BlockSolverTraits<3, 2> > BlockSolver_3_2;// 表示pose 是3维，观测点是2维

3、g2o的solver总求解器

OptimizationAlgorithm是通过OptimizationWithHessian 来实现的。其中迭代策略可以从Gauss-Newton（高斯牛顿法，简称GN）, Levernberg-Marquardt（简称LM法）, Powell’s dogleg 三者中间选择一个（我们常用的是GN和LM）

g2o::OptimizationAlgorithmGaussNewton// 高斯牛顿
g2o::OptimizationAlgorithmLevenberg//列文伯格马尔夸特
g2o::OptimizationAlgorithmDogleg//狗腿

4、g2o的SparseOptimizer稀疏优化器

SparseOptimizer是整个图的核心，是Optimizable Graph，也是一个超图（HyperGraph）

g2o::SparseOptimizer optimizer;//创建稀疏优化器
SparseOptimizer::setAlgorithm(OptimizationAlgorithm* algorithm)//用前面定义好的求解器作为求解方法
SparseOptimizer::setVerbose(bool verbose)//其中setVerbose是设置优化过程输出信息用的

5、添加图的顶点和边到SparseOptimizer

自定义顶点

HyperGraph::Vertex 是个abstract vertex，必须通过派生来使用
HyperGraph::Vertex 是通过类OptimizableGraph 来继承的
顶点的基类型是 BaseVertex模板类：BaseVertex， 参数 D 和 T，
D是int 类型的，表示vertex的最小维度，比如3D空间中旋转是3维的，那么这里 D = 3
T是待估计vertex的数据类型，比如用四元数表达三维旋转的话，T就是Quaternion 类型

代码示例：

VertexSE2 : public BaseVertex<3, SE2>  //2D pose Vertex, (x,y,theta)
//6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion)
VertexSE3 : public BaseVertex<6, Isometry3>  
VertexPointXY : public BaseVertex<2, Vector2>
VertexPointXYZ : public BaseVertex<3, Vector3>
VertexSBAPointXYZ : public BaseVertex<3, Vector3>
// SE3 Vertex parameterized internally with a transformation matrix and externally with its exponential map
VertexSE3Expmap : public BaseVertex<6, SE3Quat>
// SBACam Vertex, (x,y,z,qw,qx,qy,qz),(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
// qw is assumed to be positive, otherwise there is an ambiguity in qx,qy,qz as a rotation
VertexCam : public BaseVertex<6, SBACam>
// Sim3 Vertex, (x,y,z,qw,qx,qy,qz),7d vector,(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
VertexSim3Expmap : public BaseVertex<7, Sim3>

重新定义顶点一般需要考虑重写如下函数：

virtual void setToOriginImpl();
virtual void oplusImpl(const number_t* update);
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;

setToOriginImpl：顶点重置函数，设定被优化变量的原始值，一般置零。
oplusImpl：顶点更新函数，用于优化过程中增量△x 的计算根据增量方程计算出增量之后，通过这个函数对估计值进行调整。
read，write：分别是读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅仅声明一下就可以

优化变量SE3Quat是g2o定义的相机位姿类型，对应李群李代的变换矩阵。
它内部使用了四元数表达旋转，然后加上位移来存储位姿，同时支持李代数上的运算，比如对数映射（log函数）、李代数上增量（update函数）等操作。

相机位姿顶点类VertexSE3Expmap使用了李代数表示相机位姿，而不是使用旋转矩阵和平移矩阵
因为旋转矩阵是有约束的矩阵，它必须是正交矩阵且行列式为1。
使用它作为优化变量就会引入额外的约束条件，从而增大优化的复杂度。
而将旋转矩阵通过李群-李代数之间的转换关系转换为李代数表示，就可以把位姿估计变成无约束的优化问题，求解难度降低。

自定义边

BaseUnaryEdge，BaseBinaryEdge，BaseMultiEdge 分别表示一元边，两元边，多元边。
一元边你可以理解为一条边只连接一个顶点，
两元边理解为一条边连接两个顶点，也就是我们常见的边啦，
多元边理解为一条边可以连接多个（3个以上）顶点。

D 是 int 型表示测量值的维度 （dimension）
E 表示测量值的数据类型
VertexXi，VertexXj 分别表示不同顶点的类型

比如我们用边表示三维点投影到图像平面的重投影误差，就可以设置输入参数如下：

BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>

首先这个是个二元边。第1个2是说测量值是2维的，也就是图像像素坐标x,y的差值，对应测量值的类型是Vector2D，
两个顶点也就是优化变量分别是三维点 VertexSBAPointXYZ，和李群位姿VertexSE3Expmap

边主要有以下几个重要的成员函数

virtual void computeError();
virtual void linearizeOplus();
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;

computeError函数：计算真实值与估计值之间的误差函数。
linearizeOplus函数：计算该误差函数对优化变量的偏导数。
read，write：分别是读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅仅声明一下就可以

_measurement：存储观测值
_error：存储computeError() 函数计算的误差
_vertices[]：存储顶点信息，比如二元边的话，_vertices[] 的大小为2，存储顺序和调用setVertex(int, vertex) 是设定的int 有关（0 或1）
setId(int)：来定义边的编号（决定了在H矩阵中的位置）
setMeasurement(type) 定义观测值
setVertex(int, vertex) 定义顶点
setInformation() 定义协方差矩阵的逆

6、设置优化参数执行优化

设置SparseOptimizer的初始化、迭代次数、保存结果等。
SparseOptimizer::initializeOptimization(HyperGraph::EdgeSet& eset)//初始化
SparseOptimizer::optimize(int iterations, bool online)//设置迭代次数，然后就开始执行图优化了。

代码示例

g2o/types/sba/types_six_dof_expmap.h
//继承了BaseBinaryEdge类，观测值是2维，类型Vector2D,顶点分别是三维点、李群位姿
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    //1. 默认初始化
    EdgeProjectXYZ2UV();
    //2. 计算误差
    void computeError()  {
      //李群相机位姿v1
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
      // 顶点v2
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
      //相机参数
      const CameraParameters * cam
        = static_cast<const CameraParameters *>(parameter(0));
     //误差计算，测量值减去估计值，也就是重投影误差obs-cam
     //估计值计算方法是T*p,得到相机坐标系下坐标，然后在利用camera2pixel()函数得到像素坐标。
      Vector2D obs(_measurement);
      //误差 = 观测 - 投影
      _error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
    }
    //3. 线性增量函数，也就是雅克比矩阵J的计算方法
    virtual void linearizeOplus();
    //4. 相机参数
    CameraParameters * _cam; 
    bool read(std::istream& is);
    bool write(std::ostream& os) const;
};

cam_map 函数，定义在g2o/types/sba/types_six_dof_expmap.cpp
cam_map 函数功能是把相机坐标系下三维点（输入）用内参转换为图像坐标（输出）
Vector2  CameraParameters::cam_map(const Vector3 & trans_xyz) const {
  Vector2 proj = project2d(trans_xyz);
  Vector2 res;
  res[0] = proj[0]*focal_length + principle_point[0];
  res[1] = proj[1]*focal_length + principle_point[1];
  return res;
}
.map函数的功能是把世界坐标系下三维点变换到相机坐标系在g2o/types/sim3/sim3.h
      Vector3 map (const Vector3& xyz) const {
        return s*(r*xyz) + t;
      }
因此下面这个代码
v1->estimate().map(v2->estimate())
就是用V1估计的pose把V2代表的三维点，变换到相机坐标系下。

第六讲g2o_curve_fitting初始化BlockSolver

// 视觉SLAM十四讲第一版第六讲代码
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;// 每个误差项优化变量维度为3，误差值维度为1
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器
Block* solver_ptr = new Block( linearSolver );// 矩阵块求解器
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );

// 视觉SLAM十四讲第二版第六讲代码
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;// 每个误差项优化变量维度为3，误差值维度为1
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;// 线性求解器类型
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

第七讲pose_estimation_3d2d初始化BlockSolver

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d2d.cpp
typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>(); // 线性方程求解器
Block* solver_ptr = new Block ( linearSolver );// 矩阵块求解器
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );


// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d2d.cpp
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;  // pose is 6, landmark is 3
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

第七讲pose_estimation_3d3d初始化BlockSolver

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d3d.cpp
typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose维度为 6, landmark 维度为 3
Block::LinearSolverType* linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>(); // 线性方程求解器
Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );

// // 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d3d.cpp
typedef g2o::BlockSolverX BlockSolverType;
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
auto solver = new g2o::OptimizationAlgorithmLevenberg(
  g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));

g2o源码中顶点(优化变量)的定义

顶点（HyperGraph::Vertex）继承自 Base Vertex，也就是OptimizableGraph::Vertex

static const int Dimension = D; // dimension of the estimate (minimal) in the manifold space
//优化变量的维度，在流形空间（manifold）的最小表示
typedef T EstimateType;
EstimateType _estimate;
// T是顶点优化变量的类型
// 注意上面是参数类型含义
VertexSE2 : public BaseVertex<3, SE2>//2D pose Vertex, (x,y,theta)
VertexSE3 : public BaseVertex<6, Isometry3>//6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion)
VertexPointXY : public BaseVertex<2, Vector2>
VertexPointXYZ : public BaseVertex<3, Vector3>
VertexSBAPointXYZ : public BaseVertex<3, Vector3>

// SE3 Vertex parameterized internally with a transformation matrix and externally with its exponential map
VertexSE3Expmap : public BaseVertex<6, SE3Quat>

// SBACam Vertex, (x,y,z,qw,qx,qy,qz),(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
// qw is assumed to be positive, otherwise there is an ambiguity in qx,qy,qz as a rotation
VertexCam : public BaseVertex<6, SBACam>

// Sim3 Vertex, (x,y,z,qw,qx,qy,qz),7d vector,(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
VertexSim3Expmap : public BaseVertex<7, Sim3>

自定义顶点

自定义顶点主要写下面两个函数

virtual void setOriginImpl()// 优化变量的初始值
{
    _estimate = Type();
}
virtual void oplusImpl(const double* update) override// 优化变量更新函数
{
    _estimate += /*update*/;
}

第六讲g2o_curve_fitting自定义顶点

// 视觉SLAM十四讲第一版第六讲代码
// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>{
public:
    virtual void setToOriginImpl(){//设定被优化变量的原始值
        _estimate << 0,0,0;
    }
    virtual void oplusImpl( const double* update ){//优化过程中增量△x的计算,根据增量方程计算出增量之后，通过这个函数对估计值进行调整
        _estimate += Eigen::Vector3d(update);
    }
};
// 视觉SLAM十四讲第二版第六讲代码
// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> {
public:
  virtual void setToOriginImpl() override {// 重置
    _estimate << 0, 0, 0;
  }
  virtual void oplusImpl(const double *update) override {// 更新
    _estimate += Eigen::Vector3d(update);
  }
};

第七讲代码 pose_estimation_3d2d.cpp自定义顶点

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d2d.cpp
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();
  }
  // left multiplication on SE3
  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
  }
};

第七讲代码 pose_estimation_3d3d.cpp自定义顶点

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d3d.cpp
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();
  }
  // left multiplication on SE3
  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
  }
};

g2o/types/sba/types_six_dof_expmap.h

第一个参数6 表示内部存储的优化变量维度，这是个6维的李代数
第二个参数是优化变量的类型，这里使用了g2o定义的相机位姿类型：SE3Quat
具体查看g2o/types/slam3d/se3quat.h
它内部使用了四元数表达旋转，然后加上位移来存储位姿，同时支持李代数上的运算，比如对数映射（log函数）、李代数上增量（update函数）等操作

class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
  VertexSE3Expmap();
  
  virtual void setToOriginImpl() {
    _estimate = SE3Quat();
  }

  virtual void oplusImpl(const number_t* update_)  {
    Eigen::Map<const Vector6> update(update_);
    setEstimate(SE3Quat::exp(update)*estimate());//更新方式
  }
};

三维点

空间点位置 VertexPointXYZ，维度为3，类型是Eigen的Vector3

class G2O_TYPES_SBA_API VertexSBAPointXYZ : public BaseVertex<3, Vector3>{
    VertexSBAPointXYZ();
    
    virtual void setToOriginImpl() {
      _estimate.fill(0);
    }

    virtual void oplusImpl(const number_t* update){
      Eigen::Map<const Vector3> v(update);
      _estimate += v;
    }
};

向图中添加顶点

第六讲g2o_curve_fitting向图中添加顶点

// 视觉SLAM十四讲第一版第六讲代码
CurveFittingVertex* v = new CurveFittingVertex();
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );

// 视觉SLAM十四讲第二版第六讲代码
CurveFittingVertex *v = new CurveFittingVertex();
v->setEstimate(Eigen::Vector3d(ae, be, ce));
v->setId(0);
optimizer.addVertex(v);

第七讲pose_estimation_3d2d向图中添加顶点

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d2d.cpp
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
Eigen::Matrix3d R_mat;
R_mat <<　R.at<double> ( 0,0 ), R.at<double> ( 0,1 ), R.at<double> ( 0,2 ),
         R.at<double> ( 1,0 ), R.at<double> ( 1,1 ), R.at<double> ( 1,2 ),
         R.at<double> ( 2,0 ), R.at<double> ( 2,1 ), R.at<double> ( 2,2 );
pose->setId ( 0 );
pose->setEstimate ( g2o::SE3Quat (
                        R_mat,
                        Eigen::Vector3d ( t.at<double> ( 0,0 ), t.at<double> ( 1,0 ), t.at<double> ( 2,0 ) )
                    ) );
optimizer.addVertex ( pose );

int index = 1;
  for ( const Point3f p:points_3d )   // landmarks
  {
      g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
      point->setId ( index++ );
      point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
      point->setMarginalized ( true ); // g2o 中必须设置 marg 参见第十讲内容
      optimizer.addVertex ( point );
  }

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d2d.cpp
VertexPose *vertex_pose = new VertexPose(); // camera vertex_pose
vertex_pose->setId(0);
vertex_pose->setEstimate(Sophus::SE3d());
optimizer.addVertex(vertex_pose);

第七讲pose_estimation_3d3d向图中添加顶点

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d3d.cpp
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
pose->setId(0);
pose->setEstimate( g2o::SE3Quat(
    Eigen::Matrix3d::Identity(),
    Eigen::Vector3d( 0,0,0 )
) );
optimizer.addVertex( pose );

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d3d.cpp
VertexPose *pose = new VertexPose(); // camera pose
pose->setId(0);
pose->setEstimate(Sophus::SE3d());
optimizer.addVertex(pose);

g2o源码中边(误差方程)的定义

边（HyperGraph::Edge）继承自 BaseUnaryEdge（单边）, BaseBinaryEdge（双边）或BaseMultiEdge（多边），都叫做OptimizableGraph::Edge
一元边你可以理解为一条边只连接一个顶点，顶点无顺序
两元边理解为一条边连接两个顶点，顶点有顺序，０只能是路标，１只能是位姿
多元边理解为一条边可以连接多个（3个以上）顶点
参数：D, E, VertexXi, VertexXj，
D 是 int 型，表示测量值的维度 （dimension）
E 表示测量值的数据类型
VertexXi，VertexXj 分别表示不同顶点的类型

 BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>//用边表示三维点投影到图像平面的重投影误差

第1个2是说测量值是2维的，也就是图像像素坐标x,y的差值，对应测量值的类型是Vector2D，
两个顶点也就是优化变量分别是三维点 VertexSBAPointXYZ，和李群位姿VertexSE3Expmap

自定义边

virtual void computeError();//当前顶点优化变量的测量值与真实值之间的误差
virtual void linearizeOplus();//误差对优化变量的偏导数也就是Jacobian

几个重要的成员变量和函数

_measurement// 存储观测值
_error// 存储computeError()函数计算的误差
_vertices[]// 存储顶点的信息，比如二元边的话，_vertices[] 的大小为2，存储顺序和调用setVertex(int, vertex) 是设定的int 有关（0 或1）
setId(int)// 定义边的编号（决定了在H矩阵中的位置）
setMeasurement(type)// 定义观测值
setVertex(int, vertex)// 定义顶点
setInformation() //定义协方差矩阵的逆

曲线拟合g2o_curve_fitting自定义边

// 视觉SLAM十四讲第一版第六讲代码
// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>{
public:
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    void computeError(){//计算当前顶点计算的测量值与真实测量值之间的误差
        const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);//类型转换
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
public:
    double _x;  // x 值
};

// 视觉SLAM十四讲第二版第六讲代码
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
  CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
  // 计算曲线模型误差
  virtual void computeError() override {
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    const Eigen::Vector3d abc = v->estimate();
    _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
  }
  virtual void linearizeOplus() override {// 对优化变量求偏导数，计算雅可比矩阵
    const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
    const Eigen::Vector3d abc = v->estimate();
    double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
    _jacobianOplusXi[0] = -_x * _x * y;
    _jacobianOplusXi[1] = -_x * y;
    _jacobianOplusXi[2] = -y;
  }
public:
  double _x;  // x 值

第七讲pose_estimation_3d2d自定义边

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d2d.cpp
class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
  EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}
  virtual void computeError() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_pixel = _K * (T * _pos3d);
    pos_pixel /= pos_pixel[2];
    _error = _measurement - pos_pixel.head<2>();
  }

  virtual void linearizeOplus() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_cam = T * _pos3d;
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    _jacobianOplusXi
      << -fx / Z, 
      0, 
      fx * X / Z2, 
      fx * X * Y / Z2, 
      -fx - fx * X * X / Z2, 
      fx * Y / Z,
      0, 
      -fy / Z, 
      fy * Y / (Z * Z), 
      fy + fy * Y * Y / Z2, 
      -fy * X * Y / Z2, 
      -fy * X / Z;
  }

第七讲pose_estimation_3d3d自定义边

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d3d.cpp
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, g2o::VertexSE3Expmap>{
public:
    EdgeProjectXYZRGBDPoseOnly( const Eigen::Vector3d& point ) : _point(point) {}
    virtual void computeError(){
        const g2o::VertexSE3Expmap* pose = static_cast<const g2o::VertexSE3Expmap*> ( _vertices[0] );
        _error = _measurement - pose->estimate().map( _point );// measurement is p, point is p'
    }

    virtual void linearizeOplus(){
        g2o::VertexSE3Expmap* pose = static_cast<g2o::VertexSE3Expmap *>(_vertices[0]);
        g2o::SE3Quat T(pose->estimate());
        Eigen::Vector3d xyz_trans = T.map(_point);
        double x = xyz_trans[0];
        double y = xyz_trans[1];
        double z = xyz_trans[2];

        _jacobianOplusXi(0,0) = 0;
        _jacobianOplusXi(0,1) = -z;
        _jacobianOplusXi(0,2) = y;
        _jacobianOplusXi(0,3) = -1;
        _jacobianOplusXi(0,4) = 0;
        _jacobianOplusXi(0,5) = 0;

        _jacobianOplusXi(1,0) = z;
        _jacobianOplusXi(1,1) = 0;
        _jacobianOplusXi(1,2) = -x;
        _jacobianOplusXi(1,3) = 0;
        _jacobianOplusXi(1,4) = -1;
        _jacobianOplusXi(1,5) = 0;

        _jacobianOplusXi(2,0) = -y;
        _jacobianOplusXi(2,1) = x;
        _jacobianOplusXi(2,2) = 0;
        _jacobianOplusXi(2,3) = 0;
        _jacobianOplusXi(2,4) = 0;
        _jacobianOplusXi(2,5) = -1;
    }
protected:
    Eigen::Vector3d _point;
};


// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d3d.cpp
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, VertexPose> {
public:
  EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}
  virtual void computeError() override {
    const VertexPose *pose = static_cast<const VertexPose *> ( _vertices[0] );
    _error = _measurement - pose->estimate() * _point;
  }
  virtual void linearizeOplus() override {
    VertexPose *pose = static_cast<VertexPose *>(_vertices[0]);
    Sophus::SE3d T = pose->estimate();
    Eigen::Vector3d xyz_trans = T * _point;
    _jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();
    _jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);
  }
protected:
  Eigen::Vector3d _point;
};

https://github.com/RainerKuemmerle/g2o/tree/master/g2o/types/sba/types_six_dof_expmap.h

//继承了BaseBinaryEdge类，观测值是2维，类型Vector2D,顶点分别是三维点、李群位姿
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{
    //1. 默认初始化
    EdgeProjectXYZ2UV();
    //2. 计算误差
    void computeError()  {
      //李群相机位姿v1
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
      // 顶点v2
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
      //相机参数
      const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));
     //误差计算，测量值减去估计值，也就是重投影误差obs-cam
     //估计值计算方法是T*p,得到相机坐标系下坐标，然后在利用camera2pixel()函数得到像素坐标。
      Vector2D obs(_measurement);
      _error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));// 误差 = 观测 - 投影|cam_map()函数借助内参把相机坐标系下三维点转换为图像坐标｜.map()函数借助位姿外参把世界坐标系下三维点变换到相机坐标系三维点(s*(r*xyz) + t)|v1->estimate().map(v2->estimate()用V1估计的pose把V2代表的三维点，变换到相机坐标系下。
    }
    //3. 线性增量函数，也就是雅克比矩阵J的计算方法
    virtual void linearizeOplus();
    //4. 相机参数
    CameraParameters * _cam; 

slambook/ch7/pose_estimation_3d2d.cpp误差方程和雅克比矩阵详细计算推导

上面是公式,下面是代码,接下来是详细的计算过程

virtual void linearizeOplus() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_cam = T * _pos3d;
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    _jacobianOplusXi
      << 
      -fx / Z, 
      0, 
      fx * X / Z2, 
      fx * X * Y / Z2, 
      -fx - fx * X * X / Z2, 
      fx * Y / Z,
      0, 
      -fy / Z, 
      fy * Y / (Z * Z), 
      fy + fy * Y * Y / Z2, 
      -fy * X * Y / Z2, 
      -fy * X / Z;
  }

对x, y, z撇分别求偏导数

slambook/ch7/pose_estimation_3d3d.cpp误差方程和雅克比矩阵详细计算推导

class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();
  }

  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
  }
};

VertexPose *pose = new VertexPose(); // camera pose
pose->setId(0);
pose->setEstimate(Sophus::SE3d());
optimizer.addVertex(pose);

class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, VertexPose> {
  EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}

  virtual void computeError() override {
    const VertexPose *pose = static_cast<const VertexPose *> ( _vertices[0] );
    _error = _measurement - pose->estimate() * _point;
  }

  virtual void linearizeOplus() override {
    VertexPose *pose = static_cast<VertexPose *>(_vertices[0]);
    Sophus::SE3d T = pose->estimate();
    Eigen::Vector3d xyz_trans = T * _point;
    _jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();
    _jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);// 李代数的反对称矩阵
  }
protected:
  Eigen::Vector3d _point;
};

for (size_t i = 0; i < pts1.size(); i++) {
  EdgeProjectXYZRGBDPoseOnly *edge = new EdgeProjectXYZRGBDPoseOnly(Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));
  edge->setVertex(0, pose);
  edge->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));
  edge->setInformation(Eigen::Matrix3d::Identity());
  optimizer.addEdge(edge);
}

_jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();
_jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);// 李代数的反对称矩阵

下图是这两句代码的理解

第八讲光流法雅克比矩阵详细推导

代码

// jacobian from se3 to u,v NOTE that in g2o the Lie algebra is (\omega, \epsilon), where \omega is so(3) and \epsilon the translation
virtual void linearizeOplus( ){
if ( level() == 1 ){
    _jacobianOplusXi = Eigen::Matrix<double, 1, 6>::Zero();
    return;
}
VertexSE3Expmap* vtx = static_cast<VertexSE3Expmap*> ( _vertices[0] );
Eigen::Vector3d xyz_trans = vtx->estimate().map ( x_world_ );   // q in book
double x = xyz_trans[0];
double y = xyz_trans[1];
double invz = 1.0/xyz_trans[2];
double invz_2 = invz*invz;

float u = x*fx_*invz + cx_;
float v = y*fy_*invz + cy_;

Eigen::Matrix<double, 2, 6> jacobian_uv_ksai;

jacobian_uv_ksai ( 0,0 ) = - x*y*invz_2 *fx_;
jacobian_uv_ksai ( 0,1 ) = ( 1+ ( x*x*invz_2 ) ) *fx_;
jacobian_uv_ksai ( 0,2 ) = - y*invz *fx_;
jacobian_uv_ksai ( 0,3 ) = invz *fx_;
jacobian_uv_ksai ( 0,4 ) = 0;
jacobian_uv_ksai ( 0,5 ) = -x*invz_2 *fx_;

jacobian_uv_ksai ( 1,0 ) = - ( 1+y*y*invz_2 ) *fy_;
jacobian_uv_ksai ( 1,1 ) = x*y*invz_2 *fy_;
jacobian_uv_ksai ( 1,2 ) = x*invz *fy_;
jacobian_uv_ksai ( 1,3 ) = 0;
jacobian_uv_ksai ( 1,4 ) = invz *fy_;
jacobian_uv_ksai ( 1,5 ) = -y*invz_2 *fy_;

Eigen::Matrix<double, 1, 2> jacobian_pixel_uv;
jacobian_pixel_uv ( 0,0 ) = ( getPixelValue ( u+1,v )-getPixelValue ( u-1,v ) ) /2;
jacobian_pixel_uv ( 0,1 ) = ( getPixelValue ( u,v+1 )-getPixelValue ( u,v-1 ) ) /2;
_jacobianOplusXi = jacobian_pixel_uv*jacobian_uv_ksai;
}

第九讲0.3误差方程和雅克比矩阵

class EdgeProjectXYZ2UVPoseOnly: public g2o::BaseUnaryEdge<2, Eigen::Vector2d, g2o::VertexSE3Expmap >{
virtual void computeError(){
    const g2o::VertexSE3Expmap* pose = static_cast<const g2o::VertexSE3Expmap*> ( _vertices[0] );
    error = _measurement - camera_->camera2pixel ( pose->estimate().map(point_) );
}

virtual void linearizeOplus(){
    g2o::VertexSE3Expmap* pose = static_cast<g2o::VertexSE3Expmap*> ( _vertices[0] );
    g2o::SE3Quat T ( pose->estimate() );
    Vector3d xyz_trans = T.map ( point_ );
    double x = xyz_trans[0];
    double y = xyz_trans[1];
    double z = xyz_trans[2];
    double z_2 = z*z;

    _jacobianOplusXi ( 0,0 ) =  x*y/z_2 *camera_->fx_;
    _jacobianOplusXi ( 0,1 ) = - ( 1+ ( x*x/z_2 ) ) *camera_->fx_;
    _jacobianOplusXi ( 0,2 ) = y/z * camera_->fx_;
    _jacobianOplusXi ( 0,3 ) = -1./z * camera_->fx_;
    _jacobianOplusXi ( 0,4 ) = 0;
    _jacobianOplusXi ( 0,5 ) = x/z_2 * camera_->fx_;

    _jacobianOplusXi ( 1,0 ) = ( 1+y*y/z_2 ) *camera_->fy_;
    _jacobianOplusXi ( 1,1 ) = -x*y/z_2 *camera_->fy_;
    _jacobianOplusXi ( 1,2 ) = -x/z *camera_->fy_;
    _jacobianOplusXi ( 1,3 ) = 0;
    _jacobianOplusXi ( 1,4 ) = -1./z *camera_->fy_;
    _jacobianOplusXi ( 1,5 ) = y/z_2 *camera_->fy_;
    }
    Vector3d point_;
    Camera* camera_;
};

g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap();
pose->setId ( 0 );
pose->setEstimate ( g2o::SE3Quat (
    T_c_r_estimated_.rotation_matrix(), 
    T_c_r_estimated_.translation()
) );
optimizer.addVertex ( pose );

// edges
for ( int i=0; i<inliers.rows; i++ ){
    int index = inliers.at<int>(i,0);
    // 3D -> 2D projection
    EdgeProjectXYZ2UVPoseOnly* edge = new EdgeProjectXYZ2UVPoseOnly();
    edge->setId(i);
    edge->setVertex(0, pose);
    edge->camera_ = curr_->camera_.get();
    edge->point_ = Vector3d( pts3d[index].x, pts3d[index].y, pts3d[index].z );
    edge->setMeasurement( Vector2d(pts2d[index].x, pts2d[index].y) );
    edge->setInformation( Eigen::Matrix2d::Identity() );
    optimizer.addEdge( edge );
}

向图中添加边

第六讲曲线拟合g2o_curve_fitting向图中添加边

// 视觉SLAM十四讲第一版第六讲代码
for ( int i=0; i<N; i++ ){
    CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
    edge->setId(i);
    edge->setVertex(0, v);//设置连接的顶点
    edge->setMeasurement(y_data[i]);//观测数值
    edge->setInformation(Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma)); //信息矩阵：协方差矩阵之逆
    optimizer.addEdge( edge );
}

// 视觉SLAM十四讲第二版第六讲代码
for (int i = 0; i < N; i++) {
    CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
    edge->setId(i);
    edge->setVertex(0, v);                // 设置连接的顶点
    edge->setMeasurement(y_data[i]);      // 观测数值
    edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma)); // 信息矩阵：协方差矩阵之逆
    optimizer.addEdge(edge);
}

第七讲pose_estimation_3d2d向图中添加边

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d2d.cpp
index = 1;
for ( const Point2f p:points_2d ){
    g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
    edge->setId ( index );
    edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );// 三维点　_vertices[0] 对应的是 VertexSBAPointXYZ 类型的顶点，也就是三维点，const VertexSBAPointXYZ* v2 = static_cast(_vertices[0]);// 顶点v2
    edge->setVertex ( 1, pose );// 位姿　_vertices[1] 对应的是VertexSE3Expmap 类型的顶点，也就是位姿pose。const VertexSE3Expmap* v1 = static_cast(_vertices[1]); //李群相机位姿v1
    edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );// 视觉SLAM的观测是特征点的图像坐标(x,y)
    edge->setParameterId ( 0,0 );
    edge->setInformation ( Eigen::Matrix2d::Identity() );
    optimizer.addEdge ( edge );
    index++;
}

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d2d.cpp
Eigen::Matrix3d K_eigen;
K_eigen <<
        K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),
  K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),
  K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);
int index = 1;
for (size_t i = 0; i < points_2d.size(); ++i) {
  auto p2d = points_2d[i];
  auto p3d = points_3d[i];
  EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
  edge->setId(index);
  edge->setVertex(0, vertex_pose);
  edge->setMeasurement(p2d);
  edge->setInformation(Eigen::Matrix2d::Identity());
  optimizer.addEdge(edge);
  index++;
}

第七讲代码pose_estimation_3d3d向图中添加边

// 视觉SLAM十四讲第一版第七讲代码 pose_estimation_3d3d.cpp
int index = 1;
vector<EdgeProjectXYZRGBDPoseOnly*> edges;
for ( size_t i=0; i<pts1.size(); i++ ){
    EdgeProjectXYZRGBDPoseOnly* edge = new EdgeProjectXYZRGBDPoseOnly(
        Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z) );
    edge->setId( index );
    edge->setVertex( 0, dynamic_cast<g2o::VertexSE3Expmap*> (pose) );
    edge->setMeasurement( Eigen::Vector3d(
        pts1[i].x, pts1[i].y, pts1[i].z) );
    edge->setInformation( Eigen::Matrix3d::Identity()*1e4 );
    optimizer.addEdge(edge);
    index++;
    edges.push_back(edge);
}

// 视觉SLAM十四讲第二版第七讲代码 pose_estimation_3d3d.cpp
for (size_t i = 0; i < pts1.size(); i++) {
  EdgeProjectXYZRGBDPoseOnly *edge = new EdgeProjectXYZRGBDPoseOnly(
    Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));
  edge->setVertex(0, pose);
  edge->setMeasurement(Eigen::Vector3d(
    pts1[i].x, pts1[i].y, pts1[i].z));
  edge->setInformation(Eigen::Matrix3d::Identity());
  optimizer.addEdge(edge);
}

g2o_viewer

安装依赖项： sudo apt-get install libqglviewer-dev-qt4
find_package(Qt5 COMPONENTS Core Xml OpenGL Gui Widgets)
安装qt5的之前首先删除qt4：
sudo apt-get remove qt4-qmake # 举个例子的删除qt4-qmake
sudo apt-get install qt5-default qtcreator
然后安装gl的依赖：
sudo apt-get install libqglviewer-dev
sudo ldconfig
ldconfig是一个程序，位于/sbin下，是root用户使用的东东。具体作用及用法可以man ldconfig查到简单的说，它的作用就是将/etc/ld.so.conf列出的路径下的库文件 缓存到/etc/ld.so.cache 以供使用,因此当安装完一些库文件，(例如刚安装好glib)，或者修改ld.so.conf增加新的库路径后，需要运行一下/sbin/ldconfig使所有的库文件都被缓存到ld.so.cache中，如果没做，即使库文件明明就在/usr/lib下的，也是不会被使用的，结果编译过程中抱错，缺少xxx库，去查看发现明明就在那放着，搞的想大骂computer蠢猪一个。
https://blog.csdn.net/oathevil/article/details/13564213

重新编译g2o

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/city10000/originalDataset/city10000.g2o

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/intel/originalDataset

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/intel/originalDataset/intel.g2o 

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/manhattan/originalDataset/g2o/manhattanOlson3500.g2o

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/manhattan/originalDataset/Olson/manhattanOlson3500.g2o

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/ring/originalDataset/ring.g2o

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/ringCity/originalDataset/ringCity.g2o

~/slambook/3rdparty/g2o/bin$ g2o_viewer /home/openslam_vertigo-master/datasets/sphere2500/originalDataset/sphere2500.g2o