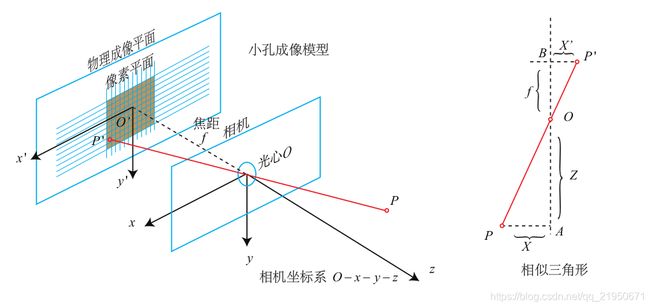
【视觉SLAM十四讲源码解读】坐标变换 像素坐标系、图像坐标系、相机坐标系、相机归一化坐标系、世界坐标系

什么是世界坐标系

世界坐标系是为了描述相机的位置而被引入的，平移向量T是第一个坐标原点与第二个坐标原点的偏移量；
世界坐标系（Ow，以空间一点为原点）

世界坐标系（world coordinate）(xw,yw,zw)，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。

什么是相机坐标系

相机坐标系（Oc以小孔即光心为原点） (Xc,Yc,Zc)至图像坐标系(x,y)
根据小孔成像原理，图像坐标系应在相机坐标系的另一边，为倒立反向成像，但为方便理解和计算，故投影至同侧。

相机坐标系（camera coordinate）(xc,yc,zc)，也是一个三维直角坐标系，原点位于镜头光心处，x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。

什么是图像物理坐标系

成像平面坐标系(x,y)：像素坐标系不利于坐标变换，因此需要建立图像坐标系XOY，其坐标轴的单位通常为毫米（mm），原点是相机光轴与相面的交点（称为主点），即图像的中心点，X轴、Y轴分别与u轴、v轴平行。故两个坐标系实际是平移关系，即可以通过平移就可得到。
图像物理坐标系（O1以像平面中心为原点）

什么是像素坐标系

像素坐标系uov是一个二维直角坐标系，反映了相机CCD/CMOS芯片中像素的排列情况。原点o位于图像的左上角，u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素（整数）。
图像像素坐标系（O以像平面左下角为原点）

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm，即1pixel=dx mm

重点就是u0和v0的值是在像素坐标系下的中心像素，比如600*400，那坐标就是(300，200)
所以才可以有下面的加法

伸缩变换及平移变换

四个坐标系之间存在着下述关系 ( 矩阵依次左乘 )


一个三维中的坐标点，的确可以在图像中找到一个对应的像素点，但是反过来，通过图像中的一个点找到它在三维中对应的点就很成了一个问题，因为我们并不知道等式左边的Zc的值。

光心是什么

可以把凸透镜的几何中心近似看作是光心，因为实际上两者不重合，所以才径向和切向畸变。

焦距是什么

是成像平面或者像素平面和光心之间的距离，焦距越大，人细节越清楚，视角越小；焦距越小，视野越广，但细节越看不清。

总结五种坐标系的关系

按照十四讲的顺序我们首先接触的是像素坐标系、图像坐标系、相机坐标系、相机归一化坐标系、世界坐标系，这里学着学着就蒙了，所以我建议先学习投影模型，我认为二者可以理解为互逆过程，总结一下就是世界坐标和相机坐标之间要借助外参就是Rt进行转换，相机和相机归一化之间要有一个尺度的转换，这里默认尺度是Z，这里正是三维变为二维的过程，就像（10，４，２）和（５，２，１）一样忽略第三个维度，前两个维度是一样的。相机坐标系的原点是光心，图像坐标系的原点是焦点，焦点和关心之间的距离是焦距，两个相机光心之间的距离值是基线，基线乘fx除Z=视差，像素平面的原点是左上角和OpenCV的坐标系一样，像素平面和成像平面之间相差的是平移和缩放通过内参fx,fy,cx,cy实现。

五种坐标系转换原理

根据三角形相似原理得出下面的公式：

$\frac{Z}{f}$ = $\frac{X}{X^{\prime }}$ = $\frac{Y}{Y^{\prime }}$

整理一下得到成像平面点和现实世界空间点之间的关系：

$X^{\prime }$ = $f\ast \frac{X}{Z}$
$Y^{\prime }$ = $f\ast \frac{Y}{Z}$

假设$P^{\prime }$的像素坐标为:$[u,v{]}^T$

像素坐标系通常的定义方式是:

原点$o^{\prime }$位于图像的左上角,
$u$轴向右与$x$轴平行,
$v$轴向下与$y$轴平行。

像素坐标系与成像平面之间相差了一个缩放和一个原点的平移。

设像素坐标在$u$轴上缩放了$\alpha$倍,在$v$上缩放了$\beta$倍。

同时原点平移了$[c_x,c_y{]}^T$

那么$P^{\prime }$的坐标与像素坐标$[u,v{]}^T$的关系为:

$u$ = $\alpha \ast X^{\prime }+c_x$
$v$ = $\beta \ast Y^{\prime }+c_y$

$X^{\prime }$ = $\frac{u-c_x}{\alpha }$
$Y^{\prime }$ = $\frac{v-c_y}{\beta }$

并把$\alpha f$合并成$f_x$,把$\beta f$合并成$f_y$

结合上面成像平面点和现实世界空间点之间的关系

$X^{\prime }$ = $f\ast \frac{X}{Z}$
$Y^{\prime }$ = $f\ast \frac{Y}{Z}$

得到下面的像素点和空间点之间的关系

$u$ = $f_x\ast \frac{X}{Z}+c_x$

$v$ = $f_y\ast \frac{Y}{Z}+c_y$

$\frac{u-c_x}{f_x}\ast Z$ = $X$

$\frac{v-c_y}{f_y}\ast Z$ = $Y$

$f$的单位为米,

$\alpha$, $\beta$的单位为像素每米,

所以$f_x$, $f_y$的单位为像素。

把该式写成矩阵形式,会更加简洁,不过左侧需要用到齐次坐标:

$\triangleq$ 表示定义为，读作德尔塔等于或 Delta Equal To。

$\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)$ = $\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)$ $\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)$ $\triangleq$ $\frac{1}{Z}\times KP$

换一种写法

$\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)$ = $Z\times \left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_x& c_y\\ 0& 0& 1\end{array}\right)$ $\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)$ $\triangleq$ $KP$

中间的量组成的矩阵称为相机的内参数矩阵(Camera Intrinsics)K

上面我们使用的$P$是在相机坐标系下的坐标

由于相机在运动,所以$P$的相机坐标应该是它的世界坐标(记为$P_w$ ),

根据相机的当前位姿,变换到相机坐标系下的结果。

相机的位姿由它的旋转矩阵$R$和平移向量$t$来描述。

则有下面关系式:

$Z{P}_{uv}$=$Z\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$ = $K(R{P}_w+t)$= $KT{P}_w$

终于把理论部分说明白了。

这个是归一化平面的点(Z = 1)转化为像素坐标。

Vector2d Camera::camera2pixel ( const Vector3d& p_c )
{
    return Vector2d (
        fx_ * p_c ( 0,0 ) / p_c ( 2,0 ) + cx_,
        fy_ * p_c ( 1,0 ) / p_c ( 2,0 ) + cy_
    );
}

p_c ( 0,0 ) = $u$
p_c ( 1,0 ) = $v$
p_c ( 2,0 ) = 1

因为我们归一化左边用列向量表示了，所以是这样的
默认向量都用列向量表示，
所以书面写的时候才会加上一个装置的符号"T"
这个是上面公式的直接应用
成像平面点和现实世界空间点之间的关系：

$X^{\prime }$ = $f\ast \frac{X}{Z}$
$Y^{\prime }$ = $f\ast \frac{Y}{Z}$

成像平面的$p^{\prime }$的坐标与像素坐标$[u,v{]}^T$的关系为:

$u$ = $\alpha \ast X^{\prime }+c_x$
$v$ = $\beta \ast Y^{\prime }+c_y$

推导出

$u$ = $\alpha \ast f\ast \frac{X}{Z}+c_x$
$v$ = $\beta \ast f\ast \frac{Y}{Z}+c_y$

把$\alpha f$合并成$f_x$,把$\beta f$合并成$f_y$

$u$ = $f_x\ast \frac{X}{Z}+c_x$
$v$ = $f_y\ast \frac{Y}{Z}+c_y$

---

这个是像素点转换到相机坐标系下面的点

Vector3d Camera::pixel2camera ( const Vector2d& p_p, double depth )
{
    return Vector3d (
        ( p_p ( 0,0 )-cx_ ) *depth/fx_,
        ( p_p ( 1,0 )-cy_ ) *depth/fy_,
        depth
    );
}

理解：
p_p ( 0,0 ) = $u$
p_p ( 1,0 ) = $v$

那么$P^{\prime }$的坐标与像素坐标$[u,v{]}^T$的关系为:

$u$ = $\alpha \ast X^{\prime }+c_x$
$v$ = $\beta \ast Y^{\prime }+c_y$

首先推导出

$u-c_x$ = $\alpha \ast X^{\prime }$
$v-c_y$ = $\beta \ast Y^{\prime }$

然后推导出

$\frac{u-c_x}{\alpha }$ = $X^{\prime }$
$\frac{v-c_y}{\beta }$ = $Y^{\prime }$

成像平面点和现实世界空间点之间的关系：

$X^{\prime }$ = $f\ast \frac{X}{Z}$
$Y^{\prime }$ = $f\ast \frac{Y}{Z}$

推导出

$\frac{u-c_x}{\alpha }$ = $f\ast \frac{X}{Z}$
$\frac{v-c_y}{\beta }$ = $f\ast \frac{Y}{Z}$

$u-c_x$ = $\alpha \ast f\ast \frac{X}{Z}$
$v-c_y$ = $\beta \ast f\ast \frac{Y}{Z}$

把$\alpha f$合并成$f_x$
把$\beta f$合并成$f_y$

$u-c_x$ = $f_x\ast \frac{X}{Z}$

$v-c_y$ = $f_y\ast \frac{Y}{Z}$

---

$\frac{u-c_x}{f_x}$ = $\frac{X}{Z}$

$\frac{v-c_y}{f_y}$ = $\frac{Y}{Z}$

---

$\frac{u-c_x}{f_x}$ = $X^{\prime }$

$\frac{v-c_y}{f_y}$ = $Y^{\prime }$

乘上depth的原因，应该是因为下面这个公式

$\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)$ = $Z\times \left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)$ $\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)$ $\triangleq$ $KP$

就不太懂那个频繁用到的函数像素坐标转相机归一化坐标
Point2d pixel2cam(const Point2d &p, const Mat &K);

Vector3d Camera::pixel2camera ( const Vector2d& p_p, double depth )

对比一下

Point2d pixel2cam(const Point2d &p, const Mat &K) {
    cout << K.at<double>(0, 2) << endl;
  return Point2d
    (
      (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
      (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

首先相机内参数是这样的：

$\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)$

K.at(0, 2) = $c_x$
K.at(0, 0) = $f_x$
K.at(1, 2) = $c_y$
K.at(1, 1) = $f_y$

(p.x - $c_x$) / $f_x$
(p.y - $c_y$) / $f_y$

这刚好是上面代码推导出来的公式

$\frac{u-c_x}{f_x}$ = $X^{\prime }$

$\frac{v-c_y}{f_y}$ = $Y^{\prime }$

所以这个代买求的是成像平面的坐标 可能是省略了 Z=1 所以就是归一化平面坐标了

投影模型

１、世界坐标$P_w$ (路标点)通过外参数R t转换到相机坐标$P_c$

$P_w$ = $\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$

$P_c$ = $\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ Z^{\prime }\end{array}\right]$

$R\ast P_w+t$ = $P_c$

$R\ast \left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]+t$ = $\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ Z^{\prime }\end{array}\right]$

２、相机坐标系下的相机坐标$P_c$投影至相机坐标系下的归一化平面的相机坐标$P_c$

$P_c$ = $\left[\begin{array}{c}\frac{X^{\prime }}{Z^{\prime }}\\ \frac{Y^{\prime }}{Z^{\prime }}\\ \frac{Z^{\prime }}{Z^{\prime }}\end{array}\right]$

３、归一化平面的相机坐标$P_c$转换为像素坐标

假设$P_c$的像素坐标为:$\left[\begin{array}{c}u\\ v\end{array}\right]$

相机模型:相机坐标系下的三维点与成像平面之间通过三角形相似建立关系

$u$ = $f_x\ast \frac{X^{\prime }}{Z^{\prime }}+c_x$
$v$ = $f_y\ast \frac{Y^{\prime }}{Z^{\prime }}+c_y$

上述１、２、３、过程称为投影模型

world2camera世界坐标转化为相机坐标

Vector3d Camera::world2camera ( const Vector3d& p_w, const SE3& T_c_w )
{
    return T_c_w*p_w;
}

camera2world相机坐标转化为世界坐标

Vector3d Camera::camera2world ( const Vector3d& p_c, const SE3& T_c_w )
{
    return T_c_w.inverse() *p_c;
}

camera2pixel相机坐标系下面的点转化为像素坐标

Vector2d Camera::camera2pixel ( const Vector3d& p_c ){
    return Vector2d (
               fx_ * p_c ( 0,0 ) / p_c ( 2,0 ) + cx_,
               fy_ * p_c ( 1,0 ) / p_c ( 2,0 ) + cy_
           );
}

注意这里隐含了相机到相机归一化平面的过程p_c ( 0,0 ) / p_c ( 2,0 )和p_c ( 1,0 ) / p_c ( 2,0 )
先把像机坐标系下的点转化到归一化平面
$P_c$ = $\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ Z^{\prime }\end{array}\right]$

归一化之后

$\left[\begin{array}{c}\frac{X^{\prime }}{Z^{\prime }}\\ \frac{Y^{\prime }}{Z^{\prime }}\\ \frac{Z^{\prime }}{Z^{\prime }}\end{array}\right]$


归一化后转换成像素坐标(忽略畸变)

fx_ * p_c ( 0,0 ) / p_c ( 2,0 ) + cx_,
fy_ * p_c ( 1,0 ) / p_c ( 2,0 ) + cy_

$u$ = $f_x\ast \frac{X^{\prime }}{Z^{\prime }}+c_x$
$v$ = $f_y\ast \frac{Y^{\prime }}{Z^{\prime }}+c_y$

pixel2camera像素坐标转化为像机坐标系下面的点

Vector3d Camera::pixel2camera ( const Vector2d& p_p, double depth )
{
    return Vector3d (
               ( p_p ( 0,0 )-cx_ ) *depth/fx_,
               ( p_p ( 1,0 )-cy_ ) *depth/fy_,
               depth
           );
}

实际上有一个中间过程，就是先转化为归一化平面的点
这里的depth就是归一化的$\frac{X^{\prime }}{Z^{\prime }}$ $\frac{Y^{\prime }}{Z^{\prime }}$

$\frac{u-c_x}{f_x}$ = $\frac{X^{\prime }}{Z^{\prime }}$

$\frac{v-c_y}{f_y}$ = $\frac{Y^{\prime }}{Z^{\prime }}$

$\left[\begin{array}{c}\frac{u-c_x}{f_x}\\ \frac{v-c_y}{f_y}\\ 1\end{array}\right]$ = $\left[\begin{array}{c}\frac{X^{\prime }}{Z^{\prime }}\\ \frac{Y^{\prime }}{Z^{\prime }}\\ \frac{Z^{\prime }}{Z^{\prime }}\end{array}\right]$

world2pixel世界坐标转化为像素坐标

Vector2d Camera::world2pixel ( const Vector3d& p_w, const SE3& T_c_w )
{
    return camera2pixel ( world2camera(p_w, T_c_w) );
}

$X\ast f_x+c_x$ = $u$
$Y\ast f_y+c_y$ = $v$

pixel2world相素坐标转化为世界坐标

Vector3d Camera::pixel2world ( const Vector2d& p_p, const SE3& T_c_w, double depth )
{
    return camera2world ( pixel2camera ( p_p, depth ), T_c_w );
}

$\frac{u-c_x}{f_x}$ = $X$
$\frac{v-c_y}{f_y}$ = $Y$

上面是针孔模型可以对比看看鱼眼EUCM模型

6自由度 如何理解需要6个坐标才能确定一个刚体的位置？

首先，在三维空间中，对于一个质点有三个自由度，需要三个坐标来确定它的位置，这一点应该无可争议。而对于一个刚体，它在三维方向有几何尺度，那么我们需要知道它的摆放方式，这种摆放方式的确定需要另外三个坐标。而为什么是三个坐标呢，因为我们需要三个夹角，刚体中的任意一条线与xyz轴的夹角，就是这三个坐标。

如何理解其次坐标用途？

如何理解相机外参数矩阵单应性矩阵H本征矩阵E基础矩阵F？

1.相机外参数矩阵。告诉你现实世界点(世界坐标)是怎样经过旋转和平移，然后落到另一个现实世界点(摄像机坐标)上。

2.相机内参数矩阵。内参数矩阵M：将空间三维点投影到像平面上的二维点（注意顺序关系）的矩阵。

3.单应性矩阵H：一个平面上的点到另一个平面上的点的投影映射矩阵。多视场中会用到。

4.本征矩阵E:（以双目视觉为例）将真实世界中的点P在左摄像机观测到的（左摄像机坐标系的）三维坐标Pl与右摄像机观测到的点P的（右摄像机坐标系中的）三维坐标Pl关联起来的矩阵。

5.基础矩阵F：（以双目视觉为例）将点P投影到左摄像机图像坐标系中的二维坐标和右摄像机图像坐标系中的二维坐标点关联起来的矩阵。

如何理解等距变换、相似变换、仿射变换和射影变换？

等距变换就是对图像的旋转+平移 —图像相对原图大小不变。
相似变换对图像的旋转+平移+缩放 —图像相对原图变小了一些。
仿射变换就是对图像的旋转+平移+缩放+切变（shear），相比前两种变换图像的形状发生了改变，但是原图中的平行线仍然保持平行。
射影变换就是对图像的旋转+平移+缩放+切变+射影，相比前三种变换图像的形变更为自由，原图中的平行线经过变换之后已经不在平行，而可能相交于一点，射影变换就是把理想点（平行直线在无穷远处相交）变换到图像上。应用示例是相机成像原理。