你还不会栈和队列吗？（五千字超详解教程）

大家好呀我是小生今天我们来学习数据结构的栈和队列，小生为了方便大家理解特意附上了许多图片和源码一起加油吧 

下面是我们今天要学习的内容

 一.栈

         1.栈的基本概念

​2.栈的结构选择

顺序表和链表的优缺点对比：

用数组实现栈

用单链表实现栈

用带头双向循环链表实现栈

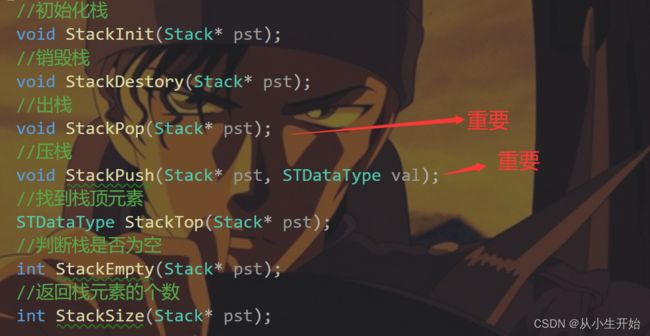
3.栈的常见接口的实现

栈的接口预览

​ 栈的构成

 栈的初始化

栈的销毁

压栈操作

出栈操作

取栈顶元素

判断栈是否为空

查找栈元素的个数

二.队列

1.队列的基本概念

2.队列的基本操作

队列的基本接口

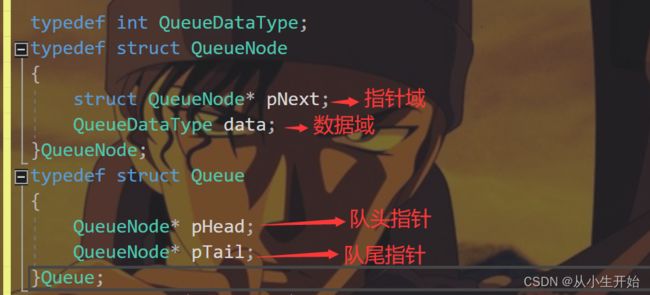
队列的组成

​队列的初始化

队列的销毁

入队

出队

寻找队头元素

寻找队尾元素

判断队列是否为空

求队列容量

三.小生想说的话

---

一.栈

1.栈的基本概念

栈是一种线性表，只允许在固定的一端进行插入和删除操作。进行数据插入删除的为栈顶，另一端为栈底。符合先进后出。既有数组栈和链式栈。

压栈：压栈就是栈的插入，也称之为入栈。

出栈：出栈就是栈的删除操作。

2.栈的结构选择

栈如何实现？是使用数组还是链表呢，在选择之前我们先了解一下顺序表与链表的优缺点:

顺序表和链表的优缺点对比：

顺序表的优点： 

1.可以按下标进行随机访问

2.顺序表的CPU高速缓存命中率比较高。

顺序表的缺点：

1.空间不够需要扩容，会存在一定的空间浪费。

2.当头部或者中间插入删除数据，需要挪动数据，效率较低。

链表的优点:

1.按需申请内存，不存在性能消耗，不存在空间浪费。

2.实现任意位置以O(1)的时间复杂度插入或者删除数据。

链表的缺点：

1.不支持下标的随机访问

2.顺序表的CPU高速缓存命中率比较高。

用数组实现栈

我们先来讨论一下数组，我们知道，我们永远是对栈顶进行操作，因此我们如果使用数组结构的话，应该将下标为0处设为栈底，将数组的末端设为栈顶。因为如果我们将下标为0的地方设为栈顶的话每次进行入栈或者出栈操作，后面的元素必须向前挪动，从而导致复杂度过大。小生画个图大家看看，方便大家理解：

---

用单链表实现栈

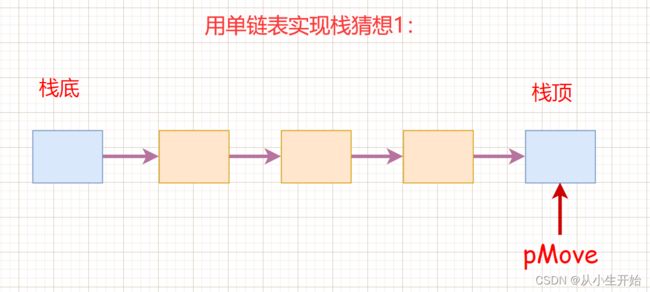
既然我们可以用数组实现栈，那么小生想问一个问题我们可以选择单链表吗？我们仔细想想，同样的道理，我们先来看看第一种方法:

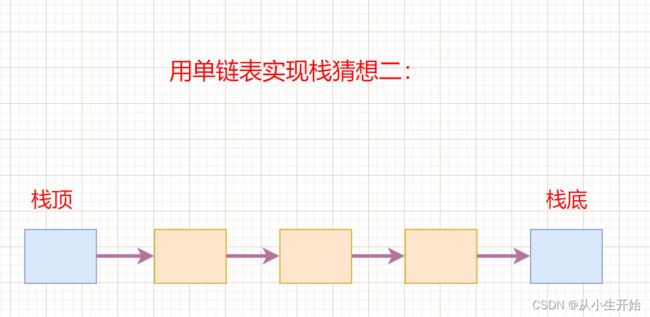
当我们用单链表将栈顶和栈底置为如上位置，我们发现入栈的时候，每次都需要用一个指针从头遍历整个链表找到尾结点，时间复杂度为O(n)，因此这样会非常麻烦，为了优化我们的程序，可以使用一个pMove指针存放尾部结点的地址，但是这样真的能够从根本上解决问题吗？入栈的问题解决了，但是小生想说的是如果出栈怎么办？难道用两个指针一个存放尾结点的地址另一个指针存放倒数第二个结点的地址吗？如果我要多次出栈呢？哈哈想想看，是不是很难解决实际的问题，但是这种思考方式让我们联想到了带头的循环链表，我们后面再谈。那么单链表真的不能实现吗？我们来看看下面这种方式：

或许你惊呆了，这两种猜想乍一看没什么区别，其实区别大了，猜想1在入栈和出栈的时候对链表进行的是尾插和尾删，我们可以知道，单链表每次尾插和尾删在很多时候都需要用pMove指针找尾结点，将该链表遍历一次，时间复杂度很大为O(n)，但是第二种猜想我们用的是头插和头删，时间复杂度为O(1)，因此第二种猜想明显符合我们栈的要求，非常便捷。 

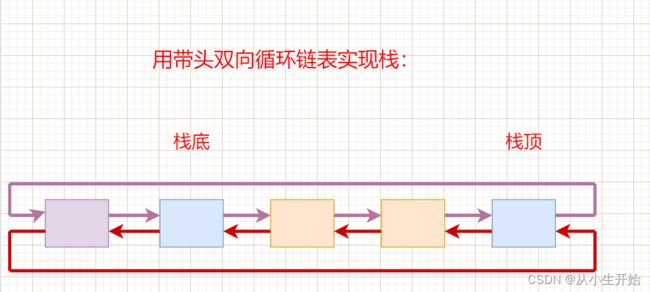
用带头双向循环链表实现栈

通过以上的分析我们可以得出三种实现栈的方式，那么们如何选择，我们选择数组，因为它往CPU高速缓存命中率更加高。因此能用数组就不选择链表。那我们接下来便用数组实现栈

3.栈的常见接口的实现

为了让大家看得更清楚，小生特意做成了图片和源码

栈的接口预览

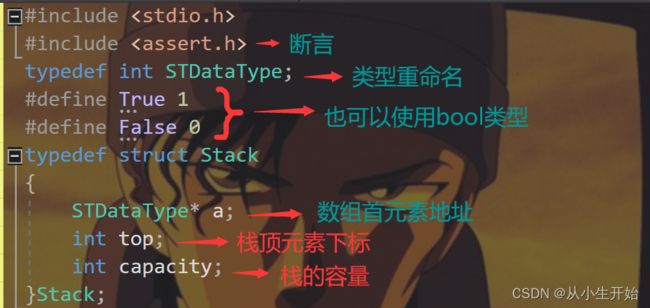
 栈的构成

我们知道，数组栈首先需要的就是一个记录栈顶元素的下标还需要一个容量以便顺序表已满后扩容。

 栈的初始化

这里小生提供两种初始化方式，可以直接初始化时不给数组空间，也可以初始化是该数组一定的空间，为什么要有第二种初始化方式呢？通过第二种初始化方法我们就可以让realloc直接实现二倍扩容，如果按照第一种初始化方式capacity扩大为原来的两倍后依然为0废话不多说，我们先来看看不给空间的初始化

void StackInit(Stack* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->capacity = 0;
	pst->top = 0;
}

看完了第一种，那让我们再来看看在初始化栈的时候给数组空间的情况：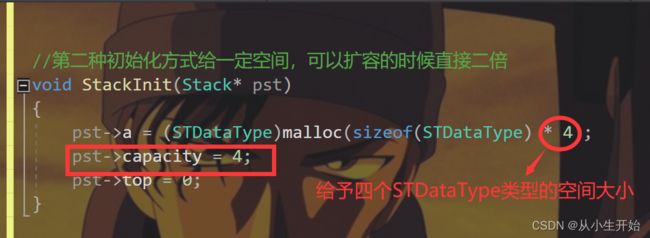

void StackInit(Stack* pst)
{
	pst->a = (STDataType)malloc(sizeof(STDataType) * 4);
	pst->capacity = 4;
	pst->top = 0;
}

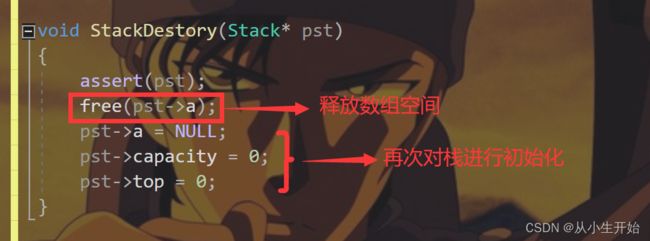
栈的销毁

void StackDestory(Stack* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->capacity = 0;
	pst->top = 0;
}

压栈操作

void Stackpush(Stack* pst, STDataType val)
{
	assert(pst);
	if (pst->top == pst->capacity)
	{
		STDataType* tmp = (STDataType)realloc(pst->a,sizeof(STDataType) * pst->capacity * 2);
		if (tmp == NULL)
		{
			printf("扩容失败!\n");
			exit(-1);
		}
		pst->a = tmp;
		pst->capacity *= 2;
	}
	pst->a[pst->top++] = val;
}

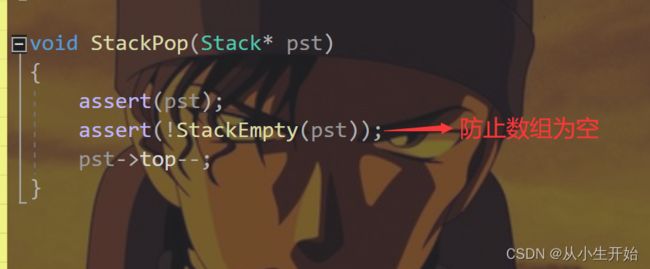
出栈操作

void StackPop(Stack* pst)
{
	assert(pst);
	assert(!StackEmpty(pst));
	pst->top--;
}

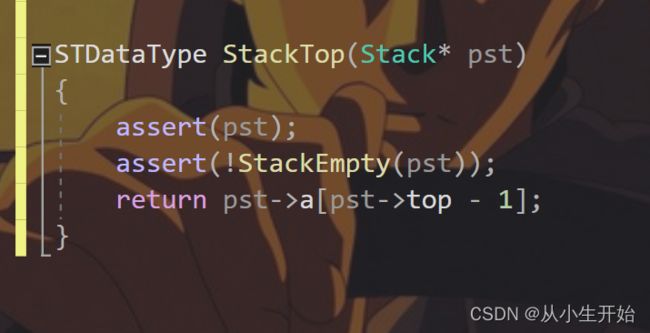
取栈顶元素

STDataType StackTop(Stack* pst)
{
	assert(pst);
	assert(!StackEmpty(pst));
	return pst->a[pst->top - 1];
}

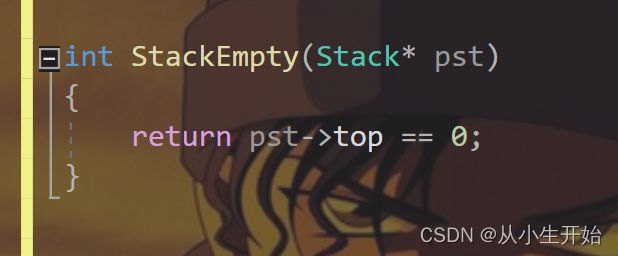
判断栈是否为空

int StackEmpty(Stack* pst)
{
	return pst->top == 0;
}

查找栈元素的个数

int StackSize(Stack* pst)
{
	assert(pst);
	return pst->top;
}

栈到这里它的基本操作就已经完结啦，小生觉得在图片上注释比文字的方式应该更加通俗易懂，大神们，接下来我们就要进入队列的学习啦，加油技术人！！！

二.队列

1.队列的基本概念

队列只允许在一端进行插入数据操作，在另一端进行删除操作。符合先进先出的原则。

队尾：进行插入操作的地方。

队头：进行删除操作的地方。

我们先通过一个图来认识一下队列的入队和出队操作

2.队列的基本操作

队列的基本接口

队列的组成

队列的初始化

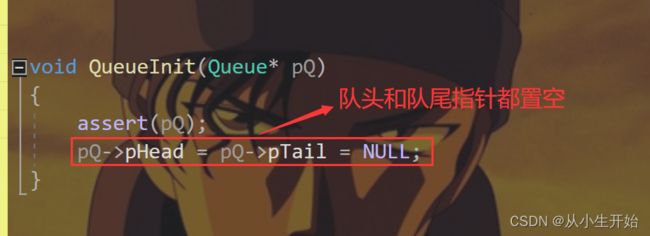
void QueueInit(Queue* pQ)
{
	assert(pQ);
	pQ->pHead = pQ->pTail = NULL;
}

队列的销毁

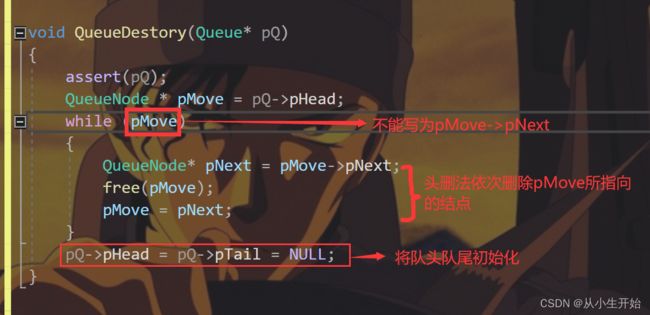
void QueueDestory(Queue* pQ)
{
	assert(pQ);
	QueueNode * pMove = pQ->pHead;
	while (pMove)
	{
		QueueNode* pNext = pMove->pNext;
		free(pMove);
		pMove = pNext;
	}
	pQ->pHead = pQ->pTail = NULL;
}

入队

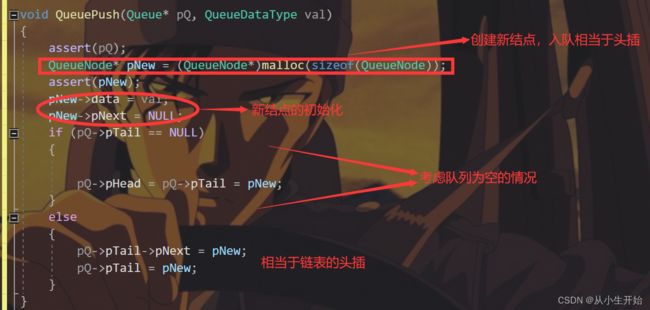
void QueuePush(Queue* pQ, QueueDataType val)
{
	assert(pQ);
	QueueNode* pNew = (QueueNode*)malloc(sizeof(QueueNode));
	assert(pNew);
	pNew->data = val;
	pNew->pNext = NULL;
	if (pQ->pTail == NULL)
	{
			
		pQ->pHead = pQ->pTail = pNew;
	}
	else
	{
		pQ->pTail->pNext = pNew;
		pQ->pTail = pNew;
	}
}

出队

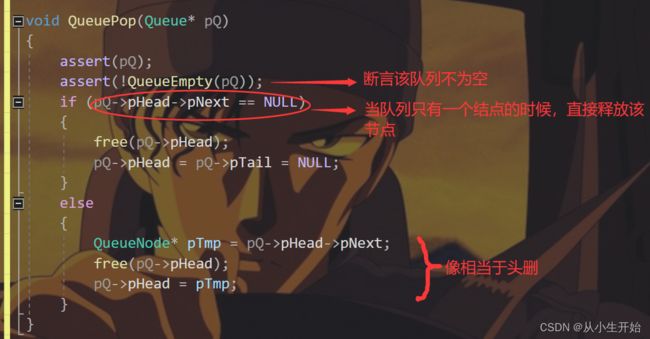
void QueuePop(Queue* pQ)
{
	assert(pQ);
	assert(!QueueEmpty(pQ));
	if (pQ->pHead->pNext == NULL)
	{
		free(pQ->pHead);
		pQ->pHead = pQ->pTail = NULL;
	}
	else
	{
		QueueNode* pTmp = pQ->pHead->pNext;
		free(pQ->pHead);
		pQ->pHead = pTmp;
	}
}

寻找队头元素

找队头元素和找队尾元素是最简单了啦，小生就不罗嗦了，直接上代码

QueueDataType QueueFront(Queue* pQ)
{
	assert(pQ);
	assert(!QueueEmpty(pQ));
	return pQ->pHead->data;
}

寻找队尾元素

QueueDataType QueueBack(Queue* pQ)
{
	assert(pQ);
	assert(!QueueEmpty(pQ));
	return pQ->pTail->data;
}

判断队列是否为空

bool QueueEmpty(Queue* pQ)
{
	assert(pQ);
	return pQ->pHead == NULL;
}

求队列容量

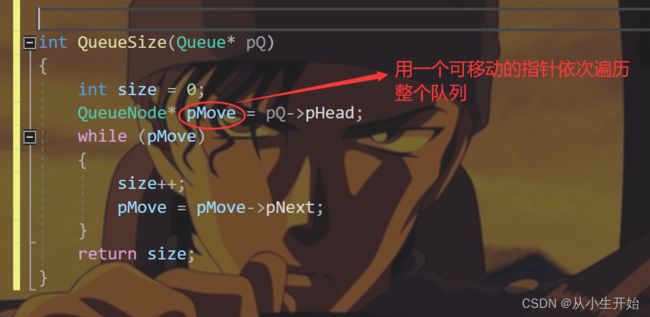
int QueueSize(Queue* pQ)
{
	int size = 0;
	QueueNode* pMove = pQ->pHead;
	while (pMove)
	{
		size++;
		pMove = pMove->pNext;
	}
	return size;
}

三.小生想说的话

当你看到这里的时候，咱们数据结构的栈和队列的基本操作你已经学完啦但是这其实只是数据结构的冰山一角罢了，小生后续会不断更新数据结构的基础与拓展。如果大神们觉得有帮助的话别忘了三连哦，加油，技术人！！！