【蓝桥杯Python组】2022年第十三届蓝桥杯省赛B组Python解题思路详解

第十三届蓝桥杯省赛B组Python解题思路详解

因为今年采用线上的举办方式进行比赛，所以组委会对题目做了一定的调整，将原来的5道填空+5道编程题变成了2道填空+8道编程题，据说是为了防止抄袭。其实题目的调整是一个方面，更重要的是题目难度也生了不少，有几个题目都是要通过数论中的公理或定理来进行推导的。我在考试过程中也仅仅做了ABCDGHJ这七道题，剩下的题目不是选择性跳过的，就是考虑了很久却也没有思路的。比赛结束后我请教了打ACM的段哥和秉哥，也重新思考了一下几个问题，虽然没有落实到代码中，但是也明白了大致的解题思路，接下来我将会这篇博客中大体写写自己的浅显理解。

QA：排列字母

这一题用Python还是比较方便的，总体思路是是将字符串转为列表，利用列表的内置快排+归并进行排序后再转回字符串，代码如下：

x=input()
x=list(x)
x.sort()
print(''.join(x))

QB: 寻找整数

答案就是蓝桥杯省赛日期：2022040920220409

这道题虽然位置靠前，但并不是可以暴力求解的，而是要使用数轮中中国剩余定理将问题进行转化求解。

线性同余方程组

中国剩余定理

物不知数问题：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

化解为线性方程组来表示即为

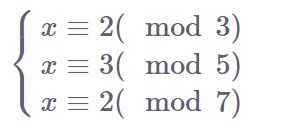
对于这个方程组我们可以对于每个方程构造一个数使得其模其它模数为0，模自己的模数为答案。即对于上面的方程可以构造：

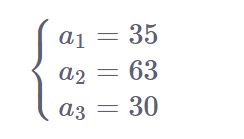
全部加起来即可得到一组特解，x0=128。得到通解x=x0+Mt（M为模数的最小公倍数，t属于全体整数），从而可以得到最小正整数解x=23。

所以这一问题我们可以直接套公式，用秉哥的话来说就是套板子。不过在这之前可以利用中国剩余定理的运算，将2-49的全体质数挑选出来作为模数m，找到对应的余数a，带入求解。具体代码如下：

import gmpy2

mod_num=[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]
rem_num=[1,2,4,4,0,10,0,18,15,16,27,22,1,11,5]

def crt(b,m):

    #乘积
    M = 1
    for i in range(len(m)):
        M *= m[i]
    #求M/mi
    Mm = []
    for i in range(len(m)):
        Mm.append(M // m[i])
    #求Mm[i]的乘法逆元
    Mm_ = []
    for i in range(len(m)):
        _,a,_ = gmpy2.gcdext(Mm[i],m[i])
        Mm_.append(int(a % m[i]))
    #求MiM'ibi的累加
    y = 0
    for i in range(len(m)):

        y += (Mm[i] * Mm_[i] * b[i])
    y = y % M
    return y

print(crt(rem_num,mod_num))

QC: 纸张尺寸

这道题也简单，就不赘述了

index=int(input()[-1])
h,w=1189,841
i=0
while i<index:
    h=int(h/2)
    h, w = max(h, w), min(h, w)
    i+=1
print(h)
print(w)

QD: 数位排序

总体思路：使用列表x存储1-n这n个数，将其对应元素的数位和存储到列表value中，依据value对x排序，使用zip对两个列表打包解包。代码如下：

n=int(input())
m=int(input())
x=[i for i in range(1,n+1)]
index=[]
for item in x:
    value = list(map(int, list(str(item))))
    index.append(sum(value))
result_list = [i for _,i in sorted(zip(index,x))]
print(result_list[m-1])

QE: 蜂巢

跳了跳了

QF: 消除游戏

总体思路：不能拘泥于细节，总览全体的排列模式。将边缘字符的重复模式分为奇重复和偶重复两个模式，偶重复一定可消除，奇重复可能会有剩余。消除一次判断一次边缘字符，直至没有边缘字符为止。

QG: 全排列的价值

题目中的全排列是烟雾弹，刚开始我也是尝试先使用回溯、递归之类的方法求全排列，再求其价值，但是对于2022这个规模的全排列，绝对绝对超时超内存，所以使用回溯算法能骗到的分十分有限，毕竟内存消耗太大。
这个题目应该是对应数论的某个定理的，我主要说一下自己的解题思路。
对于1 2 3这个列表，全排列及其得分如下

使用递推的方式来求这个价值。设n为1-n的全排列价值，leicheng(n)计算1-n的类乘积，leijia()计算1-n的累加和，则有：f[n]=leijia(n-1)·leicheng(n-1)+f[n-1]·n
简陋的推导过程

代码：

def leicheng(num):
    if num==1:
        return 1
    if num==2:
        return 2
    res=1
    for i in range(num,1,-1):
        res*=i
        res%=998244353
    return res

def leijia(num):
    res=0
    for i in range(num+1):
        res+=i
    return res%998244353

n=int(input())
ans=[0 for i in range(n+1)]
ans[1]=0
ans[2]=1
ans[3]=9

for i in range(4,n+1):
    ans[i]=(leijia(i-1)*leicheng(i-1)+ ans[i - 1]* i)%998244353
print(ans[n])

QH: 技能升级

每次选收益最大的来进行升级，升级完后进行衰减，衰减后再排序，总共升级M次。

import math


n, m = list(map(int, input().split()))
mp = {}
for i in range(0, n):
    Ai, Bi = list(map(int, input().split()))
    mp[i + 1] = [Ai, Bi, 0]
# print(mp)

temp = sorted(mp.items(), key=lambda mp: mp[1][0], reverse=True)
# print(temp)

res = 0
for i in range(0, m):
    index = temp[0][0]
    A = temp[0][1][0]
    B = temp[0][1][1]
    times = temp[0][1][2]
    # print(index,A,B,times)

    if times >= math.ceil(A / B):
        A = 0
        B = 0

    res += A
    A -= B
    times += 1
    mp[index] = [A, B, times]
    temp = sorted(mp.items(), key=lambda mp: mp[1][0], reverse=True)

print(res)

QI: 最长不下降子序列

QJ: 最优清零方案

代码：

n,k=list(map(int,input().split()))
a=list(map(int,input().split()))

index=0
sum_num=0
op=[-1 for i in range(k)]
while index<n-k+1:

    if 0 in a[index:index+k]:

        index+=1
    else:
        # print(index)
        for i in range(index,index+k):
            a[i]-=1
        sum_num+=1

print(sum(a)+sum_num)