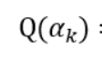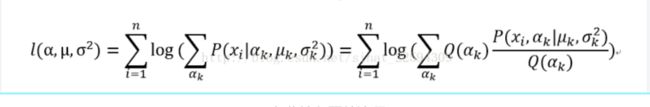学python和halcon哪个好学_一起学python-opencv二十五(opencv分水岭算法实践,GrabCut交互式前景提取)...
opencv分水岭实践
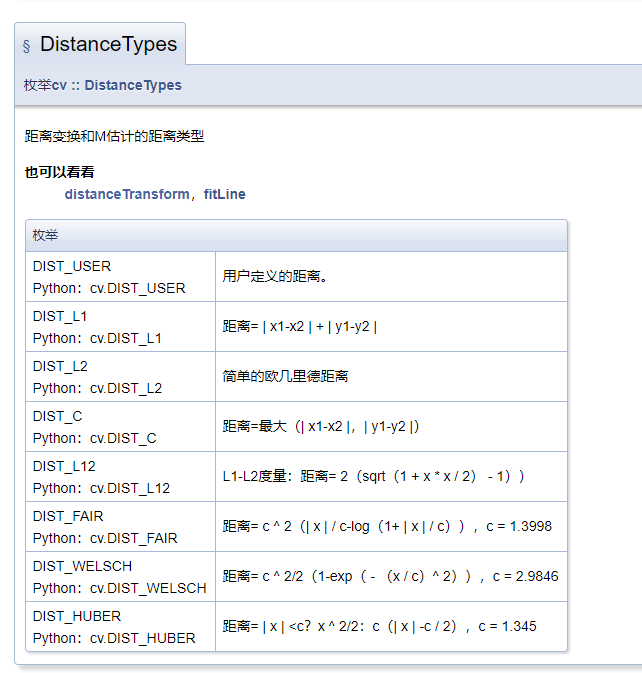
opencv有一个例子,这个例子是分割相互接触的物体。![]()
除去白点噪声,可以用开操作。如果里面有黑色的孔洞,可以用闭操作去除。上面的意思就是说因为结果是连着的,所以其实物体的边界是不太确定的。
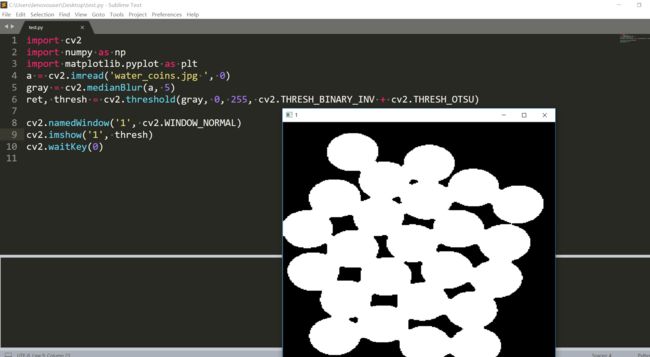
先用开操除去了一些噪点,其实iterations=1或者2结果都一样。这上面前景的获得是通过一个距离变换,然后二值化得到的。用到的函数是distanceTransform。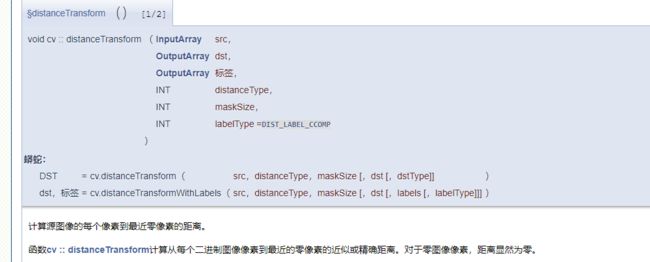
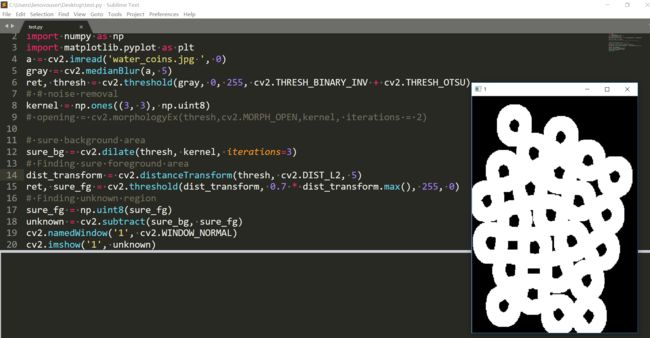
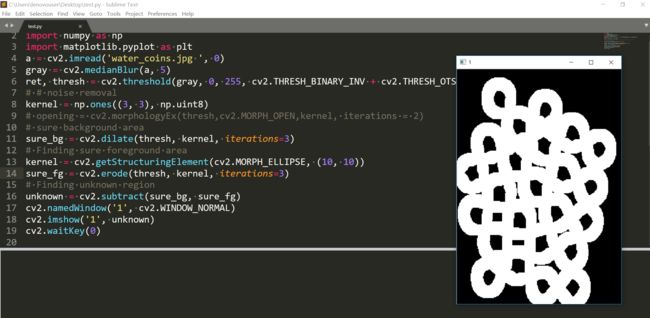
这里用距离变换只是为了得到硬币比较中心的位置而已,因为这些位置我们可以确定是单个硬币的区域,我觉得腐蚀完全可以完成这个功能,不过可能得多腐蚀几次或者用比较大的探针。
这个距离变换之后二值化的阈值也是随便选的而已,并没有什么太大的讲究,只要得到一个比较小的区域就可以。
这里得到位置区域的意思是,这些区域并不能分辨出来是属于哪一个硬币的或者是背景,所以是unknow。
这个函数可能就是用形态学操作提取出来的连通区域(上面简单说过这种方法)。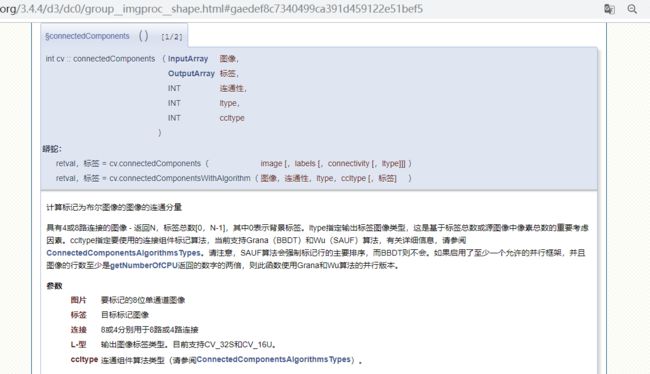
背景标签,背景应该就被认为是黑色的部分。可以选择4邻域或者8邻域的算法,并且算法也有很多。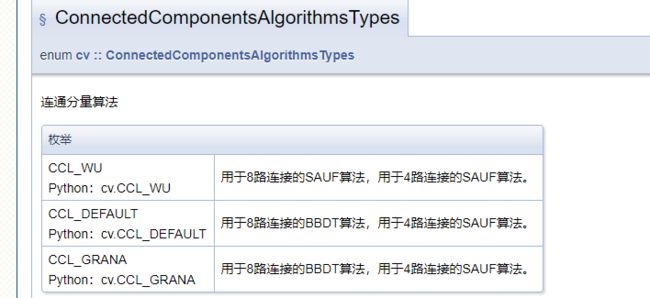
不过这个函数还有一种输入时不需要这个参数的,这个函数输出有retval和lables,等会试验一下都是什么。
但是如果背景被标记为0,那么分水岭算法会把它视作未知区域(前面介绍过),所以我们想要用一个不同的整数来标记它。我们把未知区域标记为0,而不是背景。markers=markers+1就是为了不让背景为1。
然后把unknow区域的都标记为0,在unknow图里面白色的是位置区域,所以是==255。
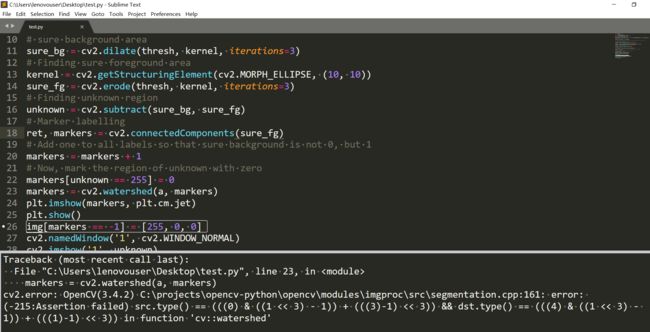
最后让输出的边界也就是值==-1的都化成红色,代表边界。
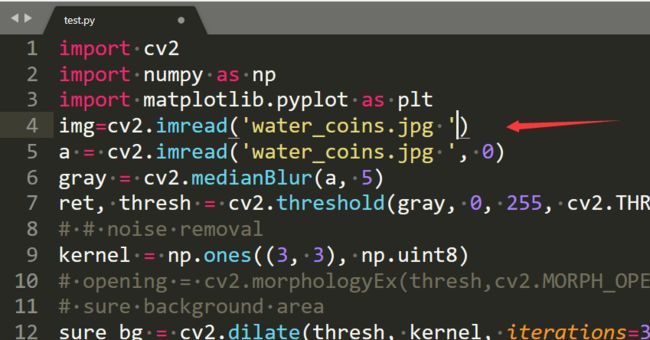
下面就来整体试验一下:
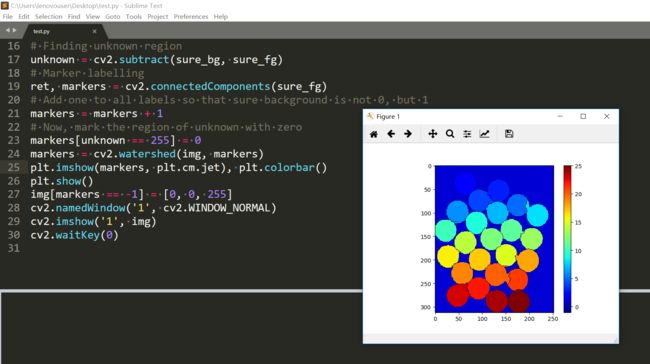
ret返回的是连通区域个数,而markers返回的是和原图像一样大小的标记矩阵。用plt中的jet的cmp格式显示。
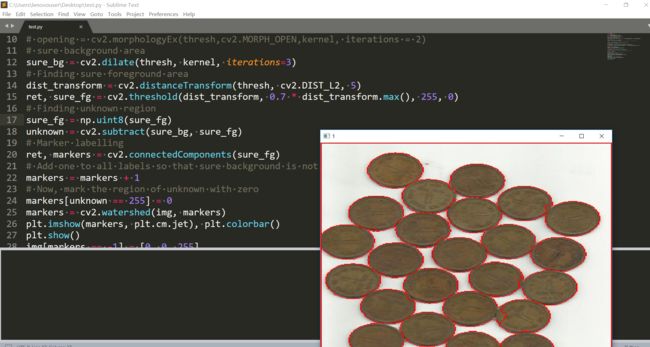
这个用的是腐蚀的结果,效果也不错,不同颜色代表不同的区域。输出的水坝位置用红色标注。
感觉也差不太多。这个例子我感觉其实不算好,因为其实没有太体现分水岭算法的原理。而且这个效果用霍夫圆检测能实现吧,我是这么想的。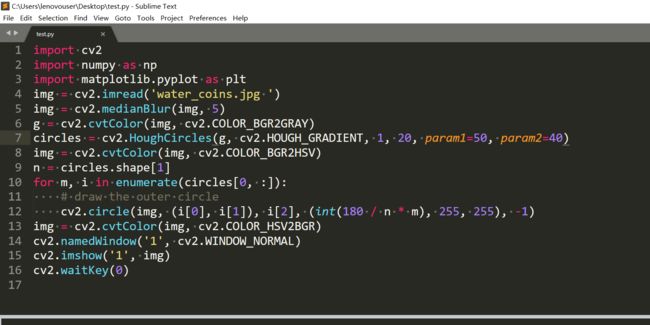
有两个圆没被识别出来,也许是我的一些参数调的不太好吧。
GrabCut前景提取
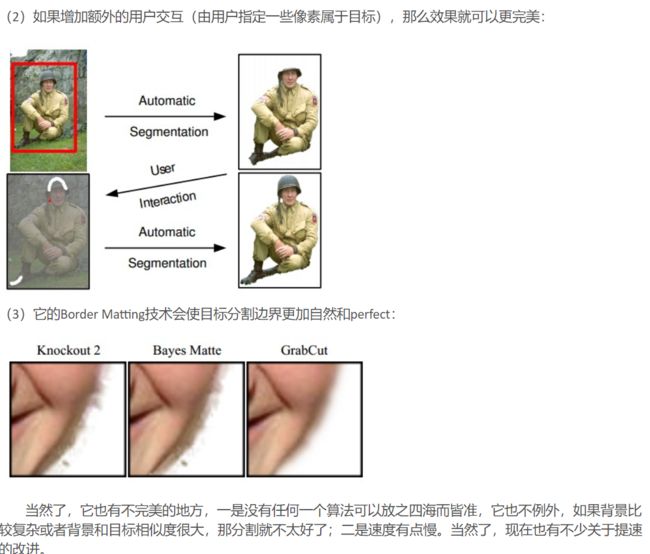
前景提取,说白了就是抠图,那这肯定是人来抠图就准确了,但是有的时候工作量很大,需要实现自动抠图,当然自动抠图可能效果不好,这个时候可能需要人工进行一些小的修正。
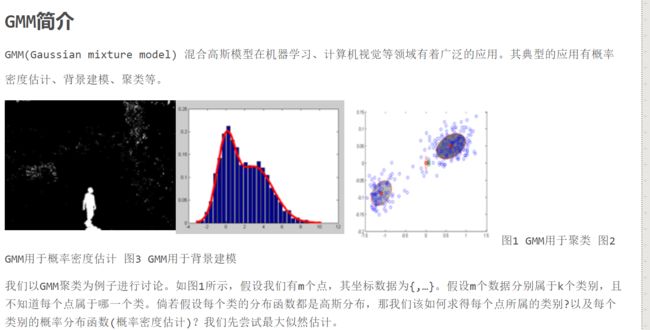
前景提取说白了也就是聚类,不过特征至少有空间位置,BGR通道的值,还有连通性等等一系列特征,根据这些特征把框内的像素点最终聚为两类,如果没有任何标签,就属于无监督学习,如果有一些标签,就属于半监督学习了。首先学习一下GMM。参考
https://www.cnblogs.com/zhangchaoyang/articles/2624882.html
https://www.cnblogs.com/insmod/p/3762206.html
这里属于的类别数和服从高斯分布都是假设的。为什么要假设高斯分布呢?https://blog.csdn.net/lpsl1882/article/details/78906274
这篇文章从熵的角度说明了为什么高斯分布这么常用。Maximum Likehood就是极大似然估计,这个大学概率论都有讲过。如果忘了,可以到https://blog.csdn.net/class_brick/article/details/79724660
https://blog.csdn.net/zengxiantao1994/article/details/72787849
一句话,极大似然估计就是在只有概率的情况下,忽略低概率事件直接将高概率事件认为是真实事件的思想。或者说利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值,也就是既然这个事件发生了,那么它就应该是最可能发生的,那么参数就应该朝着让它最可能发生的方向靠近。但其实这种思想并不符合大数定律。
根据样本数据,上式就是用极大似然估计得到的均值和方差,少了一个^,这个^代表估计得到的值。正规的写法应该这样。这个Σk更精确的应该叫做协方差矩阵。而这个x也可以是多维的,也就是可以是多维的高斯分布。![]()
这里找参数不是让6的期望最大,就是让6最大。参考https://blog.csdn.net/sinat_22594309/article/details/65629407
https://blog.csdn.net/livan1234/article/details/80871308
上过大学的人总不至于忘了jersen不等式了吧(琴生不等式)
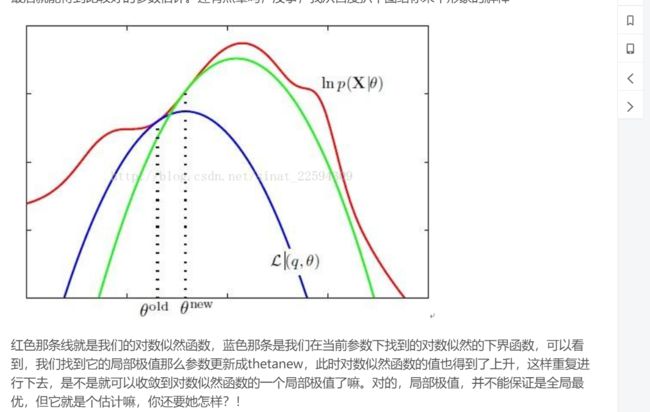
收敛一般的判定都是两次计算的结果小于某个数就可以。稍微详细一点:![]()
但是上面的ψ参数我感觉意义不明。下面的公式里面不应该出现w,权值就是ψ,不过后来想了想其实也没有错,因为这个式子变形过。
上面的ψ就是这里的α,是每一类占总体的比例。到此处我们已经了解了GMM,高斯分布可以是多维的,那个时候σ就是Σ(协方差)矩阵了。
下面参考https://blog.csdn.net/zouxy09/article/details/8532111
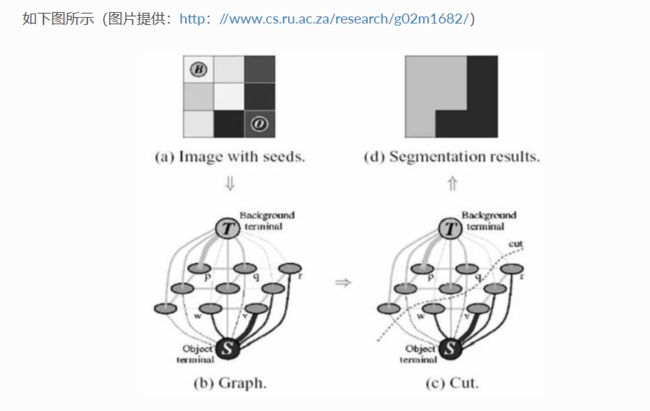
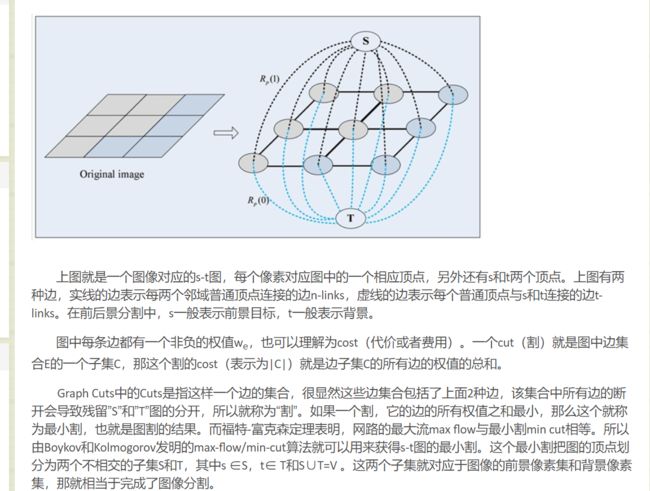
我们先来学习一下Graph Cut,这个顾名思义用到了图论的知识,图论我只在电路课上学过一点。
这个像素p属于某个标签的概率可以通过前面的GMM得出,这个应该要用二维的GMM了。
后来的修正其实就是在无监督学习中加入标签,可以说是半监督学习。
首先GMM的收敛性,在https://blog.csdn.net/livan1234/article/details/80871308里面证明了,(其实是证明了EM的收敛性),GMM是用了极大似然估计转化为了EM问题。
GrabCut原文链接(当然是英文的):http://dl.acm.org/citation.cfm?id=1015720
下载连接 http://delivery.acm.org/10.1145/1020000/1015720/p309-rother.pdf?ip=58.154.206.92&id=1015720&acc=ACTIVE%20SERVICE&key=BF85BBA5741FDC6E%2E4183B12E3311CD37%2E4D4702B0C3E38B35%2E4D4702B0C3E38B35&CFID=878051462&CFTOKEN=25926302&__acm__=1482114880_9a8e2ed4f77010d50d9987daa92e9715
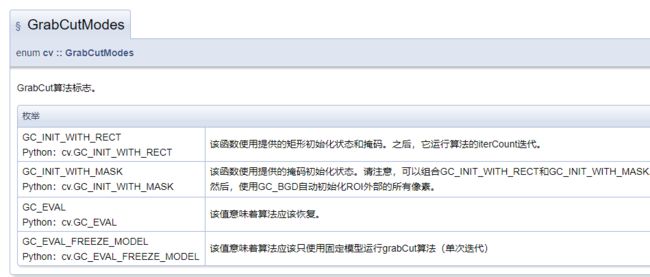
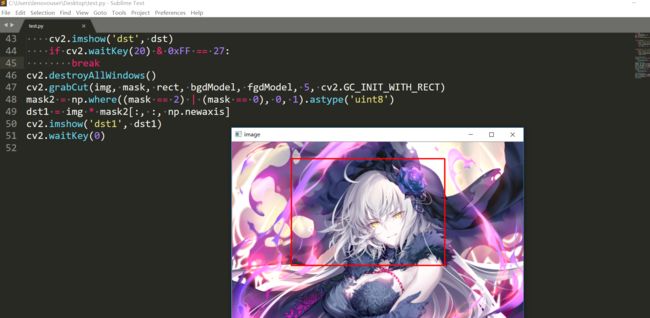
注意看喜爱按的mask,bgdModel和fgdModel都是InputOutArray,也就是既作为输入,又作为输出。
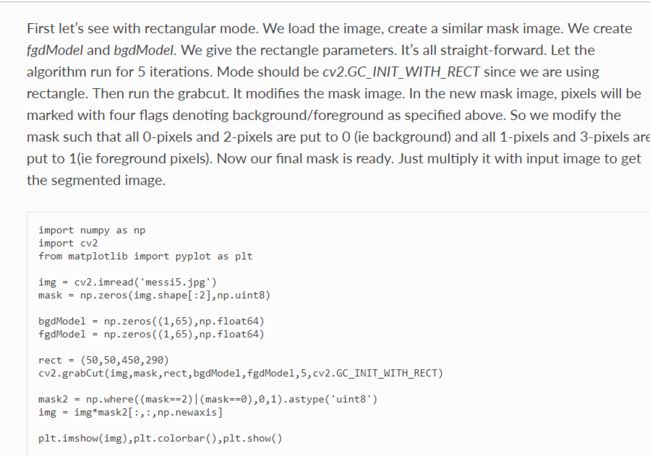
看官网的一个例子:
mask是和原来图像一样大小的单通道图像,它用来存储标签(0,1,2,3),
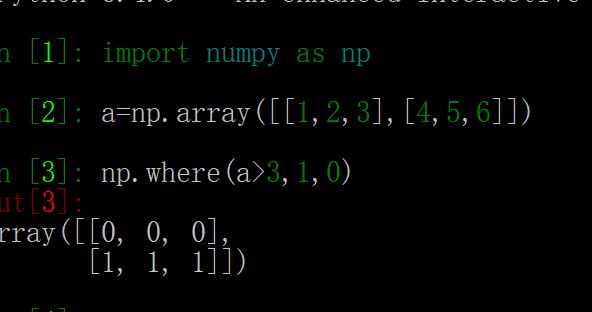
mask2 = np.where((mask==2)|(mask==0),0,1).astype('uint8')这一句是替换的。把2替换为0,3替换为1,np.where的这种用法以前也提到过,其实就是if mask[i,j]==2|0 mask[i,j]=0 else
关于最后的np.newaixs的理解:https://blog.csdn.net/molu_chase/article/details/78619731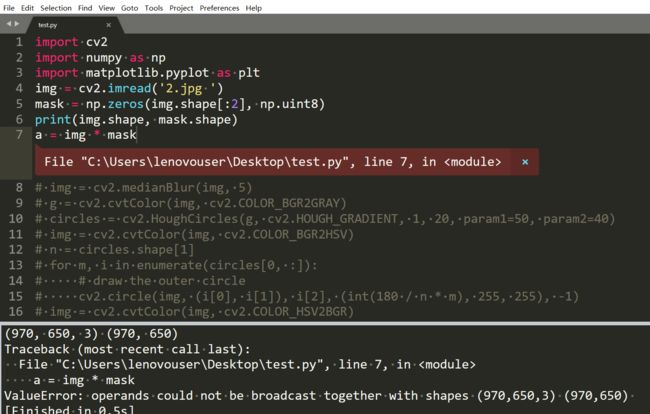
如果你还记得广播的知识,那么这样子是无法进行数组广播计算的。那么就得在mask的后面添1。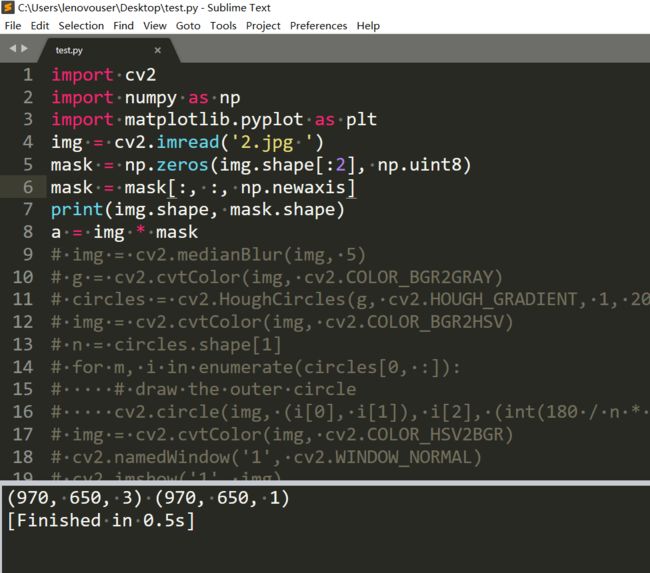
这个用reshape或者shape也能实现。因为背景是0,所以乘起来的结果也是0。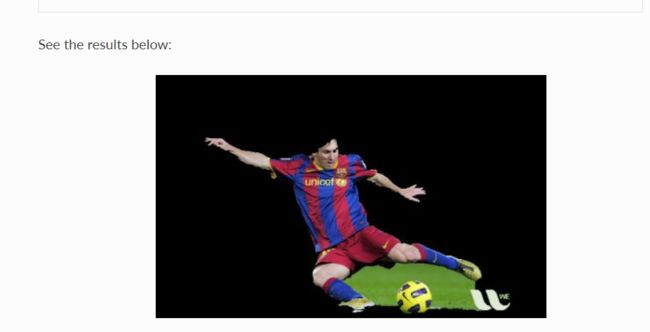
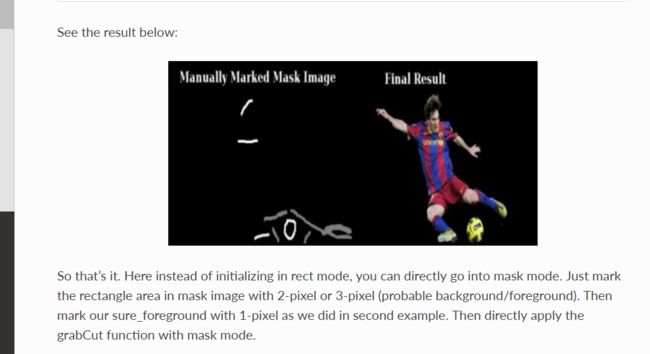
也就是我们人工修正的时候需要对掩模图像进行修正。我觉得我们可以和鼠标操作结合起来,让这个交互是可视的。
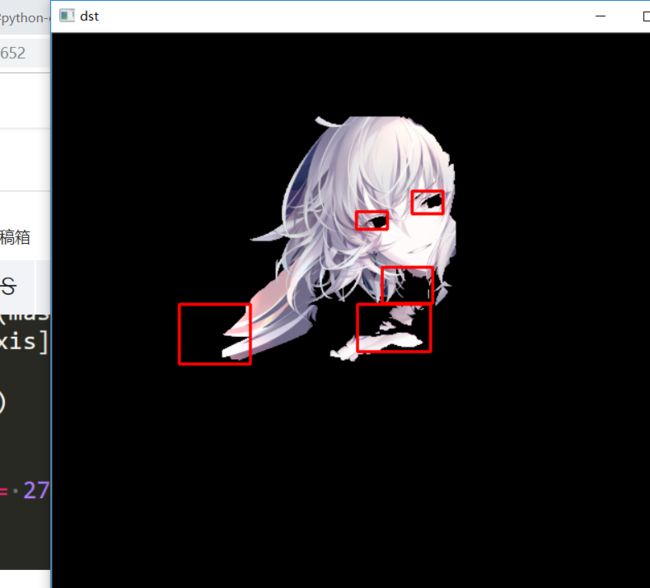
可以让画矩形框的操作不是手动输入而是用鼠标框选,还有修正的时候不是人工输入,而是鼠标框一个范围,让这个范围内的图像得到修正。下面是我写的一段代码: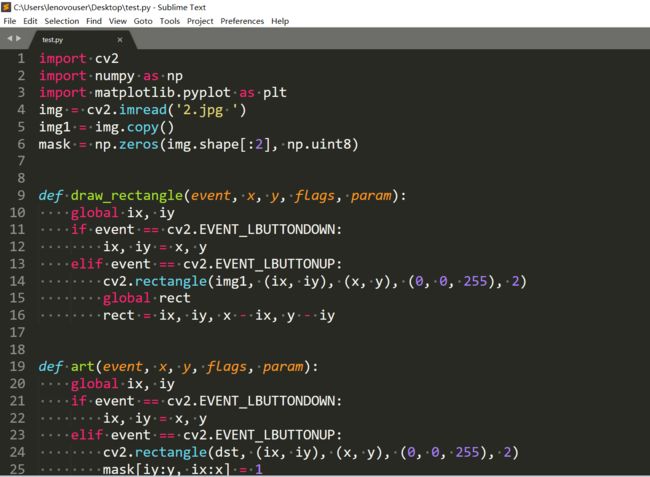
这个实现的就是可视化框选矩形和修正,具体代码请结合上面讲得理解,不再解释。
实现的功能就是:
这里修正的函数art其实可以更近一步,修正为前景的用鼠标左键框选,修正为背景的用鼠标右键框选。这个运算时候还是挺久的。