线段树原理及实现
文章目录
-
- 概念
- 原理
- 性质
- 作用
- 线段树基本操作
-
- 建树(build)
- 单点修改
- 区间修改
- 区间查询
概念
首先我们先明确两件事情!
1. 线段树他是个二叉搜索树! 2. 线段树是基于一个数组生成的!
线段树常用于统计区间上的信息:
其每个节点存储的是一个区间的信息,每个节点包含三个元素:
- 区间左端点
- 区间右端点
- 区间内维护的信息
原理
线段树的思想就是将数组内所有元素看作是一个区间,将每个区间递归的进行分解,直到区间内只剩下一个元素为止。
性质
- 线段树的每个节点都代表一个区间。
- 线段树的唯一根节点,代表整个 [ 1 , n ] {[1,n]} [1,n]区间。
- 线段树的每个叶节点,都代表长度为 1 {1} 1的区间 [ x , x ] {[x,x]} [x,x]。
- 对于每个内部节点 [ l , r ] {[l,r]} [l,r],它的左节点 [ l , m i d ] {[l,mid]} [l,mid],右节点 [ m i d + 1 , r ] {[mid + 1,r]} [mid+1,r],其中 m i d = ⌊ l + r 2 ⌋ {mid=⌊\frac{l + r}{2}⌋} mid=⌊2l+r⌋。
- 线段树除去最后一层,是一个满二叉树。
按照二叉树的标号对线段树进行编号,如下图:
根节点编号为 1 {1} 1,编号为 x {x} x的节点左节点为 x ∗ 2 {x*2} x∗2,右节点为 x ∗ 2 + 1 {x*2+1} x∗2+1。
可以发现树的最后一层节点在数组中存储,位置是不连续的。理想情况下: n {n} n个节点的满二叉树有 2 ∗ n − 1 {2*n-1} 2∗n−1个节点,但由于最后一层产生空余,为了要保证数组能存储整棵树,最后一层也要开到 2 ∗ n {2*n} 2∗n的空间。
因此一共需要开辟 4 n {4n} 4n的空间存储线段树。
作用
线段树将区间递归分为多个小区间,可以用来解决区间问题。
其最基本的作用有:
- 维护区间信息
- 合并区间信息
- 对序列进行维护,支持查询与修改操作
线段树基本操作
线段树的五个常用操作:
-
pushup:由子节点向上更新父节点的信息。 -
pushdown:把父节点的修改信息下传到子节点,也被称为懒标记(延迟标记)。这个操作比较复杂,一般不涉及到区间修改则不用写。 -
build:将一段区间初始化成线段树。 -
modify:修改操作。① 单点修改(需要使用pushup)。② 区间修改(需要使用pushdown)。 -
query:查询操作。① 单点查询。②区间查询
建树(build)
在建立线段树时,建树方式如下:
- 先开辟 4 n {4n} 4n大小的 t r {tr} tr数组空间
- 从根节点开始建立,根节点表示 [ 1 , n ] {[1,n]} [1,n]
- 递归的二分构建左子树 [ l , m i d ] {[l,mid]} [l,mid],右子树 [ m i d + 1 , r ] {[mid+1,r]} [mid+1,r]
- 向下递归到叶子节点结束,叶节点维护区间 [ x , x ] {[x,x]} [x,x],存储 a x {a_x} ax的值
- 回溯过程中,从下往上更新信息,即 v a l ( l , r ) = v a l ( l , m i d ) + v a l ( m i d + 1 , r ) {val(l,r)=val(l,mid)+val(mid+1,r)} val(l,r)=val(l,mid)+val(mid+1,r)
#define ls u<<1
#define rs u<<1|1
struct node{
int l, r;
ll sum;
}tr[N << 2];
int a[N];
void build(int u, int l, int r) {
tr[u] = {l, r};
if(l == r) { tr[u].sum = a[l]; return ;}
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
pushup(u);
}
建树操作时间复杂度: O ( n ) {O(n)} O(n)
单点修改
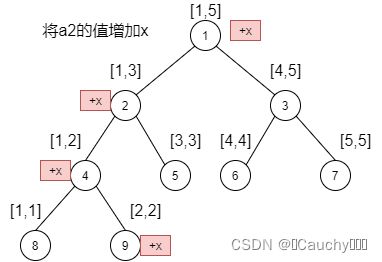
将 a i {a_i} ai的值增加 x {x} x,过程如下:
- 从根节点代表的区间 [ 1 , n ] {[1,n]} [1,n]出发,递归找到存储区间 [ i , i ] {[i,i]} [i,i]的叶节点。对 a [ i ] + = x {a[i]+=x} a[i]+=x
- 再从下往上更新存储区间 [ i , i ] {[i,i]} [i,i]的叶节点以及其到根节点路径上的所有区间信息
如图所示:
void modify(int u, int l, int r, int x) {
if (tr[u].l >= l && tr[u].r <= r) { tr[u].sum += x; return ; }
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(ls, l, r, x);
else modify(rs, l, r, x);
pushup(u);
}
main():
modify(1, x, x, y); // x,x就是对x单点进行修改
区间修改
线段树的区间修改也是将区间分成子区间,但是要加一个标记,称作懒标记。
懒标记的含义:
当前节点维护的信息已经根据标记更新过了,但当前节点之下的子节点仍需要更新。
举个例子: 给当前节点 u {u} u维护的区间 [ l , r ] {[l,r]} [l,r]的所有值加上 1 {1} 1,那么实际上并没有走到区间的所有叶子节点上,一个个的加上 1 {1} 1。而是给 u {u} u维护的懒标记 a d d {add} add加上 1 {1} 1,并更新 u {u} u维护的 s u m {sum} sum值。这样就做到了向下延迟修改,但是向上显示的是修改后的信息,所以查询能得到正确的结果。如果要查询 u {u} u下的子节点,那么需要将懒标记下传。
相对标记和绝对标记:
-
相对标记是将区间的所有数 + x {+x} +x 之类的操作,标记之间可以共存,跟打标记的顺序无关。- 所以可以在区间修改的时候不下推标记,留到查询的时候再下推。
- 注意:如果区间修改时不下推标记,那么
pushup中,必须考虑本节点的标记。
-
绝对标记是将区间的所有数变成 x {x} x 之类的操作,打标记的顺序直接影响结果,- 所以这种标记在区间修改的时候必须下推旧标记,不然会出错。
注意,有多个标记的时候,标记下推的顺序也很重要,错误的下推顺序可能会导致错误。
void modify(int u, int l, int r, int x) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].sum += len(u) * x;
tr[u].add += x;
return ;
}
pushdown(u); // 相对标记可以不在区间修改时下传
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(ls, l, r, x);
if(r > mid) modify(rs, l, r, x);
pushup(u);
}
举例说一下相对标记:
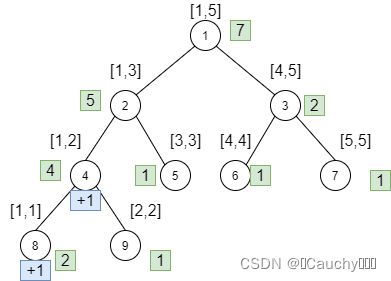
初始状态:4号节点有一个延迟标记 + 1 {+1} +1,所有叶子节点值全是1
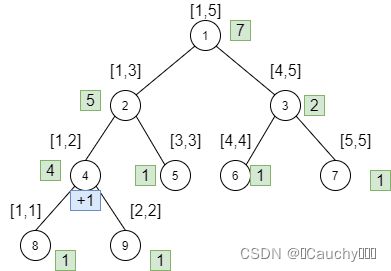
接下来,对 [ 1 , 1 ] {[1,1]} [1,1]区间修改 + 1 {+1} +1,modify执行到8号节点后:
由于我们采用的是相对标记,modify完8号点后,其实4号点的懒标记没下传给8、9两点,且8号点自己存在懒标记,值更新为2。
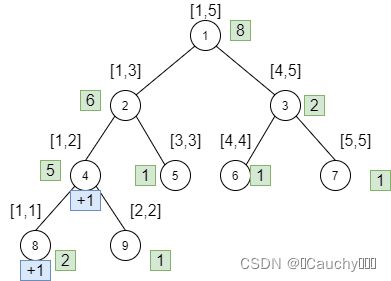
接下来进行回溯操作:
对于4号点,pushup函数中如果是原先采用绝对标记的写法:tr[u].sum = tr[ls].sum + tr[rs].sum;,那么显然会出错,因为到这回溯上去4号节点的值应该更新为4+1。所以我们需要考虑4号点自身的懒标记。
void pushup(int u) {
tr[u].sum = tr[u].add * len(u) + tr[ls].sum + tr[rs].sum;
}
待到询问 [ 1 , 1 ] {[1,1]} [1,1]区间,会在query中进行懒标记下传:
这样保证了结果无误。
区间查询
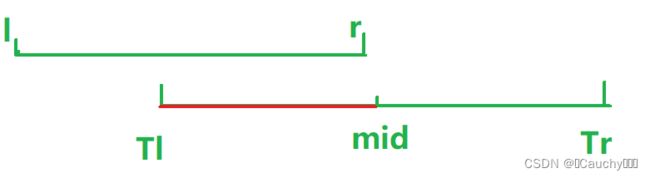
要查询在区间 [ l , r ] {[l,r]} [l,r]上的和,当前节点 u {u} u所表示的区间 [ T l , T r ] {[ T_l,T_r]} [Tl,Tr],则从根节点开始,递归时会遇到三种情况:
- [ T l , T r ] ⊂ {[ T_l,T_r]⊂} [Tl,Tr]⊂ [ l , r ] {[l,r]} [l,r],则立即回溯,该节点维护的 s u m {sum} sum值贡献给查询的答案。
- [ T l , T r ] ⊄ {[ T_l,T_r] ⊄} [Tl,Tr]⊄ [ l , r ] {[l,r]} [l,r] ,且 [ T l , T r ] ⋂ {[ T_l,T_r]⋂} [Tl,Tr]⋂ [ l , r ] ≠ ∅ {[l,r]≠ ∅} [l,r]=∅,与左侧有交集就递归左侧,与右侧有交集就递归右侧,都有交集就递归左右求解。
- [ T l , T r ] ⋂ {[ T_l,T_r]⋂} [Tl,Tr]⋂ [ l , r ] = ∅ {[l,r]=∅} [l,r]=∅ ,这种没交集的情况,直接不递归求解即可。
-
T L < = l < = T R < = r {T_L <= l <= T_R <= r} TL<=l<=TR<=r, 分两种情况:
- l > m i d {l > mid} l>mid,只递归 [ T L , T R ] {[T_L, T_R]} [TL,TR]右边。
- l < = m i d {l <= mid} l<=mid,递归 [ T L , T R ] {[T_L, T_R]} [TL,TR]左右两边,但右边递归一次下去,直接满足上述的第一种情况,直接返回。
- 对称的一种情况:
-
T L < = l < = r < = T R {T_L <= l <= r <= T_R} TL<=l<=r<=TR
- r < = m i d {r <= mid} r<=mid,只递归左边。
- l < = m i d {l <= mid} l<=mid,只递归右边。
- 否则,递归左右两边。
- 直观代码如下:
ll query(int u, int l, int r) {
// 1.被包含,直接返回
// Tl-----Tr
// L-------------R
if(tr[u].l >= l && tr[u].r <= r) { return tr[u].sum; }
int mid = tr[u].l + tr[u].r >> 1;
// pushdown(u); 有区间修改,懒标记,才需要
ll v = 0;
// 2. 左区间
// Tl----m----Tr
// L-------------R
if(l <= mid) v = query(ls, l, r);
// 3. 右区间
// Tl----m----Tr
// L---------R
if(r > mid) v += query(rs, l, r);
// Tl----m----Tr
// L-----R
//2.3涵盖了这种情况
return v;
}
示例:
该操作时间复杂度大约在: O ( 4 l o g ( n ) ) {O(4log(n))} O(4log(n))