机器学习的模型性能度量：评估指标PR对比ROC/AUC

  一般，对学习器的泛化性能进行评估，需要有能衡量模型泛化性能的评价标准，即性能度量（performance measure）。性能度量反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果，并通过这个指标来进一步调参逐步优化我们的模型。下面是一个机器学习小白的学习记录。

混淆矩阵

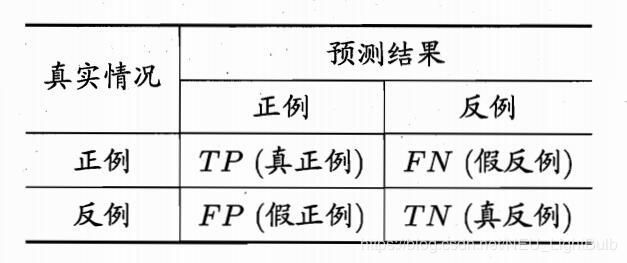
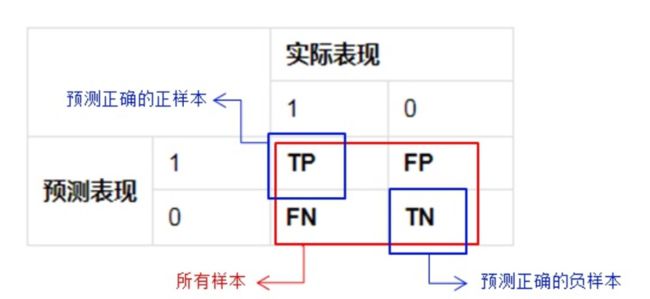
  对于二分类的模型，可以把预测情况与实际情况的所有结果两两组合，结果就会出现以下4种情况，就组成了分类结果的混淆矩阵（confusion matrix）：

  令TP、FP、TN、FN分别表示其对应的样例数，则显然有TP+FP+TN+FN=样例总数。分类的准确率可以表示为预测正确的结果占总样本的百分比，其公式如下：
$$准确率=\frac{TP+TN}{TP+TN+FP+FN}$$

  由于样本不平衡的问题，导致即使得到较高的准确率结果，并不能作为很好的指标来衡量结果。举个简单的例子，比如在一个总样本中，正样本占90%，负样本占10%，样本是严重不平衡的，对于这种情况，即使全部样本预测为正样本即可得到90%的高准确率。因此说明如果样本不平衡，准确率就会失效。

精准率和召回率

  精准率（Precision）又叫查准率，它是针对预测结果而言的，它的含义是在所有被预测为正的样本中实际为正的样本的概率。意思就是，在预测为正样本的结果中，我们有多少把握可以预测正确，其公式如下：
$$精准率=\frac{TP}{TP+FP}$$

  召回率（Recall）又叫查全率，它是针对实际样本而言的，它的含义是在实际为正的样本中被预测为正样本的概率，其公式如下：
$$召回率=\frac{TP}{TP+FN}$$

应用场景1：在信息检索中，查准率是“检索出的信息中有多少比例是用户感兴趣的”；查全率是“用户感兴趣的信息中有多少被检索出来了”。在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容是用户感兴趣的，因此查准率更为重要。

应用场景2：网贷违约率为例，若仅以精确率为度量标准，非常谨慎地进行正预测，那么只给收入最低、学历最低、工作没有保障的少量用户分类为正(Positive)，判断他们将无力偿还贷款，那精确度将非常高。但是如果我们把过多的将坏用户当成好用户导致召回率偏低，后续可能发生的违约金额会远超过好用户偿还的借贷利息金额，造成严重偿失。

应用场景3：流行病检验中，假设检疫局仅以召回率作为唯一度量标准进行分类，那么将以非常松散的标准进行正(Positive)分类，将大部分人预测为患病，自然这个方法就会使得隔离成本激增；但如果查准率较高，就是只将最有把握患病的人进行隔离，自然风险控制能力就很差（很大可能放走了携带病毒的人）。

  由上述描述可以看出，查准率和查全率是一对矛盾的度量，一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。在很多情形下，可根据学习器的预测结果对样例进行排序，比如逻辑回归的输出是一个0到1之间的概率数字，想要根据这个概率判断正负样本的话，就必须定义一个阈值。排在阈值之前的是学习器认为可能是正例的样本，排在后面的则是学习器认为不可能是正例的样本。可以将这些指标按条件概率表示：
$$\begin{gathered} 精准率=P（Y=1|X=1） \\ 召回率=P（X=1|Y=1） \end{gathered}$$

P-R曲线

  按上述学习器预测顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率，以查准率为纵轴、查全率为横轴作图，就得到了P-R曲线。

• 如何判断两个学习器的性能呢？若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者；如果两个学习器的P-R曲线发生了交叉，一般会选择比较P-R曲线下面积的大小，面积大的学习器在查准率和查全率会相对“双高”。
• 如何找到一个最合适的阈值满足我们的需求呢？通常我们希望查准率和查全率同时都非常高，但实际上这两个指标是一对矛盾体，如果想要找到二者之间的一个平衡点，可以是查准率和查全率相等时的取值（曲线与y=x的交点，在后面的ROC曲线上可以选择y=1-x的交点），一般需要结合具体场景去选择。

F-score

  在实际情况中，不会有分类器仅仅以精确度(Precision)或者召回率(Recall)作为单一的度量标准，而是使用这两者的调和平均，于是就有了F值(F-Score)，F值的一般表达式为：
$$F_{\beta }=(1+{\beta }^2)\times \frac{Precision\times Recall}{{\beta }^{2}Precision+Recall}$$
其中，$\beta$表达了对查准率/查全率的不同偏重，$\beta >1$表示分配给召回率(Recall)的权重更高，$\beta <1$表示分配给精确度(Precision)的权重更高。
  以上介绍的度量标准都是在已经做出分类的前提下，也就是说目标已经被成功分好类。实际上我们用特征值得出的是一个分类的概率，然后用某一个值将这个连续值切断，进行硬分类。所以，具体的类别实际上非常取决于这个阈值，假如选择的阈值很低，则被分成正类(Positive)的样本数会非常多；反之，如果选择的阈值很高，则被分类成负类(Negative)的样本数会比较多。

ROC/AUC

  ROC（Receiver Operating Characteristic，“受试者工作特征”），与P-R曲线相同的是，也是根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图；与P-R曲线不同的是，ROC曲线的纵轴是TPR（真正率），横轴是FPR（假正率）。

TPR：在所有实际为正的样本中，被正确地判断为正的比例。（与召回率的表达式相同）
$$TPR=\frac{TP}{TP+FN}$$
FPR：在所有实际为负的样本中，被错误地判断为正的比例。
$$FPR=\frac{FP}{FP+TN}$$

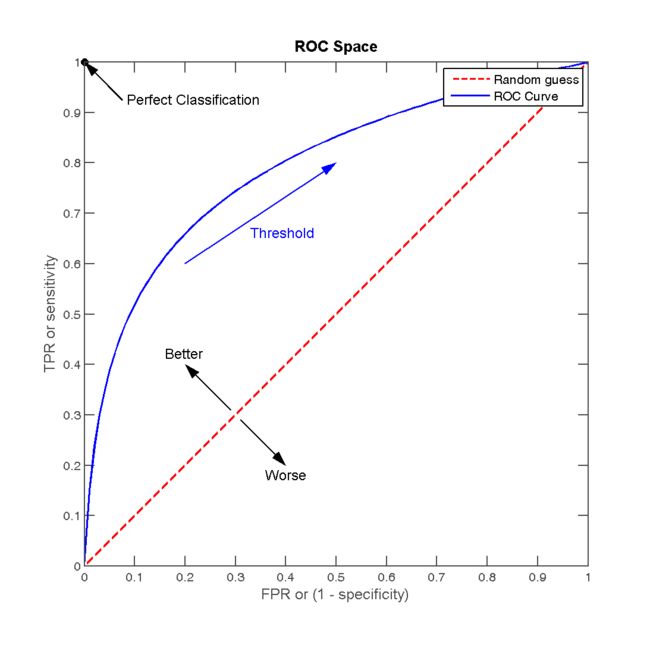
  根据上图，五角星代表正样本，圆代表负样本，不同的阈值作为分界线。当阈值低的时候，会有更多的样本被预测为正样本，所以TP、FP会更多，同时TN、FN更少，TPR、FPR都高；相反，当阈值高的时候，更少的样本被预测为正，TP、FP更少，TN、FN更多，TPR、FPR都低。ROC曲线便可反映出这种变化：

ROC曲线图中的四个特殊点：

• 第一个点：(0,1)，即FPR=0, TPR=1，这意味着FN=0，并且FP=0。即图中的左上角，这是完美的分类器，它将所有的样本都正确分类。
• 第二个点：(1,0)，即FPR=1，TPR=0，类似地分析可以发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案。
• 第三个点：(0,0)，即FPR=TPR=0，即FP=TP=0，可以发现该分类器预测所有的样本都为负样本（negative）。
• 第四个点：（1,1），分类器实际上预测所有的样本都为正样本。

  经过以上的分析，ROC曲线越接近左上角，该分类器的性能越好。也就是说，ROC 曲线下的面积越大，模型就越好，这个曲线下面积就称为 AUC（Area Under ROC Curve）。AUC介于0.5和1之间，AUC = 0.5时，模型没有预测价值，因为随机判断正负样本覆盖率应该都是50%。

KS(Kolmogorov-Smirnov)值

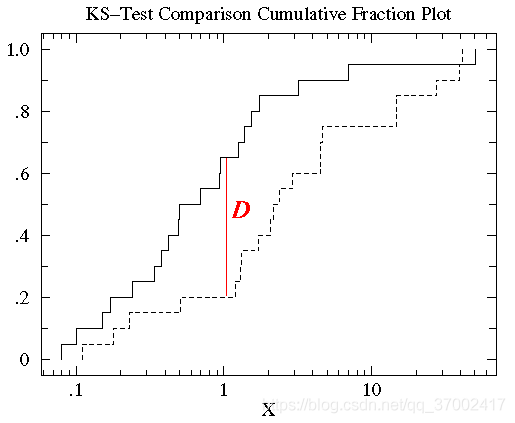
  KS=max(TPR-FPR)，即为TPR与FPR的差的最大值。KS值可以反映模型的最优区分效果，此时所取的阈值一般作为定义好坏用户的最优阈值。如下图所示，K-S曲线的横轴是数据预测结果的阈值，纵轴是累积概率TPR（上面那条）与FPR（下面那条）的值，值范围[0，1] 。两条曲线之间之间相距最远的地方（D）对应的阈值，就是最能划分模型的阈值。

AUC的一般判断标准	KS值的一般判断标准
0.5~0.7：效果较低，但用于预测股票已经很不错了	< 0 模型错误
0.7~0.85：效果一般	0~0.2 模型预测能力较差
0.85~0.95：效果很好	0.2~0.3 模型可用
0.95~1：效果非常好，但一般不太可能	> 0.3 模型预测性较好

  了解了这些指标定义后可以发现，对于分类模型，ROC曲线、AUC、KS是综合评价模型区分能力和排序能力的指标，而精确率、召回率和F1值是在确定最佳阈值之后计算得到的指标。

P-R曲线和ROC曲线的对比

  P-R曲线无法像ROC一样保证单调性。当需要获得更高recall时，需要输出更多的正样本，此时，precision会伴随出现下降/不变/升高的可能情况，得到的曲线会出现浮动差异（出现锯齿）。
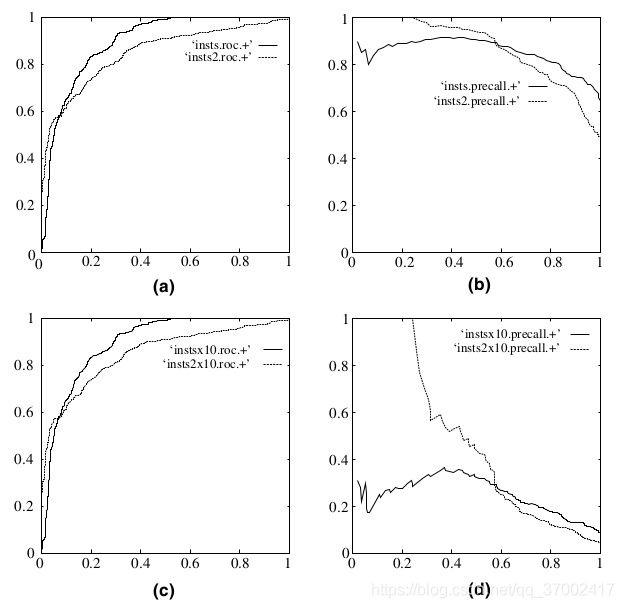
  ROC评估指标能降低不同测试集带来的干扰，更加客观的衡量模型本身的性能。也就是说，ROC曲线更能反映同一条件下不同模型的性能，也就是AUC值本身的意义没有相对大小的意义大。具体地，相比于P-R曲线，ROC曲线有一个巨大的优势就是，当正负样本的分布发生变化时，其形状能够基本保持不变，而P-R曲线的形状一般会发生剧烈的变化。如下图所示，（a）（c）为ROC曲线，正负样本比例1:1；（b）（d）为P-R曲线，正负样本比例为1:10。因此，在negative instances的数量远远大于positive instances的数据集里，P-R曲线更能有效衡量分类器的好坏。也就是说，当同一模型在不同数据集进行预测时，P-R曲线更能反映出当前模型的优劣，因为ROC对类分布不敏感，就容易造成一个看似比较高的AUC对应的分类效果实际上并不好。更进一步分析，因为P-R曲线看重整体的准确率，所以对于不平衡问题，看总体准确率的话，模型会被多数类“带走”，换句话说，就是会导致即使模型没有任何变化， 对模型的评价却会波动。然而，ROC曲线是分别在两个类里看准确率，所以不会被“带走”，会比较“照顾”少数类。所以，一般在假定正负样本均衡的时候多用ROC/AUC，而实际工程更多存在的数据标签倾斜问题使用F1。

参考链接：https://www.zhihu.com/question/30643044