用梯度下降算法解决回归问题(Python实现)
线性回归问题在数学上是一例很经典的问题,此类问题的解法无非两大类:1、最小二乘法;2、梯度下降算法,在此处,我们用梯度下降算法来解决一个最简单的线性回归问题。
1. 构建数据样本
我们这里用自己模拟生成的一段数据,一共200个样本,样本为一个二元一次方程,加上一个随机噪声:
y = wx + b + nos (我样本的 w 为1.8, b 为5 其中 nos 为随机噪声,取值范围为[-4,4])
这里我就不过多赘述了,直接上代码:
from __future__ import print_function
import time
import random
start = time.perf_counter()
#创建文件
fp = open("test.txt","w")
for i in range(10):
for numx in range(-10,10):
numb = random.uniform(-4, 4) + 5 #常数加上一个随机噪声
numy = 1.8*numx + numb
fp.write(str(numx) + ' ' + str(numy) + '\n')
fp.close()
end = time.perf_counter()
print("运行耗时:", end-start)
此处生成的 test.txt 即为我们所要用到的原始数据样本。
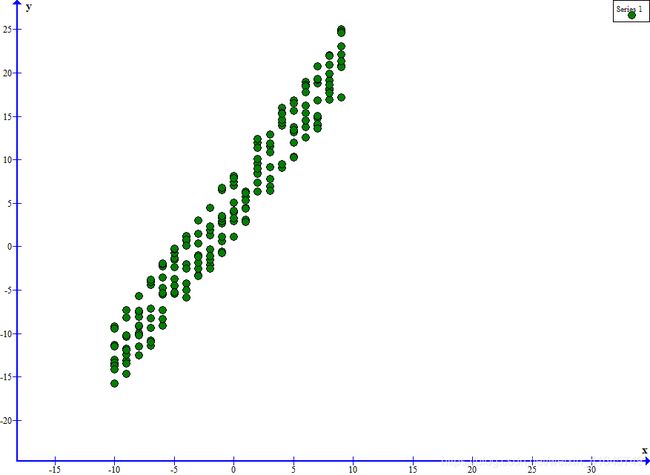
2. 开始用梯度下降算法来处理原始数据,求取拟合函数
具体数学推导过程我以后更新,今晚太晚了。。。。
直接上代码:
from __future__ import print_function
import torch
import time
import random
import numpy as np
start = time.perf_counter()
#获取所有点的总误差的均值
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (w * x + b)) ** 2
return totalError / float(len(points))
#梯度算法
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
#开始迭代
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iteration):
b = starting_b
w = starting_w
for i in range(num_iteration):
b, w = step_gradient(b, w, np.array(points), learning_rate)
return [b, w]
def run():
points = np.genfromtxt("test.txt", delimiter=" ")
learning_rate = 0.0005
initial_b = 0
initial_w = 0
num_iterations = 10000
print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
.format(initial_b, initial_w, compute_error_for_line_given_points(initial_b, initial_w, points)))
print("Runing")
[b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
print("After {0} iterations b = {1} w = {2}, error = {3}".
format(num_iterations, b, w, compute_error_for_line_given_points(b, w, points)))
if __name__ == '__main__':
run()
end = time.perf_counter()
print("运行耗时:", end-start)

我们可以直接看到运行出来的结果,迭代10000次求出来的 b = 5.076,w = 1.795,所以:
拟合结果为:y = 1.795 * x + 5.076
原始函数为:y = 1.8 * x + 5
我们从图上直观看出我们的拟合结果:
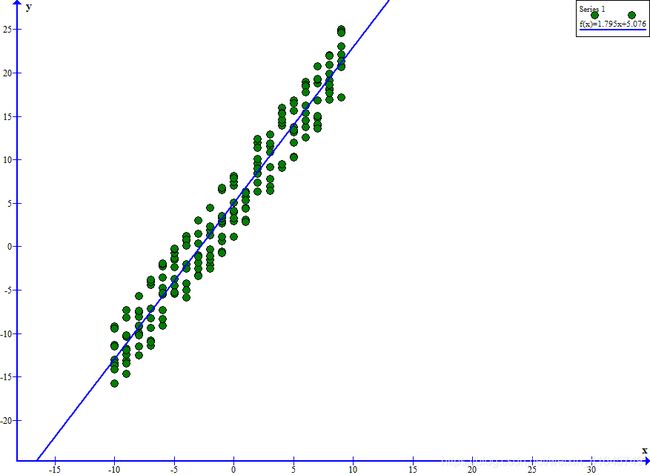
至此,我们可以更直观看出我们梯度下降算法所求出的函数的拟合效果还是很不错的,这就是我分享的梯度下降算法姐姐线性简单的线性回归问题。