知识蒸馏Knownledge Distillation

知识蒸馏源自Hinton et al.于2014年发表在NIPS的一篇文章：Distilling the Knowledge in a Neural Network。

1. 背景

一般情况下，我们在训练模型的时候使用了大量训练数据和计算资源来提取知识，但这不方便在工业中部署，原因有二：
（1）大模型推理速度慢
（2）对设备的资源要求高（大内存）
因此我们希望对训练好的模型进行压缩，在保证推理效果的前提下减小模型的体量，知识蒸馏(Knownledge Distillation)属于模型压缩的一种方法 [1]。

2. 知识蒸馏

名词解释：
cumbersome model：原始模型或者说大模型，但在后续的论文中一般称它为teacher model；
distilled model：蒸馏后的小模型，在后续的论文中一般称它为stududent model；
hard targets：像[1, 0, 0]这样的标签，也叫做ground-truth label；
soft targets：像[0.7, 0.2, 0.1]这样的标签；
transfer set：训练student model的数据

好模型的目标不是拟合训练数据，而是学习如何泛化到新的数据。所以蒸馏的目标是让student学习到teacher的泛化能力，理论上得到的结果会比单纯拟合训练数据的student要好 [3]。显然，soft target可以提供更大的信息熵，所以studetn model可以学习到更多的信息。

通俗的来讲，粗暴的使用one-hot编码把原本有帮助的类内variance和类间distance都忽略了，比如猫和狗的相似性要比猫与摩托车的相似性要多，狗的某些特征可能对识别猫也会有帮助（比如毛发），因此使用soft target可以恢复被one-hot编码丢弃的信息 [2]。

在Hinton et al. 发表的这篇论文中，作者提出了"softmax temperature"的概念，其公式为：
$$q_i=\frac{\exp (z_i/T)}{{\sum }_j^{}\exp (z_j/T)}$$
Python代码：

import numpy as np
def softmax_t(x,t):
	x_exp = np.exp(x / t)
	return x_exp / np.sum(x_exp)

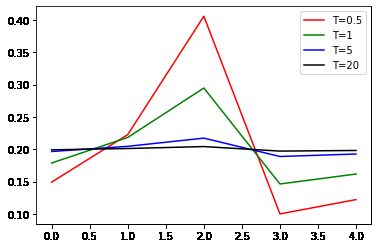
$q_i$代表第$i$类的输出概率，$z_i$和$z_j$为softmax的输入，即上一层神经元的输出(logits)，T表示temperature参数。通常情况下，我们使用的softmax函数T为1，但$T$可以控制输出soft的程度。比如对于$z=[0.3,0.5,0.8,0.1,0.2]$，我们分别取$T=[0.5,1,5,20]$，然后画出softmax函数的输出可以看到，$T$越小，输出的预测结果越“硬”（曲线更加曲折），T越大输出的结果越“软”（曲线更加平和）。

插一句题外话，为什么这里的参数是叫温度(temperature)呢？这和蒸馏(distillation)这一热力学工艺有关。在蒸馏工艺中，温度越高提取到的物质越纯越浓缩。而在知识蒸馏中，参数T越大（温度越高），teacher model产生的label越"soft"，信息熵就越高，提炼的知识更具有一般性(generalization)。所以说作者将这一参数取名temperature十分有趣。

知识蒸馏的实现过程可以概括为:

1. 训练teacher model；
2. 使用高温T将teacher model中的知识蒸馏到student model（在测试时温度T设为1）。

student modeld的目标函数由一下两项的加权平均组成：

1. distillation loss：soft targets（由teacher model产生） 和student model的soft predictions的交叉熵，这里的T使用的是和训练teacher model相同的值。（保证student model和teacher model的结果尽可能一致）
2. student loss：hard targets 和student model的输出数据的交叉熵，但T设置为1。（保证student model的结果和实际类别标签尽可能一致）

总体的损失函数可以写作：
$$\mathcal{L}(x,W)=\alpha \ast \text{CE}(y,\sigma (z_s;T=1))+\beta \ast \text{CE}(\sigma (z_t;T=\tau ),\sigma (z_s,T=\tau ))$$
其中，$x$表示输入，$W$表示student model的参数，$y$是ground-truth label，$\text{CE}$是交叉熵损失函数，$\sigma$是刚刚提到的softmax temperature激活函数，$z_s$和$z_t$分别表示student和teacher model神经元的输出(logits), $\alpha$和$\beta$表示两个权重参数 [4].

原论文指出，$\alpha$要比$\beta$相对小一些可以取得更好的结果，因为在求梯度时soft targets被缩放了$1/T^2$，所以第2项要乘以一个更小的权值来平衡二者在优化时的比重 [1].

换一个角度来想，这里的知识蒸馏其实是相对于对于原始交叉熵添加了一个正则项：
$$\mathcal{L}(x,W)=\text{CE}(y,\hat{y})+\lambda \text{soft\_loss}(y^{\prime },\hat{y})$$
利用teacher model的先验知识对student model进行正则化 [5]。

本文原载于简书，未经授权，不得转载。

---

References:

[1] Distilling the Knowledge in a Neural Network.
[2] # Distilling the Knowledge in a Neural Network 论文笔记
[3] 深度神经网络模型蒸馏Distillation
[4] Knowledge Distillation
[5] 神经网络知识蒸馏 Knowledge Distillation