数据结构(逻辑结构、存储结构、顺序表，链表)学习笔记-day8

目录

前言

一、数据结构

1.1 数据相关

1.2 逻辑结构

1.3 存储结构

1.4 typedef关键字

二、线性表(顺序)

2.1 顺序表

2.2 顺序表操作(增删改查)

三、线性表(链表)

3.1 单向链表(无头操作)

3.2 单项链表操作(有头操作)

3.3 单项循环链表

3.4 双向链表及循环

总结

---

---

前言

今天主要学习数据结构，了解数据的逻辑结构、存储结构；线性表中的顺序表、链式表（单向链表、单向循环列表、双向表）；栈（顺序栈）和顺序队队列，代码量较大

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、数据结构

    (1)学习C语言是如何写程序,学习数据结构如何简洁高效的写程序
    (2)遇到一个实际问题，需要写程序，需要解决两个方面的问题

1.1 数据相关

       数据： 信息的载体，计算机的研究对象不再单纯是数值，研究的是数据间的关系及操作
数据元素：数据元素是数据的基本单位，由若干个基本项组成（学号、姓名、班级、学院）
节点： 数据元素就叫节点

1.2 逻辑结构

逻辑结构(构思阶段，找规律)

1.3 存储结构

逻辑结构在计算机上具体实现

 操作（运算）插入、删除、修改、检索

1.4 typedef关键字

 typedef关键字作用：类型重定义，增强程序可移植性

二、线性表(顺序)

2.1 顺序表

顺序表(数组，在内存当中连续存储，数据元素个数固定)
逻辑结构：线性结构  存储结构: 顺序存储  操作（运算）： 增 删 改 查

练习：int a[100] = {10,20,30,40,50};//部分初始化，当前的5个数，被称为有效元素个数  //post 代表位置, n代表有效元素的个数
    (1)insert_into_a(int *p, int post,int data);  //在第三个位置插入一个元素100， 有效元素个数+1;
 insert_into_a(a,3,1000)    //插入后变为  10 20 1000 30 40 50
    (2)print_a(int *p, int n);          //打印数组中元素（要求只打印有效元素） print_a(a,6);
    (3)delete_from_a(int *p, int n, int post);     //删除第四个位置的元素 有效元素个数-1;

#include 

//全局变量
int last = 5;//有效元素的个数是5

//打印数组，我只打印有效元素
void showArray(int *p)
{
	int i;
	for(i = 0; i < last; i++)
	{
		printf("%d ",p[i]);
	}
	printf("\n");
}
//删除指定位置的元素 int post 代表的是删除的是第几个元素
void deleteFromA(int *p, int post)
{
	int i;
	//1.先锁定整体向前移动元素的起始和终止下标
	//post ---- last-1
	for(i = post; i <= last-1; i++)
	{
		p[i-1] = p[i];
	}
	//2.有效元素的个数-1 
	last--;
}

//post 第几个位置  即将插入的数据
void insertIntoA(int *p, int post, int data)
{
	int i;
	//1.先确定整体向后移动的起始和终止下标
	//last - 1 ---- post -1
	for(i = last-1; i >= post-1; i--)
	{
		p[i+1] = p[i];
	}
	//2.将数据存入插入位置
	p[post-1] = data;
	//3.有效元素个数+1
	last++;
}
int main(int argc, const char *argv[])
{
	int a[100] = {10,20,30,40,50};
	showArray(a); // 10 20 30 40 50
	deleteFromA(a,3); // 10 20 40 50
	showArray(a); 
	insertIntoA(a,2,1000); // 10 1000 20 40 50
	showArray(a);
	return 0;
}

2.2 顺序表操作(增删改查)

 结构体重定义  宏定义  上代码！！

#include 
#include 

#define N 5

typedef struct 
{
	int data[N];//顺序表，用来存储数据
	int last;//代表当前顺序表中有效元素的个数
}seqlist_t;

//1.创建一个空的顺序表
seqlist_t *createEmptySeqlist()
{
	//1.申请结构体大小的空间 里面有一个 数组 和 一个int
	seqlist_t *p = malloc(sizeof(seqlist_t));
	if(p == NULL)
	{
		printf("malloc failed!!\n");
		return NULL;//空指针代表申请空间失败
	}
	//2.给结构体里面成员变量进行赋值
	p->last = 0;//空的表，所以有效元素个数0
	//3.将申请空间的首地址返回
	return p;
}
//2.向顺序表的指定位置插入数据
//post 第几个位置 x 插入的数据
int insertIntoSeqlist(seqlist_t *p,int post, int x)
{
	int i;
	//0.容错判断
	if(post < 1 || post > p->last+1 || isFullSeqlist(p))
	{
		printf("插入数据失败！！\n");
		return -1;//-1插入失败
	}
	//1.锁定需要整体向后移动的下标 
	// p->last-1 ----- post-1
	for(i = p->last-1; i >= post-1; i--)
	{
		p->data[i+1] = p->data[i];
	}
	//2.将插入的数据放入指定位置
	p->data[post-1] = x;
	//3.有效元素个数+1
	p->last++;
	return 0;//0表示插入成功
}
//3.遍历打印顺序表
void showSeqlist(seqlist_t *p)
{
	int i;
	for(i = 0; i < p->last; i++)
	{
		printf("%d ",p->data[i]);
	}
	printf("\n");
}

//4.判断顺序表是否为满 表满返回1 未满返回0
int isFullSeqlist(seqlist_t *p)
{
//	return p->last == N ? 1 : 0;//last有效元素个数 N数组长度
	return p->last == N;//C语言中真用1表达，假用0表达 条件为真，返回的值就是1，假就是0
}
//5.判断顺序表是否为空 表空返回1，表非空返回0
int isEmptySeqlist(seqlist_t *p)
{
	return p->last == 0;
}
//6.删除指定位置的数据 post 代表第几个
int deletePostSeqlist(seqlist_t *p, int post)
{
	int i;
	//0.容错判断 
	if(post < 1 || post > p->last || isEmptySeqlist(p))
	{
		printf("删除数据失败!!\n");
		return -1;
	}
	//1.先锁定整体向前移动元素的起始和终止下标
	//post ---- p->last-1
	for(i = post; i <= p->last-1; i++)
	{
		p->data[i-1] = p->data[i];
	}
	//2.删除之后，有效元素个数-1 
	p->last--;
	return 0;
}
//7.清空顺序表
void clearSeqlist(seqlist_t *p)
{
	p->last = 0;//将有效元素个数变为0
}
//8.求顺序表的长度
int getLengthSeqlist(seqlist_t *p)
{
	return p->last;
}
//9.查找指定数据出现的位置 x代表 被查找的数据
int searchDateSeqlist(seqlist_t *p, int x)
{
	int i;
	for(i = 0; i < p->last; i++)
	{
		if(p->data[i] == x)
			return i+1;//+1是因为 下标和第几个元素 差1 ,返回的是第几个位置
	}
	return -1;//-1代表没有找到
}

int main(int argc, const char *argv[])
{
	seqlist_t *p = createEmptySeqlist();
	insertIntoSeqlist(p,1,10);

	insertIntoSeqlist(p,1,20);
	insertIntoSeqlist(p,1,30);
	insertIntoSeqlist(p,1,40);
	showSeqlist(p);
	insertIntoSeqlist(p,5,50);
	showSeqlist(p);
	deletePostSeqlist(p,1);
	showSeqlist(p);
	printf("len is %d\n",getLengthSeqlist(p));
	printf("20的位置第%d个\n",searchDateSeqlist(p,20));
	free(p);
	return 0;
}		 

 顺序表插入删除麻烦，查找简单，因为每次插入、删除我们都需要移动数组，而查找则是利用数组的下标，可实现随机访问。

三、线性表(链表)

逻辑结构:  线性结构
存储结构:  链式存储结构 (在内存当中不是连续存储的)   顺序表通过数组下标访问数组元素，而链表是通过指针，同时存储结构不同。

3.1 单向链表(无头操作)

我们把单向链表的每个一个节点的数据域都认为是有效的，除了这个区别外，没有其他区别

#include 

struct node_t
{
	char data;//数据域
	struct node_t *next;//指针域
};
int main(int argc, const char *argv[])
{
	struct node_t A = {'A',NULL};//定义四个结构体变量
	struct node_t B = {'B',NULL};
	struct node_t C = {'C',NULL};
	struct node_t D = {'D',NULL};
	A.next = &B;//将四个节点，连接起来
	B.next = &C;
	C.next = &D;
	struct node_t *h = &A;//定义一个头指针，指向链表的第一个节点，也就头结点
	//用头指针来遍历无头单项链表
	while(h != NULL)
	{
		printf("%c ",h->data);
		h = h->next;
	}
	printf("\n");
	return 0;
}

3.2 单项链表操作(有头操作)

我们把单向链表的第一个节点视为无效的，此时的第一个节点称为头节点

#include 

struct node_t
{
	char data;//数据域
	struct node_t *next;//指针域
};
int main(int argc, const char *argv[])
{
	struct node_t S = {'S',NULL}; //有头单向链表的头节点
	//定义四个结构体变量
	struct node_t A = {'A',NULL};
	struct node_t B = {'B',NULL};
	struct node_t C = {'C',NULL};
	struct node_t D = {'D',NULL};
	//将四个节点，连接起来
	A.next = &B;
	B.next = &C;
	C.next = &D;
	S.next = &A;//将头节点连在无头链表的前面
	struct node_t *h = &S;//定义一个头指针，指向链表的第一个节点，也就头结点
	//用头指针来遍历有头单项链表
	while(h->next != NULL)
	{
		h = h->next;
		printf("%c ",h->data);
	}
	printf("\n");
	return 0;
}

 练习：写一个有头单向链表，一直输入学生成绩，存入链表中，直到输入-1 结束程序,每输入一个学生成绩，就malloc申请一个新的节点，将输入的成绩保存到数据域，并将该节点链接到链表尾巴

#include 
#include 
struct node_t
{
	int data;
	struct node_t *next;
};

int main(int argc, const char *argv[])
{
	int score;//用来保存输入的学生成绩
	//1.创建有头单向链表的头结点
	struct node_t *ptail = NULL;//ptail永远指向当前链表的尾巴
	struct node_t *pnew = NULL;//pnew 永远指向新创建的节点
	struct node_t *h = malloc(sizeof(struct node_t));
	if(NULL == h)
	{
		printf("malloc failed");
		return -1;
	}
	h->next = NULL;

	ptail = h; //最开始链表只有一个头节点，所以头节点也是尾节点，ptail指向当前的尾巴

	//2.循环输入成绩，每输入一个成绩，就创建一个新的节点，保存成绩并将新的节点连接在链表的尾巴上
	while(1)
	{
		printf("Please input student score:\n");
		scanf("%d",&score);
		if(score == -1)
			break;	
		//创建新的节点，将成绩保存到新的节点中
		pnew = malloc(sizeof(struct node_t));
		if(NULL == pnew)
		{
			printf("malloc failed\n");
			return -1;
		}
		//给新创建的节点赋值
		pnew->data = score;
		pnew->next = NULL;
		//将这个新节点连接在链表的尾巴上
		ptail->next = pnew;//将新节点，连接在链表的尾巴上
		ptail = pnew;//或者写ptail = ptail->next 
		//由于连接新的节点，新的节点就是当前链表的尾节点,移动ptail，使ptail永远指向当前链表的尾巴
	}
	//遍历有头链表
	while(h->next != NULL)
	{
		h = h->next;
		printf("%d ",h->data);
	}
	printf("\n");
	return 0;
}

 单向有头链表：

#include 
#include 

typedef struct node_t
{
	int data;//数据域
	struct node_t *next;//指针域
}linknode_t;

//1.创建空的链表
linknode_t *createEmptyLinklist()
{
	//创建一个节点，作为有头单向链表的头节点
	linknode_t *p = malloc(sizeof(linknode_t));
	//malloc函数的返回值 申请成功，返回的是申请空间的首地址
	if(NULL == p)//失败，返回的是空指针
	{
		printf("createEmptyLinklist malloc failed!!\n");
		return NULL;
	}
	p->next = NULL;//给节点赋值
	return p; 
}

//2.向链表的指定位置插入数据     post 插入的位置  x插入的数据
int insertIntoLinklist(linknode_t *p, int post, int x)
{
	int i;
	//0.对插入位置进行容错判断
	if(post < 1 || post > getLengthLinklist(p)+1)
	{
		printf("insertIntoLinklist failed!!\n");
		return -1;
	}
	//1.将头指针p移动到插入位置的前一个位置
	for(i = 0; i < post-1; i++) 
	{
		p = p->next;
	}
	//2.创建一个新的节点，保存数据
	linknode_t *pnew = malloc(sizeof(linknode_t));
	if(NULL == p)
	{
		printf("malloc failed!!\n");
		return -1;
	}
	//给新节点装数据
	pnew->data = x;
	pnew->next = NULL;
	//将新节点链接到链表中,先连后面，再连前面
	pnew->next = p->next;
	p->next = pnew;
	return 0;

}

//3.遍历打印链表
void showLinklist(linknode_t *p)
{
	while(p->next != NULL)
	{
		p = p->next;
		printf("%d ",p->data);
	}
	printf("\n");
}
//4.求链表的长度
int getLengthLinklist(linknode_t *p)
{
	int count = 0;
	while(p->next != NULL)
	{
		p = p->next;
		count++;
	}
	return count;
}
//5.判断单向链表是否为空 空返回1 非空返回0
int isEmptyLinklist(linknode_t *p)
{
	return p->next == NULL;
}
//6.删除链表中指定位置的数据
int deletePostLinklist(linknode_t *p, int post)
{
	//0.对删除位置进行容错判断
	if(post < 1 || post > getLengthLinklist(p) || isEmptyLinklist(p))
	{
		printf("deletePostLinklist failed!!\n");
		return -1;
	}
	//1.将头指针移动到删除位置的前一个位置
	int i;
	for(i = 0; i < post-1; i++)
	{
		p = p->next;
	}
	//2.定义一个pdel指针，指向被删除的节点
	linknode_t * pdel = p->next;
	//3.跨过被删除节点
	p->next = pdel->next;
	//4.释放被删除的节点
	free(pdel);
	return 0;
}
//7.清空链表
void clearLinklist(linknode_t *p)
{
	linknode_t *pdel = NULL;
	while(p->next != NULL)//只要链表不为空，就进行砍头操作
	{
		//1.将头指针移动到删除位置的前一个位置
		//第1步可以省略，因为每次删除的头节点的下一个节点
		//也就意味着，头节点是每次删除节点的前一个位置p可以保持不动
		//2.定义一个pdel指向被删除的节点
		pdel = p->next;
		//3.跨过被删除的节点
		p->next = pdel->next;
		//4.释放被删除节点
		free(pdel);
	}
}

//8.查找指定数据出现的位置，出现在第几个位置
//x代表的是被查找的数据
int searchDatePostLinklist(linknode_t *p,int x)
{
	int i = 0;
	while(p->next != NULL)
	{
		p = p->next;
		i++;
		if(p->data == x)
		{
			return i;
		}
	}
	return -1;//-1代表没有找到
}

int main(int argc, const char *argv[])
{
	linknode_t *h = createEmptyLinklist();	
	insertIntoLinklist(h,1,10);
	insertIntoLinklist(h,1,20);
	insertIntoLinklist(h,1,30);
	insertIntoLinklist(h,1,40);
	showLinklist(h);
	printf("30的位置是第%d个\n",searchDatePostLinklist(h,30));
	printf("len is %d\n",getLengthLinklist(h));
	deletePostLinklist(h,3);
	showLinklist(h);
	clearLinklist(h);
	printf("len is %d\n",getLengthLinklist(h));
	showLinklist(h);
	return 0;
}

 总结顺序表与链表的区别：对顺序表的操作本质是操作数组；链表是指针，对比一下二者的结构体，便可一目了然。

3.3 单项循环链表

##单向循环链表 案例代码举例

#include 

typedef struct node_t
{
	int data;//数据域
	struct node_t* next;//指针域,指向下一个节点的指针
}link_node_t;

int main(int argc, const char *argv[])
{
	//定义三个节点
	struct node_t a = {11,NULL};
	struct node_t b = {22,NULL};
	struct node_t c = {33,NULL};
	//将三个节点连接在一起
	a.next = &b;
	b.next = &c;
	//用循环遍历 无头单向链表,将每个节点的数据域打印输出
	struct node_t* p = &a;

	c.next = p;//将无头链表的最后一个节点的next指针,指向第一个节点,形成单向循环链表   或者c.next = &a;

	while(1)
	{
		printf("%d\n",p->data);
		p = p->next;
		sleep(1);//每隔1s打印一次
	}
	return 0;
}

练习：使用单向循环链表解决约瑟夫问题

#include 
#include 

typedef struct node_t
{
	int data;
	struct node_t* next;
}link_node_t;

int main(int argc, const char *argv[])
{
	int i;
	int all_num = 8;//猴子的总数
	int start_num = 3;//开始数数的猴子号码
	int out_num = 4;//出局猴子的号码
	printf("请您输入猴子的总数, 起始报数号码, 杀死号码:\n");
	scanf("%d%d%d",&all_num,&start_num,&out_num);
	//1.形成一个单向循环链表,每个节点都是malloc
	link_node_t* pnew = NULL;//永远指向新创建的节点
	link_node_t* phead = (link_node_t*)malloc(sizeof(link_node_t));
	if(phead == NULL)
	{
		printf("phead malloc failed!!\n");
		return -1;
	}
	//给第一个节点装上数据 1号猴子
	phead->data = 1;//1号猴子
	phead->next = NULL;
	//将剩余的2 ---- all_num 号码,每个都创建节点,插入的在链表的尾巴
	//尾插法:核心思想:有一个尾指针,永远指向当前链表的尾巴
	link_node_t* ptail = phead;//ptail永远指向新表的尾巴,因为只有一个节点的时候,既是头节点又是尾节点
	for(i = 2; i <= all_num; i++)// i 2 3 4 5 6 7 8
	{
		//创建新的节点
		pnew = (link_node_t*)malloc(sizeof(link_node_t));
		if(pnew == NULL)
		{
			printf("pnew malloc failed!!\n");
			return -1;
		}
		//新的节点装上猴子的号码
		pnew->data = i;
		pnew->next = NULL;
		//将新节点插入在链表的尾巴上
		ptail->next = pnew;
		//连接之后链表变长,继续移动尾指针,移动到当前链表的尾巴上
		ptail = pnew;//或者ptail = ptail->next
	}
	//形成单向循环链表
	ptail->next = phead;//最后一个节点的next指针,指向第一个节点
	
	
#if 0
	//调试程序
	while(1)
	{
		printf("%d\n",phead->data);
		phead = phead->next;
		sleep(1);
	}
#endif
	//2.在循环杀猴前,需要将头指针移动到开始报数的猴子节点上
	for(i = 0; i < start_num-1; i++)//不要问我为什么start_num - 1 自己画图找规律
		phead = phead->next;
	//3.循环杀猴
	while(phead != phead->next)//phead == phead->next 循环结束 最终环里面会剩下一个猴子,也就是一个节点,节点的next指针和头指针相等
	{
		//将头指针移动到删除位置的前一个位置
		for(i = 0; i < out_num-2; i++)//不要问我为什么out_num - 2 自己画图找规律
			phead = phead->next;
		//定义一个pdel指针变量,指向被删除节点
		link_node_t* pdel = phead->next;
		//跨过删除节点
		phead->next = pdel->next;
		printf("kill is %d\n",pdel->data);//调试程序,看看杀猴的顺序是否符合逻辑
		//释放删除节点
		free(pdel);

		//因为杀死猴子后,要从删除位置的下一个位置开始报数,phead原来指向的
		//删除位置的前一个位置,所以phead = phead->next向后移动一个位置
		phead = phead->next;
	}
	printf("Monkey King is %d\n",phead->data);
	return 0;
}

 插入的时候:先连后面(pnew->next 指针先被赋值)，再连前面（p->next指针被赋值）

练习：递增有序的链表A  1 3 5 7 9 10   递增有序的链表B  2 4 5 8 11 15  新链表：1 2 3 4 5 5 7 8 9 10 11 15     将链表A和B合并，形成一个递增有序的新链表  //尾插法
编程思想：同时遍历两条链表，谁小就将这个节点插入在新链表的尾巴上

方法1：创建新的头指针

//合并表A和表B
link_node_t* combineAB(link_node_t* pa, link_node_t* pb)
{
	link_node_t* temp1 = NULL;
	link_node_t* temp2 = NULL;
	temp1 = pa;
	temp2 = pb;
	pa = pa->next;
	pb = pb->next;
	free(temp1); //将pa的头节点释放
	free(temp2); //将pb的头节点释放
	
	//创建一个新的节点,作为新表的表头
	link_node_t* phead = (link_node_t*)malloc(sizeof(link_node_t));
	if(phead == NULL)
	{
		printf("phead malloc failed!!\n");
		return NULL;
	}
	link_node_t* ptail = phead;//尾插法,所以有个尾指针,指向当前链表的尾巴

	//pa 和 pb是两张无头单向链表的头指针
	//同时遍历两张无头的单向链表 while(p != NULL)
	while(pa != NULL && pb != NULL)
	{
		//谁小就把谁的节点,插入在新链表的尾巴上
		if(pa->data < pb->data)
		{
			ptail->next = pa;//将pa的节点,插入在尾巴上
			ptail = ptail->next;//因为插入在尾巴后,新表边长,尾指针向后移动,指向当前表的尾巴
			pa = pa->next;//下一次循环,用pa的下一个节点与pb左比较
		}
		else
		{
			ptail->next = pb;//将pb的节点,插入在尾巴上
			ptail = ptail->next;//因为插入在尾巴后,新表边长,尾指针向后移动,指向当前表的尾巴
			pb = pb->next;//下一次循环,用pb的下一个节点与pa左比较
		}
	}
	//上面的循环结束后,必然有其中一条链表遍历完成，我们需要做出判断那条链表有剩余
	if(pa == NULL)//说明pb有剩余
		ptail->next = pb;//将pb剩余的尾巴接上
	else//说明pa有剩余 
		ptail->next = pa;//将pa剩余的尾巴接上
	return phead;
}

int main(int argc, const char *argv[])
{
	link_node_t* pa = createEmptyLinklist();
	link_node_t* pb = createEmptyLinklist();
	insertIntoLinklist(pa, 1, 1);
	insertIntoLinklist(pa, 2, 3);
	insertIntoLinklist(pa, 3, 5);
	insertIntoLinklist(pa, 4, 7);
	insertIntoLinklist(pa, 5, 9);
	insertIntoLinklist(pa, 6, 10);
	insertIntoLinklist(pb, 1, 2);
	insertIntoLinklist(pb, 2, 4);
	insertIntoLinklist(pb, 3, 5);
	insertIntoLinklist(pb, 4, 8);
	insertIntoLinklist(pb, 5, 11);
	insertIntoLinklist(pb, 6, 15);
	showLinklist(pa);
	showLinklist(pb);
	link_node_t* h = combineAB(pa,pb);
	showLinklist(h);
	return 0;
}

方法2：用已经创建新的表头pA或pB，作为新表的表头，完成合并链表

void combineAB(link_node_t* pa, link_node_t* pb)
{
	link_node_t* ptail = NULL;
	//1.ptail指向新链表的尾巴
	ptail = pa;//将表Ａ当做合并后新链表的头,ptail永远指向新链表的尾巴

	//当前的新链表只有一个头节点，头节点也是尾节点
	//ptail = pb;//相当于拿表b的头，当成新表的头

	//2.移动一下pa和pb将表Ａ和表Ｂ看成两个无头的单向链表
	pa = pa->next;
	pb = pb->next;
	//3.同时遍历两张无头单向链表,谁小就将谁连接到新链表的尾巴上
	while(pa != NULL && pb != NULL)
	{
		if(pa->data < pb->data)
		{
			//需要将pa指向的这个节点小，需要连接到新链表的尾巴
			ptail->next = pa;//连接到尾巴上
			pa = pa->next;//连接之后，ｐａ指向下一个节点，准备下一轮与表ｂ的比较
			ptail = ptail->next;//ptail永远指向当前链表的尾巴
		}
		else
		{
			ptail->next = pb;
			pb = pb->next;
			ptail = ptail->next;
		}
	}
	//4.循环结束后，肯定有一个表先遍历完成
	if(pa == NULL)//说明表Ａ遍历完成，表Ｂ有剩余
		ptail->next = pb;//将表ｂ剩余没遍历完的部分，接到新链表的尾巴上
	else//说明表ｂ遍历完成，表Ａ有剩余
		ptail->next = pa;
	
}

int main(int argc, const char *argv[])
{
	link_node_t* ha = createEmptyLinklist();
	insertIntoLinklist(ha,1,1);
	insertIntoLinklist(ha,2,3);
	insertIntoLinklist(ha,3,5);
	insertIntoLinklist(ha,4,7);
	insertIntoLinklist(ha,5,9);
	insertIntoLinklist(ha,6,10);
	showLinklist(ha);
	link_node_t* hb = createEmptyLinklist();
	insertIntoLinklist(hb,1,2);
	insertIntoLinklist(hb,2,4);
	insertIntoLinklist(hb,3,5);
	insertIntoLinklist(hb,4,8);
	insertIntoLinklist(hb,5,11);
	insertIntoLinklist(hb,6,15);
	showLinklist(hb);
	combineAB(ha,hb);
	showLinklist(ha);
	return 0;
}

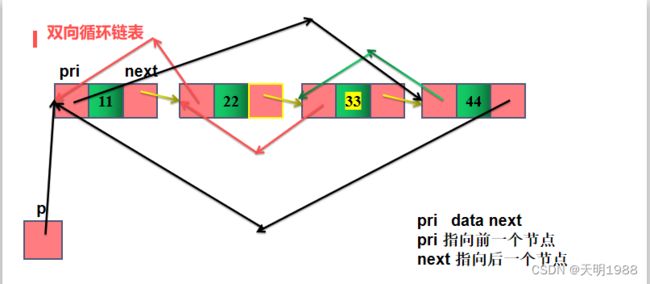
3.4 双向链表及循环

总结

这里对今天所学数据结构进行总结：主要学习数据结构，了解数据的逻辑结构、存储结构；线性表中的顺序表、链式表（单向链表、单向循环列表、双向表）；栈（顺序栈）和顺序队队列以及相应的本质，代码量较大，加油！！