OpenCV之傅里叶描述子特征构建（Fourier Descriptor）

1、傅里叶描述子介绍

傅里叶描述子是一种图像特征，用来描述轮廓的特征参数。

傅里叶描述子的基本思想是：首先我们设定物体的形状轮廓是一条闭合的曲线，一个点沿边界曲线运动，假设这个点为p(l)，它的复数形式的坐标为x(l)+jy(l)，它的周期是这个闭合曲线的周长，这也表明属于一个周期函数。该以曲线周长作为周期的函数能够通过傅里叶级数表示。在傅里叶级数里面的多个系数z(k)与闭合边界曲线的形状有着直接关系，将其定义为傅里叶描述子。当取到足够阶次的系数项z(k)时，傅里叶描述子能够完全提取形状信息，并恢复物体的形状。
也就是说，傅里叶描述子用一个向量表示轮廓，将轮廓数字化，从而能更好的区分不同的轮廓，达到识别物体的目的。傅里叶描述子的特点是简单并且非常高效，是识别物体形状的重要方法之一。

简单来说，傅里叶描述子就是用一个向量代表一个轮廓，将轮廓数字化，从而能更好地区分不同的轮廓，进而达到识别物体的目的。

如上图所示，少数的傅里叶描述子就可以用于捕获边界的大体特征。这一性质很有用，因为这些系数携带有形状信息。

2、归一化的傅里叶描述子

事物轮廓曲线的初始点、 尺寸及方向会影响傅里叶描述子的大小。 当识别事
物存在尺度改变、 旋转等运动时， 要通过归一化的方法处理描述子，进而使傅里叶描述子具有旋转、平移和尺度变换不变性的特性，这就是归一化的傅里叶描述子。

总结：傅立叶描述子可以很好地描述物体的轮廓特征，并且只需少量的描述子（即向量中的数不需要太多）即可大致代表整个轮廓。其次，对傅立叶描述子进行简单的归一化操作后，即可使描述子具有平移、旋转、尺度不变性，即不受轮廓在图像中的位置、角度及轮廓的缩放等影响，是一个鲁棒性较好的图像特征。

3、算法描述

【注意】：一般情况下，我们在计算傅里叶描述子前，首先需要进行图像去噪、二值化、形态学处理等若干步骤，以尽可能减小噪声。经过一系列处理后，可以利用findContours和drawContours函数进行轮廓提取与绘制，

如上图所示，
空间域描述该轮廓：
$s(k)=[x(k),y(k)],k=0,1,2,...,K-1$
如果把空间平面转换到复平面，轮廓点描述为：
$s(k)=x(k)+jy(k),k=0,1,2,...,K-1$，也就是说x轴为复数序列的实轴，y轴为复数序列的虚轴。复数域下，二维问题简化为一维问题，但边界本质未变。

对图像轮廓点$s(k)=x(k)+jy(k)$,其离散傅里叶变换（DFT）为$a(u)={\sum }_{k=0}^{K-1}s(k)e^{-j2\pi uk/K},u=0,1,2,...,K-1$
其中的复系数a(u)称为边界的傅里叶描绘子。

这些系数的反傅里叶变换可恢复s(k)。也就是说，$s(k)=\frac{1}{K}{\sum }_{u=0}^{P-1}a(u)e^{j2\pi uk/P},k=0,1,2,...,K-1$

【注意】：图像中的细节对应高频，平缓区域由低频决定。

而轮廓全局由低频决定，轮廓细节由高频决定。物体分类用轮廓全局就可以了，即只需要s(k)的低频部分（即u的取值从0到P-1）：$\hat{s}(k)=\frac{1}{K}{\sum }_{u=0}^{P-1}a(u)e^{j2\pi uk/P},k=0,1,2,...,K-1$

注意，其中近似恢复的轮廓点$\hat{s}(k)$的点数和原轮廓点的数量一样都是K个。只有近似的轮廓只是对元轮廓进行大致“描绘”，且描述子只有P(P
而且P取得越小，细节部分丢失得越多。

4、代码示例

话不多说，直接上代码：

#include
#include  
#include
#include 
using namespace cv;
using namespace std;
int main()
{
	//读取图像
	Mat src_image = imread("D:\\Desktop\\1.png");
	//图像读取出错处理
	if (!src_image.data)
	{
		cout << "src image load failed!" << endl;
		system("pause");
		return -1;
	}
	//显示源图像
	namedWindow("原图", WINDOW_NORMAL);
	imshow("原图", src_image);

	//高斯滤波
	GaussianBlur(src_image, src_image, Size(15, 15), 0);
	//imshow("GaussianBlur", blur_image);

	/*灰度变换与二值化*/
	Mat gray_image, binary_image;
	cvtColor(src_image, gray_image, COLOR_BGR2GRAY);
	threshold(gray_image, binary_image, 30, 255, THRESH_BINARY | THRESH_TRIANGLE);
	/*imshow("binary", binary_image);*/

	/*形态学闭操作*/
	Mat morph_image;
	Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3), Point(-1, -1));
	morphologyEx(binary_image, morph_image, MORPH_CLOSE, kernel, Point(-1, -1), 2);
	/*imshow("morphology", morph_image);*/
	
	//Canny算子边缘检测
	Canny(morph_image, morph_image, 100, 250);//canny算子边缘检测
	imshow("处理后图像", morph_image);

	//Mat new_image=find_contours(morph_image);
	//imshow("最大轮廓", new_image);

	/*查找外轮廓*/
	vector< vector<Point> > contours;
	vector<Vec4i> hireachy;
	findContours(morph_image, contours, hireachy, CV_RETR_EXTERNAL, CHAIN_APPROX_NONE, Point());
	//寻找最大轮廓，即目标轮廓
	vector<double> g_dConArea(contours.size());
	for (int i = 0; i < contours.size(); i++)
	{
		//绘制轮廓
		/*drawContours(imageContours0, contours, i, Scalar(255), 1, 8, hierarchy);*/
		//计算轮廓的面积
		g_dConArea[i] = contourArea(contours[i]);
		//cout << "【用轮廓面积计算函数计算出来的第" << i << "个轮廓的面积为：】" << g_dConArea[i] << endl;
	}
	//寻找面积最大的部分
	int idx = 0;
	for (int i = 1; i < contours.size(); i++) {
		if (g_dConArea[i] > g_dConArea[idx]) {
			idx = i;
		}
	}
	//画出目标轮廓
	Mat result_image = Mat::zeros(morph_image.size(), CV_8UC1);
	/*draw_contours.push_back(contours[idx]);*/
	drawContours(result_image, contours, idx, Scalar(255), 2, 8, hireachy);
	imshow("最终结果", result_image);

	//计算轮廓的傅里叶描述子
	Point p;
	int x, y, s;
	int i = 0, j = 0, u = 0;
	float f[9000];//轮廓的实际描述子
	float fd[16];//归一化后的描述子，并取前15个
	s = (int)contours[idx].size();//轮廓点组的规格
	Mat src1(Size(s, 1), CV_8SC2);//s行1列的Mat对象
	for (u = 0; u < s; u++)
	{
		float sumx = 0, sumy = 0;
		for (j = 0; j < s; j++)
		{
			p = contours[idx].at(j);
			x = p.x;
			y = p.y;
			sumx += (float)(x*cos(2 * CV_PI*u*j / s) + y * sin(2 * CV_PI*u*j / s));
			sumy += (float)(y*cos(2 * CV_PI*u*j / s) - x * sin(2 * CV_PI*u*j / s));
		}
		src1.at<Vec2b>(0, u)[0] = sumx;//0行u列第0通道值
		src1.at<Vec2b>(0, u)[1] = sumy;//0行u列第1通道值
		f[u] = sqrt((sumx*sumx) + (sumy*sumy));
	}
	//傅立叶描述子的归一化，取前15个
	f[0] = 0;
	fd[0] = 0;
	for (int k = 2; k < 17; k++)
	{
		f[k] = f[k] / f[1];
		fd[k - 1] = f[k];
		cout << fd[k - 1] << endl;
	}
	//保存数据
	ofstream ofs;
	for (int k = 1; k < 16; k++)
	{
		ofs.open("D:\\Desktop\\1.txt", ios::app);
		ofs <<setiosflags(ios::fixed) << setprecision(6) <<fd[k] << endl;//设置精度，小数点后保留六位
		ofs.close();
	}
	waitKey();
	return 0;
}

前面就不进行过多介绍了，这里重点介绍一下傅里叶描述子相关部分，如果前面轮廓部分还不清楚，可以参考博客：
OpenCV之轮廓查找与绘制（findContours和drawContours函数详解）和OpenCV之查找并绘制最大轮廓及绘制轮廓的外接矩形。

很多人不明白下列两行代码：

sumx += (float)(x*cos(2 * CV_PI*u*j / s) + y * sin(2 * CV_PI*u*j / s));
sumy += (float)(y*cos(2 * CV_PI*u*j / s) - x * sin(2 * CV_PI*u*j / s));

它的基本意思如下：

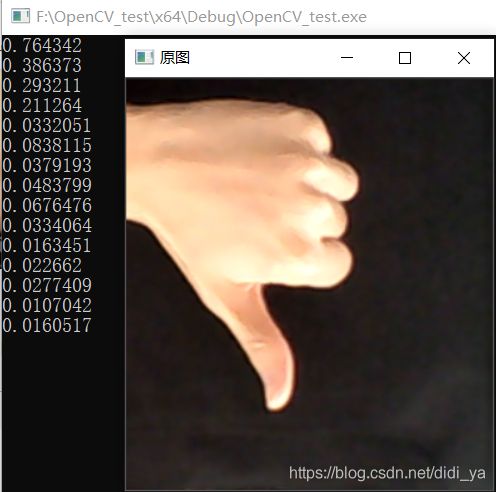
输出结果：
原始图像：

处理后的图像：

最终结果：

傅里叶描述子：

而将图像翻转，即：

左右翻转：

上下翻转：

对角线翻转：

可以发现，四次得到的傅里叶描述子基本类似，这也是傅里叶描述子的优势之一。

如果对你有所帮助，记得点个赞哟~

参考：
1.《基于傅里叶描述子的物体形状识别的研究》