软件工程经济学第三章作业
软件工程经济学第三章作业
仅供参考,请自行核对,切勿直接抄袭
第三题
某软件公司拟开发一城市社区管理信息系统(MIS)。根据概要设计,该MIS由 N 1 、 N 2 、 N 3 、 N 4 和 N 5 N_1、N_2、N_3、N_4和N_5 N1、N2、N3、N4和N5五个功能子系统构成,项目组根据经验及公司信息库的资料确定各子系统工作量的最小可能值 a j a_j aj、最大可能值 b j b_j bj和最可能值 m j m_j mj(单位:行)及成本费用率 C o j C_{oj} Coj(单位:元/行)、劳动生产率 E o j E_{oj} Eoj(单位:行/人月)(j=1,…,5),见表3.27。此外,在系统的需求分析、系统设计、编码、测试四个阶段的工时费用率α(单位:元/人月)和子系统在上述各阶段的工作量估计 M ~ i 1 , M ~ i 2 , M ~ i 3 , M ~ i 4 , \widetilde{M}_{i1},\widetilde{M}_{i2},\widetilde{M}_{i3},\widetilde{M}_{i4}, M i1,M i2,M i3,M i4,(单位:人月),i=1,…,5,见表3.28。试利用功能分解法对该MIS作成本与工作量估算。
答:(3.27表格中的顺序是上一版书的,老师PPT也是这个,最新版的顺序 b j b_j bj和 m j m_j mj应该调过来(接下来也以最新版的来计算)
1️⃣ 由表3.27可计算各个子系统的以行为单位的工作量 E j E_j Ej、以人月为单位的工作量 M j M_j Mj以及成本 C j C_j Cj,j=1,…,5
对于子系统 N 1 N_1 N1,可计算
期望(平均)工作量 E 1 E_1 E1有
E 1 = a 1 + 4 m 1 + b 1 6 = 2200 + 4 × 2360 + 2490 6 = 2355 行 E_1=\frac{a_1+4m_1+b_1}{6}=\frac{2200+4\times 2360+2490}{6}= 2355行 E1=6a1+4m1+b1=62200+4×2360+2490=2355行
成本有: C 1 = C o 1 E 1 = 15 × 2355 = 35325 元 C_1=C_{o1}E_1=15\times 2355=35325元 C1=Co1E1=15×2355=35325元
以人月为单位的工作量有
M 1 = E 1 E o 1 = 2355 314 = 7.5 人 月 M_1=\frac{E_1}{E_{o1}}=\frac{2355}{314}=7.5人月 M1=Eo1E1=3142355=7.5人月
同理可得到子系统 N 2 , N 3 , N 4 , N 5 N_2,N_3,N_4,N_5 N2,N3,N4,N5的相关值如下:
| 子系统 | E j E_j Ej/行 | C j C_j Cj/元 | M j M_j Mj/人月 |
|---|---|---|---|
| N 1 N_1 N1 | 2355 | 35325 | 7.5 |
| N 2 N_2 N2 | 5280 | 105600 | 24 |
| N 3 N_3 N3 | 6820 | 150040 | 31 |
| N 4 N_4 N4 | 3360 | 60480 | 14 |
| N 5 N_5 N5 | 2100 | 63000 | 15 |
则系统的总成本 C s C_s Cs和总工作量 E s , M s E_s,M_s Es,Ms分别为:

2️⃣ 由表3.28计算系统在生命周期各阶段的工作量 M ~ k \widetilde{M}_k M k和成本 C ~ k \widetilde{C}_k C k,j=1,…,4
同理可得系统设计、编码、测试的工作量和成本
| 分析阶段 | M ~ k \widetilde{M}_k M k | C ~ k \widetilde{C}_k C k |
|---|---|---|
| 需求分析1 | 9.0 | 45000 |
| 系统设计 | 36 | 172800 |
| 编码 | 17.5 | 74375 |
| 测试 | 33 | 148500 |
则系统的总成本 C ~ s \widetilde{C}_s C s和总工作量 M ~ s \widetilde{M}_s M s分别为
C ~ s = ∑ k = 1 4 C ~ k = 440675 元 M ~ s = ∑ k = 1 4 M ~ i k = 95.5 人 月 \widetilde{C}_s=\sum_{k=1}^4\widetilde{C}_k=440675\ 元\\ \widetilde{M}_s=\sum_{k=1}^4\widetilde{M}_{ik}=95.5\ 人月 C s=k=1∑4C k=440675 元M s=k=1∑4M ik=95.5 人月
3️⃣ 取上述两组数据的保守值作为系统成本和工作量的估算值,即
C ~ s = 440675 元 M ~ s = 95.5 人 月 \widetilde{C}_s=440675\ 元\\ \widetilde{M}_s=95.5\ 人月 C s=440675 元M s=95.5 人月
第四题
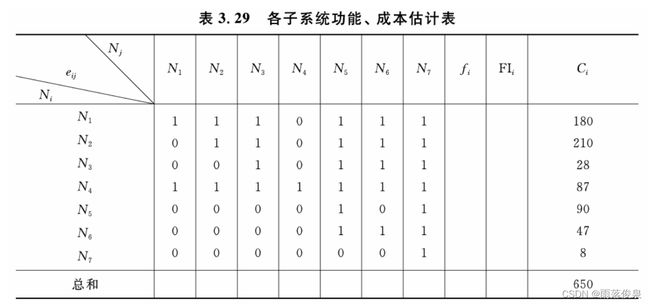
某大型测控系统根据概要设计,拟由 N 1 、 N 2 、 N 3 、 N 4 、 N 5 、 N 6 和 N 7 N_1、N_2、N_3、N_4、N_5、N_6和N_7 N1、N2、N3、N4、N5、N6和N7,七个功能子系统构成,项目组根据各子系统功能重要性的两两比较,可得如表3.29所示的有关数据。其中, f i f_i fi称为子系统 N i N_i Ni的功能重要性得分,并有 f i = ∑ j = 1 7 e i j , i = 1 , … , 7 f_i=∑_{j=1}^7e_{ij},i=1,…,7 fi=∑j=17eij,i=1,…,7。试由 f i f_i fi计算子系统 N i N_i Ni的功能系数 FI i = f i / ∑ j = 1 7 f i \text{FI}_i=f_i/\sum_{j=1}^7f_i FIi=fi/∑j=17fi于表3.29第十列。此外,项目组对各子系统的成本估计初值 C i C_i Ci(单位:万元)于表3.29。若该测控系统的目标成本已确定为650万元,试利用价值工程法对该测控系统做目标成本分解和进行功能/成本分析。
答:
由表3.29可知
| N i N_i Ni | f i f_i fi | FI i \text{FI}_i FIi |
|---|---|---|
| N 1 N_1 N1 | 6 | 0.2143 |
| N 2 N_2 N2 | 5 | 0.1786 |
| N 3 N_3 N3 | 4 | 0.1429 |
| N 4 N_4 N4 | 7 | 0.2500 |
| N 5 N_5 N5 | 2 | 0.0714 |
| N 6 N_6 N6 | 3 | 0.1071 |
| N 7 N_7 N7 | 1 | 0.0357 |
| 总和 | 28 | 1 |
由公式 CI i = C i / ∑ i = 1 7 C i \text{CI}_i=C_i/\sum_{i=1}^7C_i CIi=Ci/∑i=17Ci可得子系统的成本系数,由 VI i = FI i / CI i \text{VI}_i=\text{FI}_i/\text{CI}_i VIi=FIi/CIi可得子系统的价值系数,可得下表
| 子系统 N i N_i Ni | 成本估值 C i C_i Ci/万元 | 成本系数 CI i \text{CI}_i CIi | 功能系数 FI i \text{FI}_i FIi | 价值系数 VI i \text{VI}_i VIi |
|---|---|---|---|---|
| N 1 N_1 N1 | 180 | 0.2769 | 0.2143 | 0.7739 |
| N 2 N_2 N2 | 210 | 0.3231 | 0.1786 | 0.5528 |
| N 3 N_3 N3 | 28 | 0.0431 | 0.1429 | 3.3173 |
| N 4 N_4 N4 | 87 | 0.1338 | 0.2500 | 1.8678 |
| N 5 N_5 N5 | 90 | 0.1385 | 0.0714 | 0.5157 |
| N 6 N_6 N6 | 47 | 0.0723 | 0.1071 | 1.4812 |
| N 7 N_7 N7 | 8 | 0.0123 | 0.0357 | 2.9006 |
| 总和 | 650 | 1 | 1 |
根据价值系数 V I i VI_i VIi之大小可进行如下的功能/成本分析:子系统 N 1 , N 2 , N 5 N_1,N_2,N_5 N1,N2,N5之价值系数 V I 1 、 V I 2 、 V I 5 < 1 VI_1、VI_2、VI_5<1 VI1、VI2、VI5<1,这意味着该子系统的原成本估值分配过高,应采取措施降低其成本,以促使功能与成本匹配;子系统 N 3 , N 4 , N 6 , N 7 N_3,N_4,N_6,N_7 N3,N4,N6,N7有 V I 3 , V I 4 , V I 6 , V I 7 > 1 VI_3,VI_4,VI_6,VI_7>1 VI3,VI4,VI6,VI7>1,此意味着子系统的成本估值偏小,应适当加大其成本来完善其功能
根据功能系数的大小,可对各子系统的原成本估值 C i C_i Ci进行调整
利用目标成本C=650万元计算出经调整后的计划成本 C ~ i \widetilde{C}_i C i,据此可计算各子系统原成本估计值经调整后的降低值,计算出各子系统新的成本系数 C I ~ i \widetilde{CI}_i CI i与各子系统新的价值系数 V I ~ i \widetilde{VI}_i VI i,可得下表
| 子系统 N i N_i Ni | 功能系数 FI i \text{FI}_i FIi | 新分配的计划成本 C ~ i \widetilde{C}_i C i/万元 | 原成本估值 C i C_i Ci/万元 | 应降低的成本额/万元 | 目标成本系数 C I ~ i \widetilde{CI}_i CI i | 目标价值系数 V I ~ i \widetilde{VI}_i VI i |
|---|---|---|---|---|---|---|
| N 1 N_1 N1 | 0.2143 | 139.2857 | 180 | 40.7143 | 0.2143 | 1 |
| N 2 N_2 N2 | 0.1786 | 116.0714 | 210 | 93.9286 | 0.1786 | 1 |
| N 3 N_3 N3 | 0.1429 | 92.8571 | 28 | -64.8571 | 0.1429 | 1 |
| N 4 N_4 N4 | 0.2500 | 162.5000 | 87 | -75.5000 | 0.25 | 1 |
| N 5 N_5 N5 | 0.0714 | 46.4286 | 90 | 43.5714 | 0.0714 | 1 |
| N 6 N_6 N6 | 0.1071 | 69.6429 | 47 | -22.6429 | 0.1071 | 1 |
| N 7 N_7 N7 | 0.0357 | 23.2143 | 8 | -15.2143 | 0.0357 | 1 |
| 总和 | 1 | 650 | 650 | 0 | 1 |
总成本未下降
第五题
考虑一个规模为32kDSI的半独立气象预报软件,根据该软件的目标与功能需求以及开发机构的人力资源投入状况,可得各影响因子 U j U_j Uj的等级如表3.30所示,又知该软件开发机构的工时费用率有α=3000元/人月。试利用中级 COCOMO模型对该软件的成本、工作量与工期作出估计。
答:
中级 COCOMO模型的公式如下:
{ C s = α ⋅ M s T d = h ( M s ) d M s = U ⋅ M o M o = r ⋅ L k U = ∏ 15 U j \begin{cases} C_s=\alpha\cdot M_s\\ T_d=h(M_s)^d\\ M_s=U\cdot M_o\\ M_o=r\cdot L^k\\ U=\prod^{15} U_j \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Cs=α⋅MsTd=h(Ms)dMs=U⋅MoMo=r⋅LkU=∏15Uj
其中 C s C_s Cs为软件开发成本(单位:美元);α为软件开发阶段的工时费用率(单位:美元/人月); M s M_s Ms为软件开发阶段的修正工作量(单位:人月); M o M_o Mo为软件开发阶段的基本工作量(单位:人月);L 为软件开发规模(单位:源指令千行数或kDSI);U 为软件综合影响因子(无量纲);Uj 为对成本有一定影响的第j个影响因子(无量纲),j=1~15; T d T_d Td为软件开发工期(单位:月);r,k,h,d为形式参数。
形式参数表如下:
15种影响软件工作量的因素 U j U_j Uj的等级分值表如下:
1️⃣ 由软件的基本特性(半独立型)可知:r=3.0 k=1.12 h=2.5 d=0.35
2️⃣ 由表3.30可得
| U 1 U_1 U1 | U 2 U_2 U2 | U 3 U_3 U3 | U 4 U_4 U4 | U 5 U_5 U5 | U 6 U_6 U6 | U 7 U_7 U7 | U 8 U_8 U8 | U 9 U_9 U9 | U 10 U_{10} U10 | U 11 U_{11} U11 | U 12 U_{12} U12 | U 13 U_{13} U13 | U 14 U_{14} U14 | U 15 U_{15} U15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.88 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
3️⃣ 则有
M o = r ⋅ L k = 3.0 × 3 2 1.12 ≈ 145.5 人 月 M_o=r\cdot L^k=3.0\times 32^{1.12}\approx145.5\ 人月 Mo=r⋅Lk=3.0×321.12≈145.5 人月
U = ∏ j = 1 15 U j = 0.88 U=\prod^{15}_{j=1} U_j=0.88 U=∏j=115Uj=0.88
M s = U ⋅ M o = 0.88 × 145.5 ≈ 128.0 人 月 M_s=U\cdot M_o=0.88\times 145.5\approx 128.0\ 人月 Ms=U⋅Mo=0.88×145.5≈128.0 人月
T d = h ( M s ) d = 2.5 × ( 128.0 ) 0.35 ≈ 13.7 月 T_d=h(M_s)^d=2.5\times (128.0)^{0.35}\approx13.7\ 月 Td=h(Ms)d=2.5×(128.0)0.35≈13.7 月
C s = α ⋅ M s = 3000 × 128.0 = 384000 元 C_s=\alpha\cdot M_s=3000\times 128.0=384 000\ 元 Cs=α⋅Ms=3000×128.0=384000 元
第八题
某通信网络测试设备其购买价格(原始价值)为5万元,预计使用五年,其残值估计为1000元。利用加速旧法求解该设备每年应摊入成本的各年设备折旧费。
答:
设 A t A_t At为设备在使用年限内第 t t t年的折旧额, t t t为设备使用的年数, T T T为设备使用年限, k 0 k_0 k0表示设备的原始价值, O O O表示设备若干年后的残值(预计), α α α表示设备的年基本折旧率,则加速旧法基本算法如下
A t = T + 1 − t ∑ j = 1 T j ( k 0 − O ) = T + 1 − t T ( T + 1 ) / 2 ( k 0 − O ) , t ≤ T A_t=\frac{T+1-t}{\sum_{j=1}^Tj}(k_0-O)=\frac{T+1-t}{T(T+1)/2}(k_0-O),t\le T At=∑j=1TjT+1−t(k0−O)=T(T+1)/2T+1−t(k0−O),t≤T
由于 k 0 = 50000 元 , T = 5 年 , O = 1000 元 k_0=50000\ 元,T=5\ 年,O=1000\ 元 k0=50000 元,T=5 年,O=1000 元
U = T + 1 − t T ( T + 1 ) / 2 = 6 − t 15 t = 1 , 2 , 3 , 4 , 5 k 0 − O = 50000 − 1000 = 49000 元 U=\frac{T+1-t}{T(T+1)/2}=\frac{6-t}{15}\quad t=1,2,3,4,5\\ k_0-O=50000-1000=49000\ 元 U=T(T+1)/2T+1−t=156−tt=1,2,3,4,5k0−O=50000−1000=49000 元
由加速旧法基本算法公式可得下表——计算机各年折旧额
| t | k o − O k_o-O ko−O | U = 6 − t 15 U=\frac{6-t}{15} U=156−t | A t = ( k 0 − O ) U A_t=(k_0-O)U At=(k0−O)U |
|---|---|---|---|
| 1 | 49000 | 5/15 | 16333.3 |
| 2 | 49000 | 4/15 | 13066.7 |
| 3 | 49000 | 3/15 | 9800 |
| 4 | 49000 | 2/15 | 6533.3 |
| 5 | 49000 | 1/15 | 3266.7 |
| 总计 | 1 | 49000 |
第十一题
某软件项目根据总体设计方案,它由N1、N2、……、 N7共七个功能模块构成,各模块根据其规模复杂性与功能、性能要求,可估计出模块成本详见表3.32。试利用ABC分类法寻找此软件项目成本控制的重点跟踪与控制模块。
答:
将各模块成本自大到小按序排列,设为 C i 1 ≥ C i 2 ≥ . . . ≥ C i 7 C_{i1}\ge C_{i2}\ge...\ge C_{i7} Ci1≥Ci2≥...≥Ci7并分别计算各对应模块的成本系数
CI i e = C i e C , C = ∑ j = 1 m e = 1 , 2 , . . . , 7 \text{CI}_{i_e}=\frac{C_{i_e}}{C},C=\sum_{j=1}^m\quad e=1,2,...,7 CIie=CCie,C=j=1∑me=1,2,...,7
| 模块 | N 3 N_3 N3 | N 2 N_2 N2 | N 1 N_1 N1 | N 7 N_7 N7 | N 6 N_6 N6 | N 5 N_5 N5 | N 4 N_4 N4 |
|---|---|---|---|---|---|---|---|
| 成本 | 21 | 19 | 15 | 13 | 10 | 7.5 | 6.5 |
| 成本系数 CI i e \text{CI}_{i_e} CIie | 0.228 | 0.206 | 0.163 | 0.141 | 0.109 | 0.082 | 0.071 |
| 累计成本系数 | 0.228 | 0.434 | 0.597 | 0.738 | 0.847 | 0.929 | 1 |
利用表格数据可画下图
此软件项目成本控制的重点跟踪与控制模块应该属于A类,即模块3,2,1,7