矩形排样问题 遗传算法解决方案
最近在实习中,遇到了一个实际问题。客户要将若干大小不一的小矩形,排到大矩形上,而且还要求可以设置小矩形之间的间距,和大矩形的margin值,便于裁切。
排样问题是一个经典的NP问题,有很多解决方案。神经网络、遗传、蚁群、模拟退火等等算法都可以解决这个问题。对于一些行业的工业生产,很多生产数据并没有测试数据那般刁钻,所以这些算法基本都能满足生产的需要。
在这里,我主要参考了一篇郑州大学的研究生毕业论文,自己又稍加了修改,用遗传算法解决了这个问题。
遗传算法的本质其实就是把问题简化为一个个序列,根据一定规律随机生成后,拿这个编码序列贪心的得出解,然后不断的迭代,优胜劣汰,向最优解靠拢。
我认为遗传算法有几个关键之处:编码规则、初始种群的选取、贪心方式、适应度函数的选择、变异规则。
1.好的编码规则能便于程序的实现,同时也决定了程序的贪心结构,在这里,我的编码是1-n的阿拉伯数字,代表放入的矩形的编号,从左到右是放入的顺序。如果矩形需要旋转,则为负数。
2.初始种群的选取,给矩形按照权值排序,权值=0.9*矩形面积+0.1*矩形长宽比,大的先放,小的后放,然后随机其正负值,生成初始种群,好的初始种群能很快就找到最优解。
3.我的贪心解决方案就是最低水平线算法,从左到右,从下到上,不断的寻找能放入的点。每次放入一个新点后,把未来的矩形可能的存在的点加入一个有序的序列中,后面的待排矩形就在这个序列里寻找可以放的点。
4.适应度函数,两个个体好坏的决定因素,在这里,我设置了3个决定因素,首先是放入的矩形面积占待放入的矩形面积的百分比,第二个是当前排入的矩形的最大高度,第三个是排入矩形的整齐程度(高的种类个数)。我还有一些新想法,比如比较新图形的重心,重心越靠左下约好,能避免一些相同适应值下的非最优解。
5.变异规则,这里用了4种变异方案,交叉、单点。。。。。。不详述了。
这里我把算法封装到了类里
#ifndef LAYOUTALGORYTHM_H
#define LAYOUTALGORYTHM_H
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
啊
#ifndef LAYOUTALGORYTHMGLOBAL_H
#define LAYOUTALGORYTHMGLOBAL_H
class LayoutAlgorythmGlobal
{
public:
static double m_weightArea;//矩形排序,面积权重
static double m_weightRatio;//矩形排序,长宽比权重
const static int m_members;//种群规模
const static int m_maxSize;//小矩形个数
static int m_iterCount;//最大迭代次数
static double m_pc1;//单点交叉概率
static double m_pc2;//两点交叉概率
static double m_pm1;//两点交换变异概率
static double m_pm2;//单点旋转变异概率
LayoutAlgorythmGlobal();
};
#endif // LAYOUTALGORYTHMGLOBAL_H
后面,就是实现这些东西了
void LayoutAlgorythm::solve()
{
//随机将前M个两两配对,产生后M个新个体,再排序,迭代50次
this->initialize();
int members=LayoutAlgorythmGlobal::m_members;
double Pc1=LayoutAlgorythmGlobal::m_pc1;
double Pc2=LayoutAlgorythmGlobal::m_pc2;
double Pm1=LayoutAlgorythmGlobal::m_pm1;
double Pm2=LayoutAlgorythmGlobal::m_pm2;
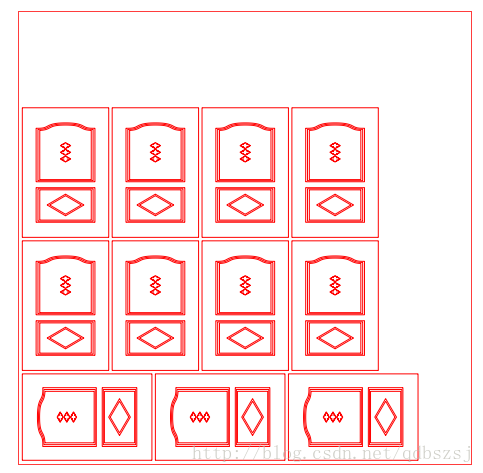
for(int i=0;i最后效果图:
900*100,600*400,400*200,300*200 放入一个1050*1050,margin设置为10,gap设置为8