日撸 Java 三百行（27 天: 汉诺塔问题）
注意：这里是JAVA自学与了解的同步笔记与记录，如有问题欢迎指正说明
目录
一、汉诺塔问题
二、特例枚举从而发现汉诺塔问题的解决思路
三、汉诺塔问题的代码实现
四、数据模拟
总结
一、汉诺塔问题
汉诺塔问题，相信无论是否学习过计算机，也许或多或少都听闻过这个经典的问题。我是在上小学的时候在我爸妈那还只有普通按键的小灵通手机上的只有贪吃蛇还有其他拼图什么游戏当中玩过这个游戏。当年超过四阶就抠脑袋不知道用什么顺序了，当然，现在你说不让我用代码去亲自动手摆数目多的情况我估计也要考虑半天......
（下面我来当历史背景资料的搬运工）汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
说完背景，我们来直接具体描述这个问题：给定三根柱子，记为
、
、
，其中柱子上有
个盘子，从上到下编号为
到
，且上面的盘子一定比下面的盘子小。问：将柱上的盘子经由柱移动到柱最少需要多少次？移动时应注意： ① 一次只能移动一个盘子 ②大的盘子不能压在小盘子上
二、特例枚举从而发现汉诺塔问题的解决思路
解决这种问题要从特例的角度去分析。
如果说 = 1，那么我们的问题就非常简单，因为没有额外更大的盘的限制，我们A柱的盘可以无障碍移动到C，这是一次基本移动就可以完成的。
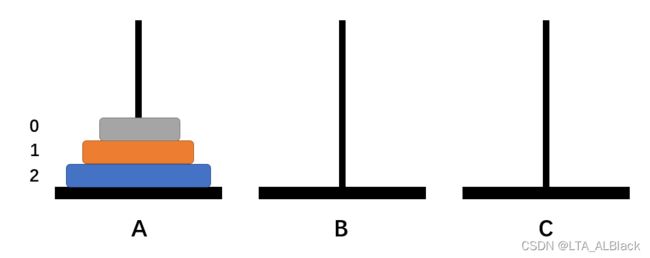
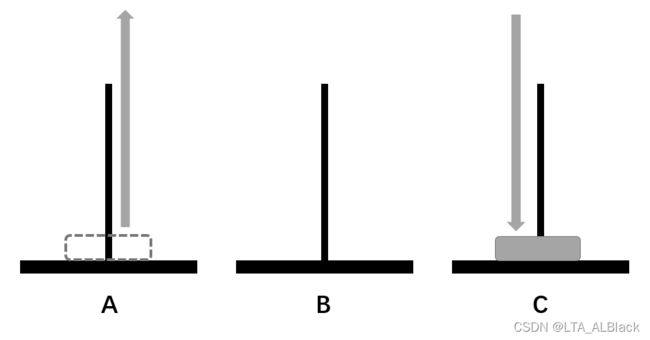
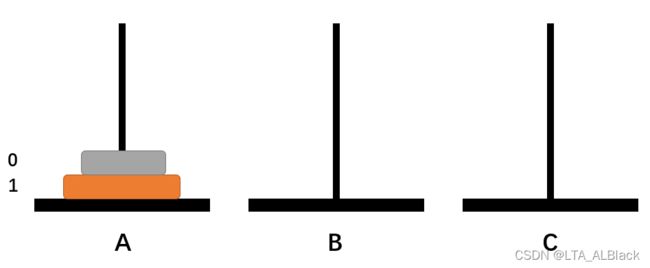
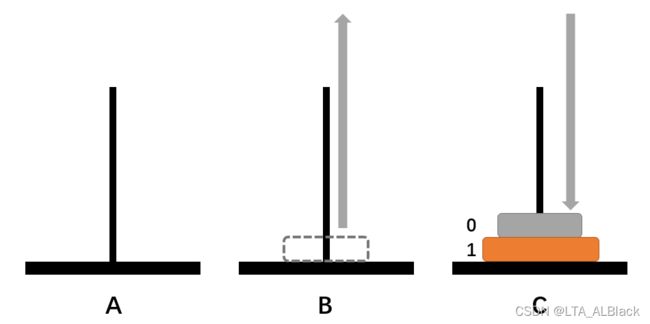
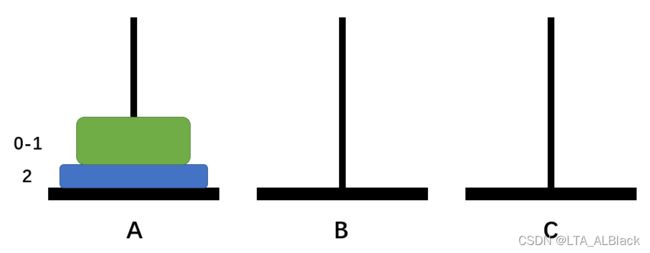
如果说 = 2，那么我们的就需要借助盘B了，因为这时顶端的0号盘并不是在C的底部，只有1号盘属于底部。所以我们需要先将顶端的0号盘暂存于B柱，这时A柱面上的2号盘空余出来了，可以进行转移。按计划转移到C柱，这时B柱上暂时存放的0号盘就有位置可循了，将其挪动到C柱的1号盘之上，最终完成任务。我们这个定义为一次双数目复合移动。
如果说 = 3，那么的思路可以进行一种简化。这种简化非常关键！汉诺塔中的每个盘都有严格的上下级别关系，而每个上侧盘对于每个下侧的盘都表现的是相同的性质：即只要我在你上方，那么后续无论发生什么事我可以放在你上面。于是我们试着把一些上侧的盘全部统一为一个盘。3个盘的案例是利用了这种思想的最简单复合的复合案例，让我们来简单描述下这个过程，这是我们的汉诺塔：
先让我们把第0号、第1号的盘视为一个整体盘，这里我们认为其为【0-1盘】：
然后我们的问题就简化为一个 = 2的汉诺塔问题，这里我们利用刚刚总结的双数目复合移动方案：将【0-1】盘移动到B柱上待机，然后将上部净空后的A上的2盘移动到C柱上，这时再把B柱上待机的【0-1】盘移动到C柱的2盘上（因为之前讲 = 2的移动时用了图全过程说明了这个案例，这里就不再用图进行说明了）
你可能会问，题目不是说一次只能移动一个盘吗？你这【0-1】盘的这么移动不是两个盘吗？其实，我们言语中所谓的“ 【0-1】盘移动到B柱上待机 ”、“ 再把B柱上待机的【0-1】盘移动到C柱的2盘上 ”是一种统一的言论，这里所谓的移动应该翻译为执行一次双数目复合移动方案，这个方案可不是移动一次，其是若干次符合题意的基本移动的若干次组合。要说不同的，就是我们的中间缓存柱可能不一定是B，若我们计划执行一次双数目复合移动方案将复合盘从甲移动到乙，那么中间缓存就是另一个的丙，这个丙视甲乙的不同可以是A、B甚至C。
好勒，我们现在可以进行归纳了，我们似乎可以把任何n个盘的操作转换为前0~n-2个的符合盘与第n-1号盘的双数目复合移动方案。而前面复合盘的操作又可以转换为前0~n-3个的符合盘与第n-2号盘的双数目复合移动方案.......不知道你从上面这个话语中发现了上什么。没错，重复！我们的操作出现了重复，而且相同的操作的重复。在数学上来说，我们发现了的递推，在计算机人眼里，我们发现了递归迭代的过程。
总结：将汉诺塔问题总结为递归问题，单次递归是n=2时的汉诺塔操作，其中递归函数入口是每次对于复合盘的移动操作。
三、汉诺塔问题的代码实现
要想用代码实现汉诺塔问题的话，我们首先需要弄明白的是汉诺塔问题的解是如何表示的。汉诺塔问题步骤上给定了个特殊限制的三个栈，然后考虑如何对第一个栈内元素进行合理转移的过程，这个过程会中途访问另外两个栈。这个过程的描述可以简单描述为一个有向过程
，表示从X号柱移动到Y号柱。
当
，汉诺塔有解的描述：
当
，汉诺塔有解的描述：
当
，汉诺塔有解的描述：![\left [ A\rightarrow C; A\rightarrow B; C\rightarrow B; \right ] A\rightarrow C; \left [ B\rightarrow A; B\rightarrow C; A\rightarrow C \right ]](http://img.e-com-net.com/image/info8/a62ccb2abcf941c0b6a627dfd1d18607.gif){kind=small}
，这个描述中前一段中括号的解释是完成【0-1】复合盘从A移动到B的过程，后端中括号描述的是【0-1】复合盘从B移动到C的过程。
而这每一个中括号就是我们希望实现双数目复合移动方案，若把全局视为两个盘的话也是满足这个方案的。这个方案的移动也似乎有种固定的套路，我们发现无论是n=2还是n=3，中间都是
。这个中间描述刚好就是当前环境下A最底下那个盘移动到C的过程，或者理解为全局来说，我们希望这一堆盘从哪挪到哪。那么缓存柱呢？通过n=2的条件可以发现，缓存柱只参与前半部分和后半部的顶部盘的运转工作，在n=3里面，缓冲柱也加入了前半部分的递归与后半部分的递归中去了。
综上分析，一次汉诺塔移动需要使用源地址，目的地址，中间缓存，当然作为移动重要依据的n也会使用，这样我们便不难设计出如下的递归函数：
/**
*********************
* Move a number of plates
*
* @param paraSource
* The source pole.
* @param paraIntermediary
* The intermediary pole.
* @param paraDestination
* The destination pole
* @param paraNumber
* The number of plates
*********************
*/
public static void hanoi(char paraSource, char paraIntermediary, char paraDestination, int paraNumber) {
if (paraNumber == 1) {
System.out.println(paraSource + "->" + paraDestination + " ");
return;
} // Of if
hanoi(paraSource, paraDestination, paraIntermediary, paraNumber - 1);
System.out.println(paraSource + "->" + paraDestination + " ");
hanoi(paraIntermediary, paraSource, paraDestination, paraNumber - 1);
}// Of hanoi这是一个从paraNumber = n开始，逐步向paraNumber = 1进行递归的过程，当paraNumber == 1时触发特别的递归条件，于是退出函数。我们刚刚提出了递归的目标：将汉诺塔问题总结为递归问题，单次递归是n=2时的汉诺塔操作，其中递归函数入口是每次对于复合盘的移动操作。的再审视这个代码，核心代码的三行抽象化的操作其实就是分别对应具体化的n=2时汉诺塔问题的三步走。
具体的抽象后为描述了源地址柱顶部n-1个盘移动到中转柱的过程：hanoi(paraSource, paraDestination, paraIntermediary, paraNumber - 1);
具体的抽象后为也是一次基本移动，希望这一堆盘从哪挪到哪的操作，将第n个盘（当前函数环境下最大的盘）直接从源柱挪到目标柱。转化为打印语句
具体的
抽象后为描述了中转柱顶部n-1个盘移动到目标柱的过程：hanoi(paraIntermediary, paraSource, paraDestination, paraNumber - 1);
四、数据模拟
下面是完整代码
package datastructure.tree;
/**
* The usage of the if statement.
*
* @author Xingyi Zhang [email protected]
*/
public class Hanoi {
/**
*********************
* Move a number of plates
*
* @param paraSource
* The source pole.
* @param paraIntermediary
* The intermediary pole.
* @param paraDestination
* The destination pole
* @param paraNumber
* The number of plates
*********************
*/
public static void hanoi(char paraSource, char paraIntermediary, char paraDestination, int paraNumber) {
if (paraNumber == 1) {
System.out.println(paraSource + "->" + paraDestination + " ");
return;
} // Of if
System.out.println(paraSource + "->" + paraDestination + " ");
hanoi(paraIntermediary, paraSource, paraDestination, paraNumber - 1);
}// Of hanoi
public static void main(String args[]) {
hanoi('a', 'b', 'c', 3);
}// Of main
}我们只测试下三个盘的情况就好：输出如下（符合预期）
总结
汉诺塔这个游戏让玩家去参与的话，主要难度就是考查每个玩家脑内缓存的信息的存量，当我们决定移动n-1个元素时候，又要先考虑移动这n-1个元素的n-2，n-3......很多玩家操作到中途时就忘了自己在操作第几层的操作了。啊，没错就是我。但是用代码模拟了这个过程后，只需要三行就全部描述完毕，毕竟对于计算机语言来说，这种复杂的递归思想我们交给递归函数来完成，而不用人脑来执行（这个过程用人脑来执行是一种非常痛苦的过程）。
其实汉诺塔的这种缩小操作来设计递归的操作的思想在很多实际的算法中也有体现，比如常见的有分治的思想：“ 分解-解决-合并 ”：将原问题化解为若干个规模小且独立的问题，然后递归地解决他们，最后合并每个解决（汉诺塔的这个合并相对比较弱）。另外的就是树的递归遍历，你看这种两个递归入口中间夹着一个非递归实体操作的递归代码像不像树的中序遍历?所以说汉诺塔的操作某种意义上可以抽象为一种中序的遍历的过程。
汉诺塔的递归解决其实证明了计算机对于某些具有相似性的局部重复性的问题有很好的处理能力，理论上，对于这类问题，只要我们成功归纳出范围缩小的度，我们都能用递归去解决。有时候，可能难不在设计递归，而在于发现这个度，而这个往往需要个人对于问题的理解力。所以，也许走到路的远方才发现：计算机语言不难，难在对于计算机中问题的理解，计算机研究到深处，更多的还是看个人对问题的积累和经验吧。