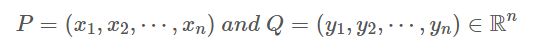python数据分析之KNN（K近邻算法）实践

1、KNN概述

• KNN（K-Nearest Neighbor），即K近邻算法。K近邻就是K个最近的邻居，当需要预测一个未知样本的时候，就由与该样本最接近的K个邻居来决定。
• KNN既可以用于分类问题，也可以用于回归问题。当进行分类预测时，使用K个邻居中，类别数量最多（或加权最多）者，作为预测结果；当进行回归预测时，使用K个邻居的均值（或加权均值），作为预测结果。
• KNN算法的原理在于，样本映射到多维空间时，相似度较高的样本，其距离也会比较接近，反之，相似度较低的样本，其距离也会比较疏远。
• KNN是一种懒惰学习（与急切学习相对应）的算法，它输入基于实例的学习。KNN没有显式的学习过程，也就是说没有训练阶段，数据集事先已有了分类和特征值，待收到新样本后直接进行处理。

2、KNN算法步骤

（1）确定算法超参数

• 确定近邻的数量K
• 确定距离度量方式
• 确定权重计算方式
• 其他超参数

（2）从训练集中选择离待预测样本A最近的K个样本

（3）根据这K个样本预测A

• 对于分类，使用K个样本的类别（或加权类别）预测A。
• 对于回归，使用K个样本目标值（ y ）的均值（或加权均值）预测A。

3、算法超参数

• 超参数，是指我们在训练模型之前，需要人为指定的参数。 该参数不同于模型内部的参数，模型内部的参数是通过训练数据，在训练过程中计算得出的。
• 超参数的不同，可能会对模型的效果产生很大影响。

3.1 K值

• K值（临近数，即在预测目标点时取几个临近的点来预测）的选择，会直接影响到预测结果。
• 当K值较小时，模型会较依赖于附近的邻居样本，具有较好敏感性，但是稳定性会较弱，容易导致过拟合。
• 当K值较大时，稳定性增加，但是敏感性会减弱，容易导致欠拟合。
• 通常情况下，可以通过交叉验证的方式，选择最合适的K值。

3.2 K值的取值方式

• K的取值尽量要取奇数，以保证在计算结果最后会产生一个较多的类别，如果取偶数可能会产生相等的情况，不利于预测。
• 常用的方法是从k=1开始，使用检验集估计分类器的误差率。重复该过程，每次K值增加1，即增加一个近邻，选取产生最小误差率的K。
• 一般k的取值不超过20，上限是n（n为样本总数）的开方，随着数据集的增大，K的值也要增大。

3.3 距离度量方式

• 闵可夫斯基距离（Minkowski distance）：scikit-learn中默认使用的距离度量方式，它是衡量数值点之间距离的一种非常常见的方法。

  假设数值点P和Q坐标如下：

​ 那么，闵可夫斯基距离定义为：

• 曼哈顿距离（Manhattan distance）：当闵可夫斯基距离中的p为1时即为曼哈顿距离，也叫L1距离。
• 欧几里得距离（Euclidean distance）：当闵可夫斯基距离中的p为2时即为欧几里得距离，也叫L2距离。
• 切比雪夫距离（Chebyshev distance）：当闵可夫斯基距离中的p趋近无穷大时即为切比雪夫距离

3.4 权重计算方式

• 统一权重：所有样本的权重相同。
• 距离加权权重：样本的权重与待预测样本的距离成反比，权重之和等于1 。
• 统一权重和距离加权权重算法不一样。
• 距离加权权重分类预测或者回归预测时，都需提前计算权重。

4、KNN算法分类实践

4.1 自定超参数

以鸢尾花数据集为例，使用KNN算法实现分类预测：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

iris = load_iris()
X, y = iris.data[:, :2], iris.target      # 只使用两个特征
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

knn = KNeighborsClassifier(n_neighbors=3, weights="uniform")    # KNN算法，自定k值和权重计算方式
"""
n_neighbors：邻居的数量, 即K值
weights：权重计算方式，可选值为uniform与distance。
		 uniform：统一权重
		 distance：距离加权权重
"""

knn.fit(X_train, y_train)
y_hat = knn.predict(X_test)
print(classification_report(y_test, y_hat))
------------------------------------------------
				precision    recall  f1-score   support

           0       1.00      1.00      1.00        13
           1       0.78      0.44      0.56        16
           2       0.44      0.78      0.56         9

    accuracy                           0.71        38
   macro avg       0.74      0.74      0.71        38
weighted avg       0.77      0.71      0.71        38

不同的超参数值（K值和权重计算方式），会直接影响模型的分类效果：

from matplotlib.colors import ListedColormap
from itertools import product

# 定义决策边界函数，便于可视化
def plot_decision_boundary(model, X, y):
    color = ["r", "g", "b"]
    marker = ["o", "v", "x"]
    class_label = np.unique(y)
    cmap = ListedColormap(color[: len(class_label)])
    x1_min, x2_min = np.min(X, axis=0)
    x1_max, x2_max = np.max(X, axis=0)
    x1 = np.arange(x1_min - 1, x1_max + 1, 0.02)
    x2 = np.arange(x2_min - 1, x2_max + 1, 0.02)
    X1, X2 = np.meshgrid(x1, x2)
    Z = model.predict(np.c_[X1.ravel(), X2.ravel()])
    Z = Z.reshape(X1.shape)
    plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5)
    for i, class_ in enumerate(class_label):
        plt.scatter(x=X[y == class_, 0], y=X[y == class_, 1], 
                c=cmap.colors[i], label=class_, marker=marker[i])
    plt.legend()
    
plt.figure(figsize=(18, 10))
# 使用product计算weights与ks的笛卡尔积组合，这样就可以使用单层循环取代嵌套循环。
weights = ['uniform', 'distance']
ks = [2, 15]
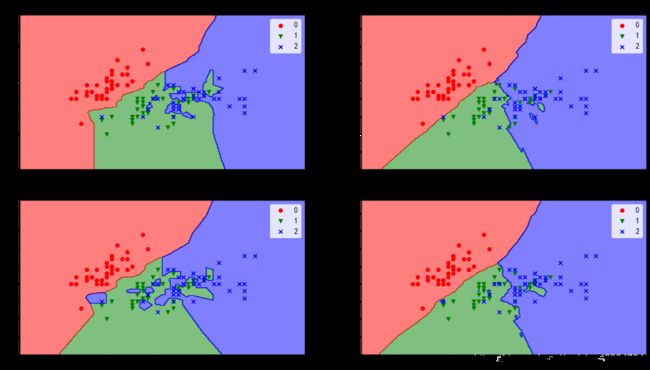
for i, (w, k) in enumerate(product(weights, ks), start=1):
    plt.subplot(2, 2, i)
    plt.title(f"K值：{k} 权重：{w}")
    knn = KNeighborsClassifier(n_neighbors=k, weights=w)  # 不同的超参数分别计算
    knn.fit(X, y)
    plot_decision_boundary(knn, X_train, y_train)

通过上面的结果可以看出：

• K的值越小，模型敏感度越强（稳定性越弱），模型也就越复杂，容易过拟合。
• K的值越大，模型敏感度越弱（稳定性越强），模型也就越简单，容易欠拟合。

4.1 超参数调整

• 在实际应用中，我们很难单凭直觉，就能够找出合适的超参数，通常，我们可以通过网格交叉验证的方式，找出效果最好的超参数。

使用 GridSearchCV 方法找出效果最好的超参数：

from sklearn.model_selection import GridSearchCV

knn = KNeighborsClassifier()
# 定义需要尝试的超参数组合。
grid = {"n_neighbors": range(1, 11, 1), "weights": ['uniform', 'distance']}
gs = GridSearchCV(estimator=knn, param_grid=grid, scoring="accuracy", n_jobs=-1, cv=5, verbose=10, iid=True)
"""
estimator：评估器，即对哪个模型调整超参数。
param_grid：需要检验的超参数组合，从这些组合中，寻找效果最好的超参数组合。
scoring：模型评估标准
n_jobs：并发数量
cv：交叉验证折数
verbose：输出冗余信息，值越大，输出的信息越多。
"""
gs.fit(X_train, y_train)

print(" 最好的分值：", gs.best_score_)
print(" 最好的超参数组合：", gs.best_params_)
print(" 最好的超参数训练好的模型：", gs.best_estimator_)
------------------------------------------------------
最好的分值： 0.8035714285714286
最好的超参数组合： {'n_neighbors': 7, 'weights': 'uniform'}
最好的超参数训练好的模型： KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=7, p=2,
                     weights='uniform')

得到最好的超参数之后，就可以使用最好的超参数训练好后的模型进行预测：

estimator = gs.best_estimator_        # 最好的超参数训练好的模型
y_hat = estimator.predict(X_test)
print(classification_report(y_test, y_hat))
---------------------------------------------
				precision    recall  f1-score   support

           0       1.00      1.00      1.00        13
           1       0.80      0.50      0.62        16
           2       0.47      0.78      0.58         9

    accuracy                           0.74        38
   macro avg       0.76      0.76      0.73        38
weighted avg       0.79      0.74      0.74        38

5、KNN算法回归实践

5.1 常规数据

以波士顿房价数据集为例，使用KNN算法实现回归预测：

from sklearn.datasets import load_boston
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression

X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
"""
没有使用 GridSearchCV 方法找出最佳超参数，因为 gs.fit(X_train, y_train)中 y_train需要为整数，强行将y_train 转为int类型找出的最佳超参数会不准确，此处不适用。
"""
knn.fit(X_train, y_train)

lr = LinearRegression()           # 使用线性回归作为对比
lr.fit(X_train, y_train)

print("KNN算法R^2值：", knn.score(X_test, y_test))
print("线性回归算法R^2值：", lr.score(X_test, y_test))
------------------------------------------------------
KNN算法R^2值： 0.509785478689029
线性回归算法R^2值： 0.6354638433202132

从以上结果可以看出，KNN算法的R²值小于线性回归算法的R²值，效果比线性回归要差很多。但这并不能证明KNN算法是不如线性回归的，这是因为：

• 线性回归在训练参数时，不是基于距离进行计算的，因此，即使线性回归各个特征的量纲（数量级）不同，也不影响最终的拟合效果（权重会不同）。
• KNN是基于距离计算的，如果特征之间的量纲不同，在计算时，量纲较大的特征就会占据主导地位，从而算法会忽略量纲较小的特征，这将会对模型性能造成较大的影响。

5.2 数据标准化

• 数据标准化：在使用算法之前，将数据集中的特征转换成相同的量纲，从而消除不同量纲对算法造成的负面影响，我们将这个过程称为数据标准化。
• 实际上，即使特征量纲相同，标准化也不会产生负面影响。
• 在scikit-learn中，常用的标准化方式为均值标准差标准化（StandardScaler）与最小最大值标准化（MinMaxScaler）。

使用 StandardScaler 进行均值标准差标准化：

from sklearn.preprocessing import StandardScaler

s = StandardScaler()
X_train_scale = s.fit_transform(X_train)
X_test_scale = s.transform(X_test)
knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
knn.fit(X_train_scale, y_train)
print("均值标准差标准化之后的KNN算法R^2值：", knn.score(X_test_scale, y_test))
-------------------------------------------
均值标准差标准化之后的KNN算法R^2值： 0.6248800677762865

使用 MinMaxScaler 进行最小最大值标准化：

from sklearn.preprocessing import MinMaxScaler

s = MinMaxScaler()
X_train_scale = s.fit_transform(X_train)
X_test_scale = s.transform(X_test)
knn = KNeighborsRegressor(n_neighbors=3, weights="uniform")
knn.fit(X_train_scale, y_train)
print("最小最大值标准化之后的KNN算法R^2值：", knn.score(X_test_scale, y_test))
---------------------------------------
最小最大值标准化之后的KNN算法R^2值： 0.6177749492293981

从以上结果可以看出，进行数据标准化处理之后，KNN算法效果有了进一步提升。

5.3 流水线优化

• 流水线（Pipeline类）可以将每个评估器视为一个步骤，然后将多个步骤作为一个整体而依次执行，这样，我们就无需分别执行每个步骤。
• 流水线具有最后一个评估器的所有方法， 当通过流水线对象调用方法 f 时，会执行这样的过程（假设流水线具有个评估器）：如果 f 是fit方法，则会首先对前n - 1个评估器依次调用fit_transform方法，然后在最后一个评估器上调用 f(fit）方法；如果 f 是其他方法，则会首先对前 n - 1个评估器依次调用transform方法，然后在最后一个评估器上调用 f 方法。

使用 Pipeline 把上面的均值标准差标准化与训练模型两个步骤视为一个整体，一并执行：

from sklearn.pipeline import Pipeline

X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

steps = [("scaler", StandardScaler()), ("knn", KNeighborsRegressor())]
"""
定义流水线的步骤，类型为一个列表，列表中的每个元素是元组类型。
格式为：[(步骤名1，评估器1), (步骤名2， 评估器2)，……， (步骤名n, 评估器n)]
"""
p = Pipeline(steps)
p.set_params(knn__n_neighbors=3, knn__weights="uniform")   # 设置流水线的参数。
p.fit(X_train, y_train)
------------------------------------
print("流水线之后的R^2值：", p.score(X_test, y_test))
-------------------------------------------
流水线之后的KNN算法R^2值： 0.6248800677762865

拓展：KD树

• 当样本数量较少时，我们可以使用遍历所有样本的方式，找出最近的K个邻居，然而，如果数据集庞大，这种方式会造成大量的时间开销，此时，我们可以使用KD树的方式来选择K个邻居。
• KD树算法中，首先是对训练数据进行建模，构建KD树，然后再根据建好的模型来获取邻近样本数据。