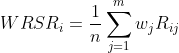综合评价法——秩和比(RSR)
一、背景介绍
秩和比法,是我国统计学家田凤调教授于1988年提出的一种综合评价方法,是利用秩和比(RSR, Rank-sum ratio)进行统计分析的一种方法。它不仅适用于四格表资料的综合评价,也适用于n行m列资料的综合评价,同时也适用于计量资料和分类资料的综合评价。
该方法在医疗卫生、科技、经济等领域的多指标综合评价、统计预测预报、统计质量控制、鉴别分类等方面已得到广泛的应用。
二、原理及优缺点
原理:秩和比综合评价法基本原理是在一个n行m列,通过秩的转换,获得无量纲统计量RSR;然后运用参数统计分析的概念与方法、研究RSR的分布;以RSR值对评价对象的优劣进行分档排序,从而对评价对象做出综合评价。
优点:是非参数统计分析,对指标的选择无特殊要求,适于各种评价对象;由于计算用的数值是秩次,可以消除异常值的干扰,它融合了参数分析的方法,结果比单纯采用非参数法更为精确,既可以直接排序,又可以分档排序,使用范围广泛。
缺点:是排序的主要依据是利用原始数据的秩次,最终算得的RSR值反映的是综合秩次的差距,而与原始数据的顺位间的差距程度大小无关,这样在指标转化为秩次是会失去一些原始数据的信息,如原始数据的大小差别等。
当RSR值实际说不满足正态分布时,分档归类的结果与实际情况会有偏差,且只能回答分级程度是否有差别,不能进一步回答具体的差别情况。
三、算法步骤
设
![]()
是从一元总体抽取的容量为n的样本,并按从小到大的顺序排列,设其统计量为
![]()
若
![]()
,则称k是xi在样本中的秩,记作Ri,对每一个i=1,2,...,n,称Ri是第i个秩统计量。R1,R2,...,Rn总称为秩统计量。
3.1编秩
编秩方法有整次秩和比法和非整次秩和比法。二者在于计算秩的时候公式不一样。一般使用整次和比法。
3.1.1整次秩和比法
设有n个评价对象,m个评价指标的样本数据(n行m列),分别对每个指标列的数据编秩:正向指标(值越大越好)从小到大编秩,负向指标(值越小越好)从大到小编秩,当数据的值相同时编平均秩。得到秩矩阵R=(Rij)n×m。
注:编秩即对数据排序,其顺序号作为秩。
如下表:
对X3,按从小到大排序,其中值为75的有两个指标,按算术平均进行编秩:(2+3)/2=2.5
| 语文(X1) | R1 | 数学(X2) | R2 | 英语(X3) | R3 | |
| 甲 | 66 | 1 | 80 | 4 | 70 | 1 |
| 乙 | 85 | 4 | 75 | 3 | 75 | 2.5 |
| 丙 | 79 | 2 | 62 | 1 | 85 | 4 |
| 丁 | 84 | 3 | 93 | 5 | 90 | 5 |
| 戊 | 87 | 5 | 77 | 2 | 75 | 2.5 |
3.1.2非整次秩和比法
用类似于线性插值的方式对指标值进行编秩,以改进RSR法编秩方法的不足,所以编秩次与原指标值之间存在定量的线性对应关系。
对于正向指标:
对于负向指标:
3.2计算SRS、WRSR
在一个 n 行( n 个评价对象)m 列( m个评价指标)矩阵中,RSR的计算公式为:
上式中,![]() ,
,![]() 表示第 i 行 第 j 列元素的秩。
表示第 i 行 第 j 列元素的秩。
当个评价指标的权重不同时,计算加权秩和比为WRSR,其计算公式为:
3.3计算概率单位
按小到大的顺序编制RSR或者WRSR频率分布表,列出各组频数fi,计算各组累计频数Fi,计算累计频率pi=Fi/n,将pi转换为概率单位probiti。
3.4计算回归方程
以累计频率所对应的概率单位值 Probit 为自变量,以RSRi或者WRSRi值为因变量,计算回归方程:
![]()
可利用最小二乘法求出相当应参数。
3.5分档排序
按回归方程计算的RSR/WRSR估计值,对评价对象进行分档排序。分档数由研究者根据实际情况决定。一般档次数量为 3档 ,也可以是 4挡、5挡。
四、案例
以基金投资案例说明,选取5个指标对基金投资进行评价。
其中X1,X2,X3为正向指标(效益型指标),值越大越好,排序时从小到大排。
X4,X5为负向指标(成本型指标),值越低越好,排序时从大到小排。
| x1 | x2 | x3 | x4 | x5 | |
| 1 | 34100 | 0.999091 | 0.98 | 0.971793 | 0.002727 |
| 2 | 22630 | 0.673973 | 0.673973 | 1 | 0 |
| 3 | 5766 | 0.774194 | 0.774194 | 0.993056 | 0 |
| 4 | 34565 | 0.910314 | 0.896861 | 0.796059 | 0.006278 |
| 5 | 13206 | 0.680751 | 0.664319 | 0.772586 | 0.00939 |
| 6 | 34100 | 0.831567 | 0.804476 | 0.805949 | 0.014134 |
| 7 | 45200 | 0.836852 | 0.807654 | 0.899654 | 0.000912 |
| 8 | 79560 | 1 | 0.9365 | 0.99352 | 0.2187 |
程序如下所示:
clc,clear
a=load('shuju.txt');%该数据横向是指标,纵向是指标每年的数据
w=[0.2 0.3 0.2 0.2 0.1];%假设求得的权重
a(:,[3,5])=-a(:,[3,5]);
%这里的3,4,5指标为负向指标,也就是指标值越小越好,为与正向指标同步,因此这里乘以个负号
ra=tiedrank(a);
%[R, tie] = tie(X)计算向量X中值的秩,如果有任何X值被束缚,tie计算它们的平均秩。
%返回值是对非参数测试信号秩和ranksum所要求的关系的调整,以及对Spearman秩相关的计算。
%例子:从最小到最大,两个20的值是2和3,所以它们都是2。5(平均2和3):
%tiedrank([10 20 30 40 20])
%ans =1.0000 2.5000 4.0000 5.0000 2.5000
[n,m]=size(ra);%求矩阵维度
RSR=mean(ra,2)/n;
%mean求数组的平均数或者均值
%mean(A,2)返回值为该矩阵的各行向量的均值(每行的平均值)
W=repmat(w,[n,1]);%用于复制平铺矩阵,相当于讲w矩阵看成一个元素,形成n×1维的矩阵并用W矩阵记录
WRSR=sum(ra.*W,2)/n;
[sWRSR,ind]=sort(WRSR);%sort为排序函数
p=[1:n]/n;
p(end)=0.99999;
%p(end)=1-1/(4*n);
Probit=norminv(p,0,1);
%norminv函数,正态分布概率值, X = NORMINV(P,A,S) ,其中,P取概率。A取均值。S取方差。
%然后返回值X就是指满足均值为A,方差为S的高斯分布的累计概率密度值。即F(a)=P,返回值就是a。
%至于F的含义:对连续函数,所有小于等于a的值,其出现概率的和为F(a)=P(x结果:
| 5 | 0.4669 | 8 |
| 6 | 0.4939 | 7 |
| 3 | 0.5141 | 6 |
| 4 | 0.5322 | 5 |
| 2 | 0.5503 | 4 |
| 1 | 0.5705 | 3 |
| 7 | 0.5976 | 2 |
| 8 | 0.7744 | 1 |