使用线性SVM支持向量机简单分类数据

支持向量机简单来说就是与分类器平行的两个平面，此两个平面能够很好的分开两类数据，且穿越穿越两类数据集中的点，我们寻求最佳超几何平面使之与两个平面的距离最大，如此实现分类总误差的距离最小。
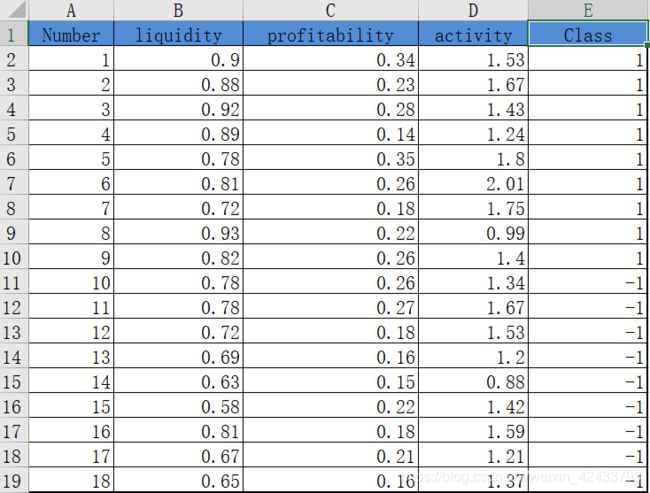
通过下面数据建立一种规则来决定是否批准贷款，1表示批准，-1表示不批准。

matlab代码为：

clc
clear
X0=xlsread('SVM_ex2','B2:E19');
for i=1:3
    X(:,i)=(X0(:,i)-mean(X0(:,i)))/std(X0(:,i));%数据标准化
end
%%数据预处理
[m,n]=size(X);
e=ones(m,1);
D=[X0(:,4)];%%%代表各个企业的类别
B=zeros(m,m);
C=zeros(m,m);
for i=1:m
    B(i,i)=1;
    C(i,i)=D(i,1);
end
%%转化为规划模型求解
A=[-X(:,1).*D,-X(:,2).*D,-X(:,3).*D,D,-B];
b=-e;
f=[0,0,0,0,ones(1,m)]';
lb=[-inf,-inf,-inf,-inf,zeros(1,m)]';
x=linprog(f,A,b,A,b,lb)
%%模型验证与结果显示
W=[x(1,1),x(2,1),x(3,1)];
CC=x(4,1);
X1=[X(:,1),X(:,2),X(:,3)];
R1=X1*W'-CC;
R2=sign(R1);%进行分类
disp('程序输出结果为:');
disp('超平面方程为：');
disp(['X1:' num2str(x(1,1))]);%%%%%中间要空一格。
disp(['X2:' num2str(x(2,1))]);
disp(['X3:' num2str(x(3,1))]);
disp(['intercept:' num2str(x(4,1))]);
disp('超平面分类结果为：')
R=[R1,R2]

运行结果为：

程序输出结果为:
超平面方程为：
X1:0.59428
X2:0.079851
X3:0.10123
intercept:-0.11953%%常量
超平面分类结果为：

R =

    1.0000    1.0000
    0.7951    1.0000
    1.0000    1.0000
    0.5827    1.0000
    0.4316    1.0000
    0.5596    1.0000
   -0.1440   -1.0000
    0.8227    1.0000
    0.3991    1.0000
    0.1520    1.0000
    0.2822    1.0000
   -0.2222   -1.0000
   -0.5347   -1.0000
   -1.0000   -1.0000
   -1.0000   -1.0000
    0.3071    1.0000
   -0.5796   -1.0000
   -0.7000   -1.0000

从分类结果上，线性分类模型存在一定误差，但这种误差是可以接受的。如果应用非线性SVM，分类结果正确率可以达到100%，但非线性的推广能力较差，对于新模型来说，非线性SVM的结果可能还没有线性模型的好，且线性SVM的解释性更好，所以选择线性SVM。