随机信号分析实验（matlab仿真实验）

一.实验内容：

(1) 产生均匀分布的随机数，高斯分布的随机数和其他分布（瑞利，卡方）的随机数及画图，对生成的随机数进行分析；
(2) 检验（1）中产生的均匀分布，高斯分布的数学期望和方差，并画出各种分布的随机变量的概率密度直方图；
(3) 两组及多组独立的均匀分布的随机数做和统计和的概率密度直方图；
(4) 用一个数学期望为0和不为0，方差为某值的高斯分布随机数，作为样本序列求自相关函数的估值，并用图形表示；
（5）并计算出的自相关函数的估值，作为样本序列求功率谱密度的估值，并用图形显示；
（6）仿真信号加白噪声经过系统前后的自相关函数和功率谱密度并图示；

二.实验原理：

实验一 各种分布随机数的产生

（一） 实验原理

1. 均匀分布随机数的产生原理
产生伪随机数的一种实用方法是同余法，它利用同余运算递推产生伪随机数序列，最简单的方法就是加同余法

为了保证产生的伪随机数能在【0，1】上均匀分布，需要M为正整数，此外常数c和初值y0亦为正整数。加同余法虽然简单，但产生的伪随机数效果不好，另一种同余方法为乘同余法，它需要两次乘法才能产生一个在【0，1】上均匀分布的随机数，

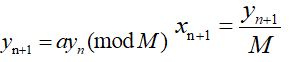
Matlab给我们提供了random函数供我们产生满足条件的均匀分布随机数，
a. Rand()函数：产生均匀分布随机数
b. Rand(M,N)函数：产生M行N列均匀分布的随机数；
c. X=random(‘unif’,a,b,N,M)函数：产生m行n列在a到b上随机分布的随机数；
2. 高斯分布随机数的产生原理
由于高斯随机变量的重要性，很有必要讨论一下高斯随机数的产生，广泛应用的有两种产生高斯分布随机数的方法，一种是变换法，一种是近似法。
（1） 变换法：
如果X1和X2是两个相互独立的均匀分布的随机数，那么下面两式：

（2） 近似法： 便是数学期望为m，方差为δ的平方的高斯分布随机数，且相互独立，这就是变换法
首先考虑获得数学期望为0，方差为1的高斯分布随机数，由于在【0，1】区间上均匀分布的随机变量X的
数学期望为

方差为

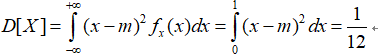
而如果有若干个不同的X相加构成新的随机变量 ，

那么当n足够大时随机变量Y是数学期望为0，方差为1的高斯分布随机数做变换 ，

即可产生符合要求的高斯分布随机数。
在学习中心极限定理时，曾提到n个在[0,1]区间上均匀分布的互相独立随机变量Xi (i=1,2…,n)，当n足够大时，其和的分布接近高斯分布。当然，只要n不是无穷大，这个高斯分布是近似的。由于近似法避免了开方和三角函数运算，计算量大大降低。当精度要求不太高时，近似法还是具有很大应用价值的。

3. 由高斯分布产生其他分布的随机数
有了高斯随机变量的仿真方法，就可以构成与高斯变量有关的其他分布随机变量，如瑞利分布、指数分布和 分布随机变量。
（1） 基于数学期望为0的高斯变量变换产生的随机变量分布
a. 瑞利分布

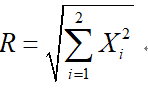
b. 广义瑞利分布

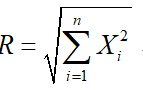
c. 指数分布

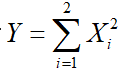
d. 中心卡方分布

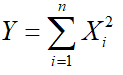
（2） 基于数学期望不为0的高斯变量变换产生随机变量分布
a. 非中心卡方 分布；

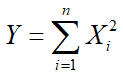
b. 莱斯分布：

4. 对生成的随机数进行分析
在实际应用之中，产生随机数之后，必须对它的统计特性做严格的检验，一般来讲，统计特性的检验包括参数检验，均匀性检验和独立性检验。事实上，如果在二阶范围内讨论随机信号，那么参数检验只能对产生的随机数的一，二阶矩进行检验。此外，参数检验还应该包括最小值，最大值，周期等。
5. 随机变量函数变换
根据随机变量函数变换的原理，如果能将两个分布之间的函数关系用显式表达，那么就可以对一种分布的随机变量进行变换得到另一种分布的随机变量。

实验二 随机变量的检验

1. 随机变量数字特征的验证：
产生的随机数可以作为一个随机变量，也可以作为一个随机过程之中的样本函数，不论是随机变量还是随机过程的样本函数，都会遇到求其数学特征的情况，在图像处理时，也时常需要计算图像灰度直方图的数学期望，方差，峰态和偏态系数等等，事实上，在很多情况下，无法得到或者不能利用随机变量的全部样本，只能利用一部分样本来获得随机变量数字特征的估计值，估计值应该依概率收敛于被估计的参数；
随机数产生之后，必须对它的统计特性做严格的检验。一般来讲，统计特性的检验包括参数检验、均匀性检验和独立性检验等。事实上，我们如果在二阶矩范围内讨论随机信号，那么参数检验只对产生的随机数一、二阶矩进行检验。我们可以把产生的随机数序列作为一个随机变量，也可以看成随机过程中的一个样本函数。不论是随机变量还是随机过程的样本函数，都会遇到求其数字特征的情况，有时需要计算随机变量的概率密度直方图等。

（1） 均值的检验：
设随机数序列为
a. 一种计算均值的方法就是直接计算下式
，式中xn为随机数序列的第n个随机数；
b. 另一种计算方法是利用递推算法，第n次迭代的均值即前n个随机数的均值为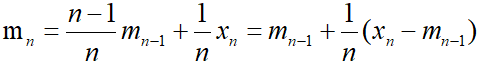 迭代结束之后，便可以得到随机数序列的均值 ，递推算法的优点在于可以实时计算均值，这种方法常用于在实时获取数据的场合；
d. 当数据量较大时，为了防止误差的积累，也可以采用 ,m1是取一小部分随机数计算的均值
（2） 方差的检验：
计算方差也可以用直接法和递推法，仿照均值的做法

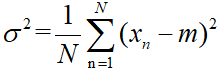
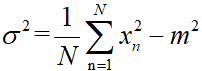两种计算方式有利有害，前者计算误差更小，但是后者可以节省运算次数。
方差的递推算法需要同时递推均值和方差：


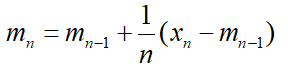
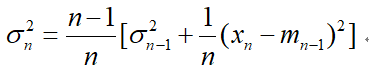
2. 多组相互独立均匀分布随机数做和
如果n个独立的随机变量的分布是相同的，并且具有有限的数学期望和方差，当n趋向于无穷大时，它们之和趋向于高斯分布。这就是中心极限定理中的一个定理，它说明了如果每一个随机变量对和的贡献相同，则在一定条件下，其和是高斯分布的。
中心极限定理还指出：即使n个相互独立的随机变量不是相同分布的，当n无穷大时，如果满足任何一个随机变量都不占优或者对和的影响足够小，那么它们之和仍然会趋向于高斯分布。
利用计算机产生均匀分布的随机数。对相互独立的均匀分布的随机变量做和，可以很直观看到均匀分布的随机变量的和，随着做和次数的增加分布情况的变化，通过实验对中心极限定理的进行验证。

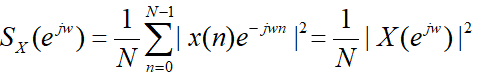
3. 统计随机数的概率密度直方图
假定被统计的序列x(n)的最大值和最小值分别为a和b。将 (a,b)区间等分M（M应与被统计的序列 x(n)的个数N相适应，否则统计效果不好。）份后的区间为 ， ，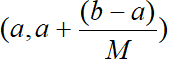

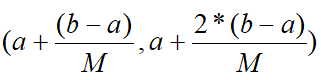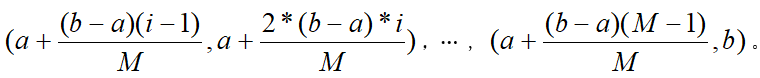
实验三 自相关函数，功率谱密度估计

1. 自相关函数的估计
在信号处理之中，经常需要估计自相关函数，学会怎样处理自相关函数是很重要的；
1. 直接估计法
如果随机序列为各态历经序列，由于其自相关函数具有各态历经性，可以用自相关函数来估计。若各态历经序列Xn的一个样本有N个数据，用直接估计法获得的自相关函数为 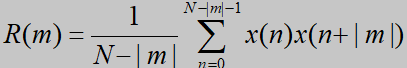一般情况下，N比较大，为了方便，时间自相关函数经常由下式估计
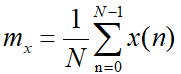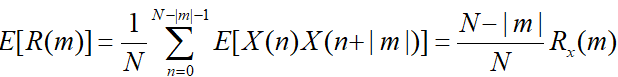除了自相关函数外 ，有时候还需要估计序列的均值和方差。在假设序列Xn满足各态历经性的前提下，Xn的均值可以用一个样本去估计 方差的估计值是 对所有样本的自相关估计值求数学期望， matlab函数中的xcorr函数可以很方便的计算出随机序列的自相关和互相关序列。
2. 通过FFT估计自相关函数
虽然相关函数和线性卷积的物理意义不同，但是两者却有相似的计算形式，都包括移位，相乘和求和，差别仅在于线性卷积多了一个序列的翻转。 自相关函数可以有以下两式完成，

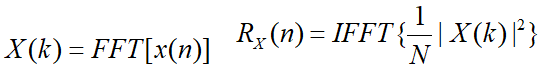
2. 功率谱函数的估计、
由于随机信号是不满足绝对可积的条件的，因此是不存在频谱的，但是工程之中常用到的是功率型信号，可以用功率谱密度来描述其频域特性
一般把平稳随机序列的功率谱定义为自相关序列的傅里叶变换。如果自相关序列是周期序列，可仿照随机过程的情况，引人适当的函数。平稳序列X(n)的功率谱与自相关序列的关系为

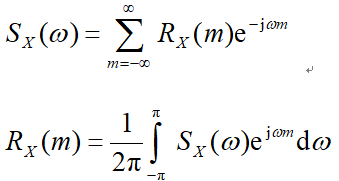
与实平稳过程一样，实平稳序列的功率谱也是非负偶函数，即

可以证明，功率谱还可表示为:

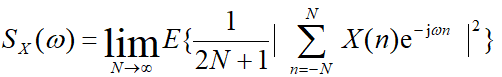
1. 直接法（周期图法）
一般情况下，随机序列Xn的某个样本xn的观测序列长度是有限的，若序列长度为N，则可以认为是一个能量有限的序列，若xn的离散时间傅立叶变换存在，则

2. 间接法（自相关函数法）
由维纳—欣钦定理可知，功率谱密度和相关函数是一对傅里叶变换对，因此先用序列xn估计出自相关函数r,然后对r进行傅里叶变换，就可以得到功率谱密度的估计值

实验四 随机信号通过系统前后信号仿真

需要先仿真一个指定系统，再根据需要仿真输入的随机信号，然后使这个随机信号通过指定的系统。通过对实际系统建模, 计算机可以对很多系统进行仿真。在信号处理中，一般将线性系统分解为一个全通放大器（或衰减器）和一个特定频率响应的滤波器。由于全通放大器可以用一个常数代替，因此线性系统的仿真往往只需设计一个数字滤波器。滤波器设计可采用MATLAB提供的函数，也可利用相应的方法自行设计。MATLAB提供了多个设计滤波器的函数，可以很方便地设计低通、带通、高通、多带通、带阻滤波器。

（二） 所用到的MATLAB函数

（1） Rand()函数；rand(M,N)函数；
（2） Random(‘unif’,a,b,N,M):用于生成M行N列在a~b上均匀分布的随机数；
Random(‘normal’,m,v,M,N):用于产生M行N列高斯分布随机数
（3） 自定义函数：y=easyGaussRandomNumbers_2(N,Mean,Variance)
（4） subplot(m,n,p)此 MATLAB 函数 将当前图形划分为 m×n 网格，并在 p 指定的位置创坐标轴。按行号对子图位置进行编号。第一个子图是第一行的第一列，第二个子图是第一行的第二列，依此类推。如果指定的位置已存在坐标轴，则此命令会将该坐标轴设为当前坐标轴。
（5） plot(X,Y) plot - 二维线图 此 MATLAB 函数 创建 Y 中数据对 X 中对应值的二维线图。 如果 X 和 Y 都是矢量，则它们的长度必须相同。plot 函数绘制 Y 与 X的相对图。 如果 X 和 Y 均为矩阵，则它们的大小必须相同。plot 函数绘制 Y 的列对 X 的列的图。 如果 X 或 Y中的一个是矢量而另一个是矩阵，则矩阵的各维中必须有一维与矢量的长度相等。如果矩阵的行数等于矢量长度，则 plot 函数绘制矩阵中的每一列对矢量的图。
（6） Rx=xcorr(xn,‘biased’) 用于求自相关函数；
（7） Y = fft(X)， Y = fft(X,n)，Y = fft(X,n,dim)快速傅里叶变换
（8） h=fir1(100,0.6,‘high’);%设计一个高通滤波器，阶数为100，截止频率为0.6

(三)实验结果

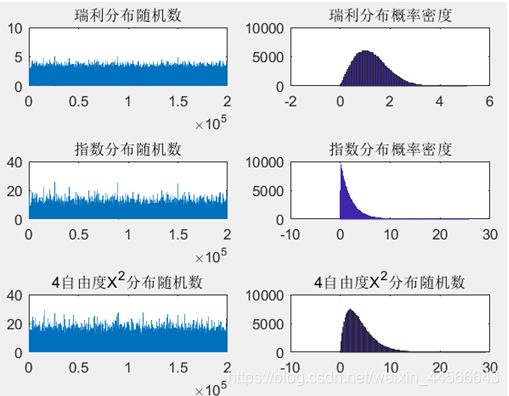
（一） 实验一 各种分布随机数的产生

（1） 三种不同方法产生均匀分布的随机数

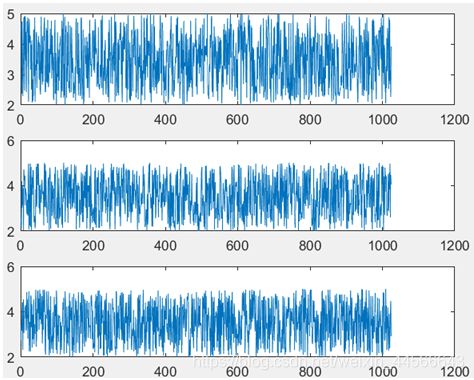
发现产生的效果都是相同的
（2） 均值为0的高斯分布产生不同分布的随机数：产生瑞利分布，指数分布，4自由度X^2分布的随机数,并观察其概率密度

由均值为0的高斯分布产生瑞利分布和卡方分布的随机数

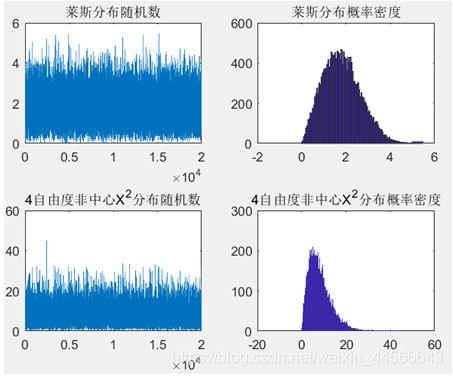
（3） 均值不为0的高斯分布产生不同分布的随机数：生成非中心卡方分布和莱斯分布随机数

（4） 不同方法得到的高斯分布随机数

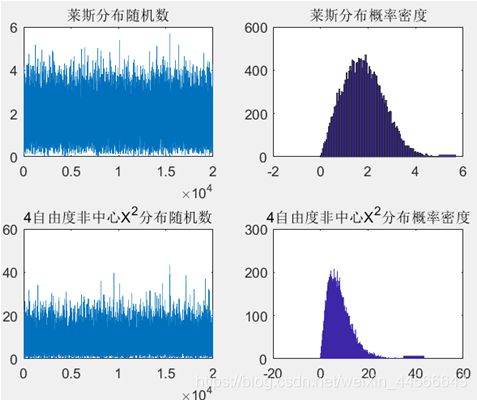
（二） 实验二 随机变量的检验

（1） 均值的检验
a. 检验均匀分布均值（产生2到5上均匀分布的随机数）

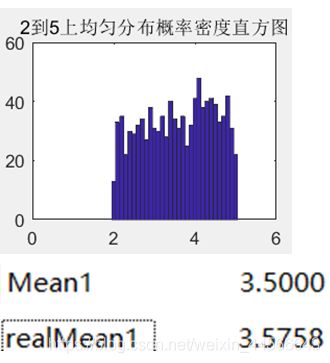
理论上均值为3.5，实际算出的均值为3.55758

b. 高斯分布的均值，产生的是均值为0，方差为1的随机数

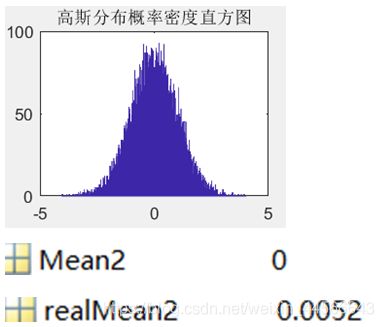
理论上的均值为0，实测的均值为0.0052，相差微乎其微
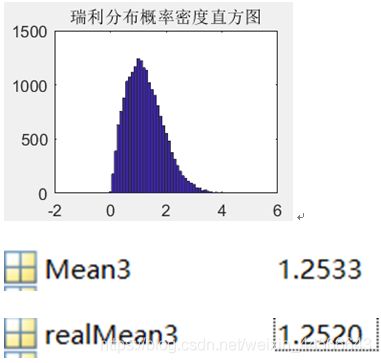
c. 瑞利分布的均值

理论上均值为1.2533，实测的均值为1.2520，相差微乎其微
d. 卡方分布

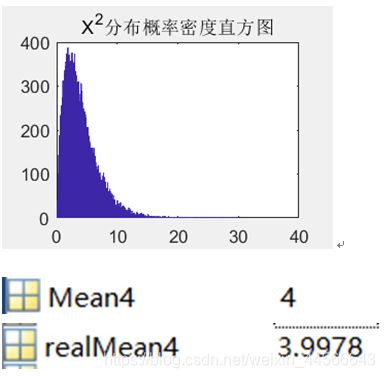
理论上均值为4，实测的均值为3.9978，相差微乎其微

（2） 方差的检验
a. 均匀分布的方差

b. 高斯分布的方差

c. 瑞利分布的方差

d. 卡方分布的方差

e. 综述：

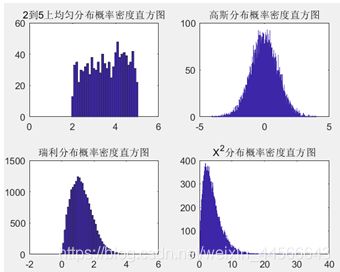
（3） 多组相互独立均匀分布随机数做和

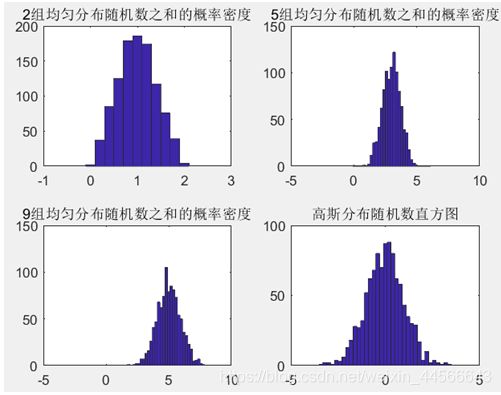
如果n个独立的随机变量的分布是相同的，并且具有有限的数学期望和方差，当n趋向于无穷大时，它们之和趋向于高斯分布。这就是中心极限定理中的一个定理，它说明了如果每一个随机变量对和的贡献相同，则在一定条件下，其和是高斯分布的。

（4） 多组相互独立均值为0高斯分布随机数做和

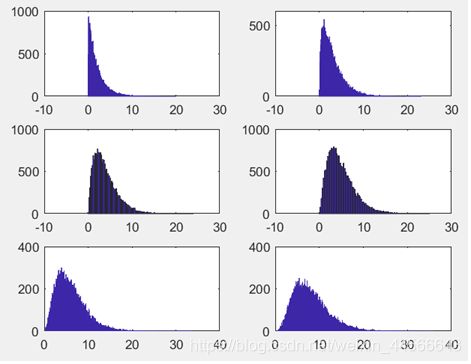
（5） 不同自由度下的瑞利分布对比

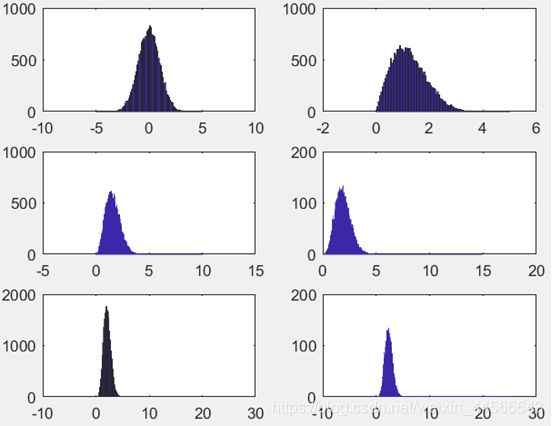
（6） 不同自由度下的卡方分布概率密度

（7） 多组相互独立均值不为0的高斯分布随机数做和

（三） 实验三 自相关函数，功率谱密度估计

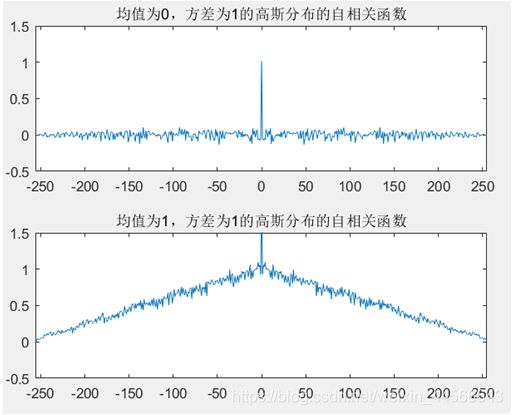
（1） 自相关函数
a. 均值为0，方差为1的高斯分布的自相关函数

b. 均值为1，方差为1的高斯分布的自相关函数

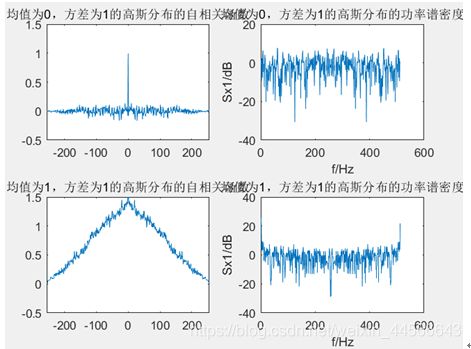
（2） 功率谱密度
a. 均值为0，方差为1的高斯分布的功率谱密度
b. 均值为1，方差为1的高斯分布的功率谱密度

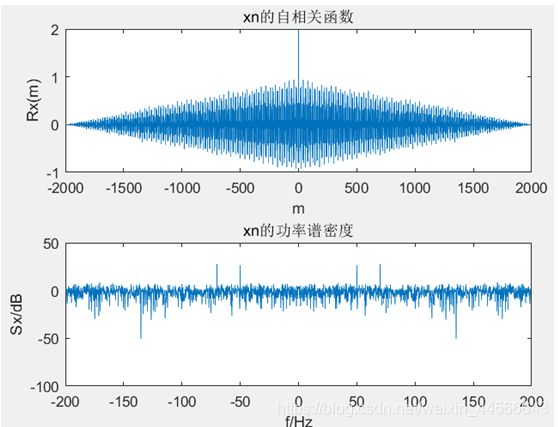
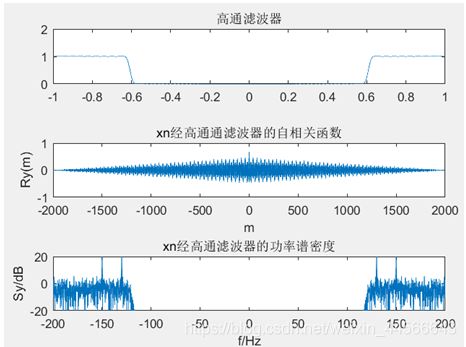
（四） 实验四 随机信号通过系统前后信号仿真

（一）设计信号加噪声通过高通滤波器
a. 信号本身：

b. 信号加噪声通过系统之后：

（三） 设计信号加噪声通过低通滤波器：
（1）信号通过系统前：

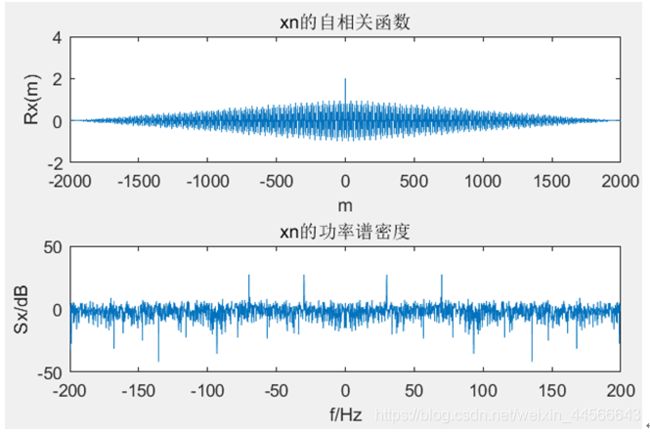
（3） 信号加噪声通过系统之后

三． 个人感想与总结

在本次实验之中，
（1） 首先学习了各种分布的随机数如何产生，编写三种不同的方法来产生均匀分布的随机数，同时也编写了自定义函数用于产生高斯分布随机数，同时可以产生高斯分布随机数的方法还有直接法和近似法，都很有效，
（2） 之后我验证了不同种类随机变量之间相互转换的可能性，
（3） 同时也验证了高斯分布，瑞利分布，卡方分布，等分布的均值和方差，发现确实与理论值相差很小，
（4） 之后画出来了各种分布的概率密度直方图，让我对各种分布有了一个更直观的感知，
（5） 之后我用均值为0，和均值不为0的高斯分布随机数产生了瑞利分布，指数分布，卡方分布，莱斯分布，非中心卡方分布，广义瑞利分布等分布，对高斯分布的灵活性和重要性有了更加深入的认知；
（6） 接着我研究了卡方分布和瑞利分布随着自由度的增加其对概率密度的影响，带给了我很直观的感受。
（7） 然后我研究了两组及两组以上均匀分布随机数做和，验证了中心极限定理，受益匪浅。
（8） 之后为了对随机信号有更加深入的认识，我又研究了数学期望为0和数学期望不为0的高斯分布的随机数作为样本序列来对自相关函数和功率谱密度进行估值，并用图形化显示，对于信号的时域和频域及其联系都有了更加深入的认识。
（9） 最后我设计了高通滤波器和低通滤波器，分别让信号和高斯白噪声通过，研究其通过系统前后的自相关函数和功率谱密度的变化，对于滤波器的特性有了更加深入的了解。
（10） 最后通过本次实验，让我对MATLAB使用的更加顺手，对各种分布的认识又上了一个台阶，同时对于信号与系统的理解更加深入，总之一句话，这次试验我受益匪浅。

四． 附录：程序代码

%本脚本用于编写1024个在区间2~5上均匀分布的随机数的程序
for n=1:1024
y1=rand();
x1(n)=y1*(5-2)+2;
end
subplot(311);plot(x1);
y2=rand(1,1024);
x2=3y2+2;
subplot(312);plot(x2);
x3=random(‘unif’,2,5,1,1024);subplot(313);plot(x3);
%例1.6.3.本实验用于产生两个相互独立的高斯随机变量，
function [xr,xi]=GaussRandNumb_1(N,Mean,Variance)
for n=1:N
a=sqrt(-2.0log(rand()));
b=2pirand();
xr(n)=Varianceacos(b)+Mean;
xi(n)=Varianceasin(b)+Mean;
end
%下面写的是调用函数的示例，
%[x1,x2]=GaussRandNumb_1(1024,0,1);
%subplot(211);plot(x1,‘k’);
%subplot(212);plot(x2,‘r’);

%这个是课本上例1.6.4第一个产生高斯分布随机数的方法，其调用方法为y=GaussRandomnumber_2(1024,0.5,2)就可以产生1024个数学期望为0.5方差为2的高斯随机数
function y=GaussRandomnumber_2(N,Mean,Variance)
for j=1:N
y(j)=0.0;
for k=1:12
x(k)=rand();
y(j)=y(j)+x(k);
end
end
for j=1:N
y(j)=Variance*(y(j)-6)+Mean;
end
subplot(211);plot(x);
subplot(212);plot(y);
%本脚本用于生成非中心卡方分布和莱斯分布随机数，观察其概率密度
N=20000;
G1=random(‘Normal’,1,1,1,N);
G2=random(‘Normal’,1,1,1,N);
G3=random(‘Normal’,1,1,1,N);
G4=random(‘Normal’,1,1,1,N);
L=sqrt(G1.*G1+G2.*G2);
E=G1.*G1+G2.*G2;
X2=G1.*G1+G2.*G2+G3.*G3+G4.*G4;
subplot(221);plot(L);title(‘莱斯分布随机数’);
subplot(222);hist(L,0:0.05:5);title(‘莱斯分布概率密度’);
subplot(223);plot(X2);title(‘4自由度非中心X^2分布随机数’);
subplot(224);hist(X2,0:0.1:35);title(‘4自由度非中心X^2分布概率密度’);

%此模块用于产生四种分布的直方图以及均值和方差的检验
clc;clear;
subplot(221);x=random(‘unif’,2,5,1,1024);hist(x,2:0.1:5);title(‘2到5上均匀分布概率密度直方图’);
Mean1=3.5;
Variance1=2/3;
s1=0;
for n1=1:1024
s1=x(n1)+s1;
end
realMean1=s1/1024;
t1=0;
for n1=1:1024
t1=(x(n1)-realMean1)^2+t1;
end
realVariance1=t1/1024;

subplot(222);G1=random(‘Normal’,0,1,1,20000);hist(G1,-4:0.01:4);title(‘高斯分布概率密度直方图’);
Mean2=0;
Variance2=1;
s1=0;
for n2=1:20000
s1=G1(n2)+s1;
end
realMean2=s1/20000;
t1=0;
for n2=1:20000
t1=(G1(n2)-realMean2)^2+t1;
end
realVariance2=t1/20000;

subplot(223);G2=random(‘Normal’,0,1,1,20000);R=sqrt(G1.*G1+G2.G2);hist(R,0:0.1:5);title(‘瑞利分布概率密度直方图’);
Mean3=power(pi0.5,0.5)1;
Variance3=(2-pi0.5)*1;
s1=0;
for n1=1:20000
s1=R(n1)+s1;
end
realMean3=s1/20000;
t1=0;
for n1=1:20000
t1=(R(n1)-realMean3)^2+t1;
end
realVariance3=t1/20000;

subplot(224);G3=random(‘Normal’,0,1,1,20000);G4=random(‘Normal’,0,1,1,20000);
X=G1.*G1+G2.*G2+G3.*G3+G4.*G4;hist(X,0:0.1:30);title(‘X^2分布概率密度直方图’);
Mean4=4;
Variance4=8;
s1=0;
for n1=1:20000
s1=X(n1)+s1;
end
realMean4=s1/20000;
t1=0;
for n1=1:20000
t1=(X(n1)-realMean4)^2+t1;
end

%此模块用于产生四种分布的随机数
subplot(221);x=random(‘unif’,2,5,1,1024);plot(x);title(‘2到5上均匀分布随机数’);
subplot(222);G1=random(‘Normal’,0,1,1,20000);plot(G1);title(‘高斯分布随机数’);
subplot(223);G2=random(‘Normal’,0,1,1,20000);R=sqrt(G1.*G1+G2.*G2);plot®;title(‘瑞利分布随机数’);
subplot(224);G3=random(‘Normal’,0,1,1,20000);G4=random(‘Normal’,0,1,1,20000);
X=G1.*G1+G2.*G2+G3.*G3+G4.*G4;plot(X);title(‘X^2分布随机数’);
%不同自由度下的卡方分布概率密度
N=20000;
G1=random(‘Normal’,0,1,1,N);
G2=random(‘Normal’,0,1,1,N);
G3=random(‘Normal’,0,1,1,N);
G4=random(‘Normal’,0,1,1,N);
G5=random(‘Normal’,0,1,1,N);
G6=random(‘Normal’,0,1,1,N);
G7=random(‘Normal’,0,1,1,N);
G8=random(‘Normal’,0,1,1,N);
R1=G1.*G1+G2.*G2;%二自由度卡方分布
R2=G1.*G1+G2.*G2+G3.*G3;%三自由度卡方分布
R3=G1.*G1+G2.*G2+G3.*G3+G4.*G4;%四自由度卡方分布
R4=G1.*G1+G2.*G2+G3.*G3+G4.*G4+G5.*G5;%五自由度卡方分布
R5=G1.*G1+G2.*G2+G3.*G3+G4.*G4+G5.*G5+G6.*G6;%六自由度卡方分布
subplot(321);hist(R1,0:0.1:20);%二自由度卡方=指数分布
R8=G1.*G1+G2.*G2+G3.*G3+G4.*G4+G5.*G5+G6.*G6+G7.*G7+G8.*G8;
subplot(322);hist(R2,0:0.1:20);
subplot(323);hist(R3,0:0.2:24);
subplot(324);hist(R4,0:0.25:25);
subplot(325);hist(R5,0:0.1:30);

%本脚本用于产生不同自由度下的瑞利分布概率密度
N=20000;
g=-5:0.1:5;
G1=random(‘Normal’,0,1,1,N);
G2=random(‘Normal’,0,1,1,N);
G3=random(‘Normal’,0,1,1,N);
G4=random(‘Normal’,0,1,1,N);
G5=random(‘Normal’,0,1,1,N);
G6=random(‘Normal’,0,1,1,N);
R1=sqrt(G1.*G1+G2.*G2);%瑞利分布
R2=sqrt(G1.*G1+G2.*G2+G3.*G3);%三自由度广义瑞利分布
R3=sqrt(G1.*G1+G2.*G2+G3.*G3+G4.*G4);%四自由度广义瑞利分布
R4=sqrt(G1.*G1+G2.*G2+G3.*G3+G4.*G4+G5.*G5);%五自由度广义瑞利分布
R5=sqrt(G1.*G1+G2.*G2+G3.*G3+G4.*G4+G5.*G5+G6.*G6);%六自由度广义瑞利分布
subplot(321);hist(G1,g);%画出高斯分布
subplot(322);hist(R1,0:0.05:5);
subplot(323);hist(R2,0:0.05:10);
subplot(324);hist(R3,0:0.01:15);
subplot(325);hist(R4,0:0.15:20);
subplot(326);hist(R5,0:0.01:25);

%本模块用于产生均匀分布随机序列求和的图形
X0=random(‘unif’,0,1,1,1024);
X1=random(‘unif’,0,1,1,1024);
X2=random(‘unif’,0,1,1,1024);
X3=random(‘unif’,0,1,1,1024);
X4=random(‘unif’,0,1,1,1024);
X5=random(‘unif’,0,1,1,1024);
X6=random(‘unif’,0,1,1,1024);
X7=random(‘unif’,0,1,1,1024);
X8=random(‘unif’,0,1,1,1024);
X9=random(‘unif’,0,1,1,1024);
G=random(‘normal’,0,1,1,1024);
Y0=X0+X1;
Y1=X0+X1+X2+X3+X4+X5;
Y2=X0+X1+X2+X3+X4+X5+X6+X7+X8+X9;
subplot(221);hist(Y0,0:0.2:2);title(‘2组均匀分布随机数之和的概率密度’);
subplot(222);hist(Y1,0:0.2:6);title(‘5组均匀分布随机数之和的概率密度’);
subplot(223);hist(Y2,0:0.2:8);title(‘9组均匀分布随机数之和的概率密度’);
subplot(224);hist(G,-4:0.2:4);title(‘高斯分布随机数直方图’)

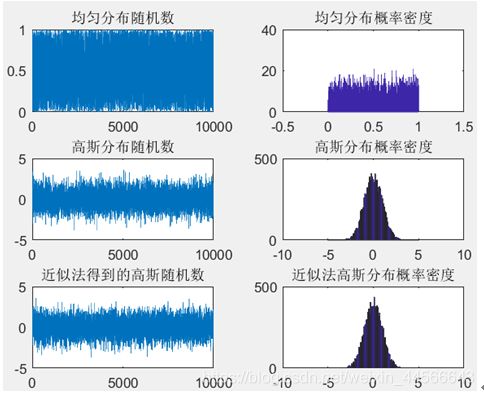
%均匀分布，高斯分布随机数的产生与仿真，概率密度观察
x=random(‘unif’,0,1,1,10000);
y=random(‘normal’,0,1,1,10000);
z=GaussRandomnumber_2(10000,0,1);
subplot(321),plot(x);title(‘均匀分布随机数’);
subplot(322);hist(x,0:0.001:1);title(‘均匀分布概率密度’);
subplot(323);plot(y);title(‘高斯分布随机数’);
subplot(324);hist(y,-5:0.1:5);title(‘高斯分布概率密度’);
subplot(325);plot(z);title(‘近似法得到的高斯随机数’);
subplot(326);hist(z,-5:0.1:5);title(‘近似法高斯分布概率密度’);

%用于自相关函数估计
N=256;
xn=random(‘normal’,0,1,1,N);
Rx=xcorr(xn,‘biased’);
m=-N+1:N-1;
subplot(211);plot(m,Rx);title(‘均值为0，方差为1的高斯分布的自相关函数’);
axis([-N N-1 -0.5 1.5]);

N=256;
xn=random(‘normal’,1,1,1,N);
Xk=fft(xn,2*N);
Rx=ifft((abs(Xk).^2)/N);
m=-N:N-1;
subplot(212);plot(m,fftshift(Rx));
title(‘均值为1，方差为1的高斯分布的自相关函数’);
axis([-N N-1 -0.5 1.5]);

%用于功率谱密度估计
N=256;
x1=random(‘normal’,0,1,1,N);
Rx1=xcorr(x1,‘biased’);
subplot(221);
m=-N+1:N-1;
subplot(221);plot(m,Rx1);title(‘均值为0，方差为1的高斯分布的自相关函数’);
axis([-N N-1 -0.5 1.5]);

subplot(222)
Sx1=abs(fft(Rx1));
plot(10*log10(Sx1));
title(‘均值为0，方差为1的高斯分布的功率谱密度’);
xlabel(‘f/Hz’);
ylabel(‘Sx1/dB’);

N=256;
xn=random(‘normal’,1,1,1,N);
Xk=fft(xn,2*N);
Rx2=ifft((abs(Xk).^2)/N);
m=-N:N-1;
subplot(223);plot(m,fftshift(Rx2));
title(‘均值为1，方差为1的高斯分布的自相关函数’);
axis([-N N-1 -0.5 1.5]);

subplot(224)
Sx2=abs(fft(Rx2));
plot(10*log10(Sx2));
title(‘均值为1，方差为1的高斯分布的功率谱密度’);

%随机信号加白噪声通过高通滤波器
clear;
N=2000;fs=400;
Nn=random(‘normal’,0,1,1,N);
t=(0:N-1)/fs;
fi=random(‘unif’,0,1,1,2)2pi;
x1=sin(2pi50t+fi(1))+sin(2pi70t+fi(2))+Nn;
Rx1=xcorr(x1,‘biased’);
subplot(231);
plot(Rx1);
title(‘通过系统前的自相关函数’);
subplot(232);
Sx1=abs(fft(Rx1,2N));
plot(10log10(Sx1));
title(‘通过系统前的功率谱密度’);
xlabel(‘f/Hz’);
ylabel(‘Sx1/dB’);

%设计一个高通滤波器
h=fir1(100,0.6,‘high’);%阶数为100，截止频率为0.6
H=fft(h,2N);
HW=abs(H).^2;
Sx=abs(fftshift(fft(x1,2N)).^2)/(2N);
Sy=Sx.HW;
Ry=fftshift(ifft(Sy));
f=(-N:N-1)fs/(2N);
m=(-N:N-1);
subplot(233);plot((-N:N-1)/N,fftshift(abs(HW(1:2N))));
title(‘高通滤波器’);
subplot(234);plot(m,Ry);
xlabel(‘f/Hz’);
ylabel(‘Ry(m)’);
subplot(235);plot(f,fftshift(10log10(Sy(1:2*N))));
title(‘x1经高通滤波器之后的自相关函数’);
axis([-200 200 -20 20]);
xlabel(‘f/Hz’);
ylabel(‘Sy/dB’);