自动驾驶控制算法(一) - 三个坐标系和车辆运动学模型

• 个人主页: 同学来啦
• 版权: 本文由【同学来啦】原创、在CSDN首发、需要转载请联系博主
• 如果文章对你有帮助，欢迎关注、点赞、收藏和订阅专栏哦

题外话

对于自动驾驶领域而言，博主顶多算是一枚非专业爱好者，对该领域有一定的兴趣，后续会重点分系列讲讲控制和决策规划算法（按照先控制后决策规划的次序），持续更新，有不对之处，欢迎大家指正，共同进步！

• ☕ 自动驾驶关键技术：
  自动驾驶关键技术可分为环境感知、行为决策、路径规划和运动控制等四个部分，其中，1）环境感知和行为决策部分技术路线不确定，每个路线方向都有各自的优缺点，学起来相对较难；2）路径规划部分相对容易；3）运动控制部分：控制技术路线（PID、LQR、MPR等算法）相对较成熟，但难点在于实车调试，往往出现理论与实车不一致的情形。

• 自动驾驶技术学习参考书籍：
  1️⃣《Vehicle Dynamics and Control》Rajesh Rajamani (中译版：《车辆动力学及控制》王国业，江发潮 等译)
  2️⃣《无人驾驶车辆模型预测控制》(第二版) 龚建伟
  以上两本书籍可作为较好的参考资料，1）1️⃣有中英两个版本，如果觉得英文版看起来比较吃力，可以看中译版，百度Apollo中控制模块就是基于该书来设计实现；2）2️⃣相比于第一版已有较大改进，但仍存在不少错误，在阅读的时候建议带着辩证的眼光去看。

一、坐标系

1、坐标系定义

坐标系基本定义：过空间定点O作三条互相垂直的数轴，它们都以O为原点，具有相同的单位长度。这三条数轴分别称为X轴（横轴）、Y轴（纵轴）、Z轴（竖轴），统称为坐标轴，这样构成一个三维笛卡尔坐标系。

那么有个问题，我们该如何确定不同坐标轴之间的顺序呢，比如，在确定了X轴之后，Y轴究竟应该在X轴的左边还是右边？Z轴应该指向天花板还是指向地板呢？那么就有必要引入右手坐标系和左手坐标系的概念。

1.1 左/右手坐标系定义

在左手坐标系中，使用左手大拇指指向X轴，食指指向Y轴，中指指向Z轴，如下图所示

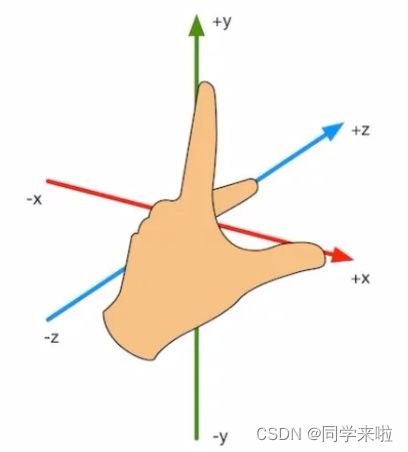
在右手坐标系中，我们使用右手的大拇指指向X轴，食指指向Y轴，中指指向Z轴，如下图所示：

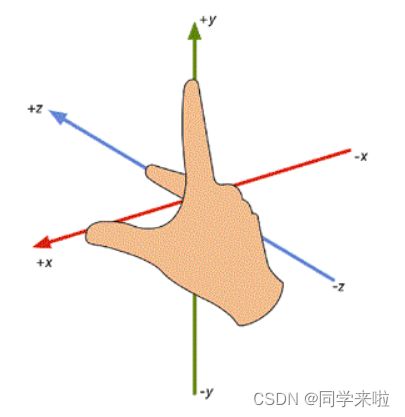
在确定不同坐标轴顺序之后，需要确定旋转角正负问题，遵循以下原则：从轴的正方向看向原点，左手坐标系下顺时针方向为旋转正向，右手坐标系下逆时针方向为旋转正向，左右手坐标系的区别，就是某一坐标轴的方向相反。

1.2 左/右手坐标系适用

针对不同的应用场景，左手坐标系和右手坐标系的适用条件也是有所不同。一般在计算机图形或视觉中通常使用的是左手坐标系，而在数学、物理中使用的则是右手坐标系，由于自动驾驶作为一门交叉学科，往往存在计算机专业和传统工科等不同专业的人们涉猎自动驾驶控制岗位，所以采用不同的坐标系，可能会导致统一物理量的正负不同，将会在初期给不少人带来很大的困扰，这点需要特别注意。

需要说明的是，为了保持统一，后续的推导过程一律采用右手坐标系 。

2、常用坐标系

下面我们介绍自动驾驶中常见的三个坐标系，包括大地坐标系（即绝对坐标系）、车辆坐标系（又称车身坐标系）、自然坐标系（即Frenet坐标系）等。

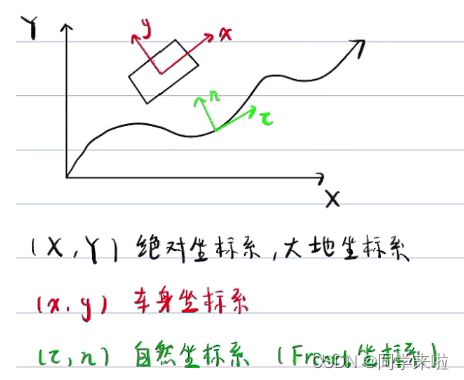
2.1 大地坐标系

大地坐标系是大地测量中以参考椭球面为基准面建立起来的坐标系。地面点的位置用大地经度、大地纬度和大地高度表示。大地坐标系的确立包括选择一个椭球、对椭球进行定位和确定大地起算数据。

2.2 车辆坐标系

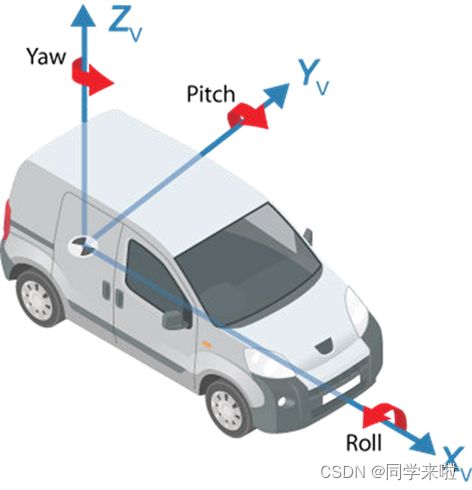
车辆坐标系是用来描述汽车运动的特殊动坐标系，其原点与质心重合，当车辆在水平路面上处于静止状态，X轴平行于地面指向车辆前方，Z轴通过汽车质心指向上方，Y轴指向驾驶员的左侧。

2.3 自然坐标系

自然坐标系（即Frenet坐标系）是沿质点的运动轨道建立的坐标系，在质点运动轨道上任取一点作为坐标原点O，质点在任意时刻的位置，都可用它到坐标原点O的轨迹的长度来表示。

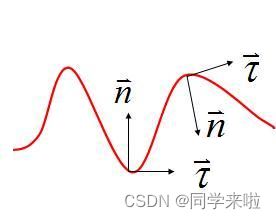
在自然坐标系中，两个单位矢量是这样定义的：
切向单位矢量：沿质点所在点的轨道切线方向
法向单位矢量：垂直于在同一点的切向单位矢量而指向曲线的凹侧

可见这两个单位矢量的方向，也是随质点位置的不同而不同的。质点运动时，根据切向和法向加速度情况，有如下特点：
1）变速直线运动：若有切向加速度且无法向加速度，则速度不改变方向而只改变大小。
2）匀速曲线运动：若有法向加速度且无切向加速度，则速度只改变方向而不改变大小。

那么为什么需要使用自然坐标系（Frenet坐标系），其主要有以下特点：
1️⃣ Frenet坐标系可以将横向控制和纵向控制解耦，有效减少计算量；
2️⃣ 可以与轨迹规划的坐标系相对应。

二、车辆运动学模型

在自动驾驶系统中，有车辆运动学模型和车辆动力学模型，其中运动学模型研究几何关系（即物体的位置和姿态），而动力学模型研究牛顿力学（即物体的线速度和角速度）。

1、运动学模型介绍

本文先介绍下车辆运动学模型，采用单车模型来模拟四轮车辆的运动模型，即单车模型把车辆的两个前轮用一个车轮代替，两个后轮也用一个车轮代替，由于车辆常常是后轮驱动，前轮转向，故在推导模型可假设后轮转向角=0。

• 运动学模型的限定条件：
  1️⃣ 车辆低速行驶，忽略轮胎的侧偏特性，点A和点B的速度方向就是前轮和后轮的方向；
  2️⃣ 仅考虑车辆在XOY平面上的运动，即前后，左右，以及绕Z轴的旋转；
  3️⃣ 假设两个前轮转向角一样，可合并为一个轮胎，应用单车模型；
  4️⃣ 车身及悬架系统是刚架结构。

车辆侧向运动学模型示意图给出如下：

图1 车辆运动学模型示意图

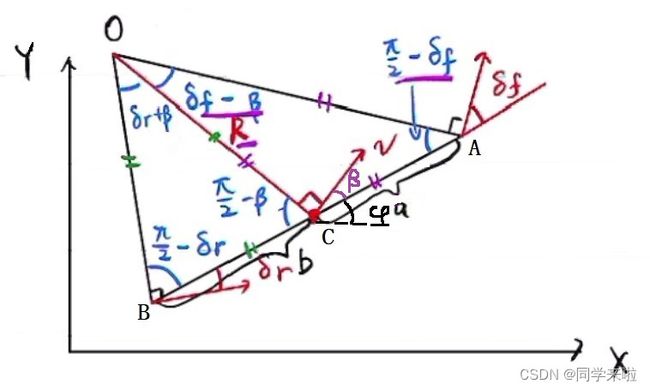
图中各个物理量含义如下表1：

物理量	含义	物理量	含义
$A$	前轮中心	$a$	前悬长度
$B$	后轮中心	$b$	后悬长度
$C$	车辆质心	$\beta$	质心侧偏角
$O$	转向圆心	$\phi$	横摆角
$v$	质心车速	$\delta f$	前轮偏角
$R$	转向半径	$\delta r$	后轮偏角

对于表中的有些物理量，是利用不同的坐标系进行定义，说明如下：
①质心侧偏角$\beta$、前轮转角$\delta f$、后轮转角$\delta r$，均定义在车身坐标系下；
②车辆横摆角$\phi$，是定义在大地坐标系下。
则车辆的航向角为：$\theta =\beta +\phi$

2、运动学方程推导

对图1，进行矢量分解可以得到
$\dot{X}=vcos(\beta +\phi )$

$\dot{Y}=vsin(\beta +\phi )$

$\dot{\phi }=\frac{v}{R}$

根据正弦定理，则有：
$\frac{a}{sin({\delta }_f-\beta )}=\frac{R}{sin(\pi /2-{\delta }_f)}$ （1）

$\frac{b}{sin({\delta }_r+\beta )}=\frac{R}{sin(\pi /2-{\delta }_r)}$ （2）

由公式（1）得到：$\frac{a}{R}=\frac{sin({\delta }_f-\beta )}{sin(\pi /2-{\delta }_f)}=\frac{sin({\delta }_f)cos\beta -sin\beta cos({\delta }_f))}{cos({\delta }_f)}=tan{\delta }_{f}cos\beta -sin\beta$ （3）

由公式（2）得到：$\frac{b}{R}=\frac{sin({\delta }_r+\beta )}{sin(\pi /2-{\delta }_r)}=\frac{sin({\delta }_r)cos\beta +sin\beta cos({\delta }_r))}{cos({\delta }_r)}=tan{\delta }_{r}cos\beta +sin\beta$ （4）

结合公式（3）和（4）则有：

$\frac{a+b}{R}=(tan({\delta }_f)+tan({\delta }_r))cos\beta$

令L = a+b 为车的轴距，得出 $\frac{1}{R}=\frac{(tan({\delta }_f)+tan({\delta }_r))cos\beta }{L}$

运动学方程变为：
$\dot{X}=vcos(\beta +\phi )$

$\dot{Y}=vsin(\beta +\phi )$

$\dot{\phi }=\frac{v(tan({\delta }_f)+tan({\delta }_r))cos\beta }{L}$

条件假设：

• 1️⃣ 低速条件下认为车不会发生侧向滑动，即$v_y\approx 0$，所以有$\beta \approx 0，cos\beta \approx 1$
• 2️⃣ 低速条件下认为车辆的后轮不转向，即${\delta }_r=0$

则车辆运动学方程最终可表示为：

X轴方向速度分量：$\dot{X}=vcos(\beta +\phi )$

Y轴方向速度分量：$\dot{Y}=vsin(\beta +\phi )$

角速度矢量： $\dot{\phi }=\frac{v(tan{\delta }_f)}{L}$

其中$v$为质心车速，$\beta$为质加粗样式心侧偏角、$\phi$为车辆横摆角，${\delta }_f$为前轮转角、$L$为车的轴距。