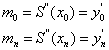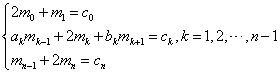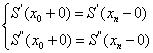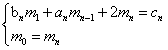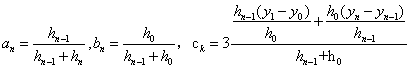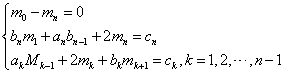三次样条插值 C#代码实现
一、样条函数的定义
样条函数属于分段光滑插值,他的基本思想是,在由两相邻节点所构成的每一个小区间内用低次多项式来逼近,并且在各结点的连接处又保证是光滑的(即导数连续)。
设在区间[a,b]上给定一组结点X:
![]() ,和一组对应的函数值
,和一组对应的函数值![]() 。若函数S(x)满足下列条件:
。若函数S(x)满足下列条件:
(1)在每一个子区间![]() (k=1,2,...n)上,S(x)是一个不超过三次的多项式。
(k=1,2,...n)上,S(x)是一个不超过三次的多项式。
(2)在每一个结点上满足S(xi)=yi,i=0,1,...,n。
(3)S(x)在区间[a,b]上为二次连续可微函数。
则称S(x)为结点X上插值与Y的三次样条插值。
二、三次样条函数的构造
在工程上,构造三次样条插值函数通常有两种方法:一是以给定插值结点处得二阶导数值作为未知数来求解,而工程上称二阶导数为弯矩,因此,这种方法成为三弯矩插值。二是以给定插值结点处得一阶导数作为未知数来求解,而一阶导数右称为斜率,因此,这种方法称为三斜率插值。
三斜率插值法
根据定义,三次样条函数在插值结点处一阶导数应存在。因此设各结点处的一阶导数为:
![]() 。利用两点埃尔米特插值公式,就可以得到样条插值函数S(x)在子区间
。利用两点埃尔米特插值公式,就可以得到样条插值函数S(x)在子区间![]() 上的表达式为:
上的表达式为:
其中:![]() 。由此可知只要确定各结点的一阶导数值mk(k=0,1,2....n),则各子区间上的三次样条插值函数S(x)也就确定了。
。由此可知只要确定各结点的一阶导数值mk(k=0,1,2....n),则各子区间上的三次样条插值函数S(x)也就确定了。
由于S(x)在区间[a,b]上的二阶导数是连续的,即在各结点的左右两子区间上的S(x)虽然不同,但在连接点的二阶导数存在,即在连接点处的二阶左导数与二阶右导数相等:![]() 。分别求子区间[xk-1,xk]右端点xk上的二阶左导数
。分别求子区间[xk-1,xk]右端点xk上的二阶左导数![]() ,以及子区间[xk,xk+1]左端点xk上的右导数
,以及子区间[xk,xk+1]左端点xk上的右导数![]() ,即可得到:
,即可得到:
![]() ,(2)与
,(2)与![]() ,(3) 整理后可得:
,(3) 整理后可得:![]() ,k=1,2,...n-1,(4)。
,k=1,2,...n-1,(4)。
其中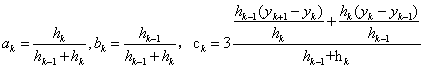 ,并且ak+bk=1。由于有n+1个插值点,因此需要确定n+1个m(m0,m1,...,mn)。而现在方程组只有n-1个方程(公式(4)),因此还需要另外补充两个条件财能唯一确定n+1个m。在实际应用中,这两个条件可以根据实际的物理意义所给出的边界条件来得到。实际问题中常用的三种边界条件如下:
,并且ak+bk=1。由于有n+1个插值点,因此需要确定n+1个m(m0,m1,...,mn)。而现在方程组只有n-1个方程(公式(4)),因此还需要另外补充两个条件财能唯一确定n+1个m。在实际应用中,这两个条件可以根据实际的物理意义所给出的边界条件来得到。实际问题中常用的三种边界条件如下:
(1)给定区间两个端点处的一阶导数值,即
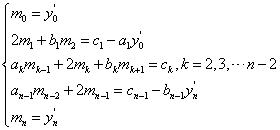 方程组的系数矩阵为
方程组的系数矩阵为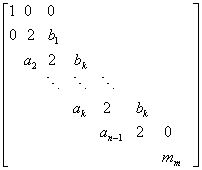 ,可知此矩阵为三对角矩阵。因此方程组可用追赶法求解。
,可知此矩阵为三对角矩阵。因此方程组可用追赶法求解。
解出mk后,即得到各结点的一阶导数值,将mk带入各结点的二阶导数值得表达式公式(2)或(3)可求得各结点的二阶导数值,将mk带入各区间上S(x)的表达式公式(1)即可得到各子区间上的三次样条插值函数S(x)。
(2)给定区间两个端点处得二阶到数值,即
![]() ,由此可得两个补充方程
,由此可得两个补充方程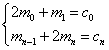 ,其中
,其中![]() 。与公式(4)联立可得如下方程组:
。与公式(4)联立可得如下方程组:
(3)插值函数为周期函数
在此给出第一种边界条件下三次样条插值的C#算法实现:
1、实现三次样条插值封装的类:
///
/// 插值
///
public static class SplineMath
{
///
/// 三次样条插值
///
/// 排序好的数
/// 需要计算的插值点
/// 写1
/// 返回计算好的数值
public static double[] SplineInsertPoint(PointClass[] points, double[] xs, int chf)
{
int plength = points.Length;
double[] h = new double[plength];
double[] f = new double[plength];
double[] l = new double[plength];
double[] v = new double[plength];
double[] g = new double[plength];
for (int i = 0; i < plength - 1; i++)
{
h[i] = points[i + 1].x - points[i].x;
f[i] = (points[i + 1].y - points[i].y) / h[i];
}
for (int i = 1; i < plength - 1; i++)
{
l[i] = h[i] / (h[i - 1] + h[i]);
v[i] = h[i - 1] / (h[i - 1] + h[i]);
g[i] = 3 * (l[i] * f[i - 1] + v[i] * f[i]);
}
double[] b = new double[plength];
double[] tem = new double[plength];
double[] m = new double[plength];
double f0 = (points[0].y - points[1].y) / (points[0].x - points[1].x);
double fn = (points[plength - 1].y - points[plength - 2].y) / (points[plength - 1].x - points[plength - 2].x);
b[1] = v[1] / 2;
for (int i = 2; i < plength - 2; i++)
{
// Console.Write(" " + i);
b[i] = v[i] / (2 - b[i - 1] * l[i]);
}
tem[1] = g[1] / 2;
for (int i = 2; i < plength - 1; i++)
{
//Console.Write(" " + i);
tem[i] = (g[i] - l[i] * tem[i - 1]) / (2 - l[i] * b[i - 1]);
}
m[plength - 2] = tem[plength - 2];
for (int i = plength - 3; i > 0; i--)
{
//Console.Write(" " + i);
m[i] = tem[i] - b[i] * m[i + 1];
}
m[0] = 3 * f[0] / 2.0;
m[plength - 1] = fn;
int xlength = xs.Length;
double[] insertRes = new double[xlength];
for (int i = 0; i < xlength; i++)
{
int j = 0;
for (j = 0; j < plength; j++)
{
if (xs[i] < points[j].x)
break;
}
j = j - 1;
Console.WriteLine(j);
if (j == -1 || j == points.Length - 1)
{
if (j == -1)
throw new Exception("插值下边界超出");
if (j == points.Length - 1 && xs[i] == points[j].x)
insertRes[i] = points[j].y;
else
throw new Exception("插值下边界超出");
}
else
{
double p1;
p1 = (xs[i] - points[j + 1].x) / (points[j].x - points[j + 1].x);
p1 = p1 * p1;
double p2; p2 = (xs[i] - points[j].x) / (points[j + 1].x - points[j].x);
p2 = p2 * p2;
double p3; p3 = p1 * (1 + 2 * (xs[i] - points[j].x) / (points[j + 1].x - points[j].x)) * points[j].y + p2 * (1 + 2 * (xs[i] - points[j + 1].x) / (points[j].x - points[j + 1].x)) * points[j + 1].y;
double p4; p4 = p1 * (xs[i] - points[j].x) * m[j] + p2 * (xs[i] - points[j + 1].x) * m[j + 1];
// Console.WriteLine(m[j] + " " + m[j + 1] + " " + j);
p4 = p4 + p3;
insertRes[i] = p4;
//Console.WriteLine("f(" + xs[i] + ")= " + p4);
}
}
//Console.ReadLine();
return insertRes;
}
}
2、插值前需要对数据进行排序,需要使用PointClass类:
public class PointClass
{
public double x = 0;
public double y = 0;
public PointClass()
{
x = 0; y = 0;
}
//-------写一个排序函数,使得输入的点按顺序排列,是因为插值算法的要求是,x轴递增有序的---------
public static PointClass[] DeSortX(PointClass[] points)
{
int length = points.Length;
double temx, temy;
for (int i = 0; i < length - 1; i++)
{
for (int j = 0; j < length - i - 1; j++)
if (points[j].x > points[j + 1].x)
{
temx = points[j + 1].x;
points[j + 1].x = points[j].x;
points[j].x = temx;
temy = points[j + 1].y;
points[j + 1].y = points[j].y;
points[j].y = temy;
}
}
return points;
}
}
3、具体实现:
private void btnCalcSpline_Click(object sender, EventArgs e)
{
double[] x = {-100,-90,-80,-70,-60,-50,-40,-30,-20,-10,0,10 ,20,30,40,50,60,70,80,90,100};
double[] y = {9802,7922,6242,4762,3482,2402,1522,842,362,82,2,122,442,962,1682,2602,3722,5142,6562,8282,10202};
PointClass[] points = new PointClass[x.Length];
for (int i=0;i