备战数学建模22-数学建模论文写作规范总结
目录
一、数模论文概述
二、论文首页规范
1-论文题目规范
2-关键词规范
3-摘要写作规范
4-问题重述写作规范
5-问题分析写作规范
6-模型假设写作规范
7-符号说明注意事项
8-模型建立与求解写作规范
9-模型检验写作规范
10-模型的优缺点评价
11-参考文献写作规范
一、数模论文概述
参赛作品包括:论文和支撑材料。
数模论文共包含如下约10部分组成,论文题目黑体三号居中,摘要标题黑体四号居中,摘要内容宋体小四,关键词黑体小四,正文一级标题黑体四号居中,正文二三级标题黑体小四号居左,正文宋体小四号,数字与字母用Time New Roman,页边距上下左右各2.5厘米,论文页数最好20页左右,行距没有特殊要求,可以根据论文页数调整。
二、论文首页规范
1-论文题目规范
论文题目一般主要是两种形式:一种是:基于XXX模型/方法/理论的XXX的问题研究
另外一种是:直接对问题简化作为题目
2-关键词规范
关键词一般3-5个,最好5个,下面5部分内容,尽量涵盖,特别是主要模型和求解算法。
3-摘要写作规范
摘要需要具有代表性和独立性,能够代表你们的工作量,而且不需要读全文,也能获得本文的主要工作信息,让审阅老师在短时间了解论文内容和方法。
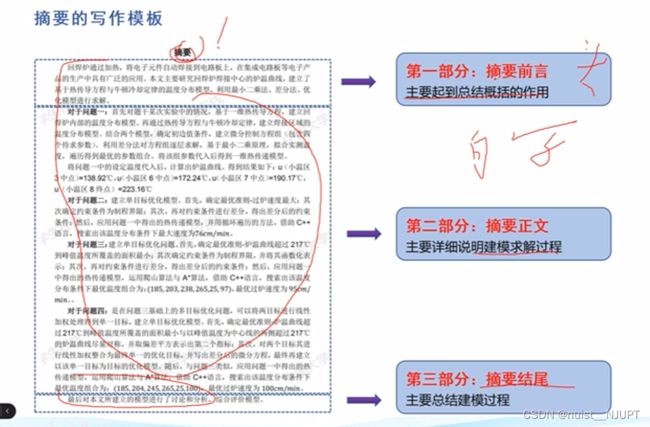
摘要应该包括三个部分:即摘要前言,摘要正文,摘要结尾;摘要前言起到总结概括的作用;摘要正文主要详细说明论文的建模和求解过程;摘要的结尾一般一句话总结建模过程。
摘要前言主要起到总结概括的作用,在撰写的时候主要包括三部分:第一,研究问题的背景和意义,第二,采用的研究思路或方法,基本上就是说模型和算法,最后是给出解决的问题,一般也就是一句话。
摘要正文部分,一般是以针对问题X开头,主要分为四部分,即简述问题,建模思路,模型求解,结果分析;
4-问题重述写作规范
问题重述的主要关键就是改写,不能抄原文,否则查重过不了,读懂题目意思,然后改写,主要包括两个部分,即背景描述和问题阐述,对于问题的阐述,可以根据实际的情况,若题目描述比较复杂,可以提炼和简化出精髓;相反,如果题目描述的过于简洁,转换为自己的语言的时候可以进行适当的扩充。
问题重述不是评审重点,但是要改写,躲过查重,还有就是问题重述不要超过一页,否则有种喧宾夺主的感觉,不好看。
我们看一下18年国一的论文,对于问题重述, 人家改写成自己的话(蓝色部分),并且根据实际情况,添加一部分内容,红色部分是添加的内容。
最后,需要说的是,第一天研究论文,并确定选题和解决方案,同时,在第一天需要把问题重述写好,不要往后拖,这个不是评分主要项,但是也要好好写。
5-问题分析写作规范
对于问题分析是我们没有建模的情况下,对问题进行解读的过程,我们需要分析已知的内容,确定要解决的问题,给出大概的求解思路,这个不要与摘要相同,分析中不要给出具体的求解结果或者具体的结论,因为还没做呢,只是分析。
我们可以看下面的原问题和问题分析,问题分析根据背景分析了问题,给出了思路和大致的结果,不是具体的结论,也不需要给出具体的模型。 问题分析是求解思路,而摘要是个求解过程。
6-模型假设写作规范
模型假设是为了简化,也就是对一些不必要的条件进行归并,也就是把一些条件排除在考虑之外,假设尽量用数学语言描述,不要描述成纯概念的问题,不能定量化的假设别乱写,
另外假设也应该合理,明显已知的没必要再写成假设,假设也应该验证合理性,一般用在灵敏度分析里。
第一种,保真性假设,就是假设题目种给出的数据都是准确无误的,统计的数据都是认真测量的。
第二种,仅考虑题目种给出的主要条件,其它非主要条件不允考虑。
第三种,对题目中的主要条件进行平稳性规定
第四种,常识性的假设,非正常的不考虑
第五种,对模型中的相关参数进行规定,防止参数对结果进行影响
7-符号说明注意事项
符号尽量用一些希腊字母,少用英字母,别用中国拼音字母;
对于全局变量,在符号说明里面给出就可以,局部变量不需要在符号说明里面给出;
特别需要注意:在符号说明中解释了的符号,在后面正文中需要再次解释。
一般符号变量10-15个左右,最好使用三线表的形式。
8-模型建立与求解写作规范
建模和求解是最重要的部分,决定最终得分的最重要的部分,模型要基本正确,不能乱用模型,也要阐明用该模型的逻辑,即为什么用这个模型,模型也不一定越复杂越好,要根据解决实际问题为原则,模型也要结合数据考虑可解性。
对于每个模型的建立,用viso绘制个流程图,有利于理解,黑框黑字,不要有背景色。
另外流程图尽量左右均衡,上下一致,不要太廋和太胖。
一般用以下几种模型建立的方式,具体如下:
对于第一种,无需建立数学模型的,以统计分析为主的,我们往往需要兼顾下面几点:
1-数据的检查和处理,异常值的检测(小波分析,微积分),空缺值得补全(插值),无量纲化处理(归一化,标准化处理),数据的降维(主成分分析之类的);
2-利用SPSS,SAS之类的统计分析软件;
3-结合精美的图标进行说明,图表的精美往往也能加分。
物理数学方面的,这种题目,没有这方面知识的不建议选择。
用的最多的就是根据已有模型建模进行求解,常见的模型可以分为几大类:评价类,预测类,优化类;
对于评价类问题,分为主观评价和客观评价
主观评价:层次分析,模糊综合评价,综合值法
客观评价:主成分分析,因子分析,Topsis,神经网络
对于预测类问题,分为短期预测(小样本)和长期预测(大样本)
中、短期预测: 灰色预测,回归分析,时间序列,微分方程;
长期预测:神经网络、logistic模型预测,微分方程预测;
优化类问题可以分为线性规划、非线性规划、二次规划
也可以分为:整数规划、0-1规划,混合整数规划
还可以分为:单目标规划,多目标规划,动态规划等
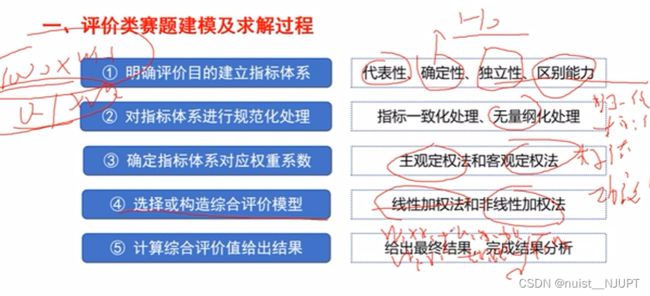
对于评价类问题,首先建立评价体系,评价的指标具有代表性,独立性,确定性和区别能力;
然后对指标进行无量纲化处理(归一化法,标准差法,极值差法,功效系数法),即数据规范化处理;
然后确定指标体系对应的权重系数,有主观定权法和客观定权法;
然后建立综合评价模型,即加权,有线性加权(指标相互独立)和非线性加权(指标不独立)两种;
最后,计算出结果,并给出结果分析;
对于预测类问题,首先需要对数据进行预处理,残缺值补全,异常值踢出;
然后根据条件,建立合适的预测模型,比如:样本大小,长期短期等;
然后对模型进行预测误差分析(绝对误差分析,相对误差分析),若误差过大,说明方法不合适,需要更换预测方法;一般用相对误差,数据比较大,误差要在0.05内,数据少,误差要在0.1内;相对误差一般不要大于0.1.
最后,给出预测结果并完成结果分析。
对于优化类问题,需要明确几个概念,即目标函数,决策变量,约束条件;需要先辨别优化模型属于哪一类,然后根据类别进行优化;
对于模型的改进的难度比较大,但是如果改进后效果比较好,可以使用;
为了使评委老师更好的理解改进后的算法,可以使用伪代码或者流程图的形式描述算法:
对于模型的改进往往很难,我们可以采用多个模型进行集成的方式,提高模型的创新型和准确度。比如对于评价类,预测类,优化类问题常常有如下的集成方式。
最后一种是设计一种全新的算法或模型,当然这个是最难的,正常不用考虑,哈哈,不过如果设计还是要注意以下几点原则:
对于模型求解部分:有结果的需要给出具体结果,注意单位,要结合题目给结果和结论,不能答非所问,对于需要解释原因和建议的,要逐列给出几条,4-5条最好。
9-模型检验写作规范
对于模型检验,我们一般在最后写,主要写的是稳定性,敏感性以及误差分析;
对于稳定性和敏感性分析:就是为了检验模型中某些参数的变化是否会引起模型的输出产生变化,我们可以根据参数的改变判断稳定性,确定适用场景,更好一些。
至于稳定性和敏感性(灵敏度)的区别:y=ax+b,稳定性就是改变b,敏感性改变a。
两种灵敏度分析情况:
一种是调整参数因子,看变化情况,如下所示:
第二种是和时间有关的,时间是横坐标,改变参数因子,画多条曲线观察,如下:
对于统计分析和误差检验,一般统计分析不会写在模型检验部分,统计及分析一般就写在模型建立部分,比如层次分析的一致性检验,相关性的假设检验,灰色模型的级比检验等;统计分析一般适用于回归分析,误差分析一般用于预测类的题目;
若改进了模型可以进行新旧模型的对比:
10-模型的优缺点评价
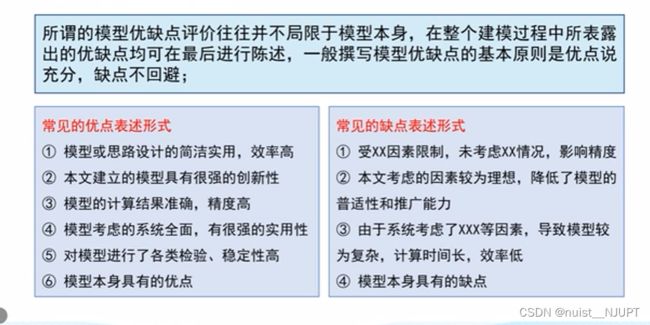
模型的优缺点表述有如下模板,对于优缺点结合实际情况,优点4-6条,缺点2-4点比较好,优点不要说的太狂,缺点也不要说的太过。优缺点合理分析最好。
11-参考文献写作规范
参考文献需要在正文中标注,上标的形式,并且参考文献要结合具体的论文,公开的资料都可以引用。
总结一下吧:所有的方法,都需要在练习中应用,否则学习的方法就没有什么意义了,加油吧,数模人,祝愿我们省国赛都取得一个好成绩!!!