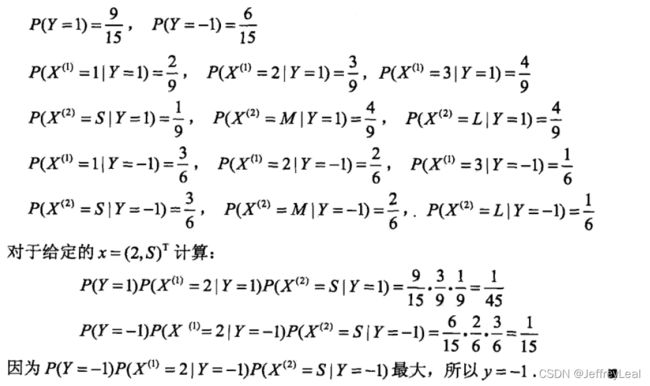电信保温杯笔记——《统计学习方法（第二版）——李航》第4章 朴素贝叶斯法

论文

电信保温杯笔记——《统计学习方法（第二版）——李航》

没有找到对应的原始论文。

介绍

本文是对原书的精读，会有大量原书的截图，同时对书上不详尽的地方进行细致解读与改写。

朴素贝叶斯法（naive Bayes）是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布，然后基于此模型，对给定的输入 $x$，利用贝叶斯定理求出后验概率最大的输出 $y$。

朴素贝叶斯法与贝叶斯估计（Bayesian estimation）是不同的概念；
特征条件独立假设的成立时，该模型称为朴素贝叶斯模型；
特征条件独立假设的不成立时，该模型称为贝叶斯网络。

特点

朴素贝叶斯法实现简单、学习与预测的效率都很高，是一种常用的方法。

数学基础

可以把事件A、B分别理解为

A	结果、证据 、（乌云、卷积云等）
B	原因、结论、（下雨、打雷等）

条件概率

$$P(B|A)=\frac{P(AB)}{P(A)}$$

全概率公式

$$P(A)=\sum _{i=1}^{n}P(A|B_i)P(B_i)$$

贝叶斯公式

又称贝叶斯定理：
$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum _{j=1}^{n}P(A|B_j)P(B_j)},i=1,2,...,n.$$
当 $i=1$时，上式退化为：
$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}.(1)$$

先验概率

此时，公式（1）中的 $P(B)$ 称为先验概率，是指根据以往经验和分析得到的概率，是在本次实验、验证之前就知道概率是固定的，不会随着观测数据或观测到的特征而改变，是频率派的主张。比如判断今日是否下雨，就以这个地区下雨的概率作为判断的依据；比如抛硬币正面的概率，则认为是1/2。

后验概率

此时，公式（1）中的 $P(B|A)$ 称为后验概率，是在给定观测值 $A$ 的条件下 $B$ 发生的概率，意味着事件 $B$ 的发生概率不能盲目的遵循以往的经验，还要基于目前观测到的特征，这是贝叶斯派的主张。比如判断今日是否下雨，在观测到事件 $A$ 乌云的条件下，下雨的概率就不能盲目地认为是这个地区下雨的概率了；再比如我们观测到一枚硬币抛1w次，正面是7k次，那么这个硬币很有可能就是做工有问题的，也不能简单地认为正面的概率就是1/2了。

似然函数

此时，公式（1）中的 $P(A|B)$ 称为似然函数，事件 $A$ 作为结果，事件 $B$ 作为原因的话，它的意义就是，基于这个原因，发生这样的结果的概率，这就是似然的意思——像这样，发生像这样的结果的概率。下面还会解释一次。

极大似然估计（MLE）

引入下面的函数
$$P(X|\theta )=\prod _{i=1}^{n}P(x_i|\theta )$$
$X$：代表观测数据，观测结果等。例如上面下雨的例子，那么这里就可以代表 $X=(x_1,x_2,...,x_n)=$（一号下雨，二号下雨，三号不下雨…），对一段时间每天下雨情况的观测；
$\theta$：代表模型的参数。在下雨的例子中，可以代表地区的经度，维度，月份，人口分布等；
$P(x|\theta )$：代表单次结果的预测模型，在下雨的例子中就是今天下雨的概率。

当模型的参数 $\theta$ 已知，此时函数 $P(X|\theta )$ 是观测数据概率分布；
当模型的参数 $\theta$ 未知，此时函数 $P(X|\theta )$ 是似然函数；
是概率分布还是似然函数，只是同一条式子的不同说法，关键不同在于模型的参数是否已知。

极大似然估计（Maximum Likelihood Estimate，MLE），就是已知观测数据 $X$ 和预测模型 $P(x|\theta )$，可得出似然函数 $P(X|\theta )$，当似然函数取得最大值时，得到参数 ${\theta }_{opt}$，即
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmax}}P(X|\theta ).(2)$$
将 ${\theta }_{opt}$ 带入预测模型得到 $P(x|{\theta }_{opt})$，就可以用于预测 $x$ 发生的概率。在下雨的例子中，就是已知过去一段时间下雨的记录，还有当天是否下雨的预测模型，得到这些天这样下雨的可能性，探究地理信息，推测 ${\theta }_{opt}=$ （这样的经度，这样的维度，这样的人口分布等），使这样下雨的可能性最大，以此地理信息用于预测当地今天是否下雨。总之，就是使结果的可能性最大，反推此时的原因。

最大后验概率估计（MAP）

最大后验概率估计（Maximum a posteriori estimation，MAP），就是已知观测数据 $X$ 、预测模型 $P(x|\theta )$、参数概率密度 $P(\theta )$，求发生这种结果，最大可能性是由于什么参数，就是求后验概率 $P(\theta |X)$ 的最大值，即
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmax}}P(\theta |X)=\underset{\theta }{\mathrm{argmax}}\frac{P(X|\theta )P(\theta )}{P(X)}$$
由于 $P(X)$ 是与参数 $\theta$ 无关的量，所以上式可以化简成
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmax}}P(\theta |X)=\underset{\theta }{\mathrm{argmax}}P(X|\theta )P(\theta ).(3)$$
将 ${\theta }_{opt}$ 带入预测模型得到 $P(x|{\theta }_{opt})$，就可以用于预测 $x$ 发生的概率。

贝叶斯估计（BE）

贝叶斯估计（Bayesian Estimation，BE）认为，实际环境中待估计量 $\theta$ 可能是一个随机变量，并且概率密度 $P(\theta )$ 已知。这时极大似然估计依然可用，但未能充分利用待估计量的信息。

代价函数

在估计某个参量 $\theta$ 时，噪声的影响会使估计产生误差，这种噪声从何而来，以下雨为例子，人口的迁移会造成人口密度的变化，工业排放也会引起空气的变化，地壳运动，板块移动，可能导致经纬度也会有稍微的变化，这个时候参数 $\theta$ 就是一个随机变量，$\theta ={\theta }_0+\sigma$，$\sigma$ 是噪声。

估计误差是要付出代价的，这种代价可以用代价函数来加以描述，记为 $c(\theta ,\hat{\theta })$，$\theta$ 是实际值，$\hat{\theta }$是估计值。代价函数有多种，这里只列举其中2种：

平方代价函数

$$c(\theta ,\hat{\theta })=(\theta ,\hat{\theta }{)}^2$$

均匀代价函数

$$c(\theta ,\hat{\theta })=\{\begin{array}{l}1|\theta -\hat{\theta }|\ge ϵ/2\\ 0|\theta -\hat{\theta }|<ϵ/2\end{array}ϵ\text{为一常数}$$
给定观测数据 $X$，估计误差的平均代价为：
$$\bar{c}(\theta |X)={\int }_{-\infty }^{\infty }c(\theta ,\hat{\theta }(X))p(\theta |X)d\theta .$$
此时贝叶斯估计的最优值为：
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmin}}\bar{c}(\theta |X)=\underset{\theta }{\mathrm{argmin}}{\int }_{-\infty }^{\infty }c(\theta ,\hat{\theta }(X))p(\theta |X)d\theta .(4)$$
将 ${\theta }_{opt}$ 带入预测模型得到 $P(x|{\theta }_{opt})$，就可以用于预测 $x$ 发生的概率。

代价函数不同时，贝叶斯估计的结果也不同。

极大似然估计、最大后验概率估计和贝叶斯估计的异同

思路

都是已知模型求参数。

极大似然估计（MLE）：使当前的结果 $P(X|\theta )$ 发生的可能性最大，再求此时的参数 $\theta$，它认为参数 $\theta$ 是一个常量；
最大后验概率估计（MAP）：直接求最可能的原因 $P(\theta |X)$，以导致这样的结果的发生；
贝叶斯估计（BE）：求猜错成本最低的原因，即使参数的估计值 $\hat{\theta }(X)$ 造成的估计误差的代价最小，求此时的 $\hat{\theta }(X)$，因为它认为参数 $\theta$ 是一个随机变量。

优化目标

极大似然估计（MLE）：
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmax}}P(X|\theta ).(2)$$
最大后验概率估计（MAP）：
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmax}}P(X|\theta )P(\theta ).(3)$$
贝叶斯估计（BE）：
$${\theta }_{opt}=\underset{\theta }{\mathrm{argmin}}{\int }_{-\infty }^{\infty }c(\theta ,\hat{\theta }(X))p(\theta |X)d\theta .(4)$$
极大似然估计与最大后验概率估计只相差了一个 $P(\theta )$，当参数 $\theta$ 的分布为均匀分布时，极大似然估计等同最大后验概率估计。最大后验概率估计实际上是在最大似然估计的基础上利用待估计参数的先验知识进行修正。

最大后验概率估计与贝叶斯估计都考虑了待估计参数 $\theta$ 的先验知识 $P(\theta )$，而最大后验概率估计是贝叶斯估计的代价函数为均匀代价的情况，且代价函数的0代价点在最大后验概率估计的估计值 ${\theta }_{map}$ ：
$$c(\theta ,\hat{\theta })=\{\begin{array}{l}1|{\theta }_{map}-\hat{\theta }|\ge ϵ/2\\ 0|{\theta }_{map}-\hat{\theta }|<ϵ/2\end{array}ϵ\text{为一常数}$$
将代价函数带入公式（4）可知，$\hat{\theta }={\theta }_{map}$ 时代价最小，此时最大后验概率估计等同贝叶斯估计。

朴素贝叶斯法原理

给定输入 $X$，最大后验概率的那个类就是预测的类别 $c_{opt}$：
$$c_{opt}=\underset{c_k}{\mathrm{argmax}}P(c_k|X).$$
要计算上式就要计算：
$$c_{opt}=\underset{c_k}{\mathrm{argmax}}P(c_k|X)=\underset{c_k}{\mathrm{argmax}}\frac{P(X|c_k)P(c_k)}{P(X)}$$
下面就是计算上式的过程：

朴素贝叶斯法的参数估计

就是估计式子（4.7）中的量。

$P(Y=c_k)$，有 $K$ 个类别，就要储存 $K$ 个参数。


$P(X^{(j)}=a_{jl}|Y=c_k)$，有 $K{\sum }_{j=1}^n{S}_j$ 种情况，就要储存 $K{\sum }_{j=1}^n{S}_j$ 个参数。

朴素贝叶斯法步骤

例子

朴素贝叶斯参数估计技巧

由于特征维度高，每个特征的取值范围也很大，分类类别也多，很容易出现样本 $X$ 没有在数据集中出现过得情况，如果直接令某个特征值的条件概率 $P(X^{(j)}=a_{jl}|Y=c_k)=0$ 的话，在累乘计算 $P(X|Y=c_k)$ 的时候就会出现等于0的情况，但概率很小和0在计算上天差地别，为解决这个问题，可以将所有不同特征取值以及类别的情况都人为添加一个样本，这样概率就不为零，总体上也没有太大的影响。

书上说这一部分为贝叶斯估计：

例子

本章概要

相关视频

相关的笔记

hktxt /Learn-Statistical-Learning-Method
详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解

相关代码

Dod-o /Statistical-Learning-Method_Code，在实际代码中，计算概率的累乘时，有可能由于接近0的累乘项 $P(X^{(j)}=a_{jl}|Y=c_k)$ 太多，而导致计算结果 ${\prod }_{j=1}^{n}P(X^{(j)}=a_{jl}|Y=c_k)$下溢，即小数实在太小了，计算机的位数也捕捉不了。使用${\sum }_{j=1}^n\log P(X^{(j)}=a_{jl}|Y=c_k)$，就能解决这个问题，保持了计算结果的单调性，又不会下溢。

pytorch

tensorflow

keras

pytorch API:

tensorflow API