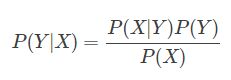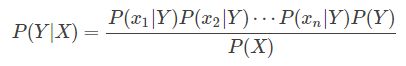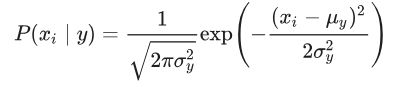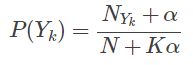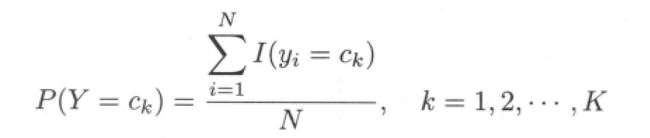机器学习——04朴素贝叶斯

机器学习的一个重要应用就是文档的自动分类。

在文档分类中，整个文档（如一封电子邮件）是实例，而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词，并把每个词作为一个特征，而每个词的出现或者不出现作为该特征的值，这样得到的特征数目就会跟词汇表中的词的数目一样多。

朴素贝叶斯是上面介绍的贝叶斯分类器的一个扩展，是用于文档分类的常用算法。下面我们会进行一些朴素贝叶斯分类的实践项目。

  

        贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类时贝叶斯分类中最简单，也是最常见的一种分类方法。

机器学习-03朴素贝叶斯

1、贝叶斯分类的基础——贝叶斯定理

        每次提到贝叶斯定理，我心中的崇敬之情都油然而生，倒不是因为这个定理多高深，而是因为它特别有用。这个定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：

      表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：。

      贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

      下面不加证明地直接给出贝叶斯定理：（证明公式可以从b站录制的视频看）

      

2、朴素贝叶斯

        朴素贝叶斯是经典的机器学习算法之一，也是为数不多的基于概率论的分类算法。对于大多数的分类算法，在所有的机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。比如决策树，KNN，逻辑回归，支持向量机等，他们都是判别方法，也就是直接学习出特征输出Y和特征X之间的关系，要么是决策函数，要么是条件分布。但是朴素贝叶斯却是生成方法，该算法原理简单，也易于实现。

    贝叶斯公式：

                                                       （X：特征向量， Y：类别）

　　先验概率P(X) 、 P(Y)：先验概率是指根据以往经验和分析得到的概率。

　　后验概率P(Y|X)：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性的大小，后验分布P(Y|X)表示事件X已经发生的前提下，事件Y发生的概率，叫做事件X发生下事件Y的条件概率。

　　后验概率P(X|Y)：通常它除以P(X)被叫做调整因子，可能性函数。在已知Y发生后X的条件概率，也由于知道Y的取值而被称为X的后验概率。

　　朴素：朴素贝叶斯算法是假设各个特征之间相互独立，然而现实生活中这样的事件不存在，也是朴素这词的意思，那么贝叶斯公式中的P(X|Y)可写成：

　　朴素贝叶斯公式：

3、朴素贝叶斯分类的原理与流程

      朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。

      朴素贝叶斯分类的正式定义如下：

      1、设为一个待分类项，而每个a为x的一个特征属性。

      2、有类别集合。

      3、计算。

      4、如果，则。

      那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

      1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

      2、统计得到在各类别下各个特征属性的条件概率估计。即。

      3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

      

      因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

      

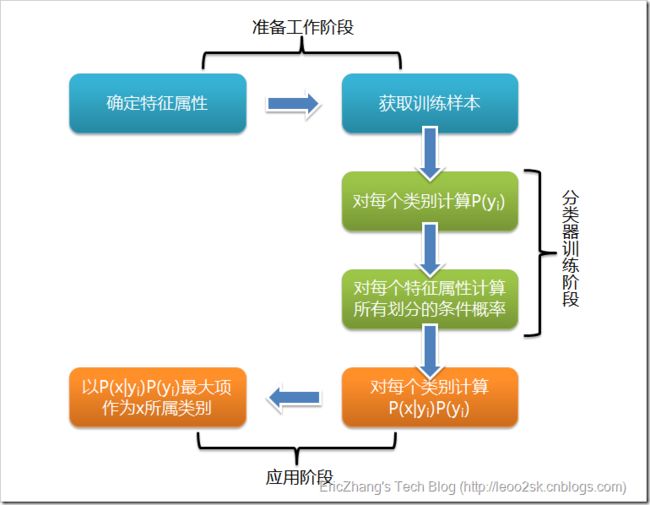
      根据上述分析，朴素贝叶斯分类的流程可以由下图表示（暂时不考虑验证）：

      可以看到，整个朴素贝叶斯分类分为三个阶段：

      第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

      第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

      第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

3.1、估计类别下特征属性划分的条件概率及Laplace校准

      这一节讨论P(a|y)的估计。

      由上文看出，计算各个划分的条件概率P(a|y)是朴素贝叶斯分类的关键性步骤，当特征属性为离散值时，只要很方便的统计训练样本中各个划分在每个类别中出现的频率即可用来估计P(a|y)，下面重点讨论特征属性是连续值的情况。

      当特征属性为连续值时，通常假定其值服从高斯分布（也称正态分布）。即：

      

      而

      因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差，代入上述公式即可得到需要的估计值。均值与标准差的计算在此不再赘述。

      另一个需要讨论的问题就是当P(a|y)=0怎么办，当某个类别下某个特征项划分没有出现时，就是产生这种现象，这会令分类器质量大大降低。为了解决这个问题，我们引入Laplace校准，它的思想非常简单，就是对没类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面。

3.2、朴素贝叶斯例子

男生、女生穿长裤还有拼写纠错

自己b站讲的视频

4、朴素贝叶斯分类实例

scikit learn（python库）将帮助在这里用Python构建Naive Bayes模型。在scikit学习库下有三种类型的朴素贝叶斯模型：

-高斯模型

          它用于分类，假设特征属于某个类别的观测值符合高斯分布。在处理连续的特征变量时，采用高斯模型。 

    当特征是连续变量的时候，假设特征分布为正态分布，根据样本算出均值和方差，再求得概率。

　　其中Ck为的第K类类别。Y的需要求出μk 和σk2 ，μk 在样本类别Ck中，所有 Xj 的平均值。σk2 为在样本类别 Ck 中，所有 Xj 的方差。

　　GaussianNB类的主要参数仅有一个，即先验概率priors，对应Y的各个类别的先验概率 P(Y=Ck)。这个值默认不给出，如果不给出此时P(Y=Ck) = mk/m。其中m为训练集样本总数量，mk为输出为第k类别的训练集样本数。如果给出的话就以priors为准。

GaussianNB(priors=None, var_smoothing=1e-09)

　　在使用GaussianNB 的 fit方法拟合数据后，我们可以进行预测。此时预测有三种方法，包括predict，predict_log_proba 和 predict_proba。

　　predict方法就是我们最常用的预测方法，直接给出测试集的预测类别输出。

　　predict_proba则不同，它会给出测试集样本在各个类别上预测的概率。容易理解，predict_proba预测出的各个类别概率里最大值对应的类别，也就是predict方法得到类别。

　　predict_log_proba 和 predict_proba类似，它会给出测试集样本在各个类别上预测的概率的一个对数转化。转化后 predict_log_proba 预测出的各个类别对数概率里的最大值对应的类别，也就是 predict 方法得到类别。

-多项式模型

           用于离散计数。例如，假设我们有文本分类问题。在这里我们可以考虑更进一步的bernoulli试验，而不是“在文档中出现的单词”，我们“计算文档中出现单词的频率”，你可以将其视为“观察到结果数x_i的次数”超过n次试验“。

多项式朴素贝叶斯常用语文本分类，特征是单词，值时单词出现的次数。

　　多项式模型在计算先验概率P(Yk)和和条件概率P(Xi|Yk)时，会做出一些平滑处理，具体公式为：

• N：样本数
• NYk：类别为Yk的样本数
• K：总的类别个数
• α：平滑值

• NYk,Xi：类别为Yk，且特征为X1的样本数
• n：特征X1可以选择的数量

-伯努利模型

        与多项式模型一样，伯努利模型适用于离散特征的情况，所不同的是，伯努利模型中每个特征的取值只能是1和0(以文本分类为例，某个单词在文档中出现过，则其特征值为1，否则为0).

 　　此时 l 只有两种取值。Xjl只能取值0或者1。

　　BernoulliNB一共有四个参数，其中三个参数的名字和意义和MultinomialNB完全相同。唯一增加的一个参数是binarize。这个参数主要是用来帮BernoulliNB处理二项分布的，可以是数值或者不输入。如果不输入，则BernoulliNB认为每个数据特征已经是二元的。否则的话，小于binarize的会归为一类，大于 binarize的会归为另外一类。

5、朴素贝叶斯的优点和缺点

优点

1）预测测试数据集很容易也很快，在多类预测中表现良好。

2）对缺失数据不太敏感，算法简单，常用于文本分类。

3）朴素贝叶斯模型有稳定的分类效率。

4）适合增量式训练，尤其是数据量超出内存时，可以一批批的去增量训练。

缺点

1）如果分类变量具有在训练数据集中未观察到的类别，则模型将指定0（零）概率并且将无法进行预测。

2）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小的时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

3）需要知道先验概率，且先验概率很多时候取决于假设。

4）通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

5）对输入数据的表达形式很敏感。

6、朴素贝叶斯算法的应用

1、实时预测

朴素贝叶斯是一个非常快速的学习分类器，因此，它可以用于实时预测。

2、多类预测

可以预测多类目标变量的概率。

3、文本分类/垃圾邮件过滤/情感分析

朴素贝叶斯分类器对于多类问题和独立性规则具有更高的成功率，因此，它被广泛用于文本分类、垃圾邮件过滤和情感分析。

4、推荐系统

 朴素贝叶斯分类器和协同过滤一起构建一个推荐系统，这有助于预测用户是否愿意提供资源。

PS:

朴素贝叶斯算法基于不同的概率估计方法具有不同的形式。概率估计方法有以下两种：

        极大似然估计
        贝叶斯估计

① 极大似然估计
可以用极大似然估计法去估计相应的概率。

先验概率 P ( Y = c k )的极大似然估计是：
 

 

 举个例子：

② 贝叶斯估计

用极大似然估计可能会出现所要估计的概率为 0 的情况，这会影响到后验概率的计算结果，使分类产生偏差。解决这一问题的方法是采用贝叶斯估计。

• 条件概率的贝叶斯估计：

  举个例子：数据同上例 4.1，按照拉普拉斯平滑估计概率：

 这里的两种估计不知道和我的视频中两种模型比较理论(最大似然和奥卡姆剃刀）有什么区别？

明天再看看