吃瓜教程——第三章

一、基本形式

给定由$d$个属性描述的示例中，$x=\left(x_1;x_2;\cdots ;x_d\right)$，其中$x_i$是$x$在第$i$个属性上的取值，线性模型表示为
$$f(x)=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$$一般情况下用向量的形式，则表示成$$f\left(x\right)=w^{T}x+b$$只要能够确定出$w$和$b$的值就可以确定这个线性模型了

二、线性回归

问：线性回归是什么？
答：线性回归是通过学习一个线性模型，来预测出其对应的连续值，通过对预测值和真实值之间，尽可能缩小其欧氏距离，即使得$f\left(x_i\right)\approx y_i$

2.1 最小二乘法

使用均方误差最小化来进行模型求解的，形如
$$\begin{gathered} E_{\left(w,b\right)}=\sum _{i=1}^m{\left(y_i-f\left(x_i\right)\right)}^2 \\ =\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2 \end{gathered}$$

2.2 极大似然估计

假设线性回归模型如下所示，
$$y=wx+b+ϵ$$
其中$ϵ$符合$$p(ϵ)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{ϵ}^2}{2{\sigma }^2}\right)$$
然后将$ϵ$用$y-(wx+b)$进行代替后，得到的式子为
$$p(y)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y-(wx+b){)}^2}{2{\sigma }^2}\right)$$
代入极大似然估计后，得到如下所示，
$$L(w,b)=\prod _{i=1}^{m}p\left(y_i\right)=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(y_i-\left(w{x}_i+b\right)\right)}^2}{2{\sigma }^2}\right)$$
由于极大似然函数不好求，因此对上述的式子进行取对数，最终得出
$$\begin{array}{rl}\ln L(w,b)& =\sum _{i=1}^m\ln \frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(y_i-w{x}_i-b\right)}^2}{2{\sigma }^2}\right)\\ & =\sum _{i=1}^m\ln \frac{1}{\sqrt{2\pi }\sigma }+\sum _{i=1}^m\ln \exp \left(-\frac{{\left(y_i-w{x}_i-b\right)}^2}{2{\sigma }^2}\right)\end{array}$$

• 其中使用了$ln(ab)=lna+lnb$的性质

2.3 求解$w$和$b$的值

加上argmin后就变成
$$\begin{gathered} \left(w^{\ast },b^{\ast }\right)=\underset{\left(w,b\right)}{\mathrm{argmin}}\sum _{i=1}^m\begin{array}{c}{\left(f\left(x_i\right)-y_i\right)}^2\end{array} \\ =\underset{\left(w,b\right)}{\mathrm{argmin}}\sum _{i=1}^m\begin{array}{c}{\left(y_i-w{x}_i-b\right)}^2\end{array} \end{gathered}$$

• 其中$argmin$表示当这个式子取最小的时候，$w$和$b$的取值是多少
  由于上述的式子中存在着两个参数一个是$w$，一个是$b$，因此对上述的式子，根据数分的知识，要求出其值，则分别对两个参数求偏导，令导数为0，即可求出连个参数的值
  最终得出$w$的求解公式为
  $$w=\frac{{\sum }_{i=1}^m{y}_i\left(x_i-\bar{x}\right)}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}{\left({\sum }_{i=1}^m{x}_i\right)}^2}$$
  $b$的求解公式是
  $$b=\frac{1}{m}\sum _{i=1}^m\left(y_i-w{x}_i\right)$$

2.4 Hessian矩阵

用于判断这个函数是否为一个凸函数的办法，Hessian矩阵形如下所示，
$${\nabla }^2{E}_{(w,b)}=\left[\begin{array}{ll}\frac{{\partial }^2{E}_{(w,b)}}{\partial w^2}& \frac{{\partial }^2{E}_{(w,b)}}{\partial w\partial b}\\ \frac{{\partial }^2{E}_{(w,b)}}{\partial b\partial w}& \frac{{\partial }^2{E}_{(w,b)}}{\partial b^2}\end{array}\right]$$
Hessian矩阵是针对于一个函数对其求二阶偏导，得出的一个矩阵，当这个矩阵为半正定的时候便可以说明这个函数为凸函数

由于在现实中不可能单单只是存在着对一维的数组进行操作，肯定会涉及到n维的欧式空间

2.5 多元线性回归

从一般的线性回归模型，到映射在n维空间上的多元线性回归，可以通过矩阵的形式表示出来，即
$$f\left({\mathbf{x}}_i\right)={\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b$$
其中$w=(w_1,w_2,...w_n)$，$x=(x_1,x_2,...x_n)$，当然从满足矩阵运算的角度来说，对哪一个进行转置都是ok的，只不过是满足一列乘以一行的规律
根据均方差误差最小化原则有
$${\mathbf{w}}^{\ast }=\arg \underset{w}{\min }(\mathbf{y}-\mathbf{X}\mathbf{w}{)}^T(\mathbf{y}-\mathbf{X}\mathbf{w})$$
对$w$进行求导
$$\frac{\partial {\mathbf{E}}_{\mathbf{w}}}{\partial \mathbf{w}}=2{\mathbf{X}}^T(\mathbf{X}\mathbf{w}-\mathbf{y})$$
令导数为0，就可以求出来$w$的解

三、对数几率回归

对数几率回归，又叫做逻辑回归，比如说将二分类的问题的结果转化为0-1上的值的输出，而最理想的单位阶跃函数是
$$y=\{\begin{array}{c}0,z<0\\ 0.5,z=0\\ 1,z>0\end{array}$$
周志华老师在书中给出这样的一幅图

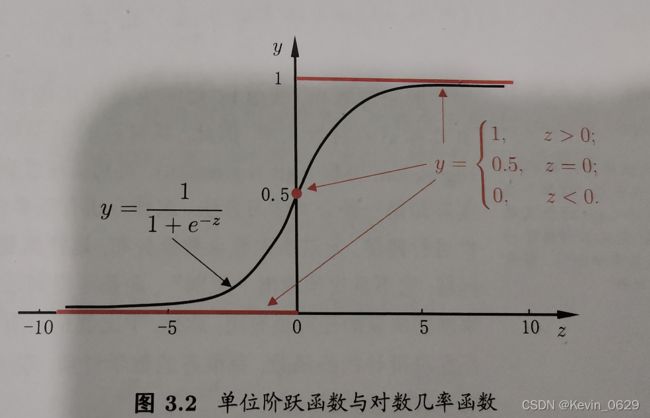
• 小心得：看到这幅图，让我想起来就在上一年的同样也是1月到2月之间，我参加了一个叫做美国大学生数学建模比赛，其中我们队对蜜蜂的那个迁移问题求解，其中就用到了这个函数的图
  针对于上述的这幅图，有一个函数可以代替图，他便是sigmoid函数
  $$y=\frac{1}{1+e^{-z}}$$
  将线性模型$y=w^{T}x+b$带入sigmoid函数中, 可以得到
  $$y=\frac{1}{1+e^{-\left({\mathbf{w}}^T\mathbf{x}+b\right)}}$$
  取对数后得到的操作如下所示
  $$\ln \frac{y}{1-y}={\mathbf{w}}^T\mathbf{x}+b$$
  采用极大似然去求解，将模型改写如下
  $$\begin{array}{rl}& p(y=1\mid \mathbf{x})=\frac{e^{{\mathbf{w}}^T\mathbf{x}+b}}{1+e^{{\mathbf{w}}^T\mathbf{x}+b}}\\ & p(y=0\mid \mathbf{x})=\frac{1}{1+e^{{\mathbf{w}}^T\mathbf{x}+b}}\end{array}$$
  得到极大似然函数，并对极大似然函数进行求对数
  $$\begin{array}{rl}L(\mathbf{w},b)& =\prod _{i=1}^{m}p\left(y_i\mid {\mathbf{x}}_i;w,b\right)\\ l(\mathbf{w},b)& =\sum _{i=1}^m\ln \left[y_i{p}_1\left({\hat{\mathbf{x}}}_i;\mathbf{w},b\right)+\left(1-y_i\right)p_0\left({\hat{\mathbf{x}}}_i;\mathbf{w},b\right)\right]\end{array}$$

四、线性判别分析(LDA)

LDA的思想很朴素，通过给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离，在书中周志华老师给出这样的一幅图，

其中正例的投影为$w^T{\mu }_0$，其协方差为$w^T{\Sigma }_{0}w$，负例的投影为$w^T{\mu }_1$，协方差为$w^T{\Sigma }_{1}w$
使得同类样例的投影点尽可能接近，则可以让下面的等式尽可能小$$w^T{\Sigma }_{0}w+w^T{\Sigma }_{1}w$$
使得异类样例的投影点尽可能远离，则可以让下面的等式尽可能大
$${\Vert w^T{\mu }_0-w^T{\mu }_1\Vert }_2^2$$
因此得到一个目标函数J
$$J_{MAX}=\frac{{\Vert w^T{\mu }_0-w^T{\mu }_1\Vert }_2^2}{w^T{\Sigma }_{0}w+w^T{\Sigma }_{1}w}$$
定义类内散度矩阵
$$\begin{gathered} S_w={\Sigma }_0+{\Sigma }_1 \\ =\sum _{x\in X_0}\left(x-{\mu }_0\right){\left(x-{\mu }_0\right)}^T+\sum _{x\in X_1}\left(x-{\mu }_1\right){\left(x-{\mu }_1\right)}^T \end{gathered}$$
以及类间散度矩阵
$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$
所以目标函数$J$可以改写成
$$J=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$$

五、多分类学习

• 一对一(OvO)
• 一对多(OvR)
• 多对多(MvM)

六、类别不平衡

情境：当数据集中，正例和负例的不多的时候，需要对其进行重新采样
再缩放思想
解决类别不平衡的三类做法

• 直接对训练集里的反类样例进行"欠采样"，即去除一些反例使得正反例数目接近
• 对训练集里的正类样例进行"过采样"，即增加一些正例使得正反例数目接近，然后再学习
• 直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，称为"阈值移动"

七、总结

首先，我觉得通过不断的写这种博客，一来能够强迫我自己每天都要去学习，对自己来说是一种监督，其次第二也让我对机器学习这本书的公式推导有一定的了解，虽然了解的还不够彻底，但是相比于之前还是有进步的，然后也学到了不少的latex的语法，说回正题，在本章学习中，由于之前期末考试月，前面存在着一些遗留的环节，因此对前面遗留的部分已经全部补回来了，所以这一章存在着一定的缺漏，但是我会在这两天全部看完再次更新我的笔记内容
针对这一章的学习，让我对线性模型有了一定的了解，有基本形式的，有高维形式的，还要对数几率线性模型就是我们口中一直提到的逻辑回归
这里附带上前两章节的连接

• 吃瓜教程第一章
• 吃瓜教程第二章