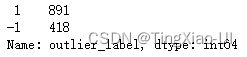TingXiao-Ul

机器学习完整项目实战附代码(一)：探索型数据分析+特征工程+建模+报告

1. 项目背景

泰坦尼克号的沉没是历史上最臭名昭著的沉船之一。1912年4月15日，在她的处女航中，被广泛认为“不沉”的“泰坦尼克号”在与冰山相撞后沉没。不幸的是，船上的每个人都没有足够的救生艇，导致2224名乘客和船员中有1502人死亡。虽然生存中有一些运气因素，但似乎有些群体比其他群体更有可能生存下来。在这里，建立一个预测模型来回答这个问题：“什么样的人更有可能生存？”使用乘客数据（即姓名，年龄，性别，社会经济阶层等）。

1.1 项目目标：

这是一个受监督的分类机器学习任务：给定一组包含目标（在本例中为幸存survived）的数据，我们希望训练一个可以学习将特征（也称为解释变量）映射到目标的模型。

监督问题：我们可以知道数据的特征和目标，我们的目标是训练可以学习两者之间映射关系的模型。
分类问题： survived是一个离散变量。

在训练中，我们希望模型能够学习特征和分数之间的关系，因此我们给出了特征和答案。然后，为了测试模型的学习效果，我们在一个从未见过答案的测试集上进行评估

使用提供的泰坦尼克号人员数据开发一个模型，该模型可以预测哪些人员生还可能性大，
然后解释结果以找到最能预测的变量。

1.2 工作流程

数据清理和格式化

探索性数据分析

特征工程：数据预处理、特征选择、[特征缩减]

基于性能指标比较几种机器学习模型

对最佳模型执行超参数调整

在测试集上评估最佳模型

解释模型结果

得出结论和报告

1.3 导入库

项目需要的工具

使用标准的数据科学和机器学习库：numpy,pandas和sckit-learn

使用matplotlib和seaborn进行可视化

输入缺失值和缩放值:sklearn.impute,sklearn.preprocessing

机器学习模型：

把数据分为训练集和测试集：from sklearn.model_selection import train_test_split

超参数调整：from sklearn.model_selection import RandomizedSearchCV, GridSearchCV

复制对象：copy

解释模型：lime

#用于数据操作的pandas和numpy
import numpy as np
import pandas as pd
#设置DataFram显示数量
pd.set_option('display.max_column',60)#最多显示60列
#可视化工具包
import matplotlib.pyplot as plt
import seaborn as sea
# 如遇中文显示问题可加入以下代码
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
# 复制对象
import copy

2. 数据清理和格式化

2.1 加载并检查数据

# 把数据读入 pandas DataFrame
data_raw=pd.read_excel(r'./Data/Titanic Dataset/titanic3.xls')
data_clean= copy.deepcopy(data_raw)
#查看数据
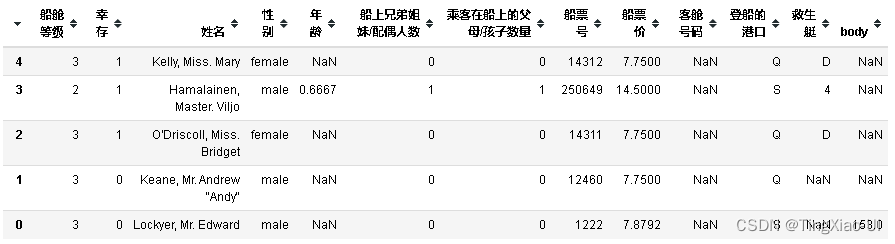
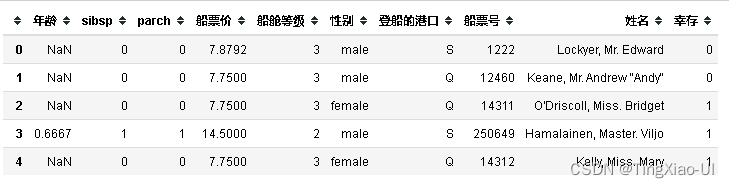
data_clean.head()

#查看数据大小
data_clean.shape

加载数据后，我们要解决的问题：
1）理解数据。
我们通常会看到每一列的第一行是各种名词，就是所谓的表头，理解这些名词的含义对于处理数据非常重要，但是我们面对的数据来自各个领域，数据科学家不是精通各个领域专业知识的杂家，这时候就需要通过各种手段去理解数据：

是否幸存：1-是，0-否，为目标列。数值型

船舱等级：1/2/3:头等舱/二等舱/三等舱，头等舱更靠近救生艇。数值型

姓名：英文全名+头衔。字符串类型

性别：male/female。字符串类型

年龄：存在小于1的数值(如0.9167)，存在缺失值，字符串类型

船上兄弟姐妹/配偶人数：数值型

乘客在船上的父母/孩子数量：数值型

船票号：字符串型

船票价：与船舱等级相关，也可能乘客年龄也可能相关

客舱号码：描述用户所住的船舱编号。由两部分组成，仓位号和房间编号。字符串类型。

登船的港口：描述乘客登船的港口。字符串类型

救生艇：数值型

body：记录遇难者编号，存在缺失值，数值型。该特征包含目标信息(幸存)，容易造成数据泄露现象，建议删除该列

舱位等级越低，所居住的位置就越靠近船舱的底部。泰坦尼克号共有10层甲板（不包含高级船员住舱的屋顶），其中8层供乘客使用。救生艇甲板：该甲板位于最顶层，因两侧安放了救生艇而得名

2）识别特征类型
特征主要类型有：时间型、数值型、类别型、文本型

类别特征：类别型特征将相似属性归为一类，但是大多数模型都不能直接处理文本型数据，必须要转换为数值型才能使用。类别型特征可以分为定类变量、定序变量。

定类变量：如性别（男、女、其他），三种取值之间是相互独立的，彼此之间完全没有关系，这种变量称之为名义变量。

定序变量：如学历（小学、初中、高中），三种取值不是完全独立的，我们可以明显看出，在性质上可以有高中>初中>小学这样的联系，学历有高低，但是学历的取值之间却不是可以计算的，我们不能说小学 + 某个取值 = 初中。这是有序变量。

数值特征：数值型随样本的不同而进行变化，一般分为连续型，离散型，经常使用归一化，离散化等方法进行处理。数值型特征可以分为定距变量、定定比变量。

定距变量：如温度（>25摄氏度、>30摄氏度、>35摄氏度），各个取值之间有联系，且是可以互相计算的，而且两者的差值有意义。比如35摄氏度 - 25摄氏度 = 10摄氏度，分类之间可以通过数学计算互相转换。这是有距变量。

定比变量：如质量（>10kg、>50kg、>100kg），各个取值之间有联系，不仅可以计算差值，还可以计算其商值。

本例中：

定类变量：性别、登船的港口、是否幸存
定序变量：船舱等级：分类变量，1、2、3
混合型：船票号、客舱号、救生艇

2.2 数据类型和缺失值

'dataframe.info’方法是一种通过显示每列的数据类型和非缺失值的数量来评估数据的快速方法。注意若某列即存在字符串又存在数字，则意味着带有数字的列将不会表示为数字，因为pandas会将具有任何字符串值的列转换为所有字符串的列。

data_clean.info()

年龄字段应为数值型，将年龄字段转换为数值型特征

性别字段为分类字段-定类，将性别字段编码为0,1,即转换为数值型特征，以观察其性质，后续要one_hot编码

2.2.1 将数据转换为正确类型

data_clean['年龄']=data_clean['年龄'].astype(float)
data_clean['性别']=data_clean['性别'].replace({'male':1,'female':0})
data_clean.info()

data_clean.describe(percentiles=None, include=None, exclude=None)作用是生成数值型数据的描述性统计数据，总结数据集分布的集中趋势，分散和形状，不包括 NaN值。参数含义：

percentiles：包括在输出中的百分位数。全部应该介于0和1之间。默认值为，返回第25，第50和第75百分位数。[.25, .5, .75]

include：默认是None 结果将包括所有数字列

exclude：默认是None,结果将不包含任何内容。

对于数值数据，则结果将包括count， mean，std，min，max以及第25，第50和第75百分位数,其中第50百分位数等价于中位数。

data_clean.describe()

2.3 处理缺失值

数据存在缺失值是不可避免的现象，* 如果列中缺失值的比例很高，那么它对我们的模型可能不会有用，可以选择删除。删除列的阈值取决于实际问题。

现在已经有了正确的列数据类型，可以通过查看每列中缺失值的百分比来进行分析

可视化缺失值

import missingno as msno
msno.matrix(data_clean)
# msno.bar(data_clean)

2.3.1 删除缺失值占比大于阈值的列

计算数据特列特征缺失值数量以及比例

def missing_values_table(df):#输入：dataframe数据，输出：缺失总量即比例，降序输出
    #计算总的缺失值数量并降序处理
    mis_val = df.isnull().sum().sort_values(ascending=False)
    mis_val = mis_val[mis_val>0]#提取有缺失值的列
    #计算缺失值比例
    percent = round(mis_val* 100 /len(df),2)
    mis_val_table_ren_columns=pd.concat([mis_val,percent], axis=1, keys=['Missing Values','Percent'])
    #打印总结信息：总的列数，有数据缺失的列数
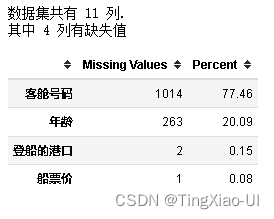
    print ("数据集共有 " + str(df.shape[1]) + " 列.\n"+"其中 " + str(mis_val_table_ren_columns.shape[0]) +
              " 列有缺失值")
    # 返回带有缺失值信息的dataframe
    return mis_val_table_ren_columns
#查看缺失值
missing_values_table(data_clean)

在处理真实世界数据时的一个常见问题是缺失值。缺失值可能是由各种原因引起的，在我们训练机器学习模型之前必须填充或删除这些缺失值。首先，让我们了解每列中有多少缺失值。如果列中缺失值的比例很高，那么它对我们的模型可能不会有用。

缺失值应该达到多少比例时才允许删除，这取决于实际问题，对于此项目：
我们将删除缺失值超过50%的列：此外，具体特征具体分析，若特征很有必要，则即使缺失值比例很高也选择保留

body特征列包含目标信息且缺失值占比达90.8%。选择直接删除处理×

救生艇对乘客能否有机会存活有很大影响，所以虽然其缺失值占比达62.87%，这里暂时先保留该列**…**

由于客舱号码可以够描述乘客居住位置，不同船舱距离甲板的距离不同，那么不同船舱的乘客能够登上甲板的顺序肯定不同，不考虑其他因素，这也会对他们能否有机会存活起到一定影响，所以虽然其缺失值占比达77.46%，这里暂时先保留该列，然后在训练模型的时候检测有无该列时对模型的影响，然后决定是否保留该各种**…**

其他字段缺失值占比低于50%，这里暂时均保留√

#删除body列
data_clean = data_clean.drop(['body','救生艇'],axis=1)

2.3.2填充缺失值

缺失项：

年龄

船票价

登船的港口

客舱号码

填充策略：

直接填充以(均值、中位数、众数)填充缺失列的值

计算相关系数，根据最相关的几个字段筛选后取值(均值、中位数、众数)来填充

计算相关系数，以最相关的几个字段为基准，选择距离最近即最相似的样本对应的值来填充(KNN)

通过模型预测填充

策略1：填充方式比较粗暴，不够合理，适用于缺失值较少

策略2：填充方式较为合理，适用于缺失值较少

策略3：KNN填充，适用于没有连片缺失的数据(比如最相似的k个样本都缺失，KNN则不在起作用)

策略4：更准确

分析年龄

由于年龄是连续字段，可以查看与其相关度最高的字段，并根据相关性最高的字段填充(均值、中位数、众数)，而不是直接粗暴的填充(均值、中位数、众数)。

计算相关系数

#计算相关系数
data_clean.corr().abs()['年龄'].sort_values(ascending=False)#ascending=False，降序，默认：True，升序

可以看到船舱等级字段和年龄字段关联度最高，其次是船上兄弟姐妹/配偶人数，那么据此将他们进行筛选，得到每个船舱等级、船上兄弟姐妹/配偶人数对应船舱等级的平均年龄，据此来填充年龄字段的缺失值。

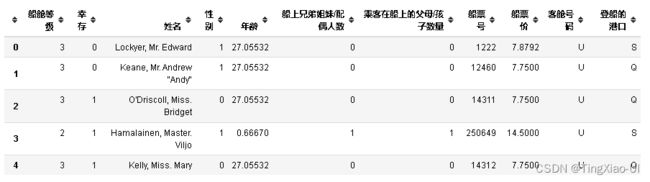
groups = data_clean[['船舱等级','船上兄弟姐妹/配偶人数','年龄']].groupby(['船舱等级','船上兄弟姐妹/配偶人数']).mean()
groups

填充年龄字段缺失值

for i in data_clean['年龄'].index:
    if pd.isnull(data_clean['年龄'][i]):
        #value_age = groups.loc['female',:].loc[1,'年龄']
        value_age = groups.loc[data_clean['船舱等级'][i],:].loc[data_clean['船上兄弟姐妹/配偶人数'][i],'年龄']
        data_clean.loc[i,'年龄']= value_age
missing_values_table(data_clean)

2. 填充登船的港口的缺失值

登船的港口字段为定类数据且缺失值较少，选择用众数进行填充

#使用港口的众数填充缺失值
value_mode = data_clean.登船的港口.dropna().mode()[0]
data_clean.登船的港口=data_clean.登船的港口.fillna(value=value_mode)
missing_values_table(data_clean)

3. 填充船票价缺失值

船票价是连续字段，可以查看与其相关度最高的字段，并根据相关性最高的字段填充(均值、中位数、众数)，而不是直接粗暴的填充(均值、中位数、众数)。

#计算相关系数
data_clean.corr().abs()['船票价'].sort_values(ascending=False)#ascending=False，降序，默认：True，升序

船票价字段与船舱等级关联度最高，其次是幸存、乘客在船上的父母/孩子数量。

由于只缺失一个数值，即没有连片缺失，所以这里采用KNN填充，根据船舱等级、幸存字段判断距离最近，寻找即最相似的的乘客对应的票价

注意关联字段不能选择幸存，因为幸存字段是目标字段，根据幸存字段来填充缺失值，会使特征空间包含目标信息，从而导致数据泄露。

def KNNImputerNum(inx,k=1):
    #inx = data_clean[['Latitude','Longitude','Borough']]
    result = copy.deepcopy(inx)
    base = copy.deepcopy(inx.iloc[:,:-1])
    col = list(result.columns)[-1]
    for row in result.index:
        if pd.isnull(result.loc[row,col]):
            #计算距离
            dis = np.linalg.norm((base-base.loc[row,:]),axis=1)
            index = dis.argsort()[k]
            while pd.isnull(inx.iloc[index,-1]) and k<dis.shape[0]:
                k+=1
                index = dis.argsort()[k]
            if k<dis.shape[0]:
                #填充缺失值
                result.loc[row,col]=inx.iloc[index,-1]
            else:
                print('无法填充，该'+col+'整列缺失！')
                return
    return result
#填充信息    
tmp =copy.deepcopy(data_clean[['船舱等级','乘客在船上的父母/孩子数量','船票价']])
data_clean[['船舱等级','乘客在船上的父母/孩子数量','船票价']]=KNNImputerNum(tmp,k=1)

missing_values_table(data_clean)

4.分析客舱号码

客舱号码缺失值比例很大，达到近78%，通常缺失项很大的特征一般会选择直接删除，但由于客舱号码特征比较重要，客舱号码特征可以反映乘客所在的位置，即可以透露出乘客距离救生艇的远近，从而影响乘客生还率这一目标，所以这里暂时先选择保留以分析其性质，并在训练模型中观察这一特征有无对模型的影响，从而决定是否保留这一特征。

客舱号码由舱位号和编号(如B5，B代表舱位，可能与船舱等级有关，5可能表示床铺号或者房间号，不同等级的船舱的床铺数也不同)

使用同一张的船票的乘客对应舱位号应相同

提取客舱号码舱位号，对客舱号统一码格式化为舱位号格式

对客舱号码字段作如下处理：

提取客舱号码字段的舱位号

根据船票号填充缺失项的舱位号

查看此时客舱号码缺失比例，若缺失比例依然很大，则缺失值替换为字母’U’（unknown）

提取客舱号码舱位号

#提取字符
import re
# grade_num = data_clean.dropna(subset=['客舱号码']).loc[:,['船舱等级','客舱号码']]
grade_num = data_clean.loc[:,['船舱等级','客舱号码']]

for i in grade_num.dropna(subset=['客舱号码']).index:
    strs = list(set(re.findall('[a-zA-Z]+',grade_num.loc[i,'客舱号码'])))
    if len(set(strs))>1:
        strs = ''.join(strs)
    else:
        strs = strs[0]
    data_clean.loc[i,'客舱号码'] = strs

#查看客舱号码字段类别
data_clean.客舱号码.unique()

根据船票号填充客舱号码缺失项

null_lists = data_clean[pd.isnull(data_clean.客舱号码)].index
# tmp = data_clean[['船票号','客舱号码']]
for i in  null_lists:
    ticket_num = data_clean.loc[i,'船票号']
    cabin_lists = set(list(data_clean[data_clean.船票号==ticket_num].客舱号码.dropna()))
    if len(cabin_lists)>0:
#         print(cabin_lists)
        data_clean.loc[i,'客舱号码']=cabin_lists

missing_values_table(data_clean)

客舱号码字段仍有大量缺失值，对缺失项统一填充为Unknown的首字母’U’。

data_clean.客舱号码=data_clean.客舱号码.fillna(value='U')
missing_values_table(data_clean)

data_clean['客舱号码'].unique()

此时可查看客舱号码与其他特征的关系图

客舱号码与船舱等级的关系

# barch(data_clean,'船舱等级','幸存')
def barch(inx,tab1,tab2):#tab1:,tab2:lenged类别
    #生成临时列
    l = len(inx[tab1].unique())
    df = pd.DataFrame(inx[tab1].unique(),columns=['tmp'])
    df.index=df['tmp'].values
    #统计每种类别(tab1)在不同类别tab2下的数量
    lists = inx[tab2].unique().tolist()
    for li in lists:
        counts = inx[tab1][inx[tab2]==li].value_counts()
        
        tmp = pd.DataFrame({str(li):counts})
        df = pd.concat([df,tmp],axis=1)
    df=df.drop(['tmp'],axis=1)#删除临时列
    
    # 添加计数列
    df_count=pd.DataFrame(df.apply(lambda x:x.sum(),axis=1),columns=['counts'])
    #生成百分比数据
    df_percentage = pd.concat([df,df_count],axis=1)
    #遍历列，计算百分比
    for col in df_percentage.columns:
        df_percentage[col]=round(df_percentage[col]/df_percentage['counts']*100,2)
    #删除原有计数列
    df_percentage = df_percentage.drop(['counts'],axis=1)
    
    #分别绘制堆积条形图和百分比堆积条形图
    fig,ax_arr = plt.subplots(1,2,figsize=(10, 5))
    
    df.plot(kind='barh', stacked=True,ax=ax_arr[0]).invert_yaxis()
    ax_arr[0].set_title(tab1+' vs '+tab2)
    ax_arr[0].set_xlabel('数量')
    ax_arr[0].set_ylabel(tab1)
    
    df_percentage.plot(kind='barh', stacked=True,ax=ax_arr[1]).invert_yaxis()
    ax_arr[1].set_title(tab1+' vs '+tab2)
    ax_arr[1].set_xlabel('百分比')
    ax_arr[1].set_ylabel(tab1)    
    
    plt.show()
    #防止文字遮挡
    plt.tight_layout()
#     return df,df_percentage

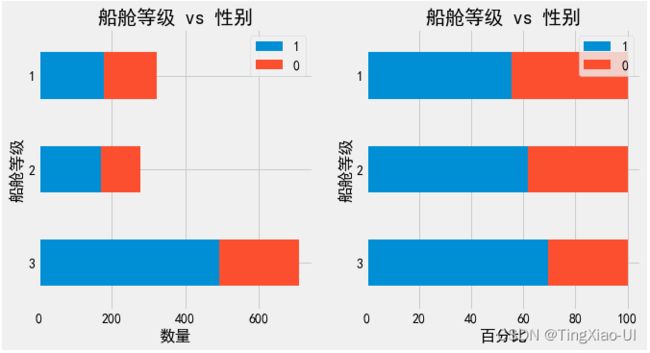
barch(data_clean,'客舱号码','船舱等级')

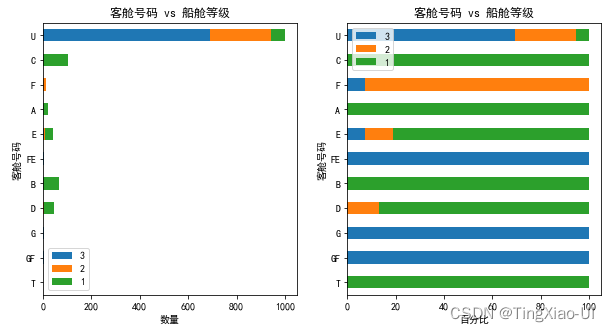
如图，可以看出客舱号码很大程度上受制于船舱等级，头等舱乘客普遍居住在ABCDET这几个舱位，二等舱乘客则分散在DEF舱位

查看各舱位等级与是否生还的关系

barch(data_clean,'客舱号码','幸存')

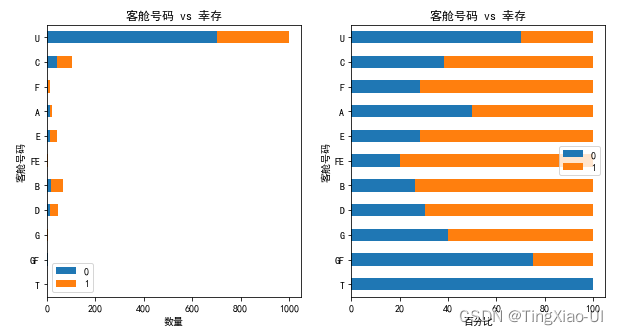
综上，虽然客舱号字段缺失值比例较大，但其与生存率有很大关联，所以暂时不做删除处理。

2.4 处理重复样本

重复样本相当于对某部分样本集合的过采集，从而很可能会提高了这部分样本在全局Loss中所占的比重，模型求解的最终结果会偏向于降低这部分样本的训练误差，而牺牲其他样本的训练误差。

如何处理重复样本？删除or保留？

假设数据采集没有问题： * 重复数据本身代表了一种真实分布，也就是你的测试集也服从这种分布，那么不该删除，因为这种重复数据表明了某种类型的数据非常重要，出现频率非常高，你的模型该以此类为优先级

由于样本各类别重复比例不一定相同，删除重复样本很可能会改变原数据集的分布的，从而影响模型。

结合实际业务分析：

结合实际业务分析，比如泰坦尼克号数据，有没有特征完全相同的样本(乘客)？姓名、年龄、性别…，本项目选择直接删除重复处理(若存在重复样本)

检查是否有重复样本

data_clean.duplicated().value_counts()

没有重复样本，不做处理。
#data_clean=data_clean.drop_duplicates()

3. 探索性数据分析

探索性数据分析(EDA)是一个开始式流程，我们制作绘图并计算统计数据，以便探索我们的数据。

目的是找到异常，模式，趋势、分布或关系。例如，找到两个变量之间的相关性、使用哪些特征可用于建模决策。

简而言之，EDA的目标是确定我们的数据可以告诉我们什么！ EDA通常以高级概述(high-level overview)开始，然后在我们找到要检查的感兴趣的区域时缩小到数据集的特定部分。

要开始EDA，我们将专注于幸存变量，它是我们的机器学习模型的目标。

通过 describe 和 matplotlib 可视化查看数据各个特征的相关统计量（柱状图）
'data.describe(percentiles=None,include=None,exclude=None)'作用是生成数值特征的描述性统计数据，总结数据集分布的集中趋势，，不包括NaN值。参数含义：

percentiles：包括在输出中的百分位数。全部应该介于0和1之间。默认值为第25，第50和第75百分位数

include:默认是None，结果将包括所有数字列

exclude:默认是None，结果将不包括任何内容。对于数字数据，则结果将包括count，mean，std，min，max以及第25，第50和第75百分位数，其中第50百分位数等价于中位数

#统计每列信息
data_clean.describe()

可视化查看数据的相关统计量（柱状图）

data_desc = data_clean.describe() # 查看数据描述
cols = data_desc.columns # 取得列缩影
index = data_desc.index[1:] # 去除count行
plt.figure(figsize=(15, 5))  # 控制画布大小
for i in range(len(cols)):
    ax = plt.subplot(2,4,i+1) # 绘制10x6的表格，当前数据特征维度为60
    ax.set_title(cols[i]) # 设置标题
    for j in range(len(index)):
        plt.bar(index[j], data_desc.loc[index[j], cols[i]]) # 对每个特征绘制describe柱状图
plt.tight_layout()#防止文字遮挡
plt.show()

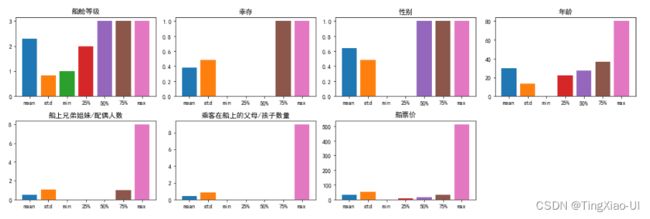
各特征数据分布较为正常，最小值，中位数，最大值是错落分布，正常分布的，且均值和标准差分布也正常。未发现方差极小(接近0)的特征。
若某个特征方差极小接近于0或者某个特征都是NaN，说明该特征对目标没有什么影响，可以选择直接删除该特征.

3.1 查看目标数据的分布情况-单变量图

目的：查看数据失衡程度、检测异常数据

目标是预测幸存，因此合理的开始是检查目标变量的分布。直方图是可视化单个变量分布的简单而有效的方法，使用matplotlib可以很容易的画出直方图。

#绘制直方图
plt.style.use('fivethirtyeight')
plt.hist(data_clean['幸存'],bins=3,edgecolor='k',density=False)
#设置坐标轴标签
plt.xlabel('是否生还')
plt.ylabel('乘客数')
#标题
plt.title('分布')

查看数据集失衡程度

class_more = data_clean['幸存'].value_counts().values[0]
class_less = data_clean['幸存'].value_counts().values[1]
print('类别比例:',data_clean['幸存'].value_counts().values/len(data_clean))
print('多数类与少数类比例：',class_more/class_less)

目标变量是分类变量，我们可以看到样本分布较倾斜，属于轻度失衡样本。一般可以把失衡分为3个程度：

轻度：20-40%

中度：1-20%

极度：<1%

3.1.1 不平衡数据集

一般来说，失衡样本在我们构建模型的时候看不出什么问题，而且往往我们还可以得到很高的accuracy，为什么呢？假设我们有一个极度失衡的样本，y=1的占比为1%，那么，我们训练的模型，会偏向于把测试集预测为0，这样子模型整体的预测准确性就会有一个很好看的数字，如果我们只是关注这个指标的话，可能就会被骗了。建立在不平衡数据集上的ML模型会难以准确预测稀有点和少数点，整体性能会受到限制。因此，识别和解决这些点的不平衡对生成模型的质量和性能是至关重要的。

对于未作平衡处理的失衡样本，需要注意保持数据类别分布不被改变：

划分数据集时要按照类别比例划分数据集为训练集和测试集

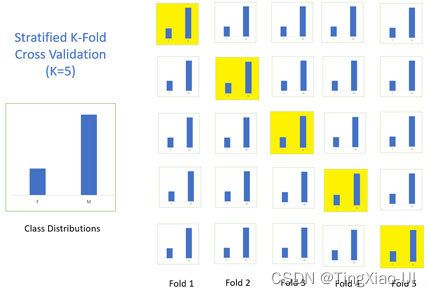
交叉验证时使用分层k折交叉验证

3.1.1.1 处理不平衡数据的理论方法

数据抽样角度：

二次采样(重采样)：欠采样、过采样。缺点：会改变数据原有分布，欠采样：具有随机性，会丢失一部分信息，欠拟合，过采样：模型容易学习到噪声导致过拟合

欠采样：是一个随机抽样一部分多数类的数据过程，这样可是时多数类数据数量可以和少数类数量相匹配

过采样：是一个生成数据的过程，即通过学习少数类样本特征随机的生成新的少数类样本数据。如SMOTE是一种过采样算法，它基于距离度量选择小类别下两个或者更多的相似样本，然后选择其中一个样本，并随机选择一定数量的邻居样本对选择的那个样本的一个属性增加噪声，每次处理一个属性。这样就构造了许多新数据

混合采样：平衡过采样和欠采样

算法模型角度：

代价敏感训练：在代价函数中赋予对少数类预测损失更大的权重。就是分类正确和分类错误的代价值是不一样的。这样就可以选择
代价最小的分类器。

在AdaBoost中，可以基于代价函数来调整错误样本权重向量D。

在朴素贝叶斯中，可以选择具有最小期望代价而不是最大概率的类别作为最后的结果。

在SVM中，可以在代价函数中对于不同的类别选择不同的惩罚因子c。 * 最佳概率截点：对于概率模型，如逻辑回归的概率截点为0.5，大于为1，小于为0。如果我们改动这个截点值，相应的预测判类也会变动。可根据多数类与少数类样本比例来调整概率截点

转换为异常点检测问题：针对极度不平衡样本，把少数类样本作为异常点，把问题转化为异常点检测问题。

工具：

随机欠采样：注意：先划分数据集后再采样，首先要明确，训练集的作用是为了学得正负样本的分割超平面，但是数据不平衡，会干扰模型的学习，因此，我们才在训练集上使用“重采样”这样的技术手段；而测试集的本质作用是利用历史样本来检验学得的模型的泛化能力，因此测试集必须要代表未来真实的样本分布，不然就丧失了测试集本身应有的作用。

# #导入库
# from imblearn.under_sampling import RandomUnderSampler
# from collections import Counter
# from sklearn.model_selection import train_test_split
# from sklearn.svm import SVC
# from sklearn.metrics import classification_report, roc_auc_score

# # 划分训练集和测试集
# X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.3)
# # 统计当前的类别占比情况
# print("Before undersampling: ", Counter(Y_train))
# # 调用方法进行欠采样
# undersample = RandomUnderSampler(sampling_strategy='majority')
# # 获得欠采样后的样本
# X_train_under, Y_train_under = undersample.fit_resample(X_train, Y_train)
# # 调用支持向量机算法 SVC
# model=SVC()
# #未欠采样
# clf = model.fit(X_train, y_train)
# pred = clf.predict(X_test)
# print("ROC AUC score for original data: ", roc_auc_score(y_test, pred))
# #欠采样
# clf_under = model.fit(X_train_under, y_train_under)
# pred_under = clf_under.predict(X_test)
# print("ROC AUC score for undersampled data: ", roc_auc_score(y_test, pred_under)

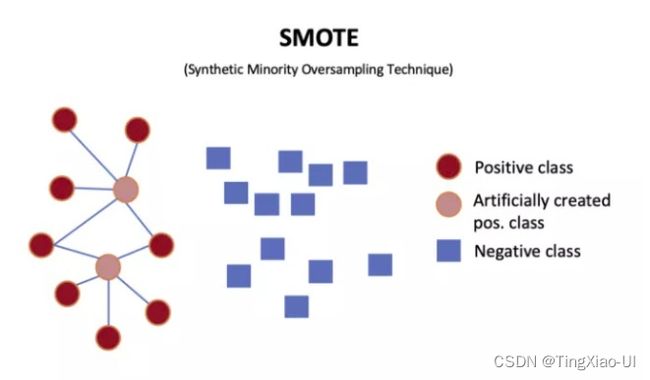
使用SMOTE进行过采样：
过采样技术中，SMOTE被认为是最为流行的数据采样算法之一，它是基于随机过采样算法的一种改良版本，由于随机过采样只是采取了简单复制样本的策略来进行样本的扩增，这样子会导致一个比较直接的问题就是过拟合。因此，SMOTE的基本思想就是对少数类样本进行分析并合成新样本添加到数据集中。
算法流程如下：(1)对于少数类中每一个样本x，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其k近邻。(2)根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数类样本x，从其k近邻中随机选择若干个样本，假设选择的近邻为xn。(3)对于每一个随机选出的近邻xn，分别与原样本按照如下的公式构建新的样本。

# # 导入相关的方法
# from imblearn.over_sampling import SMOTE
# # 划分训练集和测试集
# X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.30)
# # 统计当前的类别占比情况
# print("Before oversampling: ", Counter(y_train))
# # 调用方法进行过采样
# SMOTE = SMOTE()
# # 获得过采样后的样本
# X_train_SMOTE, y_train_SMOTE = SMOTE.fit_resample(X_train, y_train)
# # 统计过采样后的类别占比情况
# print("After oversampling: ",Counter(y_train_SMOTE))
# # 调用支持向量机算法 SVC
# model=SVC()
# #未过采样
# clf = model.fit(X_train, y_train)
# pred = clf.predict(X_test)
# print("ROC AUC score for original data: ", roc_auc_score(y_test, pred))
# #过采样
# clf_SMOTE= model.fit(X_train_SMOTE, y_train_SMOTE)
# pred_SMOTE = clf_SMOTE.predict(X_test)
# print("ROC AUC score for oversampling data: ", roc_auc_score(y_test, pred_SMOTE))

混合采样（使用pipeline）

# # 导入相关的方法
# from imblearn.over_sampling import SMOTE
# from imblearn.under_sampling import RandomUnderSampler
# from imblearn.pipeline import Pipeline

# # 划分训练集和测试集
# X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.30)

# #  定义管道
# model = SVC()
# over = SMOTE(sampling_strategy=0.4)
# under = RandomUnderSampler(sampling_strategy=0.5)
# steps = [('o', over), ('u', under), ('model', model)]
# pipeline = Pipeline(steps=steps)

# # 评估效果
# scores = cross_val_score(pipeline, X, y, scoring='roc_auc', cv=5, n_jobs=-1)
# score = mean(scores)
# print('ROC AUC score for the combined sampling method: %.3f' % score)

最佳采样率
在上面的栗子中，我们都是默认经过采样变成50：50，但是这样子的采样比例并非最优选择，因此我们引入一个叫最佳采样率的概念，然后我们通过设置采样的比例，采样网格搜索的方法去找到这个最优点。

# # 导入相关的方法
# from imblearn.over_sampling import SMOTE
# from imblearn.under_sampling import RandomUnderSampler
# from imblearn.pipeline import Pipeline

# # 划分因变量和自变量
# X = df.iloc[:,:-1]
# y = df.iloc[:,-1]

# # values to evaluate
# over_values = [0.3,0.4,0.5]
# under_values = [0.7,0.6,0.5]
# for o in over_values:
#     for u in under_values:
#         # define pipeline
#         model = SVC()
#         over = SMOTE(sampling_strategy=o)
#         under = RandomUnderSampler(sampling_strategy=u)
#         steps = [('over', over), ('under', under), ('model', model)]
#         pipeline = Pipeline(steps=steps)
#         # evaluate pipeline
#         scores = cross_val_score(pipeline, X, y, scoring='roc_auc', cv=5, n_jobs=-1)
#         score = mean(scores)
#         print('SMOTE oversampling rate:%.1f, Random undersampling rate:%.1f , Mean ROC AUC: %.3f' % (o, u, score))

不平衡分类样本若没有经过二次采样平衡样本处理时，则需要注意：

划分数据集时要按类别比例划分训练集和测试集以保持数据分布不变

评估模型时，使用分层k折交叉验证，分层交叉验证中，类别比例在每个分块中得以保持，这使得每个分块中的类别比例与训练数据集的整体比例一致。

# # 把数据分为训练集和测试集(按类别实际分布比例)
# from sklearn.model_selection import train_test_split
# # 提取特征和目标
# features = data_select.drop(['幸存'],axis=1)
# targets = pd.DataFrame(data_select['幸存'])
# # 按照训练集：测试集=7：3比例划分，并且划分后的训练集和测试集的类别分布比例保持一致
# # stratify=targets,用来确保划分后的类别分布比例保持一致
# x_train,x_test,y_train,y_test = train_test_split(features,targets,test_size=0.3,random_state=123,stratify=targets)

# #分层k折交叉验证
# from sklearn.model_selection import StratifiedKFold
#cv=StratifiedKFold(n_splits=5):表示5折分层交叉验证，cv=5:表示5折交叉验证(不考虑类别分布)
# random_cv=RandomizedSearchCV(estimator=model,cv=StratifiedKFold(n_splits=5),random_state=123)

总结各种不平很数据处理方法特点：

随着欠采样程度的加剧，少数类被分对的个数越来越多，分割超平面(图中直线)发生明显变动，但欠采样具有随机性，因此分割超平面的变动一般不会有明显规律；同样地，类加权的处理方法在类别权重改变时，分割超平面也随之变动，但是这种变动不同于欠采样，具有一定的规律：随着少数类权重的增加，分割超平面逐步远离少数类的重心；

以欠采样方式学得的分类器在未来实际测试数据上得到的准确率甚至比在原数据集上训练的分类器准确率还低，这是因为欠采样只是暂时地在训练集上抹去了一部分样本，而实际上分类器未来要预测的还是与原数据分布一致的实例。同样，类加权的处理方法随着少数类的权重逐渐增大，分类准确率也随之下降。但是不平衡学习问题几乎不以准确率作为评价指标，取而代之的往往是少数类的查全率、模型的排序能力等

只要将少数类的权重调得足够大，类加权的处理方法具备使少数类在训练集上的召回率达到100%的潜力，这一点，欠采样是几乎做不到的；但是反过来看，类加权的处理方法是不是更容易学到噪声的特征了呢(导致过拟合)

类的真实比例(数据分布)对于分类新的点非常重要，而这一信息在重新采样数据集时被丢失了。而代价敏感学习不会破坏原始数据的整体分布，因此它也不会丢失类别比例这样的信息

欠采样的比例即使固定，多次实验，结果也未必相同，因为采样具有随机性；但是，类加权的方法只要类别权重固定，结果就不会发生变化。这说明，类加权相较于欠采样，更加稳定

欠采样即便看似有诸多的劣势，但它依然是处理不平衡数据最常用的方法之一。它最大的好处是在处理了类别不平衡的同时，还能减少训练样本，加速模型训练(一天训练5次和一天只能训练一次，明显前者更有潜力获得更好的调参结果)。有人肯定会说，机器学习最重要的是样本量，怎么还能删样本？这样的观点好像总是对的，但是，要知道多数类往往提供的信息都很冗余，这就好比在癌症检测场景中，正常人的各项体征都很近似，导致X变量的分布很集中，重叠度很高。只有癌症患者体征(X)才会差异明显。因此，并不是样本越多越好，而是有价值的样本越多才越好，在癌症这样的场景中，无疑患癌样本(少数类)才最有价值

当我们审视通过代价敏感学习的方法学得的分类器时，我们应清楚地认识到，该分类器是使当前整体样本“代价”最小的分类器，而不是“准确性”最高。如果事实就是少数类比多数类重要100倍，那么在学得的分类器看来，分错99个多数类样本的代价，也没有分错1个少数类的代价高(宁可错杀一百，不可放过一个，如癌症诊断)

3.1.1.2 是否要处理不平衡数据集？

排除数据收集阶段方式因素，不平衡数据本身就蕴含着好坏样本分布的信息，若对不平衡数据做处理使类别平衡，会改变原有数据分布。不平衡数据的处理，肯定要有可解释的场景，能解释通为什么要处理，如果不能回答这个问题，一律建议不处理，尊重事实，保持数据原貌。

此外，只要数据的可分离性好，不管是平衡的还是不平衡的，也不论不平衡性多强，都很容易获得好的结果，甚至不管使用什么方法来处理不平衡数据，结果都会很近似。因此，在实际的数据挖掘任务中，特征发现工程(特征提取/变量挖掘)才是重中之重。

既然每类方法各有优劣，那“我该选择什么方法处理不平衡数据呢？”，下面就以上两类方法，给出一种通用的处理思路：
不论是做机器学习的科研还是企业应用，其中一个重要套路是综合多种方法，来取得一个较优的结果。既然任何一类处理不平衡数据的方法都有其优势与不足，因此，何不同时使用重采样与代价敏感学习呢？这样既可以综合两类方法的优势，还可避免单一方法的不足与偏执。如，先进行一定程度的欠采样，将不平衡性从20:1降至5:1，再进行类加权的代价敏感学习。这里，我给的数据只是随便举例，具体降采样多少(参数1)，类加权的权重如何(参数2)，都可以作为包裹在学习器外的超参数，然后通过诸如网格搜索的方法来寻找二者最优的一组参数值，使得模型效果最理想。

处理不平衡数据的方法很多，要真正了解某个方法，需要在数据集上做一些可视化的实验

每种方法都有自己的优势与不足，为了取得一个较优的结果，可以尝试一种通用的处理策略：综合使用几种熟悉且可靠的方法，并将这些方法的参数作为包裹在学习器之外的超参数

如果要使用重采样的方法，请务必先划分数据集，再在训练集上进行重采样，不然你的测试结果告诉你的都是错误的结论

在实际数据挖掘任务中，获得好的模型的王道还是努力理解业务，发掘有效的独立变量

本例不平衡样本比例为1.6:1，轻度失衡，暂时不做平衡样本处理

data_clean.head()

3.2 异常点数据

异常类型：

异常值
异常样本

存在着一些特别大或者特别小的值，这些可能是离群点或记录错误点，对我们结果会有一些影响的。那我们是需要将离群点数据进行过滤的。

基于统计学的方法

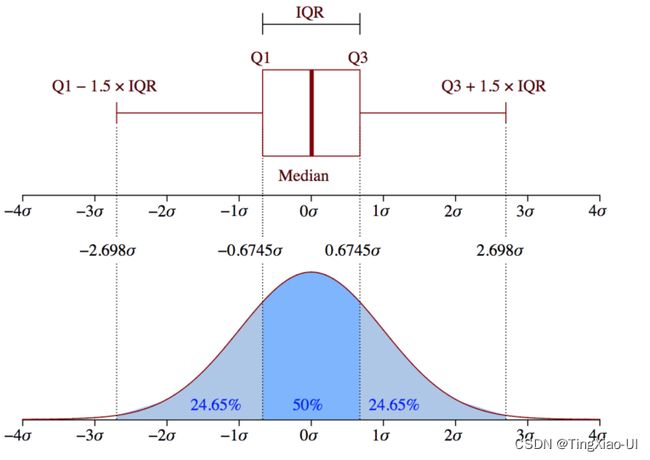
基于百分位数(IQR检测)来筛选异常值点：百分位数度量的是占总数特定百分比的观察点的值。从本质上讲，它们会展示数据集的分布。例如，我们在上面看到的中间数是50百分位数（或p50）。对于中间数（已排好序的数据）来说，50％的值低于它，50％高于它。对于指标而言，百分位数很有意义，因为它们可以清晰地展现数值的分布。

离群点判定

极小的离群点数据：x < (q1 - k * iq)

极大的离群点数据：x > (q3 + k * iq)

Q1 - k * IQR：Q1为序列中25%的中位数，IQR为Q3-Q1

Q3 + k * IQR：Q3为序列中75%的中位数，IQR为Q3-Q1

*当k=1.5时，称为内限，经典的箱线图正是以此为界计算异常值。当k=3时，称为外限。处于内限以外位置的点表示的数据都是异常值，其中在内限与外限之间的异常值为温和的异常值(mild
outliers)，在外限以外的为极端的异常值(extreme outliers)

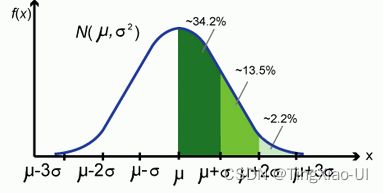
基于高斯分布3σ原则来筛选异常值点：
当取值偏离均值3个标准差的时候，概率较小，认为是异常值点。基于分布算概率的方法要求数据符合特定分布，有一定的局限性

基于百分位数(IQR检测)与3σ原则区别：

IQR检测根据数据的真实分布绘制，他对数据不做任何限制性的要求，比如要服从正态分布等；

IQR检测异常数据识别依赖于上四分数和下四分位数，因此异常值极其偏差不会影响异常值识别的上下边缘。这一点是优于3倍标准差方法的

基于聚类(密度)的方法：半径范围内点的个数即密度

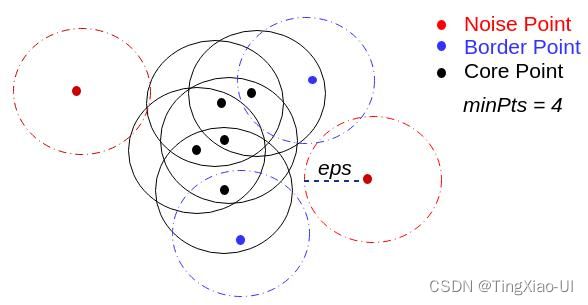
异常点在聚类中表现为单个聚类簇，明显与正常样本区分开。在聚类时同时考虑了多个维度的信息，更适用高纬度的数据。经典的BIRCH和DBSCAN算法都可以在聚类的同时，来识别异常点。DNSCAN算法中异常点示例如下

根据半径、最少点数区分核心点、边界点、噪声点(异常点)

孤立森林(iForest)

适用于连续数据多变量的异常检测,该算法鲁棒性高且对数据集的分布无假设。

孤立森林不需要计算有关距离、密度的指标，可大幅度提升速度，减小系统开销

算法思路：切分样本，知道每一个分割面的样本只有一个。其中密集区域的样本切分次数多，离群点的切分次数相对很少，以此来检测异常点。

想象这样一个场景，我们用一个随机超平面对一个数据空间进行切割，切一次可以生成两个子空间（也可以想象用刀切蛋糕）。接下来，我们再继续随机选取超平面，来切割第一步得到的两个子空间，以此循环下去，直到每子空间里面只包含一个数据点为止。直观上来看，我们可以发现，那些密度很高的簇要被切很多次才会停止切割，即每个点都单独存在于一个子空间内，但那些分布稀疏的点，大都很早就停到一个子空间内了
如下图所示：

上图就是对子样本进行切割训练的过程，左图的 xi 处于密度较高的区域，因此切割了十几次才被分到了单独的子空间，而右图的 x0
落在边缘分布较稀疏的区域，只经历了四次切分就被 “孤立” 了。

下面使孤立森林代码示例

#提取数字特征
data_featrues_num = data_clean.select_dtypes('number')

from sklearn.ensemble import IsolationForest
# 创建模型，n_estimators：int，可选（默认值= 100），集合中的基本估计量(树)的数量
model_isof = IsolationForest(n_estimators=20,random_state=123)
# 计算有无异常的标签分布
outlier_label = model_isof.fit_predict(data_featrues_num)

# 将array 类型的标签数据转成 DataFrame
outlier_pd = pd.DataFrame(outlier_label, columns=['outlier_label'])
# 将标签数据与原来的数据合并
data_merge = pd.concat([data_featrues_num,outlier_pd], axis=1)
data_merge['outlier_label'].value_counts()

附：SKlearn 中其他用于异常检测的方法：

one-class SVM（svm.OneClassSVM）

LocalOutlierFactor（sklearn.neighbors.LocalOutlierFactor）

EllipticEnvelope（covariance.EllipticEnvelope）

3.2.1 异常点数据处理

异常值不代表必须删除！

首先你要明白你的异常检测算法的原理，要明白它是怎么定义异常值的。异常值找到了必须逐项分析它为什么变得异常，找不到原因就必须保留。只有找到了原因并判定确实可以删除你才能删。比如本来是曲线关系，结果你错误删除了你认为的“异常”值，结果真实曲线关系会被你错误拟合为线性关系。如果异常值非常多，一个一个去分析异常原因不太现实，则可以在众多异常值里面随机抽样，抽取少量异常值逐个分析，搞清楚异常的大致规律然后再决定如何处理剩下的异常值。

很多时候真相就在这些异常值里面，慎重删除！

是否要处理异常数据？

检查异常值带有一定主观性，判定没有固定标准，一些异常值也可能同时包含有用的信息，是否需要剔除，应由分析人员自行判断。

异常值一旦处理则无法恢复，建议先备份数据再操作。

如何处理异常数据？

缺失：设置为Null值；此类处理最简单，而且绝大多数情况下均使用此类处理；直接将异常值“干掉”，相当于没有该异常值。如果异常值不多时建议使用此类方法。

填补：如果异常值非常多时，则可能需要进行填补设置，平均值，中位数，众数和随机数、填补数字0共五种填补方式。

不处理：一些异常值也可能同时包含有用的信息，是否需要剔除，应由分析人员自行判断。

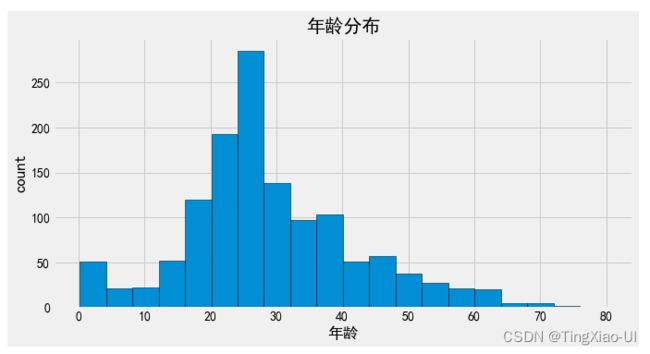
查看年龄分布

fig= plt.figure(figsize=(10,5))
plt.hist(data_clean.年龄,bins=20,edgecolor='k')
plt.xlabel('年龄')
plt.ylabel('count')
plt.title('年龄分布')

查看船票价分布

fig= plt.figure(figsize=(10,5))
ax1=fig.add_subplot(121)
ax1.hist(data_clean.船票价,bins=20,edgecolor='k')
ax1.set_xlabel('船票价')
ax1.set_ylabel('count')
ax1.set_title('船票价分布')

ax2=fig.add_subplot(122)
ax2.hist(data_clean.船票价,bins=20,edgecolor='k')
ax2.set_xlabel('船票价')
ax2.set_ylabel('count')
ax2.set_title('船票价分布')
ax2.set_ylim([0,300])

* 查看异常值数量

q1=data_clean.船票价.describe()['25%']
q3=data_clean.船票价.describe()['75%']
iq=q3-q1

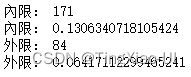
print('內限：',len(data_clean[(data_clean.船票价<(q1-1.5*iq))|(data_clean.船票价>(q3+1.5*iq))]))
print('內限：',len(data_clean[(data_clean.船票价<(q1-1.5*iq))|(data_clean.船票价>(q3+1.5*iq))])/len(data_clean))
print('外限：',len(data_clean[(data_clean.船票价<(q1-1.3*iq))|(data_clean.船票价>(q3+3*iq))]))
print('外限：',len(data_clean[(data_clean.船票价<(q1-1.3*iq))|(data_clean.船票价>(q3+3*iq))])/len(data_clean))

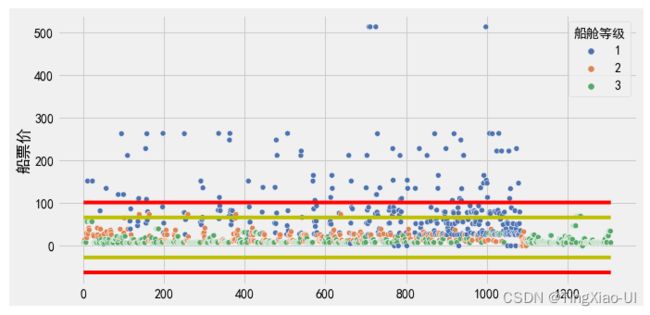
plt.figure(figsize=(10,5))
# plt.scatter(range(len(data_clean)),data_clean['船票价'].values)
sea.scatterplot(data=data_clean,x=range(0,data_clean.shape[0]),y='船票价',hue='船舱等级',palette="deep")
l=len(data_clean)
plt.plot(range(l),[q1-3*iq]*l,'r')
plt.plot(range(l),[q1-1.5*iq]*l,'y')
plt.plot(range(l),[q3+3*iq]*l,'r')
plt.plot(range(l),[q3+1.5*iq]*l,'y')

plt.ylabel('船票价')
# plt.legend(['外限','内限'])

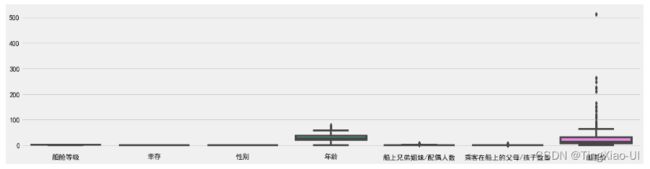
使用箱线图查看单变量异常数据

plt.figure(figsize=(20,5))
sea.boxplot(data=data_clean)

使用孤立森林检测单变量异常点

#使用孤立森林检测单变量异常点
#提取数字特征
data_featrue= pd.concat([data_clean['船票价'],pd.DataFrame(data_clean.index,columns=['index'])],axis=1)
from sklearn.ensemble import IsolationForest
# 创建模型，n_estimators：int，可选（默认值= 100），集合中的基本估计量(树)的数量
model_isof=IsolationForest(n_estimators=500,max_samples=100,contamination='auto',random_state=123)
# model_isof = IsolationForest(n_estimators=100,random_state=123)
# 计算有无异常的标签分布
outlier_label = model_isof.fit_predict(data_featrue)

# 将array 类型的标签数据转成 DataFrame
outlier_pd = pd.DataFrame(outlier_label, columns=['异常'])
# 将标签数据与原来的数据合并
data_merge = pd.concat([data_featrue,outlier_pd], axis=1)
data_merge['异常'].value_counts()#-1代表异常点

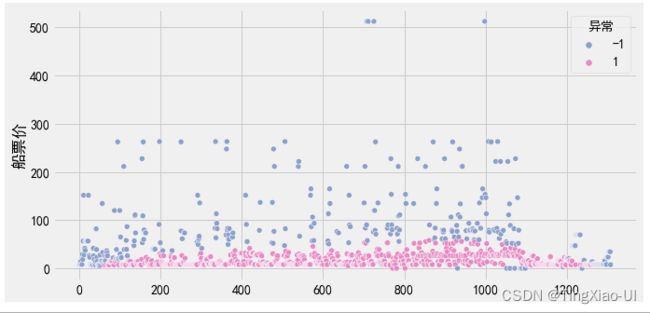
可视化孤立森林

#孤立森林可视化
plt.figure(figsize=(10,5))
sea.scatterplot(data=data_merge, x=range(0,data_merge.shape[0]), y='船票价', hue='异常', palette=sea.color_palette("Set2", 10)[2:4])
l=len(data_clean)
# plt.plot(range(l),[q1-3*iq]*l,'r')
# plt.plot(range(l),[q3+3*iq]*l,'r')
# plt.plot(range(l),[q1-1.5*iq]*l,'y')
# plt.plot(range(l),[q3+1.5*iq]*l,'y')

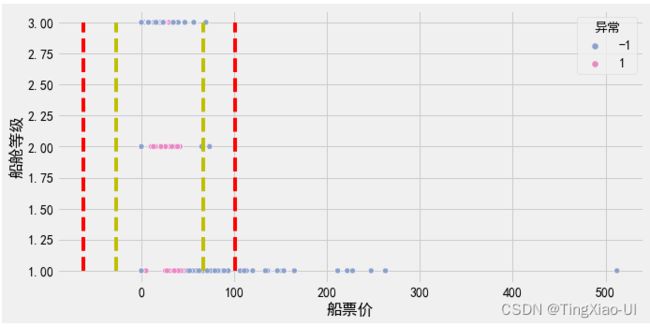
#查看标记为异常的数据的船舱等级情况
plt.figure(figsize=(10,5))
data_plot = data_merge.drop(['index'],axis=1)
data_plot = pd.concat([data_plot,data_clean.船舱等级],axis=1)
sea.scatterplot(data=data_plot,y='船舱等级',x='船票价',hue="异常", palette=sea.color_palette("Set2", 10)[2:4])
l=len(data_clean)
plt.plot([q1-3*iq]*3,range(1,4),'r--')
plt.plot([q3+3*iq]*3,range(1,4),'r--')
plt.plot([q1-1.5*iq]*3,range(1,4),'y--')
plt.plot([q3+1.5*iq]*3,range(1,4),'y--')

#查看标记为异常的数据的生还情况
data_plot = data_merge.drop(['index'],axis=1)
data_plot = pd.concat([data_plot,data_clean.幸存],axis=1)
sea.scatterplot(data=data_plot,y='幸存',x='船票价',hue="异常", palette=sea.color_palette("Set2", 10)[2:4])
l=len(data_clean)
plt.plot([q1-3*iq]*2,range(0,2),'r--')
plt.plot([q3+3*iq]*2,range(0,2),'r--')
plt.plot([q1-1.5*iq]*2,range(0,2),'y--')
plt.plot([q3+1.5*iq]*2,range(0,2),'y--')

)

使用孤立森林检测多变量异常点

#使用孤立森林检测多变量异常点
#提取数字特征
data_featrues_num = data_clean.select_dtypes('number')

from sklearn.ensemble import IsolationForest
# 创建模型，n_estimators：int，可选（默认值= 100），集合中的基本估计量(树)的数量
model_isof=IsolationForest(n_estimators=500,max_samples=100,contamination='auto',random_state=123)
# model_isof = IsolationForest(n_estimators=100,random_state=123)
# 计算有无异常的标签分布
outlier_label = model_isof.fit_predict(data_featrues_num)

# 将array 类型的标签数据转成 DataFrame
outlier_pd = pd.DataFrame(outlier_label, columns=['异常'])
# 将标签数据与原来的数据合并
data_merge = pd.concat([data_featrues_num,outlier_pd], axis=1)
data_merge['异常'].value_counts()
print(data_merge['异常'].value_counts())#-1代表异常点

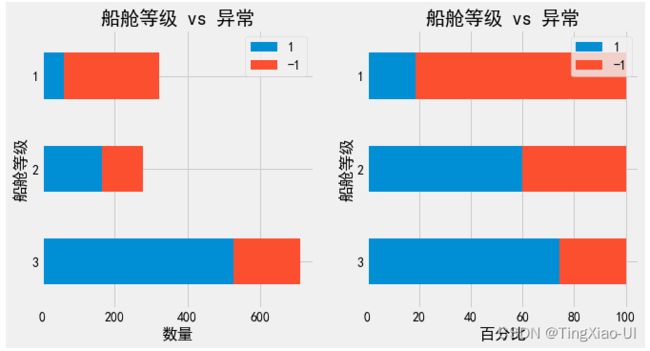
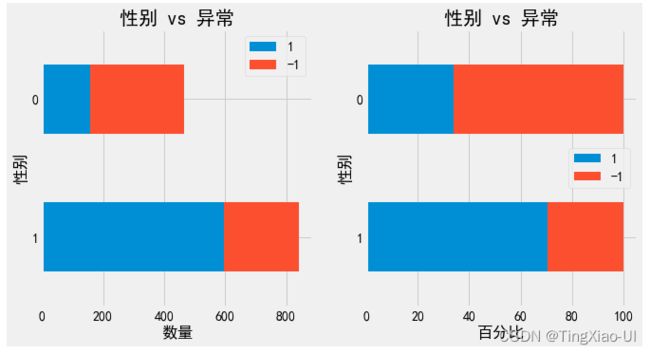
查看异常数据的百分比堆积条形图

barch(data_merge,'船舱等级','异常')

barch(data_merge,'幸存','异常')

barch(data_merge,'性别','异常')

本项目异常点处理

如上图所示两种异常检测方法效果

孤立森林异常检测：随机性较强，且不同船舱等级的票价、年龄的异常点数量占比不同，直接删除会破坏数据原分布，影响模型性能，且无法合理解释异常点存在原因

基于百分位数(IQR检测)异常检测：同样IQR检测出的异常点直接删除也会影响原数据分布，且无法解释异常存在的原因

直接删除异常点会使数据加剧数据不平衡程度

综上，对本项目"异常数据"不做处理

3.3 特征分布

3.3.1 查看不同特征的取值数量

目的：

取值少的可能为类别数据，取值多的为连续型数据
若取值少的数据类型为数值型，可将其分类特征

去重值少的数值型特征可数值分组然后转换为分类特征，即将连续数据离散化(分组、区间化)

连续属性离散化的目的是为了简化数据结构，数据离散化技术可以用来减少给定连续属性值的个数。离散化方法经常作为数据挖掘的工具。

#查看不同特征取值数量
lists_unique=[]
lists_count = []
for j in data_clean.columns:
    lists_unique.append(data_clean[j].nunique())
#     lists_count.append(data_clean[j].count())
    
#unique()：返回去重后的数值
#nunique()：返回各数值的计数
# 取值少的可能为类别性数据，取值多的为连续性数据
#绘制柱状图
plt.figure(figsize=(15,5))
plt.bar(data_clean.columns, [100]*data_clean.shape[1]) # 对每个特征绘制总数状图
plt.bar(data_clean.columns, np.array(lists_unique)/data_clean.shape[0]*100) # 对每个特征绘制去重数柱状图
# plt.plot(range(len(lists)),[100]*len(lists),c='r')
# plt.ylim(0, 100)#设置取值范围

plt.title('特征去重值数量')
plt.xlabel('特征')
plt.ylabel('百分比')
plt.legend(['总数','去重数'])
plt.tight_layout()#防止文字遮挡
plt.show()

查看特征数据

data_clean.select_dtypes('number').head(3)

3.3.2 新增特征

数据离散化

数据离散化(分箱)就是将连续型数据转变成离散型数据。数据离散化是指将连续的数据进行分段，使其变为一段段离散化的区间，离散化的方法可以分为两大类，一种是无监督学习的方式，另一种是有监督学习的方式，分段的原则有基于等距离、等频率、聚类或优化的方法。

为什么要数据离散化？

可以减少过拟合的风险;

增加稀疏数据的概率,减少计算量;

减少噪声数据的影响,比如一组数据按照0~10均匀分布,当数据中突然出现一个500的数据,如果不做离散化的化会对模型的训练造成很大影响；

方便特征衍生,因为数据离散化后就可以把特征直接相互做内积提升特征维度；

离散化后可以提升模型的鲁棒性,比如一组人群数据,其中A:30岁、B:50岁,到了第二年A变成31岁,B变成51岁,理论上要更新模型。但是如果数据离散化了之后,小于40岁为0,大于40岁为1,则第一年和第二年数据没有变化,模型也不用变;

对于分类变量而言，如果类别太多，可能存在个别类别样本量过少，对于数值型变量可能会存在极端值，这都会影响分析的稳健性。这样做可以有助于处理异常值或者样本量较少的值，提高稳定性，并且能够处理与目标变量的非线性关系，从而便于分析，让分析结果或者模型预测更加稳健。

连续数据离散化方法：是否使用标签进行离散化（分箱）决定了有监督还是无监督的离散化方法。有监督的离散化方法又分为建立在错误率基础上的、建立在熵值基础上的或者建立在统计信息基础上的。

有监督分箱：决策树、卡方分箱、生存模型分箱、best_ks、遗传算法分箱等
无监督分箱：等宽、等频、聚类分析等

这类方案的问题在于对于分布不均匀的数据并不适用，等频和等宽都不能很好的反应“尖头”的数据，除非人工手动干涉，聚类本身对于这类问题的表现也并不稳定，经常可能出现的情况就是“尖头”数据有一部分分到平缓分布的数据里去，导致最终的分箱结果没有代表性。

等宽、等频、聚类分析：对不均匀的数据不适用，并且对异常值很敏感，先说等宽分箱，如果数据分布极端，两边数据多，中间数据很少，那么很容易出现不少箱子里面没有数据，等频虽然可以保证每个箱子里的样本数量大致相等，但是有可能出现不同箱子之间跨度太大的情况，比如上述出现异常值的情况，可能最终分箱的结果是一部分箱子的区间长度为10，另一部分箱子的区间长度为1000，同样，对于聚类的方法，不均匀样本和异常样本的存在会导致聚类中心的向极端值偏移从而影响分箱结果

为了克服无监督的离散化方法的这些缺陷，使用类信息来进行离散化的有监督的离散化方法逐渐发展起来。对于分类/回归问题如果要分箱都可以用这种方法，比如下面会提到的动态和静态分箱。

静态分箱：模型训练前的预分箱处理
动态分箱：模型运行的过程中自动完成的，比如决策树实际上在训练的过程中就能够进行自动的分箱操作。

分箱方法

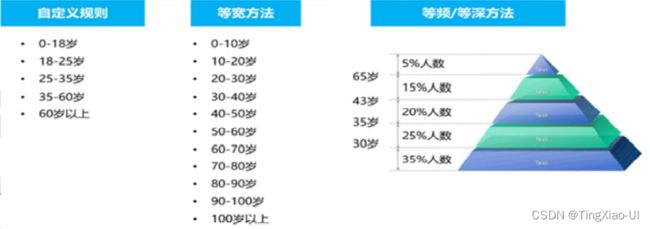
自定义分箱：

等距：等距法也称等宽法，就是变量取值的每个区间的宽度是相等的，即最小值最大值的差值要小于某个数字，这个数字就叫做箱子的宽度。。该等区间法可以较好的保留数据的完整分布性。

等频：就是对于每个箱子中有相同数量的记录数，设为m，则m即为箱子的频率/深度。好处是数据变为均匀分布，但是会更改原有数据的分布状态。简而言之，就是根据数据频率分布去划分数据区间。

基于聚类：组内差异性小，组间差异性大

分位数：利用四分位、五分位、十分位等分位数进行离散。例如：四分位距，是一种衡量一组数据离散程度的统计量，用IQR表示。其值为第一四分位数和第三四分位数的差距。其中 Q1为第一分位数， Q3为第三分位数。

二值化：设定一个阈值，大于阈值为某一固定值，小于阈值则设定为另一固定值，最终得到一个只用于两个值域的二值化数据集

决策树分箱：

卡方分箱

# 自定义数据区间进行划分呢
# pd.cut(df.Q1, bins=[0, 60, 100])# 区间：(0,60],(60,100],(100,]
# 指定分箱数量进行划分
# pd.qcut(df.Q1,q=2)

观察，可对数值型特征如年龄做离散化处理，转换为新分类特征：

幼儿：0-3

儿童：3-6

少年：6-18

青年：18-40

中年：40-65

老年：65-

利用同行的兄弟姐妹或配偶、同行的父母或孩子总数特征创建新特征：是否独自一人
利用同行的兄弟姐妹或配偶、同行的父母或孩子总数特征创建新特征：家庭数量
姓名处理：对姓名作分词处理，观察词频，发现规律：
观察船票号有大量重复值，说明存在多人共用一张船票的情况

根据船票号使用频率，创建新特征：ticket_freq

在创建新特征ticket_freq后，择删除船票号特征

船票价处理：

由于存在多人共用一张船票，单张船票价格也随之增长，而对于使用同一张票的单个乘客，其真实的票价应该除以船票使用人数

船上工作人员应该不用支付船票吧？

年龄分组

变量分组(分箱)有三种类型：◼ 自定义分箱 ◼ 等宽分箱 ◼ 等深分箱/等频分箱

如：对年龄进行分箱操作

年龄自定义分组

#添加新列：age_group,自定义分组
bins = [0,3,6,18,40,65,100]
data_clean['age_group']=pd.cut(data_clean['年龄'],bins,labels=['幼儿','儿童','少年','青年','中年','老年'])
data_clean.head()

新特征：noalone

根据特征：‘船上兄弟姐妹/配偶人数’,'乘客在船上的父母/孩子数量’判断是否独自一人。

data_clean['family_size']=data_clean['船上兄弟姐妹/配偶人数']+data_clean['乘客在船上的父母/孩子数量']+1
data_clean.head()

新特征：ticket_freq

value_freq = pd.DataFrame(data_clean['船票号'].value_counts())
data_ticket = pd.DataFrame({'船票号':data_clean['船票号'].values,'ticket_freq':data_clean['船票号'].values})
#遍历行，填充船票号对应的使用人数
for i in data_ticket.index:
    data_ticket.loc[i,'ticket_freq']=value_freq.loc[data_ticket.loc[i,'船票号'],'船票号']
    
data_ticket=data_ticket.drop(['船票号'],axis=1)#删除船票号列

#data_ticket转换数据类型为float
data_ticket=data_ticket.astype(float)
data_clean=pd.concat([data_clean,data_ticket],axis=1)#合并

#删除船票号特征
data_clean=data_clean.drop(['船票号'],axis=1)

data_clean.head()

姓名处理
- 提取乘客(头衔/称谓)
- 分组

data_clean['title']=data_clean['姓名'].str.extract('([A-Za-z]+)\.')
data_clean['title'].unique()

提取完成之后，对这些称谓进行分类，并用map函数对称谓进行替换。最后，根据提取出的头衔，定义以下身份特征，并对数据集中的头衔进行映射。

data_clean['title'] = data_clean['title'].map({
    'Mr' : 'Man',
    'Master' : 'Man',
    'Miss' : 'Unmarried Woman',
    'Ms' : 'Unmarried Woman',
    'Mlle' : 'Unmarried Woman',
    'Mrs' : 'Married Woman',
    'Lady' : 'Married Woman',
    'Mme' : 'Married Woman',
    'Sir' : 'Nobility' ,
    'Dona' : 'Nobility',
    'Countess' : 'Nobility',
    'Don' : 'Nobility',
    'Jonkheer' : 'Nobility',
    'Rev' : 'Officer',
    'Dr' : 'Officer',
    'Col' : 'Officer',
    'Major' : 'Officer',
    'Capt' : 'Officer'
})

共用船票价格重新计算

# 共用船票价格未重新计算
plt.figure(figsize=(15,5))
plt.subplot(121)
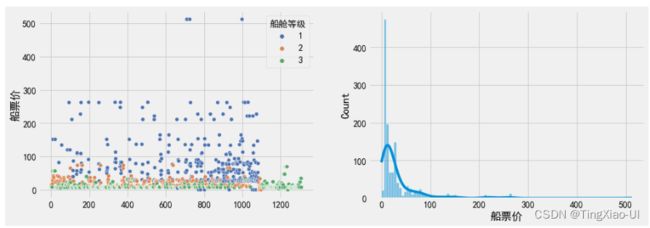
sea.scatterplot(data=data_clean,x=range(0,data_clean.shape[0]),y='船票价',hue='船舱等级',palette="deep")
plt.subplot(122)
sea.histplot(data_clean.船票价,bins=100,kde=True)

#共用船票价重新计算
data_clean['船票价']=data_clean['船票价']/data_clean['ticket_freq']
plt.figure(figsize=(15,5))
plt.subplot(121)
sea.scatterplot(data=data_clean,x=range(0,data_clean.shape[0]),y='船票价',hue='船舱等级',style='幸存',palette="deep")
# plt.ylim([0,15])
plt.subplot(122)
sea.histplot(data_clean.船票价,bins=100,kde=True)

data_clean[data_clean['船票价']<=3][['title','姓名','船舱等级','船票价','age_group','幸存']]

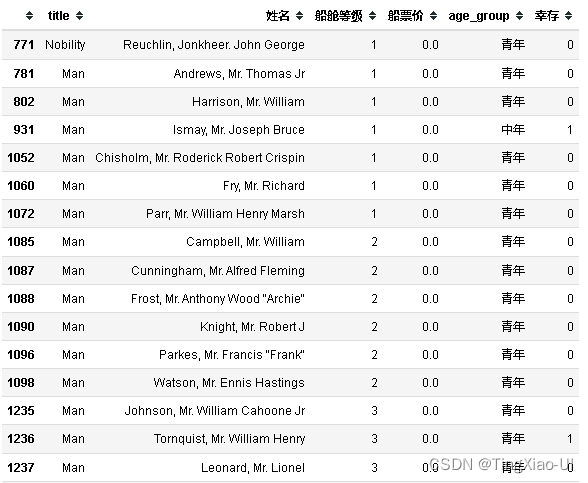
观察，重新计算船票价后，船票价分界线明显。有17位乘客船票价格(船舱等级1、2、3)分布在0元附近，貌似也不是船上工作人员，暂时无法给出票价为0的具体原因。

3.3.3 查看所有特征数据分布

只能显示数值特征分布

tmp = data_clean.select_dtypes('number').drop(['幸存'],axis=1)
cols = tmp.columns # 取得列缩影
plt.figure(figsize=(8, 8))  
for j in range(len(cols)):
    ax = plt.subplot(3,4,j+1)
    ax.set_title(cols[j]) # 设置标题
    sea.histplot(tmp.iloc[:,j],bins=10,kde=True,ax=ax)
    plt.title(j)
    
plt.tight_layout()#防止文字遮挡
plt.show()

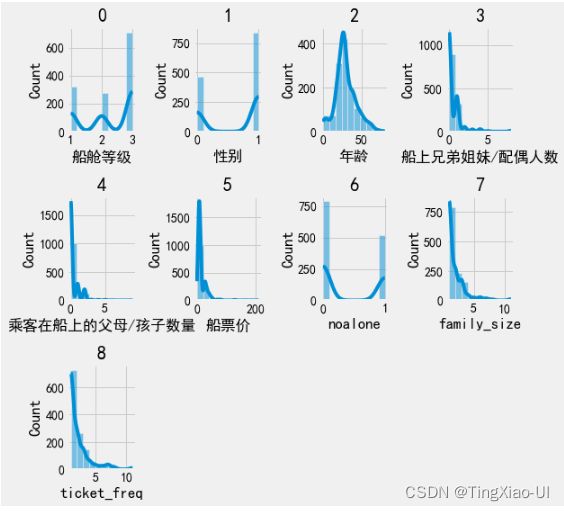
发现有很多特征都是长尾分布的，长尾分布说明特征中少数的数值是离群点数据

3.4 寻找关系

查看分类变量与目标关系

为了查看分类变量对目标的影响，我们可以通过分类变量的值来绘制密度图。
密度图可以显示单个变量的分布，可以认为是平滑的直方图。如果我们通过为分类变量密度曲线着色，这将向我们展示分布如何基于类别变化的。

对于包含较多分类的变量，为了不使图形混乱，可选取数量超过指定阈值的分类来绘图。

查看age_group、性别变量与目标的关系

plt.figure(figsize=(15,5))
#查看age_group分类变量与目标的关系
plt.subplot(1,4,1)
age_list=data_clean.age_group.unique()
for li in age_list:
    subest = data_clean[data_clean.age_group==li]
    sea.kdeplot(data=subest['幸存'])
plt.legend(age_list)
#查看性别变量与目标的关系:{'male':1,'female':0}
plt.subplot(1,4,2)
sex_list=data_clean.性别.unique()
for li in sex_list:
    subest = data_clean[data_clean.性别==li]
    sea.kdeplot(data=subest['幸存'])
plt.legend(['male','female'])
# 查看性别+年龄分类变量与目标的关系
plt.subplot(1,4,3)
for li in age_list:
    subest = data_clean[(data_clean.age_group==li)&(data_clean.性别==1)]
    sea.kdeplot(data=subest['幸存'])
plt.title('male')
plt.legend(age_list)

plt.subplot(1,4,4)
for li in age_list:
    subest = data_clean[(data_clean.age_group==li)&(data_clean.性别==0)]
    sea.kdeplot(data=subest['幸存'])
plt.title('female')
plt.legend(age_list)
#防止文字遮挡
plt.tight_layout()

* 查看船舱等级与目标关系

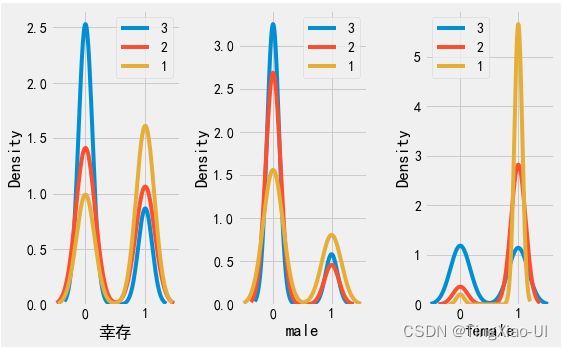
grade_list=data_clean.船舱等级.unique()
plt.figure(figsize=(8,5))
ax = plt.subplot(1,3,1)
for li in grade_list:
    subest = data_clean[data_clean.船舱等级==li]
    sea.kdeplot(data=subest['幸存'],ax=ax)
# ax.set_ylim(0,6)
plt.legend(grade_list)

ax = plt.subplot(1,3,2)
for li in grade_list:
    subest = data_clean[(data_clean.船舱等级==li)&(data_clean.性别==1)]
    sea.kdeplot(data=subest['幸存'],ax=ax)
# ax.set_ylim(0,6)
plt.legend(grade_list)
plt.xlabel('male')

ax = plt.subplot(1,3,3)
for li in grade_list:
    subest = data_clean[(data_clean.船舱等级==li)&(data_clean.性别==0)]
    sea.kdeplot(data=subest['幸存'],ax=ax)
# ax.set_ylim(0,6)
plt.legend(grade_list)
plt.xlabel('female')
plt.tight_layout()#防止文字遮挡

* 查看姓名头衔与目标关系

name_list=data_clean.title.unique()
plt.figure(figsize=(20,5))
ax = plt.subplot(1,3,1)
for li in name_list:
    subest = data_clean[data_clean.title==li]
    sea.kdeplot(data=subest['幸存'],ax=ax)
# ax.set_ylim(0,6)
plt.legend(name_list)

生成堆积百分比条形图-交叉表：crosstab

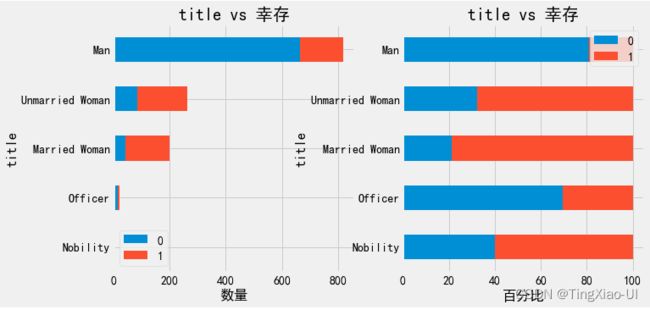
barch(data_clean,'title','船舱等级')

barch(data_clean,'title','幸存')

barch(data_clean[data_clean.title=='Man'],'age_group','幸存')

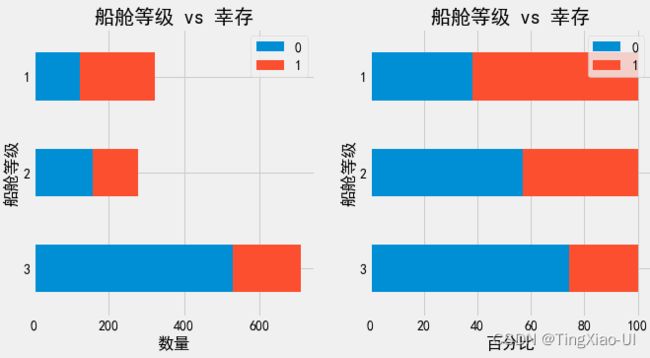
barch(data_clean,'船舱等级','幸存')

乘客生还率随船舱等级逐级下降

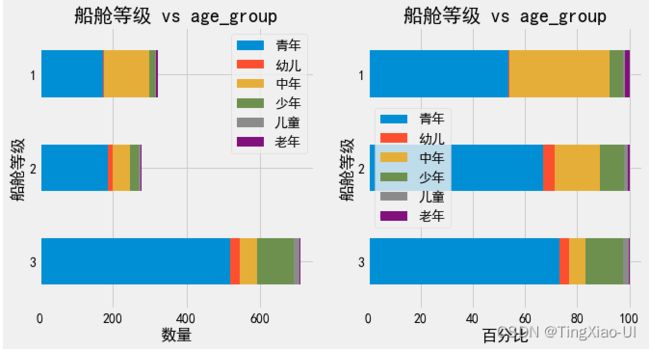
查看不同船舱等级的年龄、性别组成

barch(data_clean,'船舱等级','age_group')

barch(data_clean,'船舱等级','性别')

barch(data_clean,'family_size','幸存')

family_size对乘客生还率有一定的影响，家庭规模越大的乘客生还比例更高，其中family_size=4,5,…,的数量太少，不足以说明问题，不具代表性。

# 绘制百分比堆积条形图
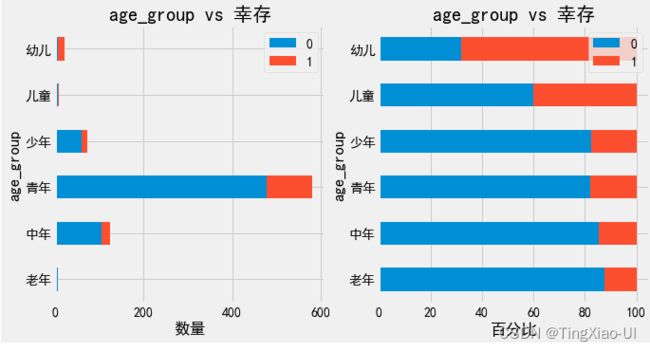
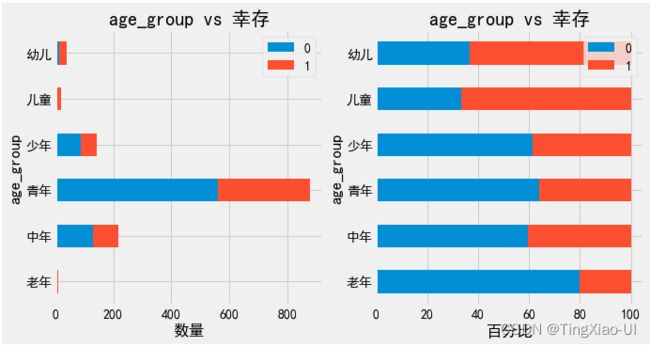
barch(data_clean,'age_group','幸存')

幼儿、儿童生还比例最大

# 绘制百分比堆积条形图
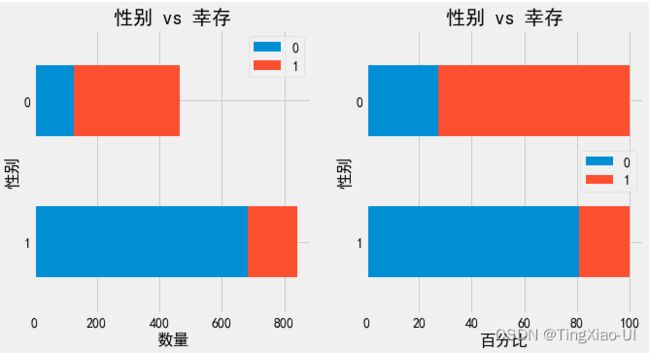
barch(data_clean,'性别','幸存')

女性生还比例最大。

总结：

年龄类型、性别类型对生还率有很大：幼儿、儿童、女性生还几率较大，幼儿、儿童、中年生还率超过40%

船舱等级对应的生还几率随船舱等级逐级下降

乘客中青年、中年比例最多

3.5 特征与目标之间的相关性

为了量化特征（变量）和目标之间的相关性，我们可以计算Pearson相关系数。这是两个变量之间线性关系的强度和方向的度量：

- 1 表示两个变量完全负线性相关，
+1 表示两个变量完全正线性相关。

注意：

特征和目标之间可能存在非线性关系，
相关系数不考虑特征之间的相互作用，

线性关系是开始探索数据趋势的好方法。可以根据这些相关系数值来选择特征用于建模。

计算特征(变量)与目标(幸存)之间的相关系数

#计算特征(变量)与目标(幸存)之间的相关系数并排序
data_corr = data_clean.corr()['幸存'].sort_values()
# 打印相关性
# print(data_corr)
#相关性强度(绝对值)排序:降序
print(data_corr.abs().sort_values(ascending=False))

data_clean.info()

为了考虑可能的非线性关系，我们可以采用特征的平方根和自然对数变换，然后用得分计算相关系数。

为了查看分类特征(age_group、客舱号码、登船的港口)和目标之间任何可能的关系（记住这些是分类变量），我们将对这些列进行one-hot编码。

在下面的代码中，

我们采用数值变量的对数和平方根变换，

对分类变量（age_group、客舱号码、登船的港口）进行one-hot编码，

计算所有特征与得分之间的相关性，

并显示最正和最负相关。

import copy
#提取数字列
number_subset = data_clean.select_dtypes('number')
number_features = number_subset.loc[:,number_subset.columns != '幸存']# 提取特征数据(不包含目标)
# 使用数字列的平方根和对数创建新列
for col in number_features.columns:
    number_features['sqrt_'+col] = np.sqrt(number_features[col])
    number_features['log_'+col] = np.log(number_features[col])
#提取分类列
categorical_features = data_clean[['age_group','客舱号码','登船的港口']]
#对分类变量做one-hot编码
categorical_features=pd.get_dummies(categorical_features)
#使用concat拼接数字特征、分类特征和目标得分
data_select = pd.concat([number_features,categorical_features,data_clean['幸存']],axis=1)
#data_select数据已选出数字特征和one_hot编码后的分类特征
#再次计算data_tmp各变量与目标(幸存)的相关性
tiger_corr = data_select.corr()['幸存']

data_clean.select_dtypes('number').corr().abs()['幸存'].sort_values(ascending=False).head(50)

添加对数特征、平方根特征后：

最强的关系仍然性别、其次是船舱等级。

对数和平方根变换似乎没有导致任何更强的关系。

对分类变量one_hot编码后，‘age_group’,‘客舱号码’,'登船的港口’与目标正相关，但没有强烈的正线性关系。

我们可以使用这些相关性来执行特征选择。

现在，让我们绘制数据集中最重要的相关性(绝对值)，即性别，船舱等级。我们可以按照分类特征类型为图表着色，以显示它如何影响关系。

3.6 双变量图

为了可视化两个变量之间的关系，我们使用散点图。我们还可以使用诸如标记的颜色或标记的大小等方面包括其他变量。在这里，我们将相互绘制两个数字变量，并使用颜色表示第三个分类变量。

data_plot = copy.deepcopy(data_clean)
#绘制散点图
sea.lmplot(data=data_plot,x='年龄',y='船舱等级',hue='性别',fit_reg = False)
plt.xlabel('年龄')
plt.ylabel('船舱等级')
plt.title('年龄vs 船舱等级')

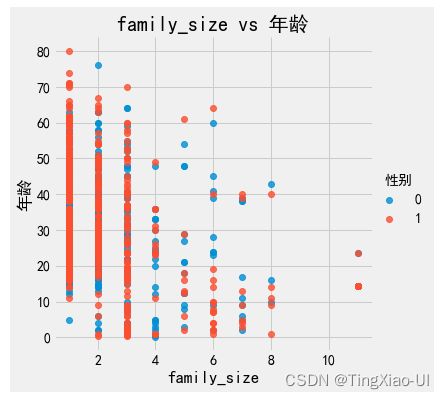
sea.lmplot(data=data_plot,x='family_size',y='年龄',hue='性别',fit_reg = False)
plt.xlabel('family_size')
plt.ylabel('年龄')
plt.title('family_size vs 年龄')

plt.figure(figsize=(15,5))
ax = plt.subplot(1,3,1)
sea.kdeplot(data=data_clean, x="年龄", y="船票价", hue="幸存",fill=False,alpha=1,shade_lowest=False)
ax = plt.subplot(1,3,2)
sea.kdeplot(data=data_clean[data_clean.幸存==1], x="年龄", y="船票价",color='r')
ax = plt.subplot(1,3,3)
sea.kdeplot(data=data_clean[data_clean.幸存==0], x="年龄", y="船票价",color='b')

船票价、年龄与乘客生还率集中趋势并没有明显区别。

猜测，灾难发生时，游轮并不是立即沉没，乘客有一定自救时间且现场有人员维护秩序，乘客生还影响因素应该考虑现场管理人员如船员的管理能力、船员人数、救生艇数量即承载能力。

3.6.1 查看特征与特征、与目标的相关性

作为探索性数据分析的最后一个练习，我们可以在几个不同的变量之间建立Pairs Plot。 Pairs Plot是一次检查多个变量的好方法，因为它显示了对角线上的变量对和单个变量直方图之间的散点图。

#提取要绘制的列
col=['船舱等级','年龄','船票价','noalone','family_size','ticket_freq','幸存']
data_plot = data_select[col]
#inf 替换为NaN
data_plot=data_plot.replace({np.inf:np.nan,-np.inf:np.nan})
# #过滤NaN值
data_plot = data_plot.dropna()

#查看变量间的关系图
sea.pairplot(data_plot)
plt.tight_layout()  # 防止文字遮挡

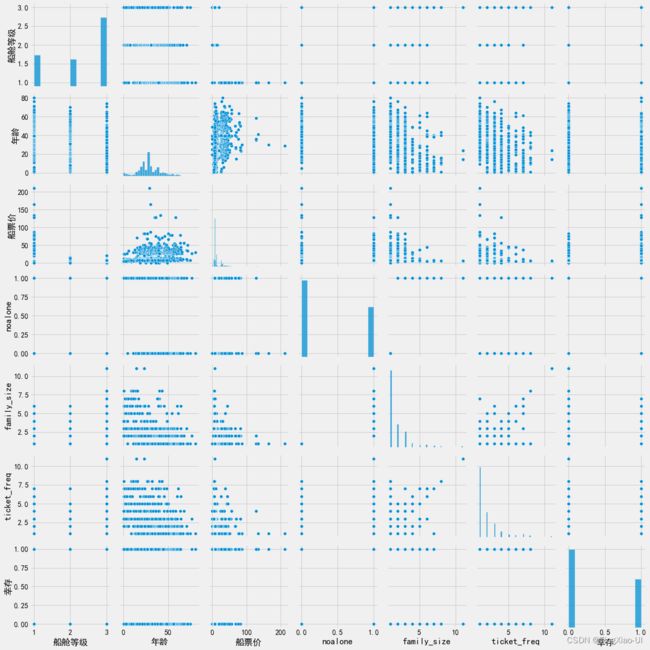
使用parigrid对象绘制变量成对关系图
使用seaborn PairGrid函数，我们可以将不同的图绘制到网格的三个方面:

上三角显示散点图

对角线将显示直方图

下三角形将显示两个变量之间的相关系数和两个变量的2-D核密度估计。

# 计算某两列之间的相关系数
def corr_func(x,y,**kwargs):
    r = np.corrcoef(x,y)[0][1]
    ax = plt.gca()
    ax.annotate("r = {:.2f}".format(r),
                xy = (.2,.8),
                xycoords = ax.transAxes,
                size = 20)

grid= sea.PairGrid(data_plot)
# 在对角线上的坐标轴内画图
grid.map_diag(sea.histplot)
# 在非对角线上的坐标轴内画图
# grid.map_offdiag(sea.kdeplot, n_levels=6)
#在上三角绘制散点图
grid.map_upper(sea.scatterplot)
# 在下三角绘制核密度图+相关系数
grid.map_lower(sea.kdeplot,cmap = plt.cm.Reds)
grid.map_lower(corr_func)

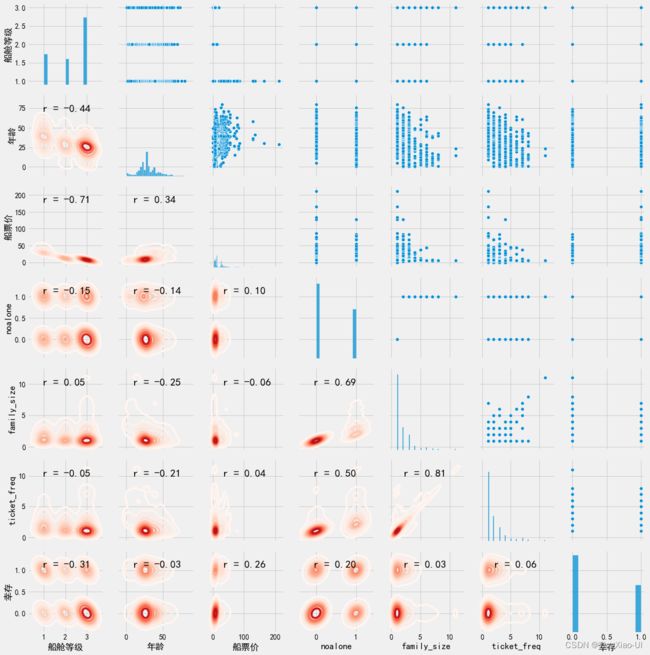
通过PairGrid图我们可以看到特征之间、特征与目标之间的关系图，通过添加更多的特征变量，可以观察到哪些特征是共线特征(冗余特征)，哪些是无关特征。

4. 特征工程

现在我们已经台探索了数据中的趋势和关系，我们可以使用EDA的结果来构建特征工程。我们从EDA学到了以下知识，可以帮助我们进行特征工程：
问题类型：分类、监督学习问题，

目标字段：幸存；新增字段：age_group,noalone,family_size,ticket_freq；删除字段：body(泄露目标信息)、船票号(待创建ticket_freq特征后删除)、救生艇

数据没有重复样本：注意要删除列之前做重复样本处理，因为提前删除列的化可能会把唯一表示删除，导致删除列后的数据有重复样本(事实上不重复)

姓名字段可能包含性别、国籍、种族等信息待分析处理，暂时按照头衔分组处理

船舱等级、noalone应为分类特征，需转换数据类型分类字段

保留"异常数据"，不做处理

数据轻度偏斜，不做二次采样处理

分类特征：性别、age_group、船舱等级对乘客生还率有重大影响，家庭规模对于幼儿、儿童的生还率有一定影响

数字特征：部分对数特征可以一定程度提高特征与目标之间的相关性，即特征与目标之间可能存下非线性关系

保留特征：

数字特征：年龄、船上兄弟姐妹/配偶人数、乘客在船上的父母/孩子数量、船票价，family_size，ticket_freq，对数列；

分类特征：船舱等级，性别、姓名、客舱号码、登陆的港口，age_group,noalone；

猜测，灾难发生时，游轮并不是立即沉没，乘客有一定自救时间且现场有人员维护秩序，乘客生还影响因素应该考虑现场管理人员如船员的管理能力、船员人数、救生艇数量即其承载能力。

在我们进一步讨论之前，我们应该定义什么是特征工程：数据预处理+特征选择+特征缩减

获取原始数据并提取或创建新特征的过程。这可能意味着需要对变量进行变换，例如对数和平方根，或者对分类变量进行one-hot编码，以便它们可以在模型中使用。
一般来说，我认为特征工程是从原始数据创建附加特征。

选择数据中最相关的特征的过程。在特征选择中，我们删除特征以帮助模型更好地总结新数据并创建更具可解释性的模型。一般来说，特征选择是减去特征，所以我们只留下那些最重要的特征。

在此项目中，我们将采用以下步骤进行特征工程：

数据预处理：转换数据类型、过滤缺失值占比超过阈值的列

新增特征：划分数据集、填充完缺失值后才能新增

对数特征、family_size、ticket_freq、age_group、noalone

删除特征：

body、船票号、救生艇列

提取特征：

数字特征：年龄、船上兄弟姐妹/配偶人数、乘客在船上的父母/孩子数量、船票价，family_size，ticket_freq，对数列

分类特征：船舱等级，性别、title、客舱号码、登陆的港口，age_group,noalone

分割数据集：按类别比例划分

训练集

缺失值

填充缺失值：

填充数字特征

填充分类特征

特征缩放

分类特征做one_hot编码

特征选择：保留有价值特征，删除无关特征和冗余特征(共线特征)

为避免数据泄露(训练集和测试集交叉污染)问题，需要注意特征工程的部分操作顺序

数据分割前的特征工程

转换数据为正确类型(字符串数字转为数字)、过滤重复值、过滤异常值、删除缺失值占比大于指定阈值的特征 *
提取特征(数字特征+指定的分类特征)，添加数字特征的数学变换列、分类特征做one-hot编码 *
特征选择：过滤特征值均为NaN的特征(做数学变换后，容易产生值均为NaN的列)、过滤冗余特征(大于指定相关系数的特征)

数据分割：训练集+测试集
数据分割后的特征工程

分别对训练集和测试集填充缺失值

分别对训练集和测试集做特征缩放

4.1 数据预处理

# 重命名
data_raw = data_raw.rename(columns={'船上兄弟姐妹/配偶人数':'sibsp','乘客在船上的父母/孩子数量':'parch'})
#复制数据
data_clean = copy.deepcopy(data_raw)

处理重复样本

查看重复值

data_clean.duplicated().value_counts()

无重复样本，此时可以删除EDA时不需要的列：body,注意要删除列之前做重复样本处理，因为提前删除列的化可能会把唯一表示删除，导致删除列后的数据有重复样本(事实上不重复)。

#删除body、救生艇列
data_clean = data_clean.drop(['body','救生艇'],axis=1)
# 船票号特征这一步暂时不删除,待新增完ticket_freq列后删除

4.1.2将数据转换为正确类型

object类型：object数据类型是dataframe中特殊的数据类型,当某一列出现数字、字符串、特殊字符和时间格式两种及以上时,就会出现object类型,即便把不同类型的拆分开,仍然是object类型

查看数据类型

data_clean.info()

from pandas.api.types import CategoricalDtype
#提取类别
grade_list = data_clean['船舱等级'].dropna().unique()#注意要过滤缺失值
sex_list = data_clean['性别'].dropna().unique()
port_list = data_clean['登船的港口'].dropna().unique()
#转换类型
cat_dtype_grade=CategoricalDtype(categories=grade_list,ordered=True)#ordered:是否为定序类别
cat_dtype_sex=CategoricalDtype(categories=sex_list,ordered=False)#ordered:是否为定序类别
cat_dtype_port=CategoricalDtype(categories=port_list,ordered=False)#ordered:是否为定序类别
data_clean['船舱等级']=data_clean['船舱等级'].astype(cat_dtype_grade)
data_clean['性别']=data_clean['性别'].astype(cat_dtype_sex)
data_clean['登船的港口']=data_clean['登船的港口'].astype(cat_dtype_port)

data_clean.info()

处理客舱号码字段

提取客舱号码字段的舱位号

根据船票号填充缺失项的舱位号

查看此时客舱号码缺失比例，若缺失比例依然很大，则缺失值替换为字母’U’（unknown）

def missing_values_table(df):
    #计算总的缺失值数量并降序处理
    mis_val = df.isnull().sum().sort_values(ascending=False)
    mis_val = mis_val[mis_val>0]#提取有缺失值的列
    #计算缺失值比例
    percent = round(mis_val* 100 /len(df),2)
    mis_val_table_ren_columns=pd.concat([mis_val,percent], axis=1, keys=['Missing Values','Percent'])
    #打印总结信息：总的列数，有数据缺失的列数
    print ("数据集共有 " + str(df.shape[1]) + " 列.\n"+"其中 " + str(mis_val_table_ren_columns.shape[0]) +
              " 列有缺失值")
    # 返回带有缺失值信息的dataframe
    return mis_val_table_ren_columns
missing_values_table(data_clean)

# #提取字符
# import re
# # grade_num = data_clean.dropna(subset=['客舱号码']).loc[:,['船舱等级','客舱号码']]
# grade_num = data_clean.loc[:,['船舱等级','客舱号码']]

# for i in grade_num.dropna(subset=['客舱号码']).index:
#     strs = list(set(re.findall('[a-zA-Z]+',grade_num.loc[i,'客舱号码'])))
#     if len(set(strs))>1:
#         strs = ''.join(strs)
#     else:
#         strs = strs[0]
#     data_clean.loc[i,'客舱号码'] = strs

# null_lists = data_clean[pd.isnull(data_clean.客舱号码)].index
# # tmp = data_clean[['船票号','客舱号码']]
# for i in  null_lists:
#     ticket_num = data_clean.loc[i,'船票号']
#     cabin_lists = set(list(data_clean[data_clean.船票号==ticket_num].客舱号码.dropna()))
#     if len(cabin_lists)>0:
# #         print(cabin_lists)
#         data_clean.loc[i,'客舱号码']=cabin_lists

# missing_values_table(data_clean) 

# data_clean.客舱号码=data_clean.客舱号码.fillna(value='U')
# missing_values_table(data_clean)

# cat_dtype_port=CategoricalDtype(categories=data_clean.客舱号码.unique().tolist(),ordered=False)#ordered:是否为定序类别
# data_clean['客舱号码']=data_clean['客舱号码'].astype(cat_dtype_port)

4.1.3 过滤缺失值超过阈值的列

将含大量缺失值的列：客舱号码直接删除，其余缺失项待划分数据集后，做填充处理

 missing_values_table(data_clean)

data_clean = data_clean.drop(['客舱号码'],axis=1)
data_clean.head()

4.1.4 分类特征做one_hot编码

查看分类特征缺失值情况

missing_values_table(data_clean.select_dtypes('category'))

注意分类特征含缺失值，此时为分类特征做one_hot编码会自动过滤分类特征中的缺失值，需填充完缺失值后才能编码。所以为分类特征做one_hot编码需留在划分数据集、填充缺失值后进行。

4.1.5 提取数字特征和分类特征

data_clean.info()

# 创造新列：
#对数列，平方根列，age_group,noalone,family_size,ticket_freq 待填充完缺失值后再创建
# 提取数字特征(不包括目标列)
number_subset = data_clean.select_dtypes('number')
number_features = number_subset.loc[:,number_subset.columns!='幸存']

#提取分类列
# categorical_features = data_clean[['Borough','Largest Property Use Type']]
categorical_features = data_clean.select_dtypes('category')
#注意船票号
categorical_features = pd.concat([categorical_features,data_clean.船票号,data_clean.姓名],axis=1)

#组合特征
features = pd.concat([number_features,categorical_features],axis=1)
data_select = pd.concat([features,data_clean['幸存']],axis=1)

data_select.head()

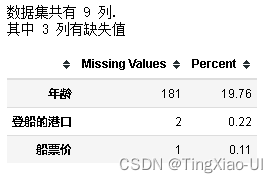
missing_values_table(data_select)

4.2 划分数据集为训练集+测试集

需要将原始的数据集分成训练数据集和测试数据集，训练集用来训练模型，测试集用来评估模型性能和泛化能力。

4.2.1 打乱数据

原始的数据，样本可能是按照某种顺序进行排列，如前半部分为某一类别的数据，后半部分为另一类别的数据。但经过打乱之后数据的排列就会拥有一定的随机性，在顺序读取的时候下一次得到的样本为任何一类型的数据的可能性相同。，打乱数据之间的顺序，让数据随机化，这样可以避免过拟合。

打乱全量数据：极端情况就是训练数据跟测试数据完全不一样，这样训练数据上学到的模型就很难用于预测测试数据了，所以为了避免这种情况，需要在划分数据集前打乱全量数据。

对于那种对随机性比较敏感的模型，典型的就是神经网络，打乱数据很重要。由于NN参数多，学习能力强，所以就对数据的 randomness 要求比较高。而且假设送进去的数据是按照某个规律去排列的，这个规律本身极大可能也会被NN学习到，但这个规律是一个本来不应该被学到的规律，模型中包含这个顺序的规律会干扰后来的预测。

对于那种对随机性不太敏感的模型，理论上说可以不打乱。但敏感不敏感也跟数据量级，复杂度，算法内部计算机制都有关，目前并没有一个经纬分明的算法随机度敏感度列表。既然打乱数据并不会得到一个更差的结果，一般推荐的做法就是打乱全量数据。

sklearn.model_selection.train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)

shuffle:表示打乱数据集后再划分数据集，默认True

stratify:表示是否以分层方式拆分数据，并将其用作类标签，默认None

对于分类问题，注意要按照类别比例划分数据集，即划分前后的数据集的类别分布保持不变

# 把数据分为训练集和测试集
from sklearn.model_selection import train_test_split

# 提取特征和目标
features = data_select.drop(['幸存'],axis=1)
targets = pd.DataFrame(data_select['幸存'])

# 按照7：3比例划分，并且划分后的类别分布比例保持一致
# stratify=targets,用来确保划分后的类别分布比例保持一致
x_train,x_test,y_train,y_test = train_test_split(features,targets,test_size=0.3,random_state=123,shuffle=True,stratify=targets)
#查看训练集、测试集的目标类别划分比例
print(y_train.value_counts()[0]/y_train.value_counts()[1])
print(y_test.value_counts()[0]/y_test.value_counts()[1])

print('训练集:',x_train.shape,'测试集:',x_test.shape)

4.3 填充缺失值

分别对划分后的训练集和测试集填充缺失值以防数据泄露
训练集和测试集填充完缺失值后再添加新列：对数列，age_group,noalone,family_size,ticket_freq

missing_values_table(x_train)

missing_values_table(x_test)

4.3.1 填充缺失值

填充年龄字段缺失值
训练集填充

groups = x_train.groupby(['性别','船舱等级']).mean()#填充均值
for i in x_train['年龄'].index:
    if pd.isnull(x_train['年龄'][i]):
        value_age = groups.loc[x_train['性别'][i],:].loc[x_train['船舱等级'][i],'年龄']
        x_train.loc[i,'年龄']= value_age

测试集填充

groups = x_test.groupby(['性别','船舱等级']).mean()#填充均值
for i in x_test['年龄'].index:
    if pd.isnull(x_test['年龄'][i]):
        value_age = groups.loc[x_test['性别'][i],:].loc[x_test['船舱等级'][i],'年龄']
        x_test.loc[i,'年龄']= value_age

船票价填充

EDA过程中发现：船票价字段与船舱等级关联度最高，其次是幸存；由于只缺失一个数值，即没有连片缺失，所以这里采用KNN填充，根据船舱等级、年龄字段判断距离最近，寻找即最相似的的乘客对应的票价。

填充训练集

def KNNImputerNum(inx,k=1):
    #inx = data_clean[['Latitude','Longitude','Borough']]
    result = copy.deepcopy(inx)
    base = copy.deepcopy(inx.iloc[:,:-1])
    col = list(result.columns)[-1]
    for row in result.index:
        if pd.isnull(result.loc[row,col]):
            #计算距离
            dis = np.linalg.norm((base-base.loc[row,:]),axis=1)
            index = dis.argsort()[k]
            while pd.isnull(inx.iloc[index,-1]) and k<dis.shape[0]:
                k+=1
                index = dis.argsort()[k]
            if k<dis.shape[0]:
                #填充缺失值
                result.loc[row,col]=inx.iloc[index,-1]
            else:
                print('无法填充，该'+col+'整列缺失！')
                return
    return result

tmp =copy.deepcopy(x_train[['船舱等级','年龄','船票价']])
# 将tmp['船舱等级']分类特征转换为数值型特征
tmp['船舱等级']=tmp['船舱等级'].astype(int)
x_train[['船舱等级','年龄','船票价']]=KNNImputerNum(tmp,k=1)
# 将x_train['船舱等级']转换为正确类型：分类特征
cat_dtype_grade=CategoricalDtype(categories=[1,2,3],ordered=True)#ordered:是否为定序类别
x_train['船舱等级']=x_train['船舱等级'].astype(cat_dtype_grade)

x_train.info()

3. 登船的港口填充缺失值：仅训练集有缺失

登船的港口字段为分类特征，缺失值较少，采用填充众数的方式

#使用港口的众数填充缺失值
value_mode = x_train.登船的港口.dropna().mode()[0]
x_train.登船的港口=x_train.登船的港口.fillna(value=value_mode)

查看训练集、测试集缺失情况

missing_values_table(x_train)

missing_values_table(x_test)

4.3.2 新增特征

数值特征：对数列，family_size,ticket_freq
分类特征：title,age_group,noalone

为方便操作，先将训练集、测试集合并，新增完特征后再按原有顺序拆分。

#组合训练集和测试集
features = pd.concat([x_train,x_test],axis=0)
targets = pd.concat([y_train,y_test],axis=0)
# x_train = features.iloc[:x_train.shape[0],:]
# x_test = features.iloc[x_train.shape[0]:,:]
features.shape

新增对数特征

# 提取数字特征(不包括目标列)
number_features = features.select_dtypes('number')

# 创建新列:注意取对数后可能会得到无穷大值,以及NAN
for col in number_features.columns:
    number_features['log_'+col] = np.log(number_features[col])#对数
#     number_features['sqrt_'+col] = np.sqrt(number_features[col])#平方
#替换np.inf为np.nan
number_features = number_features.replace({np.inf:np.nan,-np.inf:np.nan})

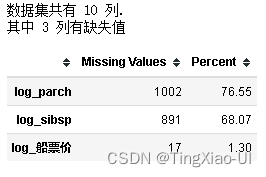
查看新增对数列、平方根列后数据缺失情况

missing_values_table(number_features)

删除log_parch、log_sibsp列

number_features=number_features.drop(['log_parch','log_sibsp'],axis=1)
missing_values_table(number_features)

新增family_size特征

number_features['family_size']=number_features['sibsp']+number_features['parch']+1
missing_values_table(number_features)

新增ticket_freq特征

#提取分类列
categorical_features = features.select_dtypes('category')
categorical_features=pd.concat([categorical_features,features.船票号,features.姓名],axis=1)
categorical_features.head(3)

value_freq = pd.DataFrame(categorical_features['船票号'].value_counts())
data_ticket = pd.DataFrame({'船票号':categorical_features['船票号'].values,'ticket_freq':0})
#遍历行，填充船票号对应的使用人数
for i in data_ticket.index:
    try:
        data_ticket.loc[i,'ticket_freq']=value_freq.loc[data_ticket.loc[i,'船票号'],'船票号']
    except:
        print('1:',data_ticket.loc[i,'ticket_freq'],i)
        print('2:',value_freq.loc[data_ticket.loc[i,'船票号'],'船票号'])
    
data_ticket=data_ticket.drop(['船票号'],axis=1)#删除船票号列
data_ticket.info()

#data_ticket转换数据类型为float
data_ticket=data_ticket.astype(float)
categorical_features=categorical_features.drop(['船票号'],axis=1)#删除船票号列
number_features=pd.concat([number_features,data_ticket],axis=1)#合并

共用船票价重新计算

#共用船票价重新计算
number_features['船票价']=number_features['船票价']/number_features['ticket_freq']

新增age_group特征:将连续型数据age离散化(分组)

#添加新列：age_group
bins = [0,3,6,18,40,65,100]
categorical_features['age_group']=pd.cut(number_features['年龄'], bins,labels=['幼儿','儿童','少年','青年','中年','老年'])
categorical_features.head()

categorical_features.info()

新增noalone特征

categorical_features['noalone']=features[['sibsp','parch']].apply(lambda x: 1 if x.sum()>0 else 0, axis=1)
categorical_features.info()

noalone_list=categorical_features['noalone'].unique().tolist()
#转换数据类型为分类特征
cat_dtype_grade=CategoricalDtype(categories=noalone_list,ordered=False)#ordered:是否为定序类别
categorical_features['noalone']=categorical_features['noalone'].astype(cat_dtype_grade)
categorical_features.info()

新增名字分组特征：title

categorical_features['title']=categorical_features['姓名'].str.extract('([A-Za-z]+)\.')
categorical_features['title'] = categorical_features['title'].map({
    'Mr' : 'Man',
    'Master' : 'Man',
    'Miss' : 'Unmarried Woman',
    'Ms' : 'Unmarried Woman',
    'Mlle' : 'Unmarried Woman',
    'Mrs' : 'Married Woman',
    'Lady' : 'Married Woman',
    'Mme' : 'Married Woman',
    'Sir' : 'Nobility' ,
    'Dona' : 'Nobility',
    'Countess' : 'Nobility',
    'Don' : 'Nobility',
    'Jonkheer' : 'Nobility',
    'Rev' : 'Officer',
    'Dr' : 'Officer',
    'Col' : 'Officer',
    'Major' : 'Officer',
    'Capt' : 'Officer'
})
categorical_features=categorical_features.drop(['姓名'],axis=1)
categorical_features.info()

title_list=categorical_features['title'].unique().tolist()
#转换数据类型为分类特征
cat_dtype_grade=CategoricalDtype(categories=title_list,ordered=False)#ordered:是否为定序类别
categorical_features['title']=categorical_features['title'].astype(cat_dtype_grade)
categorical_features.info()

合并特征，并按照索引拆分特征为训练集和测试集

features = pd.concat([number_features,categorical_features],axis=1)
x_train = features.iloc[:x_train.shape[0],:]
x_test = features.iloc[x_train.shape[0]:,:]
features.info()

missing_values_table(x_train)

#使用均值填充缺失值
value_mean = x_train['log_船票价'].dropna().mean()
x_train.loc[:,'log_船票价']=x_train.loc[:,'log_船票价'].fillna(value=value_mean)

missing_values_table(x_test)

#使用均值填充缺失值
value_mean = x_test['log_船票价'].dropna().mean()
x_test.loc[:,'log_船票价']=x_test.loc[:,'log_船票价'].fillna(value=value_mean)

4.4 特征缩放

特征具有不同的单位，我们希望对特征进行标准化，以使特征单位不影响算法。

在重复值、缺失值、异常值、分割数据(训练集和测试集)之后，特征选择、建模之前，做特征缩放

注意要在分割数据后，分别对训练集和测试集做特征缩放，而不是分割数据之前做特征缩放，否则会导致训练集和测试集失去独立性，使得训练集和测试集的交叉污染产生数据泄露现象。

若把训练集和测试集合在一起做归一化，这样特征范围就统一了。之后用训练集做训练，那测试集做测试。但很明显的，在训练模型时，不应该包括任何测试集的信息。这种做法会导致存在人为偏差的模型，不能用。

使用自定义归一化函数做特征缩放

def scalerMm(inx,model='min'):#inx:特征类型为数值特征和category特征两种
    base = copy.deepcopy(inx)
    for col in base.columns:
        #排除非数值类型的列
        if str(base[col].dtypes) != 'category' and str(base[col].dtypes) != 'object':
#             print(col,base[col].dtypes)
            value_max = np.max(base[col])
            value_min = np.min(base[col])
            scale = value_max-value_min
            if model=='min':
                base[col] = (base[col]-value_min)/scale
            elif model=='mean':
                value_mean = np.mean(base[col])
                base[col] = (base[col]-value_mean)/scale
    #             print(value_mean)
    return base

#1. 训练集做特征缩放
x_train = scalerMm(x_train)#DataFrame,m*n
#2. 测试集做特征缩放
x_test = scalerMm(x_test)#DataFrame,m*n

4.5 分类特征做one_hot编码

注意需要组合训练集和测试集后做对其分类特征做one_hot编码
例如：训练集x_train[col]有类别a1,而测试集x_test[col]没有类别a1,若分开做one_hot编码，会导致训练集和测试集的维度不一致。

#组合训练集和测试集
features = pd.concat([x_train,x_test],axis=0)
targets = pd.concat([y_train,y_test],axis=0)
# x_train = features.iloc[:x_train.shape[0],:]
# x_test = features.iloc[x_train.shape[0]:,:]
features.shape

# 提取数字特征(不包括目标列)
number_features = features.select_dtypes('number')
#提取分类列
categorical_features = features.select_dtypes('category')
#对分类变量做one-hot编码
categorical_features=pd.get_dummies(categorical_features)
#组合特征
features = pd.concat([number_features,categorical_features],axis=1)

# x_train = features.iloc[:x_train.shape[0],:]
# x_test = features.iloc[x_train.shape[0]:,:]

4.6 特征选择

为了在特征选择处理后，训练集和测试集的维度、属性一致，需先将训练集和测试集组合后再做特征选择，然后再拆分,由于上一步已做组合处理，这里就不在重复。

4.6.1查看特征与特征的相关性

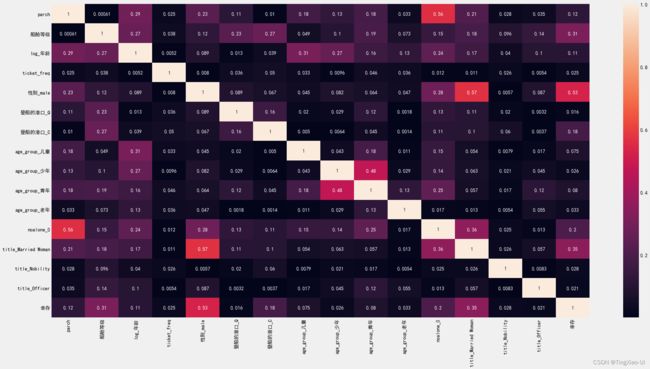
plt.figure(figsize=(30,15))
features_corr = features.corr().abs()
sea.heatmap(features_corr,annot=True)

数据集中高度共线变量可能是多余的，我们只需保留其中一个特征即可为模型提供必要的信息。

删除共线特征是一种通过减少特征数量来降低模型复杂性的方法，可以帮助增加模型泛化。

它还可以帮助我们解释模型，因为我们只需要考虑单个变量。

有许多方法可以消除共线特征，例如使用方差膨胀因子

我们将使用更简单的度量标准，

并删除相关系数高于某个阈值的特征

以下代码

通过删除所比较的两个特征之一，根据我们为相关系数选择的阈值来移除共线特征。
它还打印其删除的相关性，以便我们可以看到调整阈值的效果。

我们将使用0.6的阈值，如果特征之间的相关系数超过该值，则删除一对特征中的一个。

过滤冗余特征(共线特征)

def delCorrFeatrue(inx,iny,th):#删除相似特征:根据特征与特征的相关性大小以及特征与目标的相关性高低做判断是删除i还是j
    #特征与目标相关性
    data = pd.concat([inx,iny],axis=1)
    data_corr = data.corr().abs()[iny.columns[0]]
    #特征与特征相关性
    cols = inx.columns # 获取特征列的名称
    corr_list = []
    size = inx.shape[1]
    high_corr_fea = [] # 存储相关系数大于0.6的特征名称
    features_corr = inx.corr().abs()
    #筛选高于阈值的特征
    for i in range(0,size):
        for j in range(i+1, size):
            if(abs(features_corr.iloc[i,j])>= th):
                corr_list.append([features_corr.iloc[i,j], i, j]) # features_corr.iloc[i,j]：按位置选取数据

    sorted_corr_list = sorted(corr_list, key=lambda xx:-abs(xx[0]))
    #遍历列表
    for v,i,j in sorted_corr_list:#根据特征与目标的相关性高低做判断是删除i还是j
        if data_corr[cols[i]]>=data_corr[cols[j]]:
            high_corr_fea.append(cols[j])
        else:
            high_corr_fea.append(cols[i])
    #列表去重
    high_corr_fea = list(set(high_corr_fea))
    # 删除特征
    #inx.drop(labels=high_corr_fea,axis=1,inplace=True)
    inx = inx.drop(high_corr_fea,axis=1)
    return inx

# 删除大于指定相关系数的共线特征
features = delCorrFeatrue(features,targets, 0.6)

我们的最终数据集现在有15个特征。特征很多,主要是因为我们有一个one-hot编码的分类变量。此外，诸如随机森林之类的模型执行隐式特征选择并自动确定在训练期间哪些特征是重要的。

4.6.1.1其他特征选择方法

有更多的特征选择方法。一些流行的方法包括主成分分析（PCA），它将特征转换为保持最大方差的减少数量的维度，或独立成分分析（ICA），旨在找到一组特征中的独立源。

然而，虽然这些方法在减少特征数量方面是有效的，但它们创造了没有物理意义的新特征，因此几乎不可能解释模型。这些方法对于处理高维数据非常有用。

4.6.2 查看特征和目标之间的相关性

如果特征和目标之间是存在线性关系时才可以采用

即使某个特征和目标的线性无关，也不能说明该特征和目标之间无关，因为可能存在非线性关系。此外，与目标相关性低的特征对模型的作用也不一定小，与目标相关性低的特征的额外信息也可以提高性能。

组合数据

data_select = pd.concat([features,targets],axis=1)

plt.figure(figsize=(30,15))
data_corr = data_select.corr().abs()
sea.heatmap(data_corr,annot=True)

查看当前数据缺失值情况

missing_values_table(data_select)

确保所有值都是有限的

np.isfinite(data_select).sum().value_counts()

至此，特征工程阶段已完工，当前数据：无缺失值、重复值、冗余特征减少、均为有限值，此时可以将数据存入数据库或excel中。

4.6.3 保存数据

如果需要保存已经处理好的数据集可以用下面的代码：

x 保存为 training_features.csv
x_test保存为 testing_features.csv
y 保存为 training_labels.csv
y_test 保存为testing_labels.csv

#按照索引，拆分数据为训练集和测试集
# x_train = features.iloc[:x_train.shape[0],:]
# x_test = features.iloc[x_train.shape[0]:,:]
#训练集
x_train=data_select.iloc[:x_train.shape[0],:]
x_train=x_train.drop(columns='幸存')
y_train = targets.iloc[:x_train.shape[0],:]
#测试集
x_test=data_select.iloc[x_train.shape[0]:,:]
x_test=x_test.drop(columns='幸存')
y_test = targets.iloc[x_train.shape[0]:,:]
x_train.info()

#保存数据
x_train.to_csv(r'./Data/Titanic Dataset/train_features.csv',index=False)
y_train.to_csv(r'./Data/Titanic Dataset/train_laels.csv',index=False)
x_test.to_csv(r'./Data/Titanic Dataset/test_features.csv',index=False)
y_test.to_csv(r'./Data/Titanic Dataset/test_laels.csv',index=False)

4.6.4 小结

到目前为止，我们完成了

清理并格式化原始数据

进行探索性数据分析以了解数据集

开发了一系列我们将用于模型的特征

这三个步骤通常按此顺序执行，但我们可能会稍后再回来，根据我们的建模结果进行更多的EDA或特征工程。数据科学是一个迭代过程，我们一直在寻找改进以前工作的方法。

5 建模、预测和解决问题

5.1 需要评估的模型

现在我们已经准备好训练模型并预测所需的解决方案了。有60多种预测建模算法可供选择。我们必须了解问题的类型和解决方案的需求，将范围缩小到我们可以评估的少数几个模型。我们的问题是一个分类问题，我们想要确定输出(是否存活)与其他变量或特征(性别、年龄、港口等)之间的关系。当我们用给定的数据集训练我们的模型时，我们也在进行一类被称为监督学习的机器学习。有了这两个标准-监督学习加上分类，我们可以缩小我们的模型选择，包括:

逻辑回归
SVM 支持向量机
K近邻分类
朴素贝叶斯分类器
决策树
随机森林分类
梯度提升分类
感知机
人工神经网络

逻辑回归：逻辑回归是一个非常经典的算法，虽然被称为回归，但其实际上是一个分类模型，并常用于二分类。

优点：就是简单、可并行化、可解释强。

缺点：对于多重共线性很敏感，如果出现高相关的特征，需要使用因子分析、聚类分析等方法进行拆解降维。

SVM 支持向量机:已监督学习方式对数据进行二元分类的广义线性分类器,简单来说就是进行一个二分类,求解最优的那个分类面,然后用这个最优解进行分类

优点：鲁棒性强,对样本要求不高。

缺点：SVM的超参数需要通过交叉验证得到，非常耗费时间，而且SVM的核函数必须是正定的，计算量大,多分类很难使用。

K近邻：KNN是测量不同特征值之间的距离来进行分类，类似于近朱者赤近墨者黑，往往通过轮廓系数、交叉检验来找最优解

优点：简单易懂。

缺点：计算量大,对于不平衡样本处理起来较困难。

朴素贝叶斯分类器:贝叶斯模型非常特殊，是一个概率模型，通过事件属性相关事件发生的概率（先验概率）去推测该事件发生的概率。

优点：对缺失数据不太敏感，算法也比较简单，常用于文本分类、邮件分类等。

缺点：贝叶斯是一个理论上的模型，主要是因为贝叶斯首先是假设各特征之间是相互独立，通常很难保证，还有先验概率通常是假设出来，并不一定准确。

决策树:决策树（分类树）是一种十分常用的分类方法，使用信息熵增益、信息熵增益率、Gini系数等进行剪枝寻求最优解

优点：可解释性强、对样本要求较低。

缺点：容易过拟合，寻求最优解往往会形成一个NP难（能在多项式时间内验证得出一个正确解）问题。

随机森林:随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定

优点：鲁棒性好，既可以分类又可以回归，准确度高。

缺点：黑盒模型、计算量大。

梯度提升回归:

优点：
缺点：

感知机:找一个超平面来分类

优点：简单。

缺点：通常只能用来二分类问题，对于非线性问题效果差。

人工神经网络:人工神经网络就是模拟人思维的第二种方式。这是一个非线性动力学系统，其特色在于信息的分布式存储和并行协同处理。

优点：准。

缺点：黑盒模型、计算要求高，有时候可能比挖比特币更复杂，有时间跑神经网络我为什么不用来挖比特币呢。

为了比较模型，我们将主要使用Scikit-Learn默认的模型超参数值。通常这些将表现得很好，但应该在实际使用模型之前进行优化。

首先，我们只想确定每个模型在默认参数下的性能，

然后我们可以选择性能最佳的模型，调整超参数来进行进一步优化。

5.2 分类模型评估指标

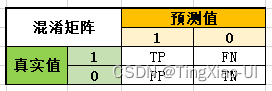
混淆矩阵：多个类别是否有混淆。混淆矩阵是ROC曲线绘制的基础，同时它也是衡量分类型模型准确度中最基本，最直观，计算最简单的方法。一句话解释就是：混淆矩阵就是分别统计分类模型归错类，归对类的观测值个数，然后把结果放在一个表里展示出来。这个表就是混淆矩阵。

ROC曲线：纵坐标：TPR，横坐标：FPR，此方法仅适用于于二元分类任务。

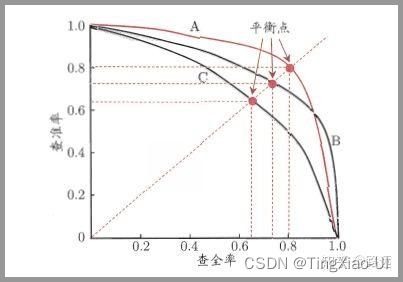
曲线与FP_rate轴围成的面积（记作AUC）越大，说明性能越好，即：曲线越靠近A点(左上方）性能越好，曲线越靠近B点（右下方）曲线性能越差。

A点是最完美的performance点，B处是性能最差点。

位于C-D线上的点说明算法性能和随机猜测是一样的–如C、D、E点。位于C-D之上说明算法性能优于随机猜测–如G点，位于C-D之下说明算法性能差于随机猜测–如F点。

ROC曲线在高不平衡数据条件下仍能够很好的展示实际情况

 可选度量：

TPR：真正率、召回率、灵敏度=预测为正实际为正(TP)/实际为正(TP+FN)

FPR：假真率==预测为正实际为负(FP)/实际为负(TN+FP)

准确率：分类正确的总个数/总样本数，在样本分布非常不均衡的情况下，准确率偏向于多数类样本而不能描述少数类样本的预测准确度

召回率(灵敏度)=预测为正实际为正(TP)/实际为正(TP+FN)，召回率越高，则模型对正样本被预测出来的概率越高，表示表示模型预测响应的覆盖程度

精确率/查准率预测为正实际为正(TP)/预测为正(TP+FP)，表示表示预测为正的样本中有多少是预测对的。精准率代表对正样本结果中的预测准确程度，而准确率则代表整体的预测准确程度，既包括正样本，也包括负样本。

F1_score:精确率（Precision）和召回率（Recall）之间的关系用图来表达，就是下面的PR曲线：可以发现他们俩的关系是「两难全」的关系。为了综合两者的表现，在两者之间找一个平衡点，就出现了一个> F1分数。F1_score=召回率与精确率的调和平均

如何判断 ROC 曲线的好坏？

FPR 表示模型虚报的响应程度，而 TPR 表示模型预测响应的覆盖程度。我们所希望的当然是：虚报的越少越好，覆盖的越多越好。所以总结一下就是TPR 越高，同时 FPR 越低（即 ROC 曲线越陡），那么模型的性能就越好。参考如下：

ROC 曲线无视样本不平衡

TPR和FPR分别是基于类别1和0出发的，也就是说它们分别在实际的正样本和负样本中来观察相关概率问题。正因为如此，选用这两个指标的ROC，无论样本是否平衡，都不会被影响，用动态图的形式展示一下它是如何工作的。可以发现：无论红蓝色样本比例如何改变，ROC 曲线都没有影响。

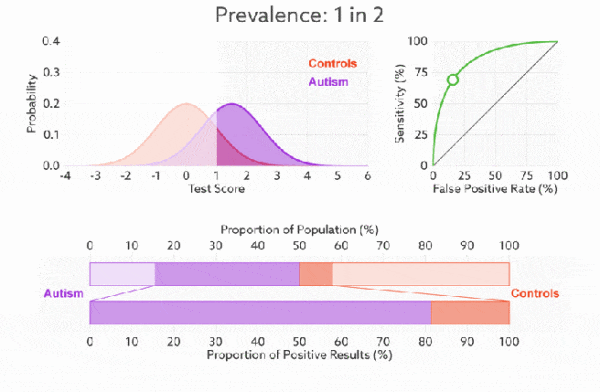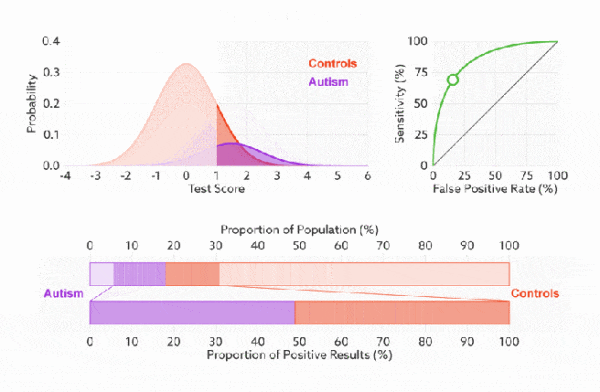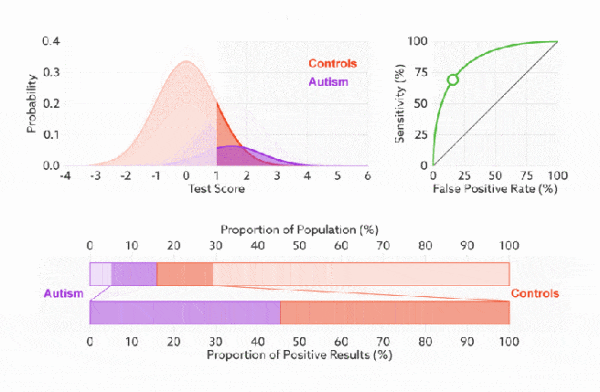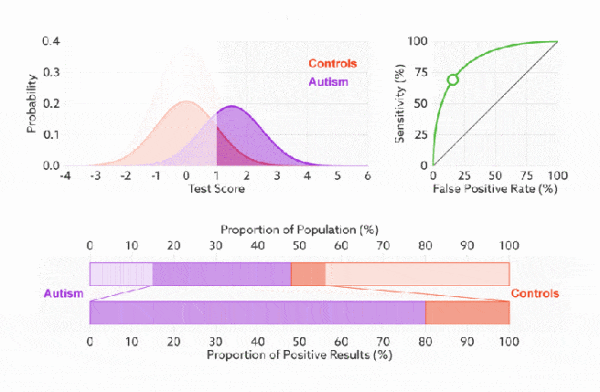
AUC(ROC曲线下面积)：AUC常常被用来评价模型的好坏
基尼系数=2AUC-1：若基尼系数高于60%，就是一个很好的模型
Lift（提升）和Gain（增益）增益和提升图主要哦难过与检查概率的等级排序
K-S图：用来衡量正负分布之间分离程度的指标

使用cross_val_score交叉验证评估模型

交叉验证用于评估模型的预测性能，尤其是训练好的模型在新数据上的表现，可以在一定程度上减小过拟合。

可以从有限的数据中获取尽可能多的有效信息。

# from sklearn.model_selection import cross_val_score
# cross_val_score(estimator, X, y=None, *, groups=None, scoring=None, cv=None, n_jobs=None, verbose=0, fit_params=None, pre_dispatch="2*n_jobs", error_score=np.nan)

cross_val_score参数定义：

estimator：估计器，也就是模型

X, y：数据，标签值

soring：调用的方法

cv：交叉验证生成器或可迭代的次数

n_jobs：同时工作的cpu个数（-1代表全部）

verbose：日志冗长度，int：冗长度，0：不输出训练过程，1：偶尔输出，>1：对每个子模型都输出

fit_params：传递给估计器的拟合方法的参数

pre_dispatch：控制并行执行期间调度的作业数量。减少这个数量对于避免在CPU发送更多作业时CPU内存消耗的扩大是有用的。

cv参数：

无，要使用默认的 5 倍交叉验证，

int，用于指定中折叠的次数，(Stratified)KFold，如果估计器是分类器并且是二元或多类，则使用分层KFold。在所有其他情况下使用
KFold。

CV分路器：如StratifiedKFold、KFold、

可迭代的收益率（训练、测试）拆分为索引数组。

pre_dispatch参数：

none，在这种情况下，所有的工作立即创建并产生。将其用于轻量级和快速运行的作业，以避免由于按需产生作业而导致延迟

一个int，给出所产生的总工作的确切数量

一个字符串，给出一个表达式作为n_jobs的函数，如’2 * n_jobs’

Scoring参数：

Scoring	Function	Comment
分类
‘accuracy’	metrics.accuracy_score	准确率：分类正确的总个数/总样本数
‘balanced_accuracy’	metrics.balanced_accuracy_score	均衡准确率，适用于类不平衡数据集。
‘average_precision’	average_precision
'precision’etc.	metrics.precision_score	精确率/查准率：TP/(TP+FP)
'recall’etc.	metrics.recall_score	召回率/灵敏度:TP/(TP+FN)
‘roc_auc’	metrics.roc_auc_score	曲线下方的蓝色区域的面积表示了模型的分类能力，面积越大分类能力越强
‘f1’	metrics.f1_score	召回率与精确率的调和平均
‘f1_micro’	metrics.f1_score
‘f1_macro’	metrics.f1_score
‘f1_weighted’	metrics.f1_score
‘f1_samples’	metrics.f1_score
‘neg_log_los’	metrics.log_loss
回归
‘explained_variance’	metrics.explained_variance_score	可解释方差
‘neg_mean_absolute_error’	metrics.mean_absolute_error	平均绝对值误差
‘neg_mean_squared_error’	metrics.mean_squared_error	均方根误差
‘neg_mean_squared_log_error’	metrics.mean_squared_log_error	均方对数误差
‘neg_median_absolute_error’	metrics.median_absolute_error	中位绝对误差
‘r2’	metrics.r2_score
聚类
‘adjusted_mutual_info_score’	metrics.adjusted_mutual_info_score
‘adjusted_rand_score’	metrics.adjusted_rand_score
‘completeness_score’	metrics.completeness_score
‘fowlkes_mallows_score’	metrics.fowlkes_mallows_score
‘homogeneity_score’	metrics.homogeneity_score
‘mutual_info_score’	metrics.mutual_info_score
‘normalized_mutual_info_score’	metrics.normalized_mutual_info_score
‘v_measure_score’	metrics
‘accuracy’	metrics.v_measure_score

导入库

# 机器学习模型
from sklearn.linear_model import LogisticRegression#逻辑回归
from sklearn.svm import SVC, LinearSVC#支持向量机
from sklearn.neighbors import KNeighborsClassifier#KNN
from sklearn.naive_bayes import GaussianNB#朴素贝叶斯
from sklearn.linear_model import Perceptron#感知机
from sklearn.neural_network import MLPClassifier#人工神经网络
from sklearn.tree import DecisionTreeClassifier#决策树
from sklearn.ensemble import GradientBoostingClassifier#梯度提升分类树
from sklearn.ensemble import RandomForestClassifier#随机森林

# 超参数调整
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
#分层交叉验证
from sklearn.model_selection import StratifiedKFold
#评估分类性能
from sklearn.metrics import accuracy_score  #for accuracy_score
from sklearn.model_selection import KFold #for K-fold cross validation
from sklearn.model_selection import cross_val_score #score evaluation
from sklearn.model_selection import cross_val_predict #prediction
from sklearn.metrics import confusion_matrix #混淆矩阵
from sklearn.metrics import roc_curve,auc#ROC，AUC
#绘制学习曲线、验证曲线
from sklearn.model_selection import learning_curve,validation_curve

读取格式化后的数据

train_features = pd.read_csv(r'./Data/Titanic Dataset/train_features.csv')
train_labels = pd.read_csv(r'./Data/Titanic Dataset/train_laels.csv')
test_features = pd.read_csv(r'./Data/Titanic Dataset/test_features.csv')
test_labels = pd.read_csv(r'./Data/Titanic Dataset/test_laels.csv')
# # Display sizes of data
print('Training Feature Size: ', train_features.shape)
print('Testing Feature Size:  ', test_features.shape)
print('Training Labels Size:  ', train_labels.shape)
print('Testing Labels Size:   ', test_labels.shape)

X_train= np.array(train_features)#m*n
X_test=np.array(test_features)#m*n
# Y_train = np.array(train_labels)#m*1
# Y_test=np.array(test_labels)#m*1
Y_train = np.array(train_labels).reshape((-1, ))#m
Y_test = np.array(test_labels).reshape((-1, ))#m

5.3 建立Baseline

在我们开始制作机器学习模型之前建立一个基线是很重要的。如果我们构建的模型不能胜过基线，那么我们可能不得不承认机器学习不适合这个问题。这可能是

没有使用正确的模型

需要更多的数据

或者因为有一个更简单的解决方案不需要机器学习。

建立基线至关重要，因此我们最终可能不会构建机器学习模型，只是意识到我们无法真正解决问题。

对于回归任务，一个好的基线是为测试集上的所有实例预测目标在训练集上的中值。这很容易实现，并为我们的模型设置了相对较低的标准：如果它们不能比猜测中值更好，那么我们需要重新考虑我们的方法。

对于分类任务，选取一种机器学习模型，使用默认超参数参数以及评分标准，使用分层交叉验证评估模型选取平均分。

#创建基线模型：随机森林，默认参数
base_model = RandomForestClassifier(random_state=123)  #基线模型base_line model
#分层交叉验证评估
baseline_score = cross_val_score(base_model, X_train, Y_train, cv=StratifiedKFold(n_splits=5))
#取平均得分
baseline_score = round(baseline_score.mean()*100,2)
print(baseline_score)

5.4 模型评估与选择

from sklearn.model_selection import cross_val_score
# cross_val_score(estimator, X, y=None, *, groups=None, scoring=None, cv=None, n_jobs=None, verbose=0, fit_params=None, pre_dispatch="2*n_jobs", error_score=np.nan)

# 逻辑回归
log = LogisticRegression(random_state=123)
log.fit(X_train,Y_train)
# Y_pre = log.predict(X_test)#测试集预测
acc_log_train = round(log.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_log_test = round(log.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_log_train,acc_log_test)

cross_val_score(log, X_train, y=Y_train, scoring=None, cv=5).mean()

#svc
svm = SVC(random_state=123)
svm.fit(X_train,Y_train)
# Y_pred = svm.predict(X_test)#测试集预测
acc_svm_train = round(svm.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_svm_test = round(svm.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_svm_train,acc_svm_test)
cross_val_score(svm, X_train, y=Y_train, scoring=None, cv=5).mean()

#LinearSVC
linear_svc = LinearSVC(random_state=123)
linear_svc.fit(X_train, Y_train)
# Y_pred = linear_svc.predict(X_test)#测试集预测
acc_linear_svc_train = round(linear_svc.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_linear_svc_test = round(linear_svc.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_linear_svc_train,acc_linear_svc_test)
cross_val_score(linear_svc, X_train, y=Y_train, scoring=None, cv=5).mean()

Knn = KNeighborsClassifier()
Knn.fit(X_train,Y_train)
# Y_pred = Knn.predict(X_test)#测试集预测
acc_Knn_train = round(Knn.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_Knn_test = round(Knn.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_Knn_train,acc_Knn_test)
cross_val_score(Knn, X_train, y=Y_train, scoring=None, cv=5).mean()

#朴素贝叶斯
bys = GaussianNB()
bys.fit(X_train, Y_train)
# Y_pred = bys.predict(X_test)#测试集预测
acc_gaussian_train = round(bys.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_gaussian_test = round(bys.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_gaussian_train,acc_gaussian_test)
cross_val_score(bys, X_train, y=Y_train, scoring=None, cv=5).mean()

#决策树
decision_tree = DecisionTreeClassifier(random_state=123)
decision_tree.fit(X_train, Y_train)
# Y_pred = decision_tree.predict(X_test)#测试集预测
acc_decision_tree_train = round(decision_tree.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_decision_tree_test = round(decision_tree.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_decision_tree_train,acc_decision_tree_test)
cross_val_score(decision_tree, X_train, y=Y_train, scoring=None, cv=5).mean()

plt.figure(figsize=(14,6))
tree.plot_tree(decision_tree) #打印决策树的结构图
plt.show()

#随机森林
random_forest = RandomForestClassifier(random_state=123)#n_estimators:默认100
random_forest.fit(X_train, Y_train)
# Y_pred = random_forest.predict(X_test)#测试集预测
acc_random_forest_train = round(random_forest.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_random_forest_test = round(random_forest.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_random_forest_train,acc_random_forest_test)
cross_val_score(random_forest, X_train, y=Y_train, scoring=None, cv=5).mean()

#梯度提升分类树
GB_forest = GradientBoostingClassifier(random_state=123)#n_estimators:默认100
GB_forest.fit(X_train, Y_train)
# Y_pred = GB_forest.predict(X_test)#测试集预测
acc_GB_forest_train = round(GB_forest.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_GB_forest_test = round(GB_forest.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_GB_forest_train,acc_GB_forest_test)
cross_val_score(GB_forest, X_train, y=Y_train, scoring=None, cv=5).mean()

#感知机
perceptron = Perceptron(random_state=123)
perceptron.fit(X_train, Y_train)
# Y_pred = perceptron.predict(X_test)#测试集预测
acc_perceptron_train = round(perceptron.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_perceptron_test = round(perceptron.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_perceptron_train,acc_perceptron_test)
cross_val_score(perceptron, X_train, y=Y_train, scoring=None, cv=5).mean()

#人工神经网络
ann = MLPClassifier(random_state=123)
ann.fit(X_train, Y_train)
# Y_pred = ann.predict(X_test)#测试集预测
acc_ann_train = round(ann.score(X_train, Y_train) * 100, 2)#训练集上的评分
acc_ann_test = round(ann.score(X_test, Y_test) * 100, 2)#测试集上的评分
print(acc_ann_train,acc_ann_test)
cross_val_score(ann, X_train, y=Y_train, scoring=None, cv=5).mean()

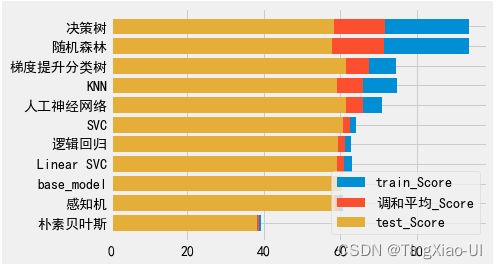
查看模型综合得分(调和平均)

models = pd.DataFrame({
    'Model': ['SVC', 'KNN', '逻辑回归', 
              '随机森林', '朴素贝叶斯', '感知机', 
              '人工神经网络', 'Linear SVC', 
              '决策树','梯度提升分类树','base_model'],
        'train_Score': [acc_svm_train, acc_Knn_train, acc_log_train,
              acc_random_forest_train, acc_gaussian_train,acc_perceptron_train,
              acc_ann_train,acc_linear_svc_train, acc_decision_tree_train,acc_GB_forest_train,
                 baseline_score],
         'test_Score': [acc_svm_test, acc_Knn_test, acc_log_test, 
              acc_random_forest_test, acc_gaussian_test, acc_perceptron_test, 
              acc_ann_test, acc_linear_svc_test, acc_decision_tree_test,acc_GB_forest_test,
                 baseline_score]})
models['调和平均']=pd.DataFrame(2/(1/models['train_Score']+1/models['test_Score']))
# models.sort_values(by='调和平均', ascending=True).plot(x = 'Model',y = '调和平均',kind = 'barh',color = 'red', edgecolor = 'black')

index=models.sort_values(by='调和平均', ascending=True).index
data_plot=models.loc[index,:]
plt.barh(data_plot.Model,data_plot.train_Score) # 对每个特征绘制总数状图
plt.barh(data_plot.Model,data_plot.调和平均,alpha=1)
plt.barh(data_plot.Model,data_plot.test_Score,alpha=1) 

plt.legend(['train_Score','调和平均_Score','test_Score'])

当前的机器模型中除了朴素贝叶斯、感知机模型外均优于基线

综合训练集和测试集得分，决策树表现最好其次是随机森林，但是随机森林更优，因为随机森林可以降低决策树过拟合的程度

当前模型使用默认的超参数情况下做了初步评估，需要进一步调整超参数以客观评估模型

从这里开始，我们将专注于使用超参数调优来优化最佳模型。鉴于此处的结果，我们将专注于使用随机森林。

5.5 模型调整超参数

在机器学习中，优化模型意味着为特定问题找到最佳的超参数集。

5.5.1超参数

模型超参数、参数定义：

模型超参数被认为最好通过机器学习算法来进行设置，在训练之前由数据科学家调整。例如，随机森林中的树木数量，或者K-Nearest Neighbors Regression中使用的邻居数量k，聚类算法中簇的数量。

模型参数是模型在训练期间学习的内容，例如线性回归中的权重。

我们作为数据科学家通过选择超参数来控制模型，这些选择会对模型的最终性能产生显着影响（尽管通常不会像获取更多数据或工程特征那样有效）。调整模型超参数可以控制模型中欠拟合与过拟合的平衡。

欠拟合：我们可以尝试通过制作更复杂的模型来校正欠拟合，例如在随机森林中使用更多树或在深度神经网络中使用更多层。当我们的模型没有足够的容量（自由度）来学习特征和目标之间的关系时，模型会发生欠拟合并且具有高偏差。

过拟合：我们可以通过限制模型的复杂度和应用正则化来尝试纠正过度拟合。这可能意味着降低多项式回归的次数，或将衰退层添加到深度神经网络。 过拟合的模型具有高方差并且实际上记住了训练集。

5.5.2 常见设置超参数的做法有

猜测和检查：根据经验或直觉，选择参数，一直迭代。

网格搜索：让计算机尝试在一定范围内均匀分布的一组值。

随机搜索：让计算机随机挑选一组值。

贝叶斯优化：使用贝叶斯优化超参数，会遇到贝叶斯优化算法本身就需要很多的参数的困难。

在良好初始猜测的前提下进行局部优化：这就是 MITIE 的方法，它使用 BOBYQA 算法，并有一个精心选择的起始点。由于 BOBYQA 只寻找最近的局部最优解，所以这个方法是否成功很大程度上取决于是否有一个好的起点。在 MITIE
的情下,我们知道一个好的起点，但这不是一个普遍的解决方案，因为通常你不会知道好的起点在哪里。从好的方面来说，这种方法非常适合寻找局部最优解。稍后我会再讨论这一点。

最新提出的 LIPO 的全局优化方法。这个方法没有参数，而且经验证比随机搜索方法好。

下面使用随机搜索和交叉验证进行超参数调整来缩小最佳超参数范围，然后使用网络搜索进一步精确超参数范围

5.6 使用随机搜索和交叉验证进行超参数调整

随机搜索：

定义一系列选项，然后随机选择要尝试的组合(网络搜索是尝试所有组合)

通常，对模型最佳超参数的知识有限时，使用随机搜索更好，我们可以使用随机搜缩小选项范围，然后使用更有限的选项范围进行网络搜索。

交叉验证是用于评估超参数性能的方法：针对分类模型，我们使用分层k-fold交叉验证，而不是将训练设置拆分为单独的训练和验证集(减少了可以使用的训练数据量)。
将原始数据分为N份，每次让模型在N-1份数据上训练，剩下1份上验证。最后把N次验证的分数取平均，来尽可能客观地评价模型算法的性能，从而达到所谓的“尽可能充分利用数据”的目的。

这意味着将训练数据划分为K个折叠，然后进行迭代过程，我们首先在K-1个折叠上进行训练，然后评估第K个折叠的性能。
我们重复这个过程K次，所以最终我们将测试训练数据中的每个例子，关键是每次迭代我们都在测试我们之前没有训练过的数据。

在分层K-Fold交叉验证结束时，我们将每个K次迭代的平均误差/得分作为最终性能度量，然后立即在所有训练数据上训练模型。

我们记录的性能用于比较超参数的不同组合。

5折交叉验证示意图

优点：

适合小样本的数据集

经过多次划分，大大降低了结果的偶然性，从而提高了模型的准确性。

对数据的使用效率更高。train_test_split，默认训练集、测试集比例为3:1。如果是5折交叉验证，训练集比测试集为4:1；10折交叉验证训练集比测试集为9:1。数据量越大，模型准确率越高。

缺点：

对数据随机均等划分，不适合包含不同类别的数据集。比如：数据集有5类数据（ABCDE各占20%），抽取出来的也正好是按照类别划分的5类，第一折全是A，第二折全是B……这样就会导致，模型学习到测试集中数据的特点，用BCDE训练的模型去测试A类数据、ACDE的模型测试B类数据，这样准确率就会很低。

所以对于分类问题，应使用分层交叉验证以避免随机划分后的结果中正负样本比例不一致，导致模型准确率下降。

分层5折交叉验证示意图

在这里，我们将使用分层交叉验证实现随机搜索，以选择随机森林的最佳超参数。我们首先定义一个网格，然后执行以下迭代过程：

从网格中随机抽样一组超参数，使用分层5倍交叉验证评估超参数，

然后选择具有最佳性能的超参数。

通过随机搜索减小各个超参数的搜索范围，然后以随机搜索的超参数结果为基础，使用网络搜索进一步缩小超参数范围来确定最佳超参数

5.6.1 使用随机搜索缩小超参数范围

随机森林超参数选项

我们选择了4个不同的超参数来调整随机森林。这些都将以不同的方式影响模型，这些方法很难提前确定，找到特定问题的最佳组合的唯一方法是测试它们！

# 随机森林使用的树的数量(估算器数量)
n_estimators = [2,5,10,20,50,80,100,150,200,300,400,500,600]
#  树的最大深度
max_depth = [2,3,5,10,15]
# 每片叶子的最小样本数
min_samples_leaf = [1,2,4,6,8]
# 拆分节点的最小样本数
min_samples_split = [2,4,6,10,16,20]
# 进行拆分时要考虑的最大特征数
max_features = ['auto', 'sqrt', 'log2', None]
# 定义要进行搜索的超参数网格
hyperparameter = {'n_estimators': n_estimators,
                       'max_depth': max_depth,
                       'min_samples_leaf': min_samples_leaf,
                       'min_samples_split': min_samples_split,
                 'max_features': max_features}

在下面的代码中，我们创建了随机搜索对象，传递以下参数：

estimator: 估计器，也就是模型

param_distributions: 我们定义的参数

cv ：用于k-fold交叉验证的folds 数量，若是cv=k，表示k-fold；若是cv=StratifiedKFold(n_splits=k),表示分层k-fold交叉验证

n_iter: 不同的参数组合的数量

scoring: 评估指标

n_jobs: 同时工作的cpu个数（-1代表全部）

verbose: 日志冗长度，int：冗长度，0：不输出训练过程，1：偶尔输出，>1：对每个子模型都输出

return_train_score: 每一个cross-validation fold 返回的分数

random_state: 修复使用的随机数生成器，因此每次运行都会得到相同的结果

随机搜索对象的训练方式与任何其他scikit-learn模型相同。训练之后，我们可以比较所有不同的超参数组合，找到效果最好的组合。

#创建用于调整超参数的模型：随机森林
model = RandomForestClassifier(random_state=123)#random_state:随机数种子，程序每运行一次，都会得到不同的准确率，无法调参。这个时候就是因为没有加random_state。加上以后就可以调参了

#使用分层5折交叉验证设置随机搜索
random_cv=RandomizedSearchCV(estimator=model,
                            param_distributions=hyperparameter,
                            cv=StratifiedKFold(n_splits=10),
                            n_iter=200,
                            scoring=None,
                            n_jobs=-1,
                            verbose = 1,
                            return_train_score = True,
                            random_state=123)

# 拟合随机搜索
random_cv.fit(X_train,Y_train)

使用分层交叉验证随机搜索获得的最佳模型参数

random_cv.best_estimator_

5.6.2 使用网络搜索精确超参数范围

使用随机搜索是缩小可能的超参数以尝试的好方法。最初，我们不知道哪种组合效果最好，但这至少缩小了选项的范围。我们可以通过使用随机搜索结果来创建具有超参数的网格来进行网格搜索，这些参数接近于在随机搜索期间最佳的参数。

但是，我们不会再次评估所有这些设置，而是将重点放在单个树林中的树的数量（n_estimators）上。通过仅改变一个超参数，我们可以直接观察它如何影响性能。我们预计会看到树木数量对欠拟合和过拟合的影响。在这里，

我们将使用仅具有n_estimators超参数的网格进行网格搜索(也可以选择别的参数)。

我们将评估一系列的树，然后绘制训练和测试性能，以了解增加树的数量对模型的影响。

我们将其他超参数固定为从随机搜索返回的最佳值，以隔离树的数量影响。

# 创建一系列要评估的树
trees_grid = {'n_estimators': list(range(240,260,1))}
# 使用随机搜索得到的最佳参数创建模型：
model = RandomForestClassifier(max_depth = 5,
                               max_features=None,
                               min_samples_leaf = 6,
                               min_samples_split=4,
                               random_state=123)
# 使用树的范围和随机森林模型的网格搜索对象
grid_search = GridSearchCV(estimator = model,
                          param_grid=trees_grid,
                          cv=StratifiedKFold(n_splits=10),
                           scoring = None,
                           verbose = 1,
                           n_jobs = -1, 
                           return_train_score = True) 

# 这里scoring评估模型参数使用平衡的准确率以评估泛化误差
# scoring = 'balanced_accuracy'计算平衡的准确性，从而避免对不平衡的数据集进行夸大的性能估计。
#它是每个班级的召回分数的宏观平均值，或者等效地，原始准确性，其中每个样本根据其真实类别的逆流行率进行加权。
#因此，对于平衡数据集，分数等于准确性。

#拟合网格搜索
grid_search.fit(X_train,Y_train)

使用分层交叉验证网络搜索获得的最佳模型参数

grid_search.best_estimator_

最佳随机森林模型具有以下超参数：

n_estimators = 245

max_depth = 5

min_samples_leaf = 6

min_samples_split = 4

max_features=None

# 将结果导入数据框
results = pd.DataFrame(grid_search.cv_results_)
# 绘制训练误差和测试误差与树木数量的关系图
plt.figure(figsize=(8, 8))
plt.style.use('fivethirtyeight')
plt.plot(results['param_n_estimators'],1-results['mean_train_score'], label = 'Training Error')
plt.plot(results['param_n_estimators'],1-results['mean_test_score'], label = 'Testing Error')
plt.xlabel('Number of Trees')
plt.ylabel('Error'); plt.legend()
plt.title('Performance vs Number of Trees')

5.7 绘制学习曲线和验证曲线

学习曲线学习曲线：模型性能 = f(训练集大小)，通过学习曲线观察学习的效果。

学习曲线是横轴为训练集大小，由此来看不同训练集大小设置下的模型准确率。学习曲线可以帮助我们理解训练数据集的大小对机器学习模型的影响。当遇到计算能力限制时，这一点非常有用。下面改变训练数据集的大小，把学习曲线画出来

验证曲线: 模型性能(得分) = f(超参数)

验证曲线是横轴为某个超参数的一系列值，由此来看不同参数设置下模型准确率。从验证曲线上可以看到随着超参数设置的改变，模型可能从欠拟合到合适再到过拟合的过程，进而选择一个合适的位置，来提高模型的性能。

在进行模型调参时：其他参数不变，绘制一个参数变化的训练曲线和验证曲线，选择训练效果和验证效果最佳时的参数。依次对每个参数进行绘制图形，调整得到相对优化的模型。

from sklearn.model_selection import validation_curve,learning_curve

# 使用随机搜索+网络搜索得到的最佳参数创建模型：
model = RandomForestClassifier(n_estimators=245,
                               max_depth = 5,
                               min_samples_leaf = 6,
                               max_features=None,
                               min_samples_split = 4,
                               random_state=123)

#生成学习曲线
size_grid = np.array([0.2,0.4,0.6,0.8,1])
_,train_scores,validation_scores  = learning_curve(model,X_train,Y_train,
                                                  train_sizes = size_grid, 
                                                  scoring='balanced_accuracy',
                                                  cv =StratifiedKFold(n_splits=5))

#学习曲线可视化
plt.figure()
l=features.shape[0]
plt.plot(size_grid*l,1-np.average(train_scores, axis = 1),label="Training score", color = 'red')
plt.plot(size_grid*l, 1-np.average(validation_scores ,axis = 1),label="validation score",color = 'black')
plt.title('学习曲线')
plt.xlabel('训练集样本大小')
plt.ylabel('误差')
plt.legend()
plt.show()

#生成验证曲线
# 创建一系列要评估的树
# trees_grid = {'n_estimators': list(range(10,200,10))}
params_grid= list(range(200,300,10))

#使用
train_scores,validation_scores = validation_curve(model,X_train,Y_train,
                                            param_name='n_estimators',param_range=params_grid,
                                            scoring='balanced_accuracy',
                                            cv=5)

train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
validation_scores_mean = np.mean(validation_scores, axis=1)
validation_scores_std = np.std(validation_scores, axis=1)


#可视化生成训练、验证曲线
plt.figure()
# plt.plot(params_grid, train_scores_mean,color = 'red')
# plt.plot(params_grid,test_scores_mean,color = 'black')

plt.plot(params_grid, 1-train_scores_mean, label='Training score',color='r')
plt.plot(params_grid, 1-validation_scores_mean, label='validation score',color='k')

plt.title('验证曲线')
plt.xlabel('number of estimator')
plt.ylabel('Error')
plt.legend()
plt.show()
#同样的方法可以验证其他变量对训练的影响，多次操作，进行参数调整

6 在测试集上评估最佳模型

我们将使用超参数调整中的最佳模型来对测试集进行预测。请记住，我们的模型之前从未见过测试集，所以这个性能应该是模型在现实世界中部署时的表现的一个很好的指标。

为了比较，我们还可以查看默认模型的性能。下面的代码创建最终模型，训练它（会有计时），并评估测试集。

# 默认模型
default_model = RandomForestClassifier(random_state=123)

# 选择最佳模型参数
final_model = grid_search.best_estimator_
final_model

%%timeit -n 1 -r 5
default_model.fit(X_train, Y_train)

%%timeit -n 1 -r 5
final_model.fit(X_train, Y_train)

default_model.fit(X_train, Y_train)#随机森林默认超参数
Y_pred_default = default_model.predict(X_test)#测试集预测值
# acc_default = round(default_model.score(X_test, Y_test) * 100, 2)#测试集上评分
cross_val_score(default_model, X_test, y=Y_pred_default, scoring='f1', cv=5).mean()

final_model.fit(X_train, Y_train)#随机森林优化超参数
Y_pred_final = default_model.predict(X_test)#测试集预测值
# acc_final = round(final_model.score(X_test, Y_test) * 100, 2)#测试集上评分
cross_val_score(final_model, X_test, y=Y_pred_final, scoring='f1', cv=5).mean()

round((acc_final-acc_default)/acc_default*100,2)

最终的模型比基线模型的性能提高了大约11％。机器学习通常是一个需要权衡的领域：

偏差与方差
准确性与可解释性
准确性与运行时间
以及使用哪种模型

6.1 输出模型评估报告(测试集)

# 模型评估 （测试集）
from sklearn.metrics import classification_report

final_model.fit(X_train, Y_train)
Y_test_pred = final_model.predict(X_test)     # y_test_pred是预测的结果
print(classification_report(Y_test,Y_test_pred))  # 评估模型（真实的值与预测的结果对比）

support：真实值每个类别出现的次数

precision：精确率：预测对个数/预测值这个类别的总个数

recall：召回率/灵敏度：预测对的个数/真实值的这个类别的总个数

F1_score: 精确度和召回率的调和平均值

精确度和召回率都高时， F1值也会高

F1值在1时达到最佳值（完美的精确度和召回率），最差为0

在二元分类中， F1值是测试准确度的量度

从模型的评估中我们可以得到精确率（precision）、召回率（recall）、F1-score，且该模型预测的准确率为63%。

计算基尼系数

from sklearn.metrics import auc
from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(Y_test,Y_test_pred,pos_label=1)#pos_label：用于设置正类的标签值
test_auc = auc(fpr,tpr)
test_gini=2*test_auc-1

6.2 小结

在4，5，6 步我们做了一下几件事：

特征缩放
评估和比较几种机器学习方法
超参数使用随机搜索和交叉验证来调整机器学习模型
评估测试集上的最佳模型

结果表明:

机器学习适用于我们的问题，最终模型能够将乘客生还的预测误差控制在43.51%以内。
我们还看到，超参数调整能够改善模型的性能。这是一个很好的提示，正确的特征工程和收集更多数据（如果可能！）比微调模型有更大的回报。
运行时间与精度之间的权衡，这是我们在设计机器学习模型时必须考虑的众多因素之一。

我们知道我们的模型是准确的，但我们知道为什么它能做出预测？机器学习过程的下一步至关重要：尝试理解模型如何进行预测。实现高精度是很好的，但如果我们能够找出模型能够准确预测的原因，那么我们也可以使用这些信息来更好地理解问题。例如，

模型依靠哪些特征来推断预测生还与否？
可以使用此模型进行特征选择，并实现更易于解释的更简单模型吗？

下面，我们将尝试回答这些问题并从项目中得出最终结论！

7. 解释模型结果

机器学习经常是一个黑盒子 criticized as being a black-box:我们把数据在这边放进去，它在另一边给了我们答案。虽然这些答案通常都非常准确，但该模型并未告诉我们它实际上如何做出预测。这在某种程度上是正确的，但我们可以通过多种方式尝试并发现模型如何“思考”，例如 Locally Interpretable Model-agnostic Explainer (LIME). 这种方法试图通过学习围绕预测的线性回归来解释模型预测，这是一个易于解释的模型！

我们将探索几种解释模型的方法：

特征重要性
模型解释器 (LIME)

导入一些我们需要的包

# 机器学习模型
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor

from sklearn import tree

# LIME用于解释预测
import lime 
import lime.lime_tabular

7.1 特征重要性

我们可以解释决策树集合的基本方法之一是通过所谓的特征重要性。这些可以解释为最能预测目标的变量。虽然特征重要性的实际细节非常复杂. (here is a Stack Overflow question on the subject,但是我们可以使用相对值来比较特征并确定哪些与我们的问题最相关。

在scikit-learn中，从训练好的树中提取特征重要性非常容易。我们将特征重要性存储在数据框中以分析和可视化它们。

# 将特征重要性提取到数据结构中
feature_results = pd.DataFrame({'feature': list(train_features.columns), 
                                'importance': final_model.feature_importances_})

# 显示最重要的前十名
feature_results = feature_results.sort_values('importance', ascending = False).reset_index(drop=True)

feature_results.head(10)

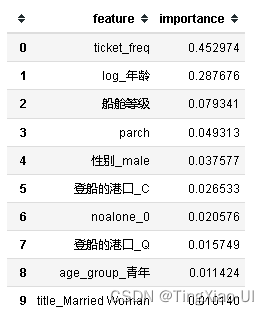
ticket_freq是最重要的特征(基于熵判别特征重要性)，这之后，特征的相对重要性大幅下降，这表明我们可能不需要保留所有特征来创建具有几乎相同性能的模型。

7.2 使用特征重要性进行特征选择

鉴于并非每个特征对于找到分数都很重要，如果我们使用更简单的模型（如线性回归）和随机森林中最重要特征的子集，会发生什么？线性回归确实优于基线，但与复杂模型相比表现不佳。

让我们尝试在逻辑回归中仅使用4个最重要的特征来查看性能是否得到改善。我们还可以限制这些特征并重新评估随机森林。

# 提取最重要特征的名称
most_important_features = feature_results['feature'][:3]

# 找到与每个特征名称对应的索引
indices = [list(train_features.columns).index(x) for x in most_important_features]

# 数据集中只保留最重要的特征
X_reduced = X_train[:,indices]
X_test_reduced = X_test[:,indices]

print('Most important training features shape: ', X_reduced.shape)
print('Most important testing  features shape: ', X_test_reduced.shape)

# 逻辑回归
log = LogisticRegression(random_state=123)
#在全部特征上拟合并测试
log.fit(X_train, Y_train)
print('全部特征')
print('测试集得分：',round(log.score(X_test, Y_test) * 100, 2))
print('训练集得分：',round(log.score(X_train, Y_train) * 100, 2))

# 在4个最重要的特征上拟合并测试（即减少后的特征上）
log.fit(X_reduced, Y_train)
print('减少特征')
print('测试集得分：',round(log.score(X_test_reduced, Y_test) * 100, 2))
print('训练集得分：',round(log.score(X_reduced, Y_train) * 100, 2))

可以看出，减少特征并没有显著改善逻辑回归的结果事实证明，低重要性特征中的额外信息确实可以提高性能。让我们看看在随机森林中使用减少的特征集。性能如何受到影响？

#随机森林
#在全部特征上拟合并测试
final_model.fit(X_train, Y_train)
print('全部特征')
print('测试集得分：',round(final_model.score(X_test, Y_test) * 100, 2))
print('训练集得分：',round(final_model.score(X_train, Y_train) * 100, 2))

# 在4个最重要的特征上拟合并测试（即减少后的特征上）
final_model.fit(X_reduced, Y_train)
final_model_reduced_pred = final_model.predict(X_test_reduced)
print('减少特征')
print('测试集得分：',round(final_model.score(X_test_reduced, Y_test) * 100, 2))
print('训练集得分：',round(final_model.score(X_reduced, Y_train) * 100, 2))

随着特征数量的减少，模型结果没有改变，我们将保留最终模型的所有特征。减少特征数量的初衷是因为我们总是希望构建最简约的模型：

即具有足够特征的最简单模型
使用较少特征的模型将更快地训练并且通常更容易解释。

在现在这种情况下，保留所有特征并不是主要问题，因为训练时间并不重要，我们仍然可以使用许多特征进行解释。

7.3 模型解释器

我们将使用LIME9(LIME to explain individual predictions )来解释模型所做的个别预测。 LIME是一项相对较新的工作，旨在通过用线性模型近似预测周围的区域来展示机器学习模型的思考方式。

我们将试图解释模型在两个例子上得到的预测结果：

其中一个例子得到的预测结果非常差
另一个例子得到的预测结果非常好。

我们将仅仅使用减少后的4个特征来帮助解释。虽然在4个最重要的特征上训练的模型稍微不准确，但我们通常必须为了可解释性的准确性进行权衡！

# 找到残差
residuals = abs(final_model_reduced_pred - Y_test)
    
# 提取最差和最好的预测的数据集
wrong = X_test_reduced[np.argmax(residuals), :]
right = X_test_reduced[np.argmin(residuals), :]

# 创造一个解释器对象
explainer = lime.lime_tabular.LimeTabularExplainer(
    training_data=X_reduced,
    feature_names=list(most_important_features),
    class_names=['bad', 'good'],
    mode='classification'
)

对最差预测的解释：

# 显示最差实例的预测值和真实值
print('Prediction: %0.4f' % final_model.predict(wrong.reshape(1, -1)))
print('Actual Value: %0.4f' % Y_test[np.argmax(residuals)])

# 最差预测的解释
wrong_exp = explainer.explain_instance(data_row = wrong, predict_fn =final_model.predict_proba)
# wrong_exp.show_in_notebook(show_table=True)

# # 画出预测解释
wrong_exp.as_pyplot_figure()
plt.title('Explanation of Prediction', size = 28)
plt.xlabel('Effect on Prediction', size = 22)

对最好预测的解释：

# 显示最好实例的预测值和真实值
print('Prediction: %0.4f' % final_model.predict(right.reshape(1, -1)))
print('Actual Value: %0.4f' % Y_test[np.argmin(residuals)])


# 最好预测的解释
right_exp = explainer.explain_instance(data_row = right, predict_fn =final_model.predict_proba)
# 画出预测解释
right_exp.as_pyplot_figure()
plt.title('Explanation of Prediction', size = 28)
plt.xlabel('Effect on Prediction', size = 22)

8 得出结论&&记录发现

8.1 得出结论

机器学习最后部分最重要的是：我们需要将我们学到的所有内容压缩成一个简短的摘要，仅突出最重要的发现。

就此项目而言，我们很简洁地总结了我们的工作。但是，在我们呈现和相应地定制信息时，了解我们的受众非常重要。这是一个用来申请工作的“作业”，考虑到这一点，这是我们需要在30秒内介绍的项目内容：

使用泰坦尼克号乘客生还数据，可以建立一个模型，可以乘客是否生还，误差在xx以内。
性别 and 船舱等级 是预测是否生还的最相关特征。

如果有人要求提供详细信息，那么我们可以轻松地解释所有实施步骤，并展示我们（希望）有充分记录的工作。机器学习项目的另一个重要方面是：

你已经注解了所有代码并使其易于跟进！
你希望别人（或者你自己在几个月内）能够看到你的工作并完全理解你做出的决定。

理想情况下，你应该编写代码，以便再次使用它。即使我们自己做项目，也可以练习正确的文档，当你想重新审视项目时，它会让你的生活更轻松。

8.2 记录发现

技术项目经常被忽视的部分是文档和报告。我们可以在世界上做最好的分析，但如果我们没有清楚地传达我们发现的结果，那么它们就不会产生任何影响！当我们记录数据科学项目时，我们会采用所有版本的数据和代码并对其进行打包，以便我们的项目可以被其他数据科学家复制或构建。重要的是要记住：

阅读代码的频率高于编写代码
如果我们几个月后再回来的话，我们希望确保我们的工作对于其他人和我们自己都是可以理解的,这意味着在代码中添加有用的注释并解释我们的推理。