机器学习----感知机(神经网络的基础)
什么是感知机?
机器学习中有分类和回归两大问题:
- 回归预测线性问题,例如房子价格、每一年的降水量 。
- 分类给物体分类,输出之后输出判断是一个香蕉还是一个苹果。
感知机是神经网络的基础
引入问题
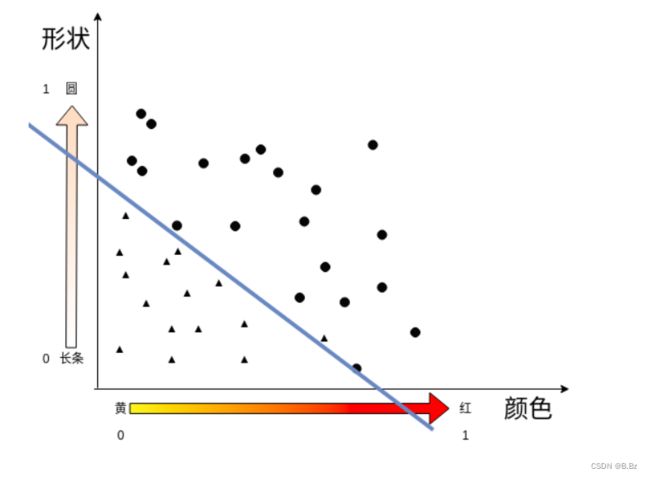
颜色越红,形状越圆的是苹果
颜色越黄,形状为长条的是香蕉
这是数据分布的散点图,怎么才能找到一个线来把香蕉和苹果分类出来呢?
决策边界
- y=mx + b是线性回归预测的数据都是分布在线上的点
- 分类问题产生一个决策线,在决策线上方的是一种输出(苹果),在决策线下方的又是一种输出(香蕉)。
决策边界线公式: m 1 x 1 + m 2 x 2 + b = 0 m_1x_1 + m_2x_2 + b = 0 m1x1+m2x2+b=0
-
这一条线就是决策边界,把坐标点带入到决策边界线中我们可以得到一个结果: s c o r e = m 1 x 1 + m 2 x 2 + b score = m_1x_1 + m_2x_2 + b score=m1x1+m2x2+b
-
如果计算出的结果大于0就说明在决策边界的上方,反之为下方:
f ( x ) = { s c o r e > 0 : A p p l e s c o r e < 0 : b a n a n a f(x) =\begin{cases}score >0:Apple\\ score <0:banana\end{cases} f(x)={score>0:Applescore<0:banana -
换成矩阵运算的方式: w e i g h t = [ w 1 w 2 b ] weight = \begin{bmatrix} w_1\\ w_2 \\ b \end{bmatrix} weight=⎣⎡w1w2b⎦⎤
f e a t u r e = [ x 1 x 2 1 ] feature = \begin{bmatrix} x_1 & x_2 & 1 \end{bmatrix} feature=[x1x21]
F e a t u r e ∗ W e i g h t > 0 = > A p p l e F e a t u r e ∗ W e i g h t < 0 = > B a n a n a Feature * Weight > 0 => Apple \\ Feature * Weight < 0 => Banana Feature∗Weight>0=>AppleFeature∗Weight<0=>Banana
f ( x 1 , x 2 ) ‾ = { 1 ( F e a t u r e W e i g h t > 0 ) 0 ( F e a t u r e W e i g h t < 0 ) \overline {f(x_1,x_2)}=\begin{cases}1\left( FeatureWeight >0\right) \\ 0\left( FeatureWeight <0\right) \end{cases} f(x1,x2)={1(FeatureWeight>0)0(FeatureWeight<0)
- 三维空间中的决策边界的计算:
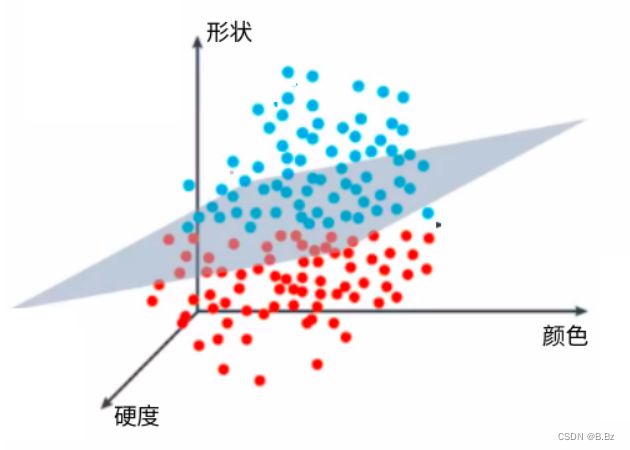
w e i g h t = [ w 1 w 2 w 3 b ] weight = \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ b \end{bmatrix} weight=⎣⎢⎢⎡w1w2w3b⎦⎥⎥⎤
f ( x 1 , x 2 , x 3 ) ‾ = { 1 ( F e a t u r e W e i g h t > 0 ) 0 ( F e a t u r e W e i g h t < 0 ) \overline {f(x_1,x_2,x_3)}=\begin{cases}1\left( FeatureWeight >0\right) \\ 0\left( FeatureWeight <0\right) \end{cases} f(x1,x2,x3)={1(FeatureWeight>0)0(FeatureWeight<0)
1. 激活函数
- 在计算是在决策边界的上方还是下方时,输出不可能完全是1或者0,有可能是正无穷或负无穷。
- 我们只需要输出1(苹果)或者0(香蕉)就可以了,
激活函数的作用就是把结果缩小范围到1(苹果)或0(香蕉)

感知机怎么来正确分类?(通过代码假数据引入)
import matplotlib.pyplot as plt
import numpy as np
# 定义正确的输入和输出 x 表示颜色(黄--->红), y 表示形状(方形-->圆形)
test_inputs = [(0,0),(0,1),(1,0),(1,1)]
# 定义正确的结果 1 表示苹果, 0 表示香蕉
correct_outputs = [0,0,0,1]
# 随机指定3个数
weight1 = 0.8
weight2 = 0.8
bias = -0.5
# 方程 :weight1 * x1 + weight2 * x2 + bias = 0
X = np.linspace(-5,5,10)
Y = -(weight1*X + bias)/weight2
# 画图
fig = plt.figure(figsize=(5,5),dpi=100)
plt.xlim(-1,4)
plt.xlabel("yellow--->red")
plt.ylim(-1,4)
plt.ylabel("rect--->circle")
# 绘制一条直线
plt.plot(X,Y)
for index,item in enumerate(test_inputs):
# 为了方便观察数据,当它为苹果的时候,图标显示红色
if correct_outputs[index] == 1:
plt.scatter(item[0],item[1],c="red")
else:
plt.scatter(item[0],item[1],c="yellow")
plt.show()
# 激活函数
def activateFunction(value):
if value > 0:
return 1
else:
return 0
for index,item in enumerate(test_inputs):
# 根据公式测试预测值
result = weight1 * item[0] + weight2 * item[1] + bias
# 调用激活函数 如果跟真实结果一样就是分类成功
if(activateFunction(result) == correct_outputs[index]):
print("分类成功,预测结果和真实结果一样")
else:
print("分类失败")
(0,1)和(1,0)两个点没有分类成功:
2. 得出感知机决策边界线的移动过程:
0.8 x 1 + 0.8 x 2 − 0.5 = 0 0.8x_1 + 0.8x_2 - 0.5 = 0 0.8x1+0.8x2−0.5=0 这条直线需要靠近坐标(0,1)和(1,0)
原函数先减去(0,1,1) 让直线靠近(0,1)坐标点,第三个数字1是为了给b补位
( 0.8 − 0 ) x 1 + ( 0.8 − 1 ) x 2 + ( − 0.5 − 1 ) = 0 (0.8 - 0)x_1 + (0.8 - 1)x_2 + (-0.5 -1) = 0 (0.8−0)x1+(0.8−1)x2+(−0.5−1)=0
0.8 x 1 − 0.2 x 2 − 1.5 = 0 0.8x_1 - 0.2x_2 - 1.5 = 0 0.8x1−0.2x2−1.5=0
感知机的过程就是一直循环这个操作,使得m1、m2和b的值找到最优解
移动决策边界
-
如果点(p,q) 分类正确, 什么事都不做
-
如果点(p,q) 分类不正确
-
分类结果为香蕉,实际是苹果. 点在线的下方, 线往上移.学习速率 α \alpha α, ( w 1 , w 2 , b ) (w_1,w_2,b) (w1,w2,b)减去( α p \alpha p αp, α q \alpha q αq, α ∗ 1 \alpha*1 α∗1)
( w 1 w_{1} w1= w 1 w_{1} w1- α p \alpha p αp, w 2 w_{2} w2= w 2 w_{2} w2- α q \alpha q αq,b=b- α \alpha α*1) -
分类为苹果, 实际是香蕉. 点在线的上方,线往下移. 学习速率 α \alpha α,
( w 1 w_1 w1, w 2 w_2 w2,b)加上( α p \alpha p αp, α q \alpha q αq, α \alpha α*1)
( w 1 w_{1} w1= w 1 w_{1} w1+ α p \alpha p αp, w 2 w_{2} w2= w 2 w_{2} w2+ α q \alpha q αq,b=b+ α ∗ 1 \alpha*1 α∗1) -
更新w1、w2和b的值
-
猜测中间值为(0.5,0.5)
-
根据公式线往下移
w1' = w1 + α * 0.5
w2' = w2 + α * 0.5
b' = b + α * 1
# 实现感知机
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt("data_ganziji.csv",delimiter=",")
# 数据中香蕉和苹果点的x坐标和y坐标
X = data[:,0:2]
# 数据第三列为分类 香蕉or苹果
Y = data[:,2:3]
# 创建自定义 规定大小
fig = plt.figure(figsize=(5,5),dpi=80)
# 遍历数据的长度
for i in range(len(Y)):
# 如果第三列是0那么就是香蕉
if Y[i] == 0 :# 香蕉
# 根据坐标画出黄色点
plt.scatter(X[i][0],X[i][1],c="yellow")
else:
# 反之画出红色点
plt.scatter(X[i][0],X[i][1],c="red")
# 随机w1和w2的值
np.random.seed(42)
W = np.random.rand(2,1)
b = -1
w1 = W[0,0]
w2 = W[1,0]
# 创建线的x坐标
XX = np.linspace(-2,2,10)
# 根据公式求y坐标 m1 * x2 + m2 * x2 + b = 0
YY = -(w1*XX + b)/w2
# 画出散点图和决策边界线
plt.plot(XX,YY)
plt.xlim(0,1)
plt.ylim(0,1)
# 定义学习率
learning_rate = 0.01
# 更新w1、w2和b的值 猜测中间值为(0.5,0.5) 根据公式线往下移 w1' = w1 + α * p
w1 = w1 + learning_rate * 0.5
w2 = w2 + learning_rate * 0.5
b = b + learning_rate * 1
YY2 = -(w1 * XX +b) / w2
plt.plot(XX,YY2)
plt.show()
这时候看到决策边界线确实正在往中间前进,只需要一直循环,直到决策边界线拟合到一个完美的位置。
感知机实现
实现步骤:
- 随机出w1、w2变量和自定义b变量
- 遍历所有数据,使用当前的w1、w2和b变量套用公式进行计算
- 把算出的结果放入激活函数
- 如果大于0直接为1,小于0就为0
- 为1的是一类 为0的是一类
- 判断使用当前w1、w2和b变量计算出的分类和真实值是否一样
- 如果一样就什么都不用做
- 如果不一样,判断决策边界线是该往上移动还是往下移动
- 往上移动使用减法公式 往下移动使用加法公式
- 更新各变量的值
- 重复2和3的步骤直到决策边界线能做出正确的分类
- 可以画散点图和线图查看决策边界是否收敛到一个合适的位置
# 实现感知机
import numpy as np
import matplotlib.pyplot as plt
# 加载数据
data = np.loadtxt("data_ganziji.csv",delimiter=",")
# 数据中香蕉和苹果点的x坐标和y坐标
X = data[:,0:2]
# 数据第三列为分类 香蕉or苹果
Y = data[:,2:3]
# 创建自定义画图窗口 规定大小
fig = plt.figure(figsize=(5,5),dpi=80)
# 遍历数据的长度
for i in range(len(Y)):
# 如果第三列是0那么就是香蕉
if Y[i] == 0 :# 香蕉
# 根据坐标画出黄色点
plt.scatter(X[i][0],X[i][1],c="yellow")
else:
# 反之画出红色点
plt.scatter(X[i][0],X[i][1],c="red")
# 随机w1和w2的值
np.random.seed(42)
W = np.random.rand(2,1)
b = -1
# 创建线的x坐标
XX = np.linspace(-2,2,10)
plt.xlim(0,1)
plt.ylim(0,1)
def step_func(value):
"""
激活函数 如果大于0就输出1 反之输出0 (0为香蕉,1为苹果)
@param value: 用w1、w2和b的值算出来的分类 如果大于0就是在决策边界线上面,反之在决策边界下面,用来判断是香蕉还是苹果
@return: 返回1或0(0为香蕉,1为苹果)
"""
if value >= 0:
return 1
else:
return 0
def perception(X,W,b):
"""
检测函数
@param X: 数据中每一个点的x坐标和y坐标
@param W: 随机出来的w1变量和w2变量
@param b: 自定义的b变量
"""
# 矩阵相乘 y分类 = w1 * x1 + w2 * x2 + b
value = (np.matmul(X,W) + b)[0]
# 调用激活函数 把激活函数的返回值返回
return step_func(value)
def perceptronStep(X,Y,W,b,learning_rate):
"""
修改参数函数
@param X: 数据中每一个点的x坐标和y坐标的二维数组
@param Y: 数据的分类 (0为香蕉,1为苹果)
@param W: 随机出来的w1变量和w2变量
@param b: 自定义的b变量
@param learning_rate: 学习率
"""
# 有多少条数据遍历多少次
for i in range(len(X)):
# 调用检测函数 使用目前的w1、w2和b的值进行分类
y_pred = perception(X[i],W,b)
# 获取到真实值
y_real = Y[i]
# 如果真实值为1 预测值为0
# 检测的为香蕉 真实为苹果 线在当前点的上方 往下移动 使用加法
if y_real - y_pred == 1:
# 使用公式修改w1、w2和b的值
# w1' = w1 + x1 * learning_rate
W[0] += X[i,0] * learning_rate
# w2' = w2 + x2 * learning_rate
W[1] += X[i,1] * learning_rate
# b' = b + learning_rate * 1
b += learning_rate *1
# 反之 线在当前点的下方 往上移动 使用减法
elif y_real - y_pred == -1:
W[0] -= X[i,0] * learning_rate
W[1] -= X[i,1] * learning_rate
b -= learning_rate *1
else: # 如果真实值和预测值相等 什么都不用干
pass
# 把更新后的W变量和b变量返回
return W,b
def trainPerceptron(X,Y,W,b,learning_rate,num_epochs):
"""
训练函数
@param X: 数据中每一个点的x坐标和y坐标的二维数组
@param Y: 数据的分类 (0为香蕉,1为苹果)
@param W: 随机出来的w1变量和w2变量
@param b: 自定义的b变量
@param learning_rate: 学习率
@param num_epochs: 学习次数 纪元
"""
# 用于存放训练完成之后的变量
w1,w2,f_b = 0,0,0
# 遍历学习次数
for i in range(num_epochs):
# 调用修改参数的函数
W,b = perceptronStep(X,Y,W,b,learning_rate)
w1 = W[0]
w2 = W[1]
f_b = b
return w1,w2,f_b
# 获取到训练完的参数
w1,w2,f_b = trainPerceptron(X,Y,W,b,learning_rate=0.01,num_epochs=30)
# 使用参数预测分类
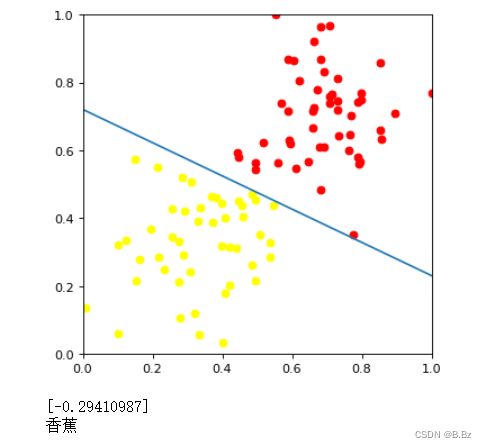
a = w1 * 1 + w2 * 0.4 + b
print(a)
if a[0]<0:
print('香蕉')
elif a[0] > 0:
print('苹果')
为什么是神经网络基础?
- 实现一个感知机就是实现了单个神经元
- 接收到输入 ➡ 神经元内计算 ➡ 修改变量把结果输出
- 神经网络就是多个感知机结合在一起