Leetcode哈希表题目

以下为Datawhale Leetcode开源学习思路总结，以下代码均为Leetcode代码，但不一定是最优解，仅供参考学习。

上图参考Carl哥的代码随想录官网，附上参考链接

217. 存在重复元素

C++中数据结构unordered_set有去重功能，本题遍历nums，将每个元素加入到unordered_set中即可，当每次新加入时首先在unordered_set中查找，找到的话说明有重复，返回false，否则返回true。思路较为简单。

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        unordered_set<int> s;
        for(int i = 0; i < nums.size(); ++i) {
            if(s.find(nums[i]) != s.end()) {
                return true;
            } else {
                s.insert(nums[i]);
            }
        }
        return false;
    }
};

219. 存在重复元素II

本题需要用unordered_map分别记录当前元素值以及其出现的位置idx，然后加入到哈希表中，当遍历nums时，第二次出现某元素在哈希表中时，计算其位置是否 <= k，成立则返回true，否则更新该元素的位置mp[nums[i]] = i。思路简单。

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        int dis = 0;
        for(int i = 0; i < nums.size(); ++i) {
            if(mp.find(nums[i]) == mp.end()) {
                mp[nums[i]] = i;
            } else {
                if(abs(mp[nums[i]]- i) <= k) {
                    return true;
                }
                mp[nums[i]] = i;
            }
        }
        return false;
    }
};

36. 有效的数独

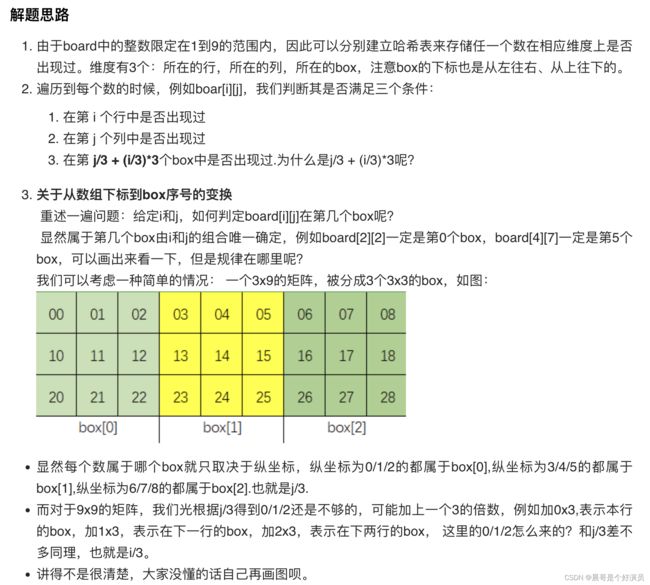
需要注意的重点是：j/3 + (i/3)*3，可以划分具体的小块，每3x3的方格为一个box，具体代码实现如下，很清晰：

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        int row[9][10] = {0};
        int col[9][10] = {0};
        int box[9][10] = {0};

        for(int i = 0; i < 9; ++i) {
            for(int j = 0; j < 9; ++j) {
                if(board[i][j] == '.') continue;
                int num = board[i][j] - '0';
                if(row[i][num]) return false;
                if(col[j][num]) return false;
                if(box[j/3+(i/3)*3][num]) return false;

                row[i][num] = 1;
                col[j][num] = 1;
                box[j/3+(i/3)*3][num] = 1;
            }
        }
        return true;
    }
};

349. 两个数组的交集

这道题的思路是，向哈希表中加入一个数组，然后遍历另一个数组，找他是否在哈希表中出现过，若出现过，将该值加入到要返回结果的新的哈希结构中。我的代码还想考虑字符串长度的影响，但是发现好像没啥影响，知道思路即可。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        int n1 = nums1.size();
        int n2 = nums2.size();
        unordered_set<int> res;
        unordered_set<int> tmp;
        if(n1 < n2) {
            for(int i = 0; i < n1; ++i) { tmp.insert(nums1[i]); }
            for(int i = 0; i < n2; ++i) {
                if(tmp.find(nums2[i]) != tmp.end()) { res.insert(nums2[i]); }
            }
        } else {
            for(int i = 0; i < n2; ++i) { tmp.insert(nums2[i]); }
            for(int i = 0; i < n1; ++i) {
                if(tmp.find(nums1[i]) != tmp.end()) { res.insert(nums1[i]); }
            }
        }
        return vector<int>(res.begin(), res.end());
    }
};

还有一种做法是使用C++ STL求交集的库函数，求交集之前对其进行由小到大排序，然后back_inserter中传入求完交集后保存结果的vector容器，只需要从中去重即可。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        vector<int> res;
        set_intersection(nums1.begin(), nums1.end(), nums2.begin(), nums2.end(), back_inserter(res));
        unordered_set<int> s;
        for(auto x : res)
            s.insert(x);
        vector<int> res1;
        for(auto x : s)
            res1.push_back(x);
        return res1;
    }
};

350. 两个数组的交集II

这题如果用C++ STL直接就可以得出结论，相比349题，区别在于这题不需要去重。如果按照一般做法，需要记录其中一个集合的数字出现的频率，然后遍历另一个即可，并在前一个集合中找，找到的话减少1点频率，若频率为0了，就不保存遍历另一个集合中的当前值了，代码如下：

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        int n1 = nums1.size();
        int n2 = nums2.size();
        unordered_map<int, int> mp;
        vector<int> res;
        if(n1 < n2) {
            for(int i = 0; i < n1; ++i)
                ++mp[nums1[i]];

            for(int i = 0; i < n2; ++i) {
                if(mp.find(nums2[i]) != mp.end() && mp[nums2[i]] > 0) {
                    res.push_back(nums2[i]);
                    --mp[nums2[i]];
                }
            }
        } else {
            for(int i = 0; i < n2; ++i)
                ++mp[nums2[i]];

            for(int i = 0; i < n1; ++i) {
                if(mp.find(nums1[i]) != mp.end() && mp[nums1[i]] > 0) {
                    res.push_back(nums1[i]);
                    --mp[nums1[i]];
                }
            }
        }
        return res;
    }
};

下面给出STL中求交集的代码：

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        vector<int> res;
        set_intersection(nums1.begin(), nums1.end(), nums2.begin(), nums2.end(), inserter(res, res.begin()));
        return res;
    }
};

706. 设计哈希映射

题解有人直接用红黑树实现，就不讨论了，这里贴出最简单的，直接数组实现：

class MyHashMap {
public:
    MyHashMap() {}
    
    void put(int key, int value) {
        mp[key] = value;
    }
    
    int get(int key) {
        return mp[key];
    }
    
    void remove(int key) {
        mp[key] = -1;
    }
private:
    vector<int> mp = vector<int>(1e6+1, -1);
};