林轩田-机器学习基石-作业4-python源码

正则化线性回归（regularized linear regression）和验证（validation）的实验

对于正则化线性回归下的分类问题，我们有Wreg = arg min( λ/N * ||W||^2 + 1/N * ||XW-Y||^2 )

以下问题均基于

## 训练集：http://www.csie.ntu.edu.tw/~htlin/course/ml15fall/hw4/hw4_train.dat
## 测试集：http://www.csie.ntu.edu.tw/~htlin/course/ml15fall/hw4/hw4_test.dat

因为以下问题均为分类问题，所以Eout按照0/1error来计算

问题13：当λ = 11.26时，相应的Ein和Eout是多少？

根据课堂上的推导，我们求得了Wreg = （Xt*X + λI）^-1*XtY，所以该问题只需要把相应的λ代入求Wreg，然后再计算Ein和Eout就好

import numpy as np
import matplotlib.pyplot as plt

### import training data or testing data
def data_load(path):
    ### open data file and read all lines
    f = open(path)
    try:
        lines = f.readlines()
    finally:
        f.close()

    ### create return data structure
    example_num = len(lines)
    feature_dimension = len(lines[0].strip().split())  ### how to get dimension by the easier way
    X = np.zeros((example_num, feature_dimension))
    Y = np.zeros((example_num, 1))
    X[:,0] = 1

    ### parse every line
    for index,line in enumerate(lines):
        ### get features
        items = line.strip().split()
        X[index,1:] = [float(_) for _ in items[:-1]]
        Y[index] = float(items[-1])

    return X,Y

因为是二维特征，满足一下好奇心，画散点图看看样本点的分布情况(为了让显示清晰，我绘制了两幅图，第二幅图显示了正负类交界处的情况)
我们可以使用plt.scatter(x, y, s=area1, marker=’^’, c=c)函数来绘制散点图，其中

X–横坐标

Y–纵坐标

S–每个坐标的大小

marker–标记的形状

c–标记的颜色

def data_visual(X, Y, title="Default", xmin=0, xmax=1, ymin=0, ymax=1, func=False, w=[]):
    x1 = X[:,1]
    x2 = X[:,2]
    labels = Y[:,0]

    ### get size array
    dot_size = 20
    size = np.ones((len(x1)))*dot_size

    ### get masked size array for positive points(mask the negative points)
    s_x1 = np.ma.masked_where(labels<0, size)
    ### get masked size array for positive points(mask the positive points)
    s_x2 = np.ma.masked_where(labels>0, size)

    ### plot positive points as x
    plt.scatter(x1, x2, s_x1, marker='x', c='r', label="positive")
    ### plot negative points as o
    plt.scatter(x1, x2, s_x2, marker='o', c='b', label="negative")

    ### plot func if require
    if func:
        x1_dot = np.arange(xmin,xmax,0.01)
        x2_dot = np.arange(ymin,ymax,0.01)
        x1_dot,x2_dot = np.meshgrid(x1_dot, x2_dot)

        f = w[0,0] + w[1,0]*x1_dot + w[2, 0]*x2_dot
        plt.contour(x1_dot, x2_dot, f, 0)

    ### add some labels
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.title(title)
    plt.legend()

    plt.xlim(xmin, xmax)
    plt.ylim(ymin, ymax)

    plt.show()

### load and plot training data
X_train,Y_train = data_load('hw4_train.dat')
data_visual(X_train, Y_train, "Example data")
data_visual(X_train, Y_train, "Partial Example data", 0.45,0.55,0.45,0.55)

求解Ein和Eout，求出来可得Ein=0.055 Eout=0.052.

第一次看到结果，我是感到比较诧异的。因为如果根据上面的样本的可视化图片，如果用linear regression来拟合的话按理来说应该会拟合一条穿过所有点的直线（linear regression采用的是squared error的cost function，穿过所有点的直线的squared error应该是最小的），而不应该是下图中的那条直线。但是细想，哦，这不就是regularization的作用吗，我们的L2regularizer对我们的参数的||W||^2做了限制，λ=11.26（估计是某个纪念日吧，只有林老师才知道），这个λ是一个很大的数字，同时也意味着对W的限制很严格，所以我们才得到了那么一条‘意料之外’的直线。然后我又多试了几个λ值。（读者可自行拷贝代码然后运行）

在λ = 11.26 的时候，拟合出来的参数向量是[-0.88765371, 1.00531461, 1.00530077]

在λ = 1 的时候，拟合出来的参数向量是[-1.42004196, 1.48896417, 1.48882476]

在λ = 0.01 的时候，拟合出来的参数向量是[-1.5033133, 1.63252051, 1.49578124]

在λ = 0 的时候，拟合出来的参数向量是[-1.49776048e+00, 3.67237446e+03, -3.66924721e+03]

由此可见，当我们的λ由大变小的时候，算法对W向量的限制也越来越低（表现为||W||^2越来越大），当λ=0时，对W无限制，就拟合出来我们心中认为最合理的那条穿过所有样本点的直线

class LinearRegressionReg:

    def __init__(self):
        self._dimension = 0

    def fit(self, X, Y, lamb):
        self._dimension = len(X[0])
        self._w = np.zeros((self._dimension,1))
        self._lamb = lamb
        self._w = np.linalg.inv(np.dot(X.T, X) + lamb*np.eye(self._dimension)).dot(X.T).dot(Y)

    def predict(self, X):
        result = np.dot(X, self._w)
        return np.array([(1 if _ >= 0 else -1) for _ in result]).reshape(len(X), 1)

    def score(self, X, Y):
        Y_predict = self.predict(X)
        return sum(Y_predict!=Y)/(len(Y)*1.0)

    def get_w(self):
        return self._w

    def print_val(self):
        print "w: ", self._w

### Error in
lr = LinearRegressionReg()
lr.fit(X_train, Y_train, 11.26)
Ein = lr.score(X_train, Y_train)
data_visual(X_train, Y_train, title="Training Data", xmin=0.4, xmax=0.6, ymin=0.35, ymax=0.6, func=True, w=lr.get_w())
lr.print_val()
print "Ein : ", Ein

### Error out
X_test, Y_test = data_load('hw4_test.dat')
Eout = lr.score(X_test, Y_test)
data_visual(X_test, Y_test, title="Test Data", xmin=0.4, xmax=0.6, ymin=0.35, ymax=0.6, func=True, w=lr.get_w())
print "Eout : ", Eout

w:  [[-0.88765371]
 [ 1.00531461]
 [ 1.00530077]]
Ein :  [ 0.055]

Eout :  [ 0.052]

问题14/15：画出λ在分别取值{ 10^2, 10^1, 10^0……10^-8, 10^-9, 10^-10}时的Ein的曲线图，分别求出Ein最小时的λ和Eout最小时的λ（Ein或者Eout相同时，取最大的λ）

### get lambs
log_lambs = range(2, -11, -1)
lambs = [10**_ for _ in range(2, -11, -1)]
Ein = []
Eout = []
lr = LinearRegressionReg()

### get Ein and Eout array
for index,lamb in enumerate(lambs):
    ### fit models
    lr.fit(X_train, Y_train, lamb)

    ### get Ein
    Ein.append(lr.score(X_train, Y_train))

    ### get Eout
    Eout.append(lr.score(X_test, Y_test))

### plot Ein and Eout curve
plt.plot(log_lambs, Ein, label="Error In", marker='o')
plt.plot(log_lambs, Eout, label="Error Out", marker='o')

plt.title("Curve of Error")
plt.xlabel("Log lambda")
plt.ylabel("Error")
plt.legend()
plt.show()

print ("λ = %e with minimal Ein: %f"%(lambs[Ein.index(min(Ein))], min(Ein)))
print ("λ = %e with minimal Eout: %f"%(lambs[Eout.index(min(Eout))], min(Eout)))

λ = 1.000000e-08 with minimal Ein: 0.000000
λ = 1.000000e-02 with minimal Eout: 0.021000

接下来的问题和validation有关。将我们的样本分为训练集（120）和测试集（80），将所有的模型（不同的lambda值）在训练集上训练，然后讲得出的假设在测试集上验证

问题16/17：single validation

求出所有λ对应的Etrain,Eval,Eout,分别找出最小Etrain的λ和最小Eval的λ

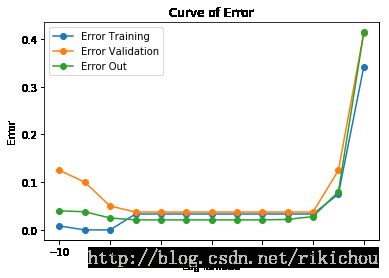
从下面的结果以及图片可以看出

1，Etrain,Eval,Eout的三条曲线整体趋势一致，也符合我们课堂上的结论。

2，根据Etrain选出来的结果比Eval选出来的结果好那么一点点，其实也差不多。λ=1.000000e-08时的Eout最小，所以说根据Eval来选择并不是总优于Etrain？？

### get train set and test set
X,Y = data_load('hw4_train.dat')

X_tra = X[0:120,:]
Y_tra = Y[0:120,:]

X_val = X[120:,:]
Y_val = Y[120:,:]

### 
log_lambs = range(2, -11, -1)
lambs = [10**_ for _ in range(2, -11, -1)]
Etrain = []
Eout = []
Eval = []

lr = LinearRegressionReg()

### get Etrain and Eval and Eout array
for index,lamb in enumerate(lambs):
    ### fit models
    lr.fit(X_tra, Y_tra, lamb)

    ### get Etrain
    Etrain.append(lr.score(X_tra, Y_tra))

    ### get Eval
    Eval.append(lr.score(X_val, Y_val))

    ### get Eout
    Eout.append(lr.score(X_test, Y_test))

### plot Ein and Eval and Eout curve
print len(Ein)
print len(log_lambs)
plt.plot(log_lambs, Etrain, label="Error Training", marker='o')
plt.plot(log_lambs, Eval, label="Error Validation", marker='o')
plt.plot(log_lambs, Eout, label="Error Out", marker='o')

plt.title("Curve of Error")
plt.xlabel("Log lambda")
plt.ylabel("Error")
plt.legend()
plt.show()

print ("λ = %e with minimal Etrain: %f, Eout: %f"%(lambs[Etrain.index(min(Etrain))], min(Etrain),\
                                                  Eout[Etrain.index(min(Etrain))]))
print ("λ = %e with minimal Eval: %f, Eout: %f"%(lambs[Eval.index(min(Eval))], min(Eval),\
                                                Eout[Eval.index(min(Eval))]))

39
13

λ = 1.000000e-08 with minimal Etrain: 0.000000, Eout: 0.025000
λ = 1.000000e+00 with minimal Eval: 0.037500, Eout: 0.028000

18题：根据16/17题选出的λ（1.000000e-08），利用所有的样本来训练该λ对应的模型，求Ein和Eout

结果显示，使用整体样本训练出来的最优模型的Eout比仅使用Etrain训练出来的最优模型的Eout要小一些

### load data
X_train,Y_train = data_load('hw4_train.dat')

### fit model use 
lr = LinearRegressionReg()
lr.fit(X_train, Y_train, 1.000000e-08)

Ein = lr.score(X_train, Y_train)
Eout = lr.score(X_test, Y_test)

print "Error in : ", Ein
print "Error out: ", Eout

Error in :  [ 0.015]
Error out:  [ 0.02]

接下来的内容是cross validation。我们将样本平均分为5份，每份有40个样本

19题：使用交叉验证，得出Ecv最小的λ

### get train set and test set
X,Y = data_load('hw4_train.dat')

### 
log_lambs = range(2, -11, -1)
lambs = [10**_ for _ in range(2, -11, -1)]
Ecv = []

lr = LinearRegressionReg()

num = len(Y)
fold = 5
size = num/fold
Ecv = []
### get Etrain and Eval and Eout array
for index,lamb in enumerate(lambs):
    Err = []
    for index,i in enumerate(np.arange(0,num,size)[0:fold]):
        start = index*size
        end = (index+1)*size if index+1 < fold else num
        ### print "start: ",start," end: ", end

        X_test = X[start:end]
        X_val = np.concatenate((X[:start],X[end:]))

        Y_test = Y[start:end]
        Y_val = np.concatenate((Y[:start],Y[end:]))

        ### fit models
        lr.fit(X_test, Y_test, lamb)

        ### get Err
        Err.append(lr.score(X_val, Y_val))

    ### get Ecv
    Ecv.append(sum(Err)/(len(Err)*1.0))

plt.plot(log_lambs, Ecv, label="Ecv", marker='o')
plt.title("Error Cross Validation")
plt.xlabel("Log lambda")
plt.ylabel("Error")
plt.legend()
plt.show()

print ("λ = %e with minimal Ecv: %f"%(lambs[Ecv.index(min(Ecv))], min(Ecv)))

λ = 1.000000e-03 with minimal Ecv: 0.033750

19题：根据18题得到的模型（λ=1.000000e-03），将模型在整个训练集上进行训练，然后在测试集上进行测试，得出Ein和Eout

### get train set and test set
X,Y = data_load('hw4_train.dat')
X_test,Y_test = data_load('hw4_test.dat')

lr = LinearRegressionReg()
lr.fit(X, Y, 1.000000e-03)
Ein = lr.score(X, Y)
Eout = lr.score(X_test, Y_test)

print "Ein: ", Ein
print "Eout: ", Eout

Ein:  [ 0.03]
Eout:  [ 0.016]