Coursera self-driving car Part1 Final Project——自动驾驶轨迹跟踪之Stanley算法推导及Python实现

Coursera self-driving car Part1 Final Project——自动驾驶轨迹跟踪之Stanley算法推导及Python实现

同样，该Stanley算法也是用于Coursera self driving car Part1 FinalProject里得横向控制，纵向采用PID控制不赘述。

1.Stanley算法原理

Stanley算法原理相对比较简单，可以处理初始横向误差，航向误差较大得情况。

Stanley控制量前轮转角得产生由两部分构成：

为了消除车辆航向与参考航向之间得角度差所需得前轮转角，参考航向即为参考点得切线方向

为了消除横向距离需要得前轮转角

       

 为 我们给定的距离，但如果设定为一个常值，越小，车子就越快接近参考路径，转向角就越大。低速时可能适用，高速时就使车辆变得非常激进，使得系统出现振荡，因此我们通常将其设定为一个与v正比的值

 

这个比例系数k越大， 就越小，车辆就越激进。k作为Stanley控制器的一个参数，类似与PID的比例控制，还可以进行改造加入微分积分环节，这里不再赘述。

原理就是这样，很简单。

2.Coursera self driving car Part1 FinalProject介绍

Part1 FinalProject参见我得另一篇博客里的2.1小节

Coursera self-driving car Part1 Final Project——无人车轨迹跟踪之MPC模型预测控制原理推导及Python实现

3.Python实现

这里只介绍关键代码的实现.

这个Final project里的设定是提供的waypoints是一个点集，每个时刻都会更新，详见本博客第2小节。waypoints理解为接下来racetrack_waypoints.txt里的几个参考点进行线性插值后的点集。

算法代码实现大致流程：

参数初始化→找到当前最近点与最近距离(横向误差)→计算参考航向→判断横向误差符号→计算→下发控制量

3.1 找到附近小段轨迹中的距离车辆的最近点

思路就是遍历waypoints小段轨迹点集，依次求出距离，初始最近距离设置为无穷大，最近点索引为0，然后后面若发现有更小的距离，则更新最近距离min_dist和最近点索引 min_idx。

#找到最近的路径点索引
            min_idx       = 0
            min_dist      = float("inf")
            for i in range(len(self._waypoints)):          
               dist = np.linalg.norm(np.array([
                    self._waypoints[i][0] - x_f,
                    self._waypoints[i][1] - y_f]))   #出现“Unexpected indent”原因可能之一，可能是你的函数或哪一行的缩进出了问题，if 跟dist缩进一样的属于for循环下
               if dist < min_dist:               #每个i比较是否比min_dist要小，将if放错位置缩进不对顶格导致每次都取了最后一个i，因为无论距离多少肯定比inf小导致控制量很大原地转圈
                        min_dist = dist
                        min_idx = i 

3.2 参考航向的计算

Final project的设定是车辆的实际状态x,y,phi,v都会由传感器给出数值，实际航向角（车速方向与x轴所成角，-pi-pi）为yaw，但是如上原理所述Stanley算法中要用到参考航向角。

参考航向角的计算思路：

程序中跟踪路径横向控制时是将路径距车辆最近点作为参考点，这里将最近点与其下一个点的连线方向作为参考航向(若最近点是点集中的最后一个点，则采用最近点上一个点与最近点的连线作为参考航向)，代码如下：

atan2计算出来的角度会自动转换到-pi到pi，航向角的设定就是-pi到pi

#设定目标点
            tx=waypoints[min_idx][0]
            ty=waypoints[min_idx][1]
            #判断用下一个点还是上一个点与当前目标点的连线作为参考航向
            ##重要！！！因为yaw 这里定义的范围是有负值的而不是0-2pi，是-pi到pi，那么th也-pi到Pi即可，否则有问题
            if min_idx

3.3 判断横向误差的符号

看了几个CSDN上的排在前面的答案，移植到python中做这个FinalProject时，发现都是有漏洞的，用来做这个project经常冲出跑道。看的几个博客常见的一种思路，就是：

简单的把车在参考点切线的右侧(Axr+Byr+C>0)作为负(Coursera Finalproject里定义向左转为负的转向角)，车子在在参考点切线的左侧(Axr+Byr+C<0)作为正，简单的这样判断方向，当同一段轨迹，小车是向右上方运动时，Ax+By+C>0左转还没错，

当小车是反向向左下方跟踪轨迹时，Ax+By+C>0左转就有问题了，反而偏离了轨迹。

下面介绍一种在Github上看到的新方法。

用参考路径的第一个参考点P0与小车位置P的连线与x轴所成角,最近参考点的切线方向的航向角，这种角度均在-pi到pi之间，航向角是-pi-pi，atan2计算出来的角度也是-pi到pi。

上图如果小车向右上方运动，左拐没问题，横向误差为负。

如果小车向左下方运动，

小车需向右拐，则横向误差为正，也正确。

在Finalproject里坐标系是反的，则上述规则刚好反过来即可。

代码如下：

#判断error的符号
            #计算第一个参考点到当前位置的连线与x轴所成角
            yaw_cross_track = np.arctan2(y_f-waypoints[0][1], x_f-waypoints[0][0])
            #waypoints里的第一个点到当前位置连线角度与参考航向之间的夹角计算
            yaw_path2ct = th - yaw_cross_track
            if yaw_path2ct > np.pi:
                yaw_path2ct -= 2 * np.pi
            if yaw_path2ct < -np.pi:
                yaw_path2ct += 2 * np.pi
            # yaw_path2ct>0就是正的
            if yaw_path2ct > 0:
               error = abs(error)
            else:
               error = - abs(error)
            #

3.4 角度加减后范围的限制

整个程序里的角度范围都是-pi到pi，无论是航向角还是求反正切出来的值，

但是两个角度加减后可能超出范围，都要转化到这个范围内。代码如下：

#waypoints里的第一个点到当前位置连线角度与参考航向之间的夹角计算
            yaw_path2ct = th - yaw_cross_track
            if yaw_path2ct > np.pi:
                yaw_path2ct -= 2 * np.pi
            if yaw_path2ct < -np.pi:
                yaw_path2ct += 2 * np.pi

3.5 运行结果

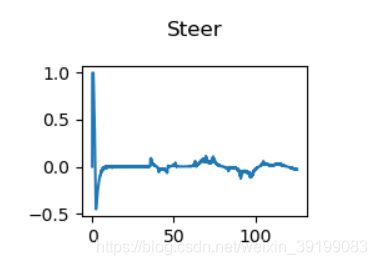
与我另外两篇博客介绍的Pure Pursuit纯跟踪, MPC横向控制并没有看出明显优劣，因为参数的设置相对都比较随意。但是都能够很好的完成轨迹跟踪的任务。

运行视频链接

https://www.bilibili.com/video/BV1kB4y1F7sU

源码链接
https://download.csdn.net/download/weixin_39199083/18814608