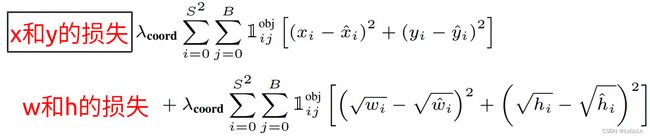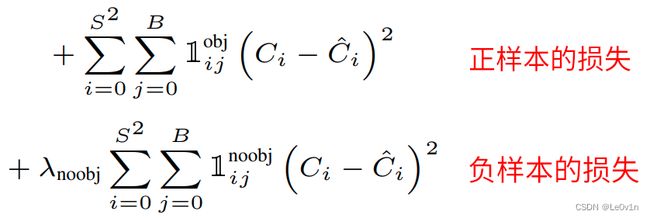①YOLO v1~v3、②YOLO v3 SPP、③IoU、GIoU、DIoU、CIoU、④Focal Loss的理论讲解
0. 引言
0.1 安排
- YOLO v1 (简单理论)
- YOLO v2 (简单理论)
- YOLO v3 (详细理论)
- YOLO v3 SPP (trick扩充 + 代码讲解)
- IoU、GIoU、DIoU、CIoU
- Focal Loss
0.2 学习代码的步骤
- 搜该网络的讲解 —— 大概有一个印象
- 读原文(非常重要) —— 很多细节都是通过原论文实现的 —— 发现更多原来没有发现的知识点
- 读代码 —— github官方代码/复现的源码(⭐️多的)
- 根据作者的
README.md将代码跑通 —— 跑通只是第一步而不是最后一步 - 分析网络搭建的部分 —— 结合原论文,还是比较好理解的
- 分析数据预处理和损失计算这两大部分 —— 不要小看这两大部分,比网络搭建有难度
- 网络搭建、数据预处理和损失计算看完之后,基本上就掌握了这个网络的核心技术点
- 看代码的过程中是需要结合原论文进行参考的。在读原论文的时候,有些地方是不太好理解的,而结合代码就可以进一步理解之前很难理解的部分
- 根据作者的
1. YOLO v1
论文题目:You Only Look Once: Unified, Real-Time Object Detection
论文地址:https://arxiv.org/abs/1506.02640

YOLO是目标检测One-stage的经典网络。YOLO v1:
- 2016年CVPR发表的论文
- PASCAL 2007的mAP为63.4%(SSD为74.3%,Faster R-CNN为73.2%)
- 输入图片大小为448×448,推理速度为45 FPS (SSD为300×300,59FPS)
YOLO v1在mAP上比不过同年的SSD和之前的Faster R-CNN
在速度上秒杀Faster R-CNN,但打不过同年的SSD
YOLO v1相比同年发布的SSD是没有什么优势的
1.1 核心思想
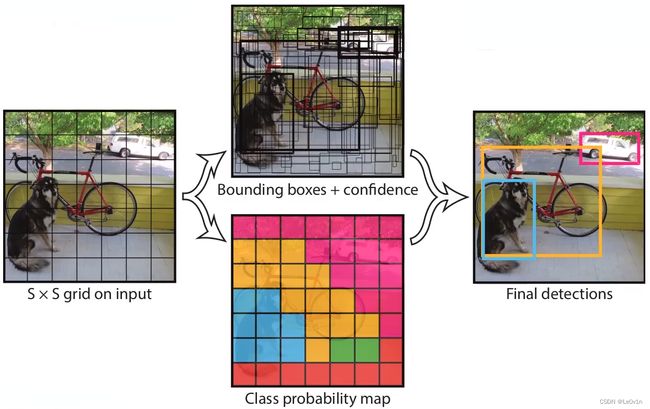
1.2 第一步:划分grid cell
将输入图片分为 7×7个网格(grid cell),如果某个目标GTBox的中心落在这个网格当中,则这个网络就负责预测这个目标。
1.3 第二步:每个grid cell需要做的事情
每个网络(grid cell)要预测2个BBox (Bounding Box),每个BBox要预测目标的位置信息( x , y , w , h x,y,w,h x,y,w,h)之外还要预测一个confidence值(目标分类值,和类别没关系,是IoU×一个系数,是一个数)。每个网络还需要预测C个类别分数(是一个向量[num_classes, ])。
( x , y ) (x,y) (x,y):相对grid cell的目标边界框 —— 相对值 (grid cell) ∈ [ 0 , 1 ] \in [0, 1] ∈[0,1]
( w , h ) (w, h) (w,h):相对整张图片的宽度和高度 —— 相对值 (image) ∈ [ 0 , 1 ] \in [0, 1] ∈[0,1]
confidence:预测框与GTBox的IoU值,再乘 Pr(Object) \text{Pr(Object)} Pr(Object)。
其中,
Pr(Object) = { 1 网 格 中 确 实 存 在 目 标 ( with GT ) 0 网 格 中 不 存 在 目 标 ( without GT ) \text{Pr(Object)} =\begin{cases} 1 & 网格中确实存在目标(\text{with GT}) \\ 0 & 网格中不存在目标(\text{without GT}) \end{cases} Pr(Object)={10网格中确实存在目标(with GT)网格中不存在目标(without GT)
Note:
- YOLO v1中是直接预测BBox的坐标,而不像Faster R-CNN和SSD那样,是预测Anchor的回归参数的!
- 在YOLO v1中是没有Anchor这个概念(直接预测BBox的坐标,而不是预测回归参数)
在
eval()时,对于每个目标的概率是通过条件类别概率乘上confidence参数的
对于每一个网格而言,它有 C C C类别,那么就会有 C C C个类别分数,即条件类别概率: Pr(Class i _i i | Object) —— 它是目标前提下的概率。而confidence就是Pr(Object) * IoU pred truth ^{\text{truth}}_{\text{pred}} predtruth。Pr(Class i _i i | Object) * Pr(Object)就可以得到Pr(Class i _i i),公式如下:
每 个 目 标 的 概 率 = P r ( C l a s s i ∣ O b j e c t ) × P r ( O b j e c t ) × I o U p r e d t r u t h = P r ( C l a s s i ) × I o U p r e d t r u t h \begin{aligned} 每个目标的概率 & =\mathrm{Pr}(\mathrm{Class}_i | \mathrm{Object}) \times \mathrm{Pr(Object)} \times \mathrm{IoU^{truth}_{pred}}\\ & = \mathrm{Pr}(\mathrm{Class}_i) \times \mathrm{IoU^{truth}_{pred}} \end{aligned} 每个目标的概率=Pr(Classi∣Object)×Pr(Object)×IoUpredtruth=Pr(Classi)×IoUpredtruth
通过这个表达式我们可以知道:
- 它为某个目标的概率
- 预测的BBox和GTBBox的重合程度(IoU)
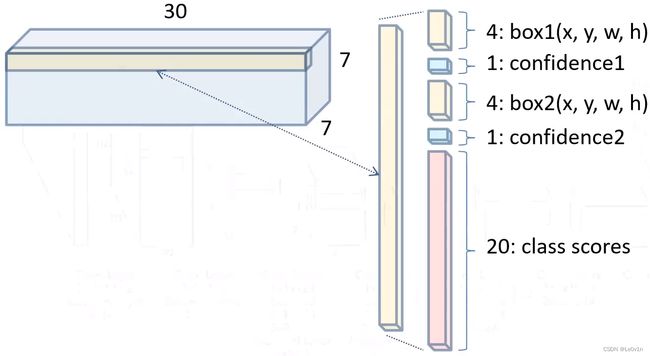
一个网格需生成两个BBox,每个BBox除了要预测4个坐标外,还需要预测一个confidence(置信度),即
参数 grid cell = [ ( x , y , h , w ) + c 第 一 个 BBox ] + [ ( x , y , h , w ) + c 第 二 个 BBox ] + [ 所 有 类 别 的 分 数 ] = [ 4 + 1 第 一 个 BBox ] + [ 4 + 1 第 二 个 BBox ] + [ 20 ] = 5 第 一 个 BBox + 5 第 二 个 BBox + 20 = 30 \begin{aligned} \text{参数}_{\text{grid cell}} & = [\underset{第一个\text{BBox}}{(x, y, h, w) + c}] + [\underset{第二个\text{BBox}}{(x, y, h, w) + c}] + [所有类别的分数]\\ & = [\underset{第一个\text{BBox}}{4 + 1}] + [\underset{第二个\text{BBox}}{4 + 1}] + [20] \\ & = \underset{第一个\text{BBox}}{5} + \underset{第二个\text{BBox}}{5} + 20 \\ & = 30 \end{aligned} 参数grid cell=[第一个BBox(x,y,h,w)+c]+[第二个BBox(x,y,h,w)+c]+[所有类别的分数]=[第一个BBox4+1]+[第二个BBox4+1]+[20]=第一个BBox5+第二个BBox5+20=30
1.4 网络结构
如果没有标
s,那么它默认的stride=1
Q1: fc(1470)中的1470是怎么来的?
A1:因为输出是[7, 7, 30],而这个输出特征图是经过reshape得到的,所以经过FC之后,输出的一维向量shape应该为1470。
Q2:为什么是[7, 7, 30]?
A2:7×7代表将图片划分为7×7个网格,30为每个网格的信息(参数个数)。
1.5 损失函数
在计算这些损失时,主要使用的是误差平方和这个函数进行的
误差平方和:
误 差 = ( 预 测 的 x − 真 实 的 x ) 2 + ( 预 测 的 y − 真 实 的 y ) 2 = ( 误 差 1 ) 2 + ( 误 差 2 ) 2 \begin{aligned} 误差 & = (预测的x - 真实的x)^2 + (预测的y - 真实的y)^2 \\ & = (误差1)^2 + (误差2)^2 \end{aligned} 误差=(预测的x−真实的x)2+(预测的y−真实的y)2=(误差1)2+(误差2)2
这就是误差平方和
1.5.1 BBox损失
其中:
- x i , y i , w i , h i x_i, y_i, w_i, h_i xi,yi,wi,hi为预测值
- x i ^ , y i ^ , w i ^ , h i ^ \hat{x_i}, \hat{y_i}, \hat{w_i}, \hat{h_i} xi^,yi^,wi^,hi^为GT值
- 1 \mathbb{1} 1
对于 w w w和 h h h的损失,加 \sqrt{} 的目的是放大[小目标]的损失(不同大小的目标,偏移相同的距离得到损失是不一样的)
如果使用 y = x y=x y=x这样的策略,那么在相同偏移量的情况下,二者的loss是相同的。看右面的图,很明显,对于小目标而言它位移相对更大,理应有更大的损失。
为了达到这样的效果,作者使用了开根号,对于 y = x y=\sqrt{x} y=x来说, x x x越大, y y y越平缓。
1.5.2 confidence损失
其中:
- 1 i j obj \mathbb{1}^{\text{obj}}_{ij} 1ijobj表示当前为目标时为1,不为目标时为0 —— 正样本为1,负样本为0
- 1 i j noobj \mathbb{1}^{\text{noobj}}_{ij} 1ijnoobj表示当前不为目标时为1,是目标时为0 —— 负样本为1,正样本为0
- λ noobj \lambda_{\text{noobj}} λnoobj表示不为目标时的一个系数 —— 负样本置信度误差的权重
因为之前就说过了,这里的confidence置信度指的是当前预测的BBox和GTBox的IoU值,即该预测BBox为张样本的概率。而不是当前BBox的类别概率。
Confidence = Pr(Object) * IoU pred truth ^{\text{truth}}_{\text{pred}} predtruth
对于正样本,它的真实值 C i ^ \hat{C_i} Ci^为1;对于负样本,它的真实值 C i ^ \hat{C_i} Ci^应该为0。
1.5.3 类别损失
- p i ( c ) p_i(c) pi(c)为该grid cell的类别预测值为 c c c类别的概率
- p i ^ ( c ) \hat{p_i}(c) pi^(c)为该grid cell对应的GTBox的 c c c类别的概率(二值化,只能是0或1)
1.6 YOLO v1存在的问题
- 对密集目标检测效果很差 —— 比如有一群鸟 —— 原因是grid cell数量少且每个grid cell只预测两个BBox —— 最多预测7×7×2=98个目标
- 当目标出现新的尺寸或配置时,检测效果也很差
- 主要错误的原因是定位错误 —— 主要因为v1是直接预测目标坐标而不像Faster R-CNN和SSD那样预测回归参数 —— 基于此,从YOLO v2开始,使用基于Anchor的回归预测机制。
1.7 YOLO v1中的Bounding Box 和 Anchor 有什么区别?
Bounding Box(BBox)译为边界框,在YOLO v1中它的中心位于所属的grid cell中心,它进行定位回归时,不是用回归参数一点一点去进行调整,而是直接预测目标的图像坐标,这就导致YOLO v1 BBox的定位回归很差 —— 野蛮生长。
Anchor译为锚框,像Faster R-CNN和SSD那样,先生成Anchor,然后在定位回归时预测的是回归参数,即anchor的移动参数。不是直接让anchor预测目标的位置,所以定位效果比YOLO v1要好 —— 微调。
2. YOLO v2
论文题目:YOLO9000: Better, Faster, Stronger
论文地址:https://arxiv.org/abs/1612.08242
2.1 YOLO v2 与其他网络的性能对比
2.2 YOLO v2相比v1的尝试
- Batch Normalization
- High Resolution Classifier
- Convolutional With Anchor Boxes
- Dimension Clusters
- Direct Location Prediction
- Fine-Grained Features
- Multi-scale Training
2.2.1 Batch Normalization
在YOLO v1时没有使用BN层,在v2中每个卷积层后面加上了BN层。好处:
- 加速模型收敛
- 减少所需使用使用的正则化操作 —— BN对模型起到了正则化作用
- 提升2%的mAP
- 作者提出一个观点:使用了BN层就可以不用Dropout层
2.2.2 High Resolution Classifier,高分辨率分类器

在YOLO v1中训练backbone的输入像素为224×224(主要是那个时候训练backbone基本上都是用224×224的图片),然而在YOLO v2中作者使用了一个更大输入尺寸 —— 448×448。即网络先用224×224的图片进行训练,训练完毕后再对其进行10个Epoch的微调(迁移学习),此时输入图片大小为448×448。
采用更大输入图片的分类器给目标检测网络带来哪些好处呢?
- 4%mAP
2.2.3 Convolutional With Anchor Boxes,基于Anchor Boxes的卷积
Convolutional With Anchor Boxes,基于Anchor Boxes的卷积,说白了就是基于Anchor的目标边界框预测(不像v1中那样野蛮生长了)。
YOLO predicts the coordinates of bounding boxes directly using fully connected layers on top of the convolutional feature extractor.Instead of predicting coordinates directly Faster R-CNN predicts bounding boxes using hand-picked priors. Using only convolutional layers the region proposal network (RPN) in Faster R-CNN predicts offsets and confidences for anchor boxes. Since the prediction layer is convolutional, the RPN predicts these offsets at every location in a feature map. Predicting offsets instead of coordinates simplifies the problem and makes it easier for the network to learn.
YOLO v1直接使用卷积特征提取器顶部的全连接层直接预测边界框的坐标。Faster R-CNN 使用手工挑选的先验预测边界框,而不是直接预测坐标。 Faster R-CNN 中的区域提议网络 (RPN) 仅使用卷积层来预测锚框的偏移量和置信度。 由于预测层是卷积层,因此 RPN 会在特征图中的每个位置预测这些偏移量。 预测偏移量而不是坐标可以简化问题并使网络更容易学习。
Faster R-CNN 使用手工挑选的先验预测边界框:Faster R-CNN先挑选了集中尺寸的预测框,然后对于每个预测特征图上的每个像素都会进行anchor的生成,即每个像素上都会生成这些先验的预测框,之后通过RPN网络预测其回归的参数和置信度(这里的置信度是该Anchor的类别概率,和YOLO v1中的confidence不同)。
这里作者对Faster R-CNN中坐标回归表示肯定
We remove the fully connected layers from YOLO and use anchor boxes to predict bounding boxes. First we eliminate one pooling layer to make the output of the network’s convolutional layers higher resolution. We also shrink the network to operate on 416 input images instead of 448×448. We do this because we want an odd number of locations in our feature map so there is a single center cell. Objects, especially large objects, tend to occupy the center of the image so it’s good to have a single location right at the center to predict these objects instead of four locations that are all nearby. YOLO’s convolutional layers downsample the image by a factor of 32 so by using an input image of 416 we get an output feature map of 13 × 13.
我们从 YOLO 中移除全连接层,并使用锚框来预测边界框。 首先,我们消除了一个池化层,以使网络卷积层的输出具有更高的分辨率。 我们还缩小了网络以对 416 个输入图像而不是 448×448 进行操作。 我们这样做是因为我们想要在我们的特征图中有奇数个位置,所以只有一个中心单元。 目标,尤其是大目标,往往占据图像的中心,因此最好在中心有一个位置来预测这些物体,而不是四个都在附近的位置。 YOLO 的卷积层将图像下采样 32 倍,因此通过使用 416 的输入图像,我们得到 13 × 13 的输出特征图。
这里说明了YOLO的architecture改动
When we move to anchor boxes we also decouple the class prediction mechanism from the spatial location and instead predict class and objectness for every anchor box. Following YOLO, the objectness prediction still predicts the IOU of the ground truth and the proposed box and the class predictions predict the conditional probability of that class given that there is an object.
当我们移动到锚盒时,我们还将类预测机制与空间位置解耦,而是为每个锚盒预测类和对象。 在 YOLO 之后,objectness prediction 仍然预测 ground truth 和提出的 box 的 IOU,并且类预测在给定对象的情况下预测该类的条件概率。
Using anchor boxes we get a small decrease in accuracy. YOLO only predicts 98 boxes per image but with anchor boxes our model predicts more than a thousand. Without anchor boxes our intermediate model gets 69.5 mAP with a recall of 81%. With anchor boxes our model gets 69.2 mAP with a recall of 88%. Even though the mAP decreases, the increase in recall means that our model has more room to improve.
使用锚框,我们的准确性会略有下降。 YOLO v1仅预测每张图像 98 个框,但使用锚框,我们的模型预测超过 1000 个框。
- 在没有锚框的情况下,我们的中间模型得到 69.5 mAP,召回率为 81%
- 使用锚框,我们的模型获得 69.2 mAP,召回率为 88%
尽管 mAP 降低了,但召回率的增加意味着我们的模型还有更多的改进空间。
2.2.4 Dimension Clusters,维度聚类 —— anchor先验框的聚类
We encounter two issues with anchor boxes when using them with YOLO. The first is that the box dimensions are hand picked. The network can learn to adjust the boxes appropriately but if we pick better priors for the network to start with we can make it easier for the network to learn to predict good detections. Instead of choosing priors by hand, we run k-means clustering on the training set bounding boxes to automatically find good priors. If we use standard k-means with Euclidean distance larger boxes generate more error than smaller boxes. However, what we really want are priors that lead to good IOU scores, which is independent of the size of the box. Thus for our distance metric we use:
在将锚框与 YOLO 一起使用时,我们遇到了两个问题。 首先是anchor尺寸是手工挑选的。 网络可以学习适当地调整框,但是如果我们为网络选择更好的先验,我们可以使网络更容易学习预测良好的检测。 我们不是手动选择先验,而是在训练集边界框上运行 k-means 聚类以自动找到好的先验。 如果我们使用具有欧几里德距离的标准 k-means,则较大的框会比较小的框产生更多的错误。 然而,我们真正想要的是导致良好 IOU 分数的先验,这与框的大小无关。 因此,对于我们的距离度量,我们使用:
d ( box, centroid ) = 1 − IoU(box, centroid) d(\text{box, centroid}) = 1 - \text{IoU(box, centroid)} d(box, centroid)=1−IoU(box, centroid)
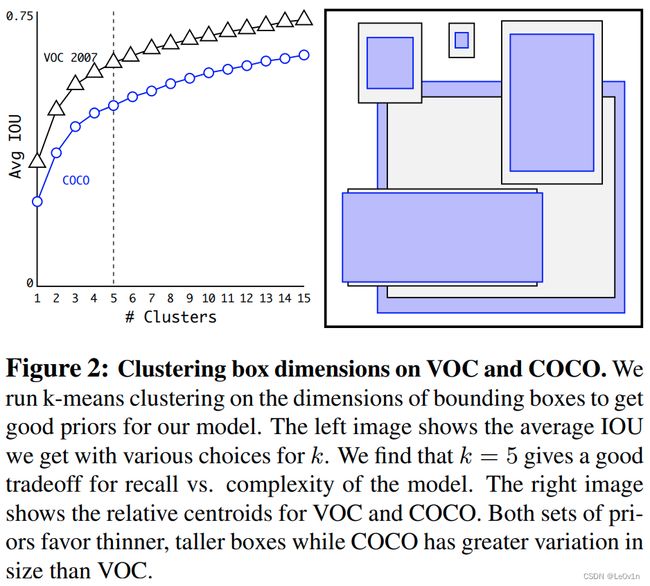
We run k-means for various values of k and plot the average IOU with closest centroid, see Figure 2. We choose k = 5 as a good tradeoff between model complexity and high recall. The cluster centroids are significantly different than hand-picked anchor boxes. There are fewer short, wide boxes and more tall, thin boxes.
我们对不同的 k 值运行 k-means 并绘制具有最近质心的平均 IOU,见图 2。我们选择 k = 5 作为模型复杂性和高召回率之间的良好折衷。 聚类质心与手工挑选的锚框有很大不同。 短而宽的盒子更少,而高而薄的盒子更多。
矮胖的先验框比较少,高瘦的先验框比较多 —— 这取决于训练集Object的比例
We compare the average IOU to closest prior of our clustering strategy and the hand-picked anchor boxes in Table 1. At only 5 priors the centroids perform similarly to 9 anchor boxes with an average IOU of 61.0 compared to 60.9. If we use 9 centroids we see a much higher average IOU. This indicates that using k-means to generate our bounding box starts the model off with a better representation and makes the task easier to learn.
我们将平均 IOU 与我们的聚类策略的最接近先验和表 1 中手工挑选的锚框进行比较。在只有 5 个先验时,质心的性能与 9 个锚框相似,平均 IOU 为 61.0,而平均 IOU 为 60.9。 如果我们使用 9 个质心,我们会看到更高的平均 IOU。 这表明使用 k-means 生成我们的边界框以更好的表示启动模型并使任务更容易学习。
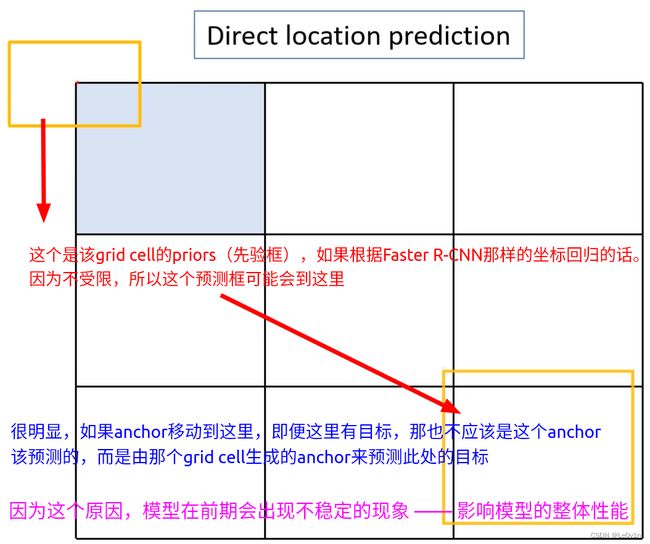
2.2.5 Direct Location Prediction,直接定位预测 —— 预测边界框定位回归
When using anchor boxes with YOLO we encounter a second issue: model instability, especially during early iterations. Most of the instability comes from predicting the ( x , y ) (x, y) (x,y) locations for the box. In region proposal networks the network predicts values t x t_x tx and t y t_y ty and the ( x , y ) (x, y) (x,y) center coordinates are calculated as:
在 YOLO 中使用锚框时,我们遇到了第二个问题:模型不稳定,尤其是在早期迭代期间。 大多数不稳定性来自于预测边界框的 ( x , y ) (x, y) (x,y) 位置。 在RPN网络中,网络预测值 t x t_x tx 和 t y t_y ty 以及 ( x , y ) (x, y) (x,y) 中心坐标计算如下:
x = ( t x × w a ) + w a y = ( t y × h a ) + y a \begin{aligned} & x = (t_x \times w_a) + w_a \\ & y = (t_y \times h_a) + y_a \end{aligned} x=(tx×wa)+way=(ty×ha)+ya
论文中给出的公式其实是错误的,不是
-而应该是+
其中:
- t x , t y t_x, t_y tx,ty为预测框的中心点回归参数
- x , y x, y x,y为预测框的中心点坐标
- x a , y a , w a , h a x_a, y_a, w_a, h_a xa,ya,wa,ha为anchor的中心点坐标和anchor宽度、高度。
For example, a prediction of t x = 1 t_x = 1 tx=1 would shift the box to the right by the width of the anchor box, a prediction of t x = − 1 t_x = −1 tx=−1 would shift it to the left by the same amount.
例如, t x = 1 t_x = 1 tx=1 的预测会将框向右移动锚框的宽度, t x = − 1 t_x = -1 tx=−1 的预测会将其向左移动相同的量。
This formulation is unconstrained so any anchor box can end up at any point in the image, regardless of what location predicted the box. With random initialization the model takes a long time to stabilize to predicting sensible offsets. Instead of predicting offsets we follow the approach of YOLO and predict location coordinates relative to the location of the grid cell. This bounds the ground truth to fall between 0 and 1. We use a logistic activation to constrain the network’s predictions to fall in this range.
由于这个公式是不受约束的,因此任何锚框都可以在图像中的任何点结束,而不管预测框的位置如何。 通过随机初始化,模型需要很长时间才能稳定到预测合理的偏移量。 我们遵循 YOLO 的方法并预测相对于网格单元位置的位置坐标,而不是预测偏移量。 这将基本事实限制在 0 和 1 之间。我们使用逻辑激活来限制网络的预测落在这个范围内。
由于上面那个公式中的预测值 t x , t y t_x, t_y tx,ty没有限制,所以这种回归方式的预测框可能出现在图像中的任意一个地方,举个极端的例子:
为了改善这种情况,v2中采用了另外一种方法。
The network predicts 5 bounding boxes at each cell in the output feature map. The network predicts 5 5 5 coordinates for each bounding box, t x t_x tx, t y t_y ty, t w t_w tw, t h t_h th, and t o t_o to. If the cell is offset from the top left corner of the image by ( c x , c y ) (c_x, c_y) (cx,cy) and the bounding box prior has width and height p w p_w pw, p h p_h ph, then the predictions correspond to:
网络预测输出特征图中每个单元格的 5 个边界框。 网络为每个边界框 t x t_x tx、 t y t_y ty、 t w t_w tw、 t h t_h th 和 t o t_o to 预测 5 5 5 坐标。 如果单元格从图像的左上角偏移 ( c x , c y ) (c_x, c_y) (cx,cy) 并且边界框先验具有宽度和高度 p w p_w pw, p h p_h ph,则预测对应于:
假设将priors设置在每一个grid cell的左上角,它的中心点坐标为 c x , c y c_x, c_y cx,cy,宽度和高度为 p w , p h p_w, p_h pw,ph,则回归后的anchor坐标为:
b x = σ ( t x ) + c x b y = σ ( t y ) + c y b w = p w e t w b h = p h e t h Pr(object) × IoU ( b , object ) = σ ( t o ) \begin{aligned} b_x & = \sigma(t_x) + c_x \\ b_y & = \sigma(t_y) + c_y \\ b_w & = p_we^{t_w} \\ b_h & = p_he^{t_h} \\ \text{Pr(object)} \times \text{IoU}(b, \text{object}) & = \sigma(t_o) \end{aligned} bxbybwbhPr(object)×IoU(b,object)=σ(tx)+cx=σ(ty)+cy=pwetw=pheth=σ(to)
其中:
- t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th为预测的关于anchor的偏移量
- σ ( ⋅ ) \sigma(\cdot) σ(⋅)为Sigmoid函数 —— 将输入映射到 [ 0 , 1 ] [0, 1] [0,1]
- p w , p h p_w, p_h pw,ph为先验框的宽度和高度
- t o t_o to为v1中的confidence,即anchors与GTBox的IoU值,同样被 σ \sigma σ函数所限制
与Faster R-CNN的公式相比, σ ( t x ) \sigma(t_x) σ(tx)和$\sigma(t_y) 对预测值进行了限制(将其限制在[0, 1])—— 回归后anchors的中心坐标不会跑出它的grid cell(因为偏移量是相对anchor的左上角而言的,所以绝对跑不出去!),例子如下:
这样就实现了 目标中心点落在某个grid cell区域内的目标被其grid cell产生的anchors(priors)预测,中心点没有落在该grid cell中,那么就不由该grid cell去负责预测了。—— 解决了anchor会出现在图像中的任意地方。
Since we constrain the location prediction the parametrization is easier to learn, making the network more stable. Using dimension clusters along with directly predicting the bounding box center location improves YOLO by almost 5% over the version with anchor boxes.
由于我们限制了位置预测,参数化更容易学习,使网络更稳定。 使用维度聚类以及直接预测边界框中心位置,与使用锚框的版本相比,YOLO 提高了近 5%。
好处:
- 相比使用Faster R-CNN那样的坐标回归,使用①维度聚类得到priors和②限制预测位置的方法,mAP提高了5%。
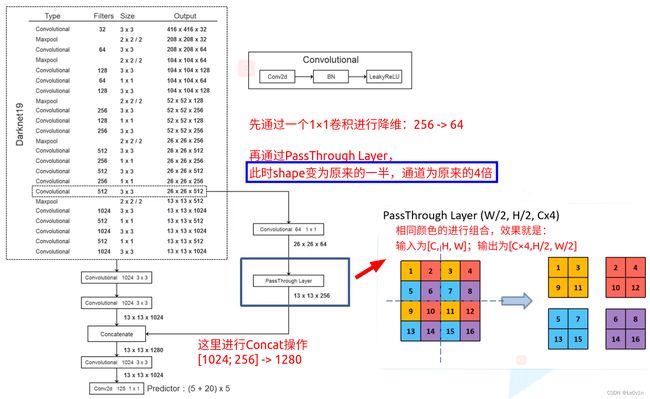
2.2.6 Fine-Grained Features,细粒度特征
This modified YOLO predicts detections on a 13 × 13 feature map. While this is sufficient for large objects, it may benefit from finer grained features for localizing smaller objects. Faster R-CNN and SSD both run their proposal networks at various feature maps in the network to get a range of resolutions. We take a different approach, simply adding a passthrough layer that brings features from an earlier layer at 26 × 26 resolution.
这个修改后的 YOLO 预测 13 × 13 特征图上的检测。 虽然这对于大型物体来说已经足够了,但它可能会受益于用于定位较小物体的更细粒度的特征。 Faster R-CNN 和 SSD 都在网络中的各种特征图上运行他们的proposal网络,以获得一系列分辨率。 我们采用不同的方法,只需添加一个直通层,以 26 × 26 的分辨率从较早的层引入特征。
深层的特征图因为感受野大,所以对于检测大目标是比较合适的。但对于小目标来说,太大的感受野并不是一件好事。为了解决这个问题,作者加入了一个直通层(passthrough layer)来融合相对没那么深的特征图,以此来加强小目标的检测效果。
13×13的特征图融合26×26的特征图
The passthrough layer concatenates the higher resolution features with the low resolution features by stacking adjacent features into different channels instead of spatial locations, similar to the identity mappings in ResNet. This turns the 26 × 26 × 512 feature map into a 13 × 13 × 2048 feature map, which can be concatenated with the original features. Our detector runs on top of this expanded feature map so that it has access to fine grained features. This gives a modest 1% performance increase.
直通层通过将相邻特征堆叠到不同的通道而不是空间位置来连接更高分辨率的特征和低分辨率的特征,类似于 ResNet 中的恒等映射。 这将 26 × 26 × 512 的特征图变成了 13 × 13 × 2048 的特征图,可以与原始特征进行拼接。 我们的检测器在这个扩展的特征图之上运行,因此它可以访问细粒度的特征。 这会带来 1% 的适度性能提升。
这里的2048是没有使用1×1卷积降维的情况
但在源码中,作者使用了1×1卷积进行了降维
2.2.7 Multi-scale Training,多尺度训练
The original YOLO uses an input resolution of 448 × 448. With the addition of anchor boxes we changed the resolution to 416×416. However, since our model only uses convolutional and pooling layers it can be resized on the fly. We want YOLOv2 to be robust to running on images of different sizes so we train this into the model.
原始 YOLO 使用 448 × 448 的输入分辨率。通过添加锚框,我们将分辨率更改为 416×416。 然而,由于我们的模型只使用卷积层和池化层,它可以动态调整大小。 我们希望 YOLOv2 能够在不同大小的图像上运行,因此我们将其训练到模型中。
416×416是因为想要得到奇数个grid cell,这样它们的中心点就是一个像素而不是比0.5个像素,经过下采样后,最终的预测特征图大小为13×13,它是奇数的,所以有很明显的中心点。
Instead of fixing the input image size we change the network every few iterations. Every 10 batches our network randomly chooses a new image dimension size. Since our model downsamples by a factor of 32, we pull from the following multiples of 32: {320, 352, …, 608}. Thus the smallest option is 320 × 320 and the largest is 608 × 608. We resize the network to that dimension and continue training.
我们不是固定输入图像的大小,而是每隔几次迭代就改变网络。 每 10 批我们的网络随机选择一个新的图像尺寸。 由于我们的模型下采样了 32 倍,我们从以下 32 的倍数中提取:{320, 352, …, 608}。 因此,最小的选项是 320 × 320,最大的选项是 608 × 608。我们将网络调整到该维度并继续训练。
这里所说的batches指的是Epoch
{320, 352, …, 608} = {32×10, 32×11, …, 32×19}
This regime forces the network to learn to predict well across a variety of input dimensions. This means the same network can predict detections at different resolutions. The network runs faster at smaller sizes so YOLOv2 offers an easy tradeoff between speed and accuracy.
这种制度迫使网络学会在各种输入维度上进行良好的预测。 这意味着同一个网络可以预测不同分辨率的检测。 网络在较小的尺寸下运行得更快,因此 YOLOv2 在速度和准确性之间提供了一个简单的权衡。
At low resolutions YOLOv2 operates as a cheap, fairly accurate detector. At 288 × 288 it runs at more than 90 FPS with mAP almost as good as Fast R-CNN. This makes it ideal for smaller GPUs, high framerate video, or multiple video streams.
在低分辨率下,YOLOv2 是一种廉价且相当准确的检测器。 在 288 × 288 时,它以超过 90 FPS 的速度运行,mAP 几乎与 Fast R-CNN 一样好。 这使其非常适合较小的 GPU、高帧率视频或多个视频流。
At high resolution YOLOv2 is a state-of-the-art detector with 78.6 mAP on VOC 2007 while still operating above real-time speeds. See Table 3 for a comparison of YOLOv2 with other frameworks on VOC 2007 (Figure 4).
在高分辨率下,YOLOv2 是最先进的检测器,在 VOC 2007 上具有 78.6 mAP,同时仍以高于实时速度运行。 有关 YOLOv2 与其他框架在 VOC 2007 上的比较,请参见表 3(图 4)。
Note:
- 这里采用多尺度训练并不是训练backbone,而是训练网络定位和分类回归!
- 训练backbone用的448×448的输入图片!
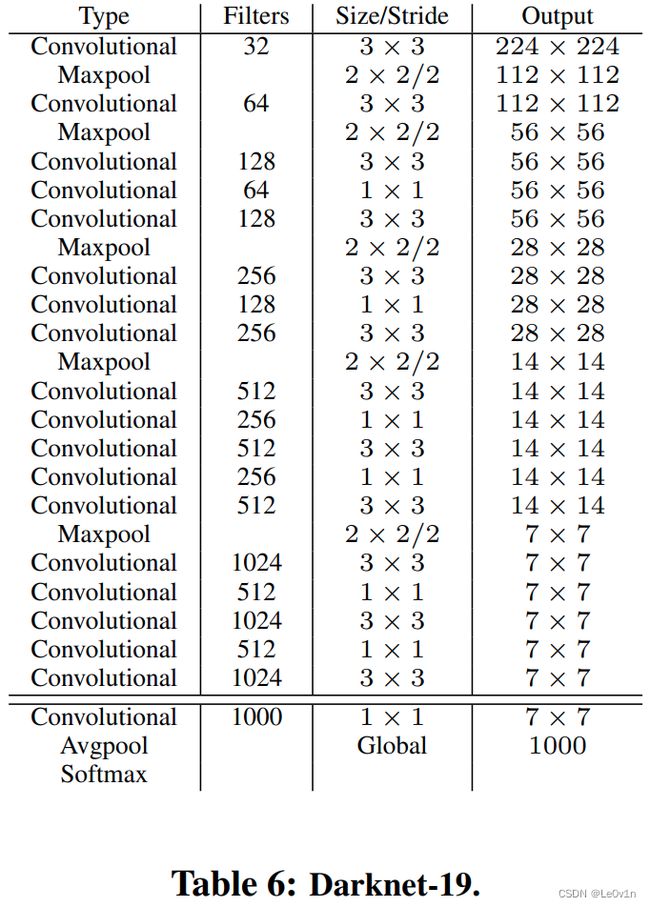
2.3 YOLO v2的backbone —— Darknet-19
- 19代表卷积层的个数
Darknet-19(224×224)only requires 5.58 billion operations to process an image yet achieves 72.9% top-1 accuracy and 91.2% top-5 accuracy on ImageNet.
Darknet-19 (224×224)只需要 55.8 亿次操作来处理图像,但在 ImageNet 上实现了 72.9% 的 top-1 准确率和 91.2% 的 top-5 准确率。
虽然YOLO v2的backbone在训练时使用的输入图片大小为448×448,但这里为了展示Darknet-19的性能,将其输入设置为了224×224,因为其他的分类网络一般的输入均为224×224。
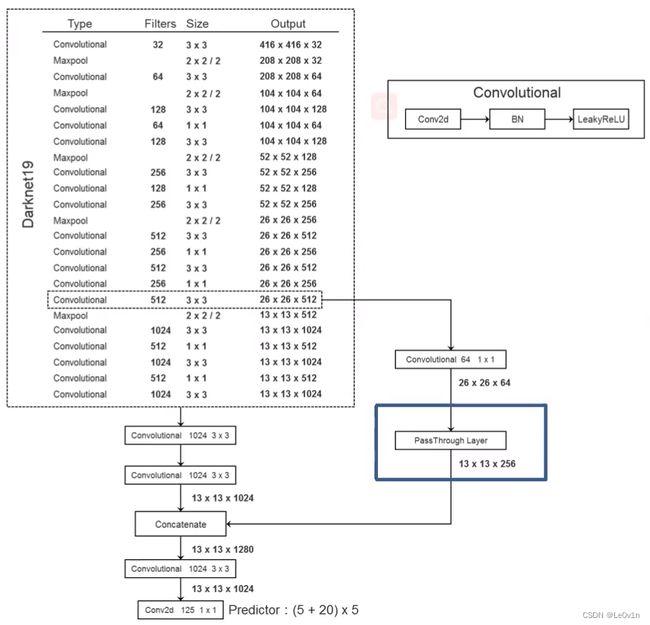
2.4 YOLO v2的整体框架
- Filters代表卷积核的个数(也就是输出的通道数)
- Size为卷积核大小
- 默认stride=1
- 加了
/,后面的数表示stride
- 每一个Convolutional都包含三个部分
- Conv2d(不包含bias —— 因为有了BN)
- BN
- LeakyReLU(也就是PReLU)
- 最后的
Conv2d 125 1×1就只是一个1×1卷积,没有BN和激活函数
作者将自己提出的分类网络Darknet-19用到了YOLO v2这个目标检测网络中并修改了其部分结构:

- 移除了最后一层卷积和其之后的层结构
- 在后面添加三个3×3的卷积层(每个卷积层的卷积核个数为1024)
- 在添加的3个卷积层中,第二个卷积层之后增加PassThrough层(直通层)
- 最后接上一个1×1端卷积层,其输出个数为所需检测的目标参数(这里为(5+20)×5)
所需检测的目标参数:
对于VOC数据集,网络会预测5个Anchor,每个Anchor有5个参数(x, y, w, h, confidence),其中(x, y, w, h)为anchor的回归信息;confidence为该anchor与GTBox的IoU值。VOC数据集有20个类别,所以对于每一个Anchor均需预测20个类别分数。
故需要(5 + 20) * 5 = 125个需要预测的参数
与YOLO v1不同,YOLO v1是grid cell预测类别分数,而v2是每一个anchor均需要预测20个分数。
2.5 YOLO v2训练细节
2.5.1 论文中没有提及
- 如何匹配正负样本
- 如何计算误差
这两部分会在YOLO v3中进行细讲
2.5.2 论文提及的训练细节
- 在优化器中使用了权重衰减和动量
- 使用了与YOLO v1相同的数据增强处理以及SSD中采用的随机裁剪和颜色偏移的增强方式
- 在COCO和VOC上的训练策略是相同
3. YOLO v3
论文题目:YOLOv3: An Incremental Improvement
论文地址:https://arxiv.org/abs/1804.02767

2018年发表在CVPR,其论文中的内容比较少 —— 没有太多的创新点,基本上就是整合了当时比较主流网络的优点。
3.1 YOLO v3与其他网络的对比
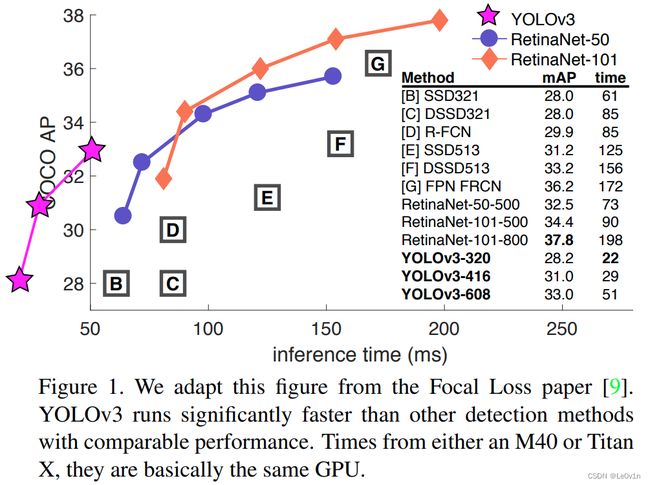
数据集为MS COCO数据,相比于其他网络而言,YOLO v3的速度是非常快的,但其AP并不是很高。
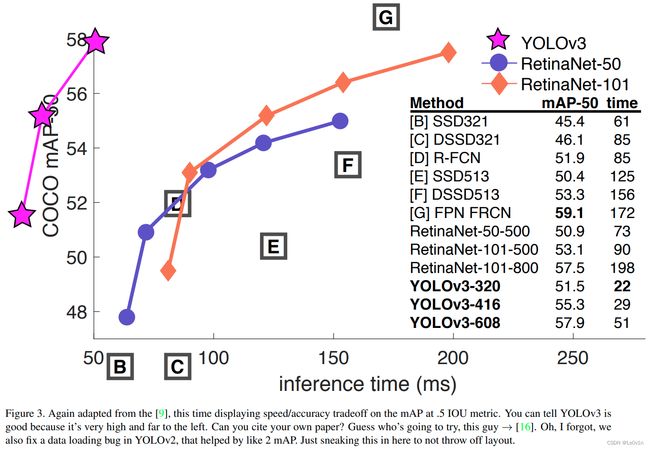
该图的纵坐标为COCO APIoU=0.5 —— PASCAL VOC的mAP。通过该指标来看,YOLO v3的速度和准确率都比较高。
3.2 YOLO v3网络架构
3.2.1 backbone —— Darknet-53
修改了backbone —— Darknet-19 -> Darknet-53
根据右上角的表格我们可以知道,Darknet-19变为Darknet-53提升了分类的准确率(和ResNet-152持平),但其FPS腰斩。
虽然速度降低了,但重点不是在这里。而是Darknet-53准确率和ResNet-152持平,但速度是其2倍! —— Darknet-53也是非常强劲的分类网络
53表示卷积层有53个,注意最后分类层中全连接层被卷积层替代,所以有53个卷积层。
Q:为什么Darknet-53的效果比ResNet-152的效果要好?
A:Darknet-53没有MaxPooling层(所有下采样都是通过卷积层实现的)
Q:为什么Darknet-53的速度比ResNet-152要快?
A:ResNet-152的卷积核个数比Darknet-53要多很多 —— Darknet-53的参数要少,运算量少 -> 速度快
3.2.2 整体框架
- Predict one: 13×13 -> 预测大目标
- Predict one: 26×26 -> 预测中目标
- Predict one: 52×52 -> 预测小目标
3.3 目标检测框的预测机制
v3采用了和v2一样的机制。
- t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th为预测的关于anchor的偏移量
- σ ( ⋅ ) \sigma(\cdot) σ(⋅)为Sigmoid函数 —— 将输入映射到 [ 0 , 1 ] [0, 1] [0,1]
- p w , p h p_w, p_h pw,ph为先验框的宽度和高度
- b x , b y , b w , b h b_x, b_y, b_w, b_h bx,by,bw,bh为最终边界框的中心点坐标以及宽度、高度
- c x , c y c_x, c_y cx,cy当前grid cell左上角点的坐标
- 虚线的矩形框对应的是priors(anchor) —— 这里我们只需关心其宽度和高度这个参数即可
- 图中蓝色矩形框是网络预测的最终目标位置以及大小
Sigmoid函数的存在使得预测值不会超过当前的grid cell —— 和v2是一样的
通过图中的公式就可以将网络预测的回归参数转化为最终的目标边界框具体坐标。
3.4 grid cell的priors的比例
针对每一个预测特征图而言,每一个先验框均有3种比例(3种不同的anchor模板)。

因为YOLO v3有3种不同尺寸的预测特征图,所以将不同尺寸的anchor分配给不同的预测特征图,具体细节如下表所示。
感受野越大,预测的目标尺寸应该越大
反之亦然
3.5 正负样本的匹配
- 如果边界框先验与GTBox的重叠比任何其他边界框先验多,则该值应为 1。
- 如果边界框先验不是最好的,但确实与GTBox重叠超过某个阈值,我们将忽略预测,遵循 [17]。
我们使用 0.5 的阈值。 与 [17] 不同,我们的系统只为每个GTBox分配一个边界框先验。 如果未将边界框先验分配给GTBox,则不会对坐标或类别预测造成损失,只会对对象性造成损失。
[17]为Faster R-CNN
针对每一个GT而言都会分配一个正样本 —— 一张图片中有几个GT目标就有几个正样本。
分配原则:
- 先验框与GTBox的IoU最大的作为正样本
- 如果其他先验框与该GTBox的IoU的值不是最大,但IoU超过了设置的阈值(0.5) -> 直接丢弃这个先验框,即这个先验框既不是正样本也不是负样本,而是直接弃用
- 剩下与GTBox的IoU不是最大且小于设定阈值的先验框均设置为负样本
- 如果先验框没有分配给某一个GTBox(即当前的先验框不是正样本的话),那么它既没有定位损失,也没有类别损失,仅仅只有confidence损失(与GTBox的IoU损失)
3.6 YOLO v3源码的正负样本匹配策略
如果我们按上论文中(也就是上面的这种)正负样本匹配策略的话,会发现正样本的数量太少了 —— 导致网络很难训练。
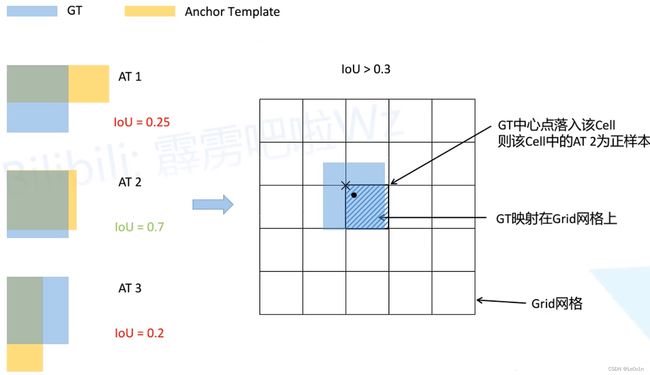
针对每一个预测特征图而言,每一个先验框均有3种比例(3种不同的anchor模板),如下所示:

- 将每一个Anchor模板与GTBox进行IoU的计算(将二者的左上角重合后再计算IoU)
- 设置IoU阈值(0.3),只要Anchor与GTBox的IoU > 0.3,该Anchor都会被设置为正样本 —— 只有第二个anchor模板符合条件,为正样本
- 将GTBox映射到预测特征图上(其中黑色的圆点为GTBox的中心点,×为GTBox所属grid cell的左上角坐标)
- GTBox中心点落在哪个grid cell,哪个grid cell对应的anchor模板2就为正样本
Q:如果这三个anchor模板与GTBox的IoU均大于阈值呢?
A:如果出现这种情况,那么GTBox所属的grid cell的3个anchor模板均为正样本
这种策略中,只要Anchor与GTBox的IoU大于阈值,那么它就是正样本,小于阈值就是负样本(没有论文策略中废弃Anchor的做法了) —— 目的就是为了扩充正样本的数量。
这种策略在实践中的效果确实比论文中的策略要好一些
3.7 损失函数
YOLO v3整体损失计算如下:
L ( o , c , O , C , l , g ) = λ 1 L conf ( o , c ) 置 信 度 损 失 + λ 2 L cls ( O , C ) 分 类 损 失 + λ 3 L loc ( l , g ) 定 位 损 失 L(o, c, O, C, l, g) = \lambda_1 \underset{置信度损失}{L_{\text{conf}}(o, c)} + \lambda_2 \underset{分类损失}{L_{\text{cls}}(O, C)} + \lambda_3 \underset{定位损失}{L_{\text{loc}}(l, g)} L(o,c,O,C,l,g)=λ1置信度损失Lconf(o,c)+λ2分类损失Lcls(O,C)+λ3定位损失Lloc(l,g)
其中 λ 1 , λ 2 , λ 3 \lambda_1, \lambda_2, \lambda_3 λ1,λ2,λ3为平衡系数。
3.7.1 置信度损失(Confidence Loss)
L conf ( o , c ) = − 1 N ∑ i ( o i ln ( c ^ i ) + ( 1 − o i ) ln ( 1 − c ^ i ) ) L_{\text{conf}}(o, c) = - \frac{1}{N} \sum_i (o_i \ln(\hat{c}_i) + (1-o_i) \ln(1-\hat{c}_i)) Lconf(o,c)=−N1i∑(oiln(c^i)+(1−oi)ln(1−c^i))
c ^ i = Sigmoid ( c i ) \hat{c}_i = \text{Sigmoid}(c_i) c^i=Sigmoid(ci)
其中,
- o i ∈ [ 0 , 1 ] o_i\in [0, 1] oi∈[0,1]表示预测目标边界框与GTBox的IoU
- c i c_i ci为预测值
- c ^ i \hat c_i c^i为 c i c_i ci通过Sigmoid函数得到的预测置信度
- N N N为正负样本总数。
论文中说使用的是逻辑回归,而逻辑回归一般都是BCE损失(即二值交叉熵损失)
Q:预测目标边界框是Anchor priors吗?
A:并不是,看下图。
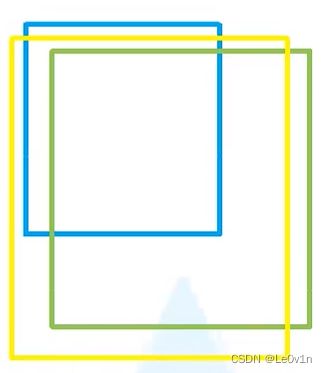
其中
- 蓝色框为Anchor priors
- 绿色框为GTBox
- 黄色框为预测目标边界框
预测目标边界框是Anchor根据预测值回归得到的,即 o i o_i oi是黄色框与绿色框的IoU值。
3.7.2 分类/类别损失(Classes Loss)
L cls ( O , C ) = − 1 N pos ∑ i ∈ pos ∑ j ∈ cls ( O i j ln ( C ^ i j ) + ( 1 − O i j ) ln ( 1 − C ^ i j ) ) L_{\text{cls}}(O, C) = - \frac{1}{N_{\text{pos}}} \sum_{i\in \text{pos}}\sum_{j\in \text{cls}}(O_{ij} \ln(\hat C_{ij}) + (1-O_{ij})\ln(1-\hat C_{ij})) \\ Lcls(O,C)=−Npos1i∈pos∑j∈cls∑(Oijln(C^ij)+(1−Oij)ln(1−C^ij))
C ^ i j = Sigmoid ( C i j ) \hat C_{ij} = \text{Sigmoid}(C_{ij}) C^ij=Sigmoid(Cij)
O i j = { 1 , 第 i 个 预 测 边 界 框 中 存 在 第 j 类 目 标 ; 0 , 第 i 个 预 测 边 界 框 中 不 存 在 第 j 类 目 标 . O_{ij}= \begin{cases} 1, & 第i个预测边界框中存在第j类目标; \\ 0, & 第i个预测边界框中不存在第j类目标. \\ \end{cases} Oij={1,0,第i个预测边界框中存在第j类目标;第i个预测边界框中不存在第j类目标.
其中:
- O i j ∈ { 0 , 1 } O_{ij}\in \{0, 1\} Oij∈{0,1}表示预测目标边界框 i i i中是否存在第 j j j类目标,是一个二值化函数,只能取0或1
- C ^ i j \hat C_{ij} C^ij为 C i j C_{ij} Cij通过Sigmoid函数得到的目标概率(即分类概率)
- N pos N_{\text{pos}} Npos为正样本的个数
这里的分类损失也是BCE损失。
例子:

我们需要检测图片中的[老虎,豹子,猫]这三个类别;左下角的图片中有两个类别,且均为猫。
- 目标1的GT概率为[0, 0, 1] —— one-hot编码
- 目标2的GT概率为[0, 0, 1] —— one-hot编码
假设网络的预测概率为:经过Sigmoid函数处理后得到的
- 目标1的预测概率为[0.1, 0.8, 0.9]
- 目标2的预测概率为[0.2, 0.7, 0.8]
我们发现,预测每个目标预测值的和并不是等于1的,之前我们使用Softmax交叉熵的时候,预测概率之和为1;而这里用的是BCE交叉熵,每一个输出值是直接通过Sigmoid函数进行处理的,每个预测值之间是互不干扰、相互独立的,所以就可能会出现 —— 该目标既有可能是豹子也有可能是猫的情况(就是可能出现多个概率较大的类别)。
验证:验证类别损失的BCE是否正确
import torch
import numpy as np
"""
reduction="none"表示求出BCELoss后不进行任何处理
如果不设置,默认是对其进行求均值处理 -> 返回一个均值
"""
loss = torch.nn.BCELoss(reduction="none")
# loss = torch.nn.BCELoss() # 0.5784000158309937
predicted_cls = [[0.1, 0.8, 0.9], [0.2, 0.7, 0.8]]
predict_cls_tensor = torch.tensor(predicted_cls, requires_grad=True)
gt_cls = [[0., 0., 1.], [0., 0., 1.]]
gt_cls_tensor = torch.tensor(gt_cls)
loss_res = loss(input=predict_cls_tensor, target=gt_cls_tensor)
print(f"PyTorch官方实现的结果: {np.round(loss_res.detach().numpy(), decimals=5)}") # decimals: 将数组四舍五入到给定的小数位数。
def bce(c, o):
# 这里的np.log就是ln(以e为底)
return np.round(-(o * np.log(c) + (np.array([1]) - o) * np.log(np.array([1]) - c)), decimals=5)
pn = np.array(predicted_cls)
gn = np.array(gt_cls)
print(f"自定义实现的结果: {bce(pn, gt_cls)}")
"""
PyTorch官方实现的结果: [[0.10536 1.60944 0.10536]
[0.22314 1.20397 0.22314]]
自定义实现的结果: [[0.10536 1.60944 0.10536]
[0.22314 1.20397 0.22314]]
"""
可以看到,官方实现和这里的公式的输出结果是一致的,因此这里的类别损失公式是正确的。
3.7.3 定位损失(Location Loss)
L loc ( t , g ) = 1 N pos ∑ i ∈ pos ( σ ( t x i ) − g ^ x i ) 2 + ( σ ( t y i ) − g ^ y i ) 2 + ( t w i − g ^ w i ) 2 + ( t h i − g ^ h i ) 2 g ^ x i = g x i − c x i g ^ y i = g y i − c y i g ^ w i = ln g w i p w i g ^ h i = ln g h i p h i \begin{aligned} & L_{\text{loc}}(t, g)= \frac{1}{N_{\text{pos}}} \sum_{i\in \text{pos}}(\sigma(t^i_x) - \hat g^i_x)^2 + (\sigma(t^i_y) - \hat g^i_y)^2 + (t^i_w - \hat g^i_w)^2 + (t^i_h - \hat g^i_h)^2 \\ & \hat g^i_x = g^i_x - c^i_x \\ & \hat g^i_y = g^i_y - c^i_y \\ & \hat g^i_w = \ln \frac{g^i_w}{p^i_w} \\ & \hat g^i_h = \ln \frac{g^i_h}{p^i_h} \\ \end{aligned} Lloc(t,g)=Npos1i∈pos∑(σ(txi)−g^xi)2+(σ(tyi)−g^yi)2+(twi−g^wi)2+(thi−g^hi)2g^xi=gxi−cxig^yi=gyi−cyig^wi=lnpwigwig^hi=lnphighi
其中:
- t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th为网络预测的回归参数
- g x , g y , g w , g h g_x, g_y, g_w, g_h gx,gy,gw,gh为GTBox中心点坐标和宽度、高度(映射在grid cell中的)
- c x , c y , p w , p h c_x, c_y, p_w, p_h cx,cy,pw,ph为该grid cell的左上角坐标和宽度、高度

在训练阶段,定位损失使用的是平方误差和损失(也就是我们常说的 L 2 L_2 L2损失)。
- t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th为预测的关于anchor的偏移量
- σ ( ⋅ ) \sigma(\cdot) σ(⋅)为Sigmoid函数 —— 将输入映射到 [ 0 , 1 ] [0, 1] [0,1]
- p w , p h p_w, p_h pw,ph为先验框的宽度和高度
- b x , b y , b w , b h b_x, b_y, b_w, b_h bx,by,bw,bh为最终边界框的中心点坐标以及宽度、高度
- c x , c y c_x, c_y cx,cy当前grid cell左上角点的坐标
这里的定位损失函数做一个简单了解就可以了,因为后面的v3-SPP、v4、v5并不是使用平方误差和来计算定位损失,而是使用的CIoU Loss。
4. YOLO v3-SPP
4.1 v3-SPP相比v3的改进之处
性能对比:
| Model | 输入图片尺寸 | COCO mAP@0.5:0.95 | COCO mAP@0.5 |
|---|---|---|---|
| YOLO v3 | 512×512 | 32.7 | 57.7 |
| YOLO v3-SPP | 512×512 | 35.6 (+2.90) | 59.5 (+1.80) |
| YOLO v3-SPP-ultralytics | 512×512 | 42.6 (+9.90) | 62.4 (+4.70) |
ultralytics的YOLO v3-SPP之所以性能提升更多是因为使用了更多的trick
tricks:
- Mosaic图像增强
- SPP模块(Spatial Pyramid Pooling,空间金字塔池化)
- CIoU Loss
- Focal Loss(焦点损失)
前三个是ultralytics使用的,Focal Loss虽然在网络有已经实现了,但默认不使用(效果并不是很好)
4.2 Mosaic图像增强
之前我们也使用过很多图像增强算法,如:
- 随机裁剪
- 随机水平翻转
- 亮度、色度、饱和度随机调整
- …
在ultralytics的YOLO v3中,Mosaic图像增强的实现就是将几张图片拼接在一起(默认使用4张图片)。
4.2.1 Mosaic图像增强的优点
- 增加数据的多样性
- 增加目标个数 —— 一张图片中可能目标的个数是很少的,Mosaic之后目标的个数增加了,有助于网络的训练
- BN能一次性统计多张图片的参数 —— Batch size越大,BN的统计值就越接近整个数据集的均值和方差(越准),效果就越好。但有时我们的设备性能受限,BS不能增大。如果将多张图片拼接在一起再输入进网络,变增加了输入网络的BS。比如:输入一张由四张图片拼接的图像,等效于并行输入四张原始图片(BS=4)。通过Mosaic图像增强算法,输入一张图片就包含了4张图片的均值和方差,所以对于BN统计均值和方差是有一定帮助的。
4.3 SPP模块
4.3.1 SPP模块与SPPnet的区别与联系
YOLO v3-SPP中的SPP并不是SPPnet中的SPP结构,而是借鉴SPPnet中SPP的结构。二者是不一样的
SPP: Spatial Pyramid Pooling,空间金字塔池化
4.3.2 SPP在YOLO v3中的位置
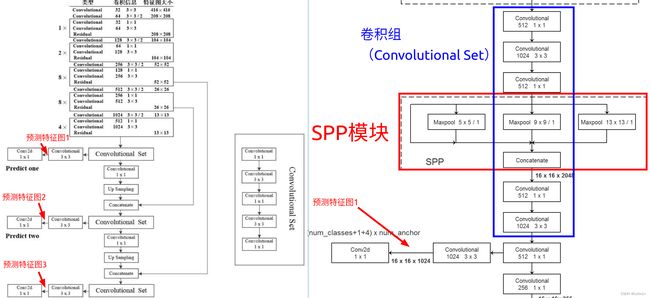
对比YOLO v3的原网络,YOLO v3-SPP将v3中的Convolutional Set拆开了,中间插入了SPP模块,剩下的都是一样的。
4.3.3 SPP模块详解
- 直接接到输出(类似于identity结构)
- 5×5的MaxPooling(stride=1)—— 特征图shape不变(C, H, W均不变)
- 9×9的MaxPooling(stride=1)—— 特征图shape不变(C, H, W均不变)
- 13×13的MaxPooling(stride=1)—— 特征图shape不变(C, H, W均不变)
最后再经过concat进行维度拼接,得到SPP的输出特征图 —— 即经过SPP模块,特征图的shape不变,channel变为原来的4倍。
这里三个分支的MaxPooling的步距均为1意味着在做池化之前会对特征图进行padding
4.3.4 SPP模块的目的
实现不同尺度特征图的特征融合。
虽然SPP模块看起来非常简单,但该模块对网络整体性能带来了比较大的提升。
4.3.5 SPP模块的个数
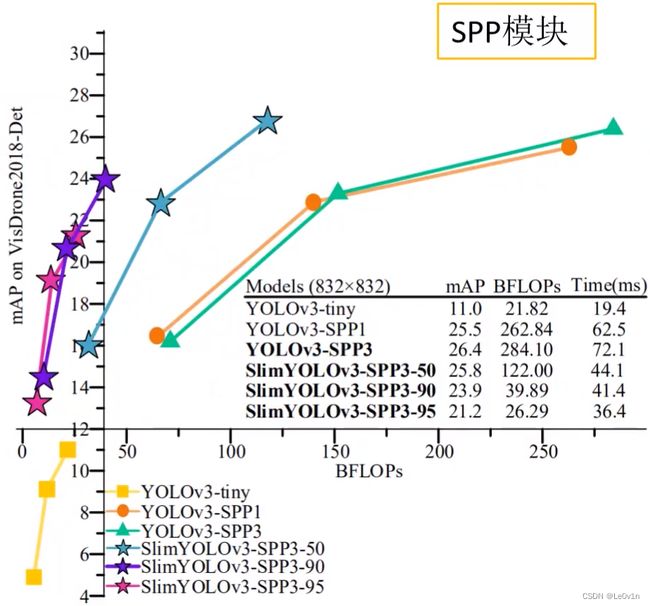
Q:为什么只在第一个预测特征图前加SPP模块,其他两个预测特征图前可以加SPP模块吗?
A:实际操作中是可以的,但是这样做有必要吗?我们看一下面这张图。
其中:
- YOLOv3-SPP1为只添加了一个SPP模块的YOLO v3
- YOLOv3-SPP3为添加了三个SPP模块的YOLO v3
在输入图像尺度比较小的情况下,YOLOv3-SPP1比YOLOv3-SPP3要好一些,但随着输入图片尺度的增大,YOLOv3-SPP3的效果优于SPP1。
mAP提高0.9%,但推理速度增加9.6 ms —— 建议使用YOLO v3-SPP1
4.4 定位损失 —— L2、IoU、GIoU、DIoU、CIoU
4.4.1 YOLO v3原始的损失
YOLO v3原始的定位损失是squared error loss,平方和损失(也就是我们常说的 L 2 L_2 L2损失)。
4.4.2 流行的定位损失 —— 带有IoU字段
现在好用的定位损失是带有IoU字段的损失:
- IoU Loss
- GIoU Loss
- DIoU Loss
- CIoU Loss
发展历程如下:
回顾一下IoU的计算公式:—— 这只是IoU计算公式,并非Loss计算公式
I o U = a r e a ( C ) ∩ a r e a ( G ) a r e a ( C ) ∪ a r e a ( G ) \mathrm{IoU = \frac{area(C) \cap area(G)}{area(C) \cup area(G)}} IoU=area(C)∪area(G)area(C)∩area(G)
4.4.3 IoU Loss
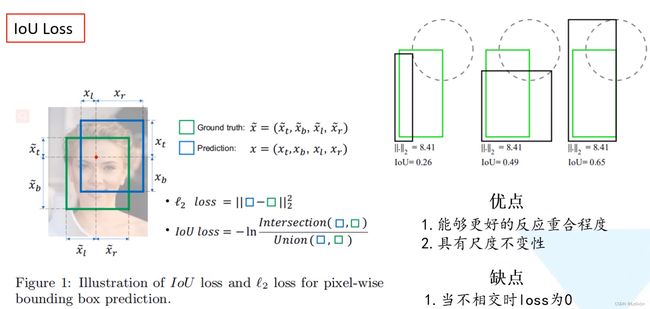
- 绿色为GTBox
- 黑色为预测边界框
- ∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||_2 ∣∣⋅∣∣2为L2损失值
- IoU为IoU值
右上角的图展示了3组矩形框重合的示例。我们发现最后一组矩形框预测的IoU效果是最好的,但这三组的L2损失都是一样的,均为8.41 —— 这说明L2损失不能很好的反应预测边界框与GTBox的重合程度。
基于该问题,引入了IoU Loss,公式为:—— 基于IoU的Loss计算公式
L I o U = − ln IoU = ln IoU − 1 = ln 1 IoU = 1 − ln IoU \begin{aligned} L_\mathrm{IoU} & = - \ln \text{IoU} \\ & =\ln \text{IoU}^{-1} \\ & =\ln \frac{1}{\text{IoU}} \\ & = 1 - \ln \text{IoU} \end{aligned} LIoU=−lnIoU=lnIoU−1=lnIoU1=1−lnIoU
IoU Loss的优点: 相比L2 Loss
- 能够更好的反映出重合程度
- 具有尺度不变性 —— 无论两个矩形框是大是小,它的重合程度与矩形框的尺度是无关的
IoU Loss的优点:
3. 当两个矩形框不相交时,Loss为0 —— 不相交,IoU值为0,进而Loss值也为0 -> 无法反向传播损失
0 ≤ I o U ≤ 1 0\le IoU \le 1 0≤IoU≤1,因此IoU为0时无法完成反向传播!
4.4.4 GIoU Loss
论文题目:Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
论文地址:https://arxiv.org/abs/1902.09630
GIoU = Generalized IoU
generalized 英
[ˈdʒenrəlaɪzd]美[ˈdʒenrəlaɪzd]
adj. 笼统的; 普遍的; 概括性的; 全面的;
v. 概括; 归纳; 笼统地讲; 概括地谈论; 扩大…的运用; 将…类推到(较大的范围);
![]()
其中:
- 绿色为GTBox
- 红色为预测边界框
- 蓝色为预测边界框和GTBox的最小矩阵,它的面积为 A c A^c Ac
4.4.4.1 GIoU计算公式
GIoU公式: —— 这只是GIoU的定义公式,并非Loss计算公式
G I o U = I o U − A c − u A c = I o U − 最 小 外 接 矩 形 面 积 − 预 测 边 界 框 ∪ GTBox 最 小 外 接 矩 形 面 积 \begin{aligned} \mathrm{GIoU} & = \mathrm{IoU} - \frac{A^c-u}{A^c} \\ & = \mathrm{IoU} - \frac{最小外接矩形面积 - 预测边界框 \cup \text{GTBox}}{最小外接矩形面积} \end{aligned} GIoU=IoU−AcAc−u=IoU−最小外接矩形面积最小外接矩形面积−预测边界框∪GTBox
− 1 ≤ G I o U ≤ 1 -1 \le \mathrm{GIoU} \le 1 −1≤GIoU≤1
其中:
- A c A^c Ac为最小外接矩形的面积
- u u u为预测边界框与GTBox并集 ∪ \cup ∪的面积
- 当这两个矩形框完美地重合在一起时, A c = u = 矩 形 框 的 面 积 A^c = u = 矩形框的面积 Ac=u=矩形框的面积,所以公式中 A c − u A c \frac{A^c-u}{A^c} AcAc−u的分子等于0,即惩罚项没有了,IoU=1,此时的GIoU=1
- 当这两个矩形框距离无穷远时, A c → ∞ A^c \rightarrow \infty Ac→∞, u → 常 数 u \rightarrow 常数 u→常数,此时 A c − u A c → 1 \frac{A^c-u}{A^c} \rightarrow 1 AcAc−u→1,而且它俩的 IoU = 0 \text{IoU} = 0 IoU=0,所以此时的GIoU=-1
因此GIoU的下限和上限为-1和1。即便GIoU=-1也可以实现梯度的反向传播。
4.4.4.2 GIoU Loss计算公式
GIoU Loss公式: —— 基于GIoU的Loss计算公式
L GIoU = 1 − GIoU L_{\text{GIoU}} = 1 - \text{GIoU} LGIoU=1−GIoU
0 ≤ L GIoU ≤ 2 0 \le L_{\text{GIoU}} \le 2 0≤LGIoU≤2
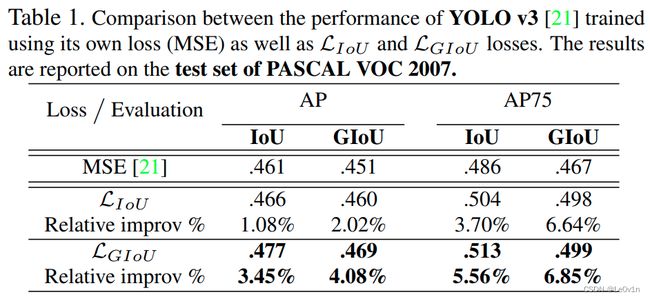
4.4.4.3 IoU与GIoU在YOLO v3上mAP对比
4.4.4.4 GIoU退化为IoU的情况
当①预测框和GTBox完全重合时或②预测框在GTBox的内部,IoU和GIoU的损失值Loss都一样,此时GIoU退化为IoU -> GIoU=IoU。
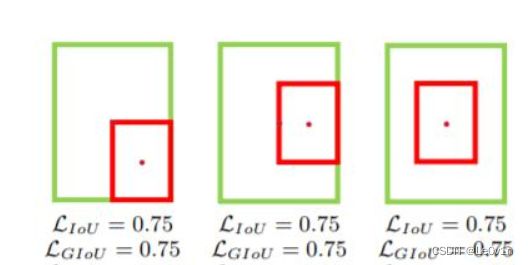
Case 1:预测框和GTBox完全重合
L GIoU = 1 − GIoU = 1 − I o U + 最 小 外 接 矩 形 面 积 − 预 测 边 界 框 ∪ GTBox 最 小 外 接 矩 形 面 积 = 1 − I o U + G T B o x − A n c h o r ∪ G T B o x G T B o x = 1 − I o U + G T B o x − G T B o x G T B o x = 1 − I o U = L IoU \begin{aligned} L_{\text{GIoU}} & = 1 - \text{GIoU} \\ & = 1 - \mathrm{IoU} + \frac{最小外接矩形面积 - 预测边界框 \cup \text{GTBox}}{最小外接矩形面积} \\ & = 1 - \mathrm{IoU} + \mathrm{\frac{GTBox - Anchor \cup GTBox}{GTBox}} \\ & = 1 - \mathrm{IoU} + \mathrm{\frac{GTBox - GTBox}{GTBox}} \\ & = 1 - \mathrm{IoU}\\ & = L_{\text{IoU}} \end{aligned} LGIoU=1−GIoU=1−IoU+最小外接矩形面积最小外接矩形面积−预测边界框∪GTBox=1−IoU+GTBoxGTBox−Anchor∪GTBox=1−IoU+GTBoxGTBox−GTBox=1−IoU=LIoU
Case 2:预测框在GTBox的内部
L GIoU = 1 − GIoU = 1 − I o U + 最 小 外 接 矩 形 面 积 − 预 测 边 界 框 ∪ GTBox 最 小 外 接 矩 形 面 积 = 1 − I o U + G T B o x − A n c h o r ∪ G T B o x G T B o x = 1 − I o U + G T B o x − G T B o x G T B o x = 1 − I o U = L IoU \begin{aligned} L_{\text{GIoU}} & = 1 - \text{GIoU} \\ & = 1 - \mathrm{IoU} + \frac{最小外接矩形面积 - 预测边界框 \cup \text{GTBox}}{最小外接矩形面积} \\ & = 1 - \mathrm{IoU} + \mathrm{\frac{GTBox - Anchor \cup GTBox}{GTBox}} \\ & = 1 - \mathrm{IoU} + \mathrm{\frac{GTBox - GTBox}{GTBox}} \\ & = 1 - \mathrm{IoU}\\ & = L_{\text{IoU}} \end{aligned} LGIoU=1−GIoU=1−IoU+最小外接矩形面积最小外接矩形面积−预测边界框∪GTBox=1−IoU+GTBoxGTBox−Anchor∪GTBox=1−IoU+GTBoxGTBox−GTBox=1−IoU=LIoU
最终GIoU在这种情况下还是无法区分预测框和GTBox的位置关系,也导致此时的边界框回归收敛很慢。
4.4.5 DIoU Loss
论文题目:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
论文地址:https://arxiv.org/abs/1911.08287
DIoU: Distance IoU
在这篇论文中,作者认为IoU Loss和GIoU Loss存在两个问题:
- 收敛特别慢
- 回归不够准确
所以这篇论文主要围绕着两个主题:
- 如何更快让Loss收敛
- 如何达到更高的定位精度
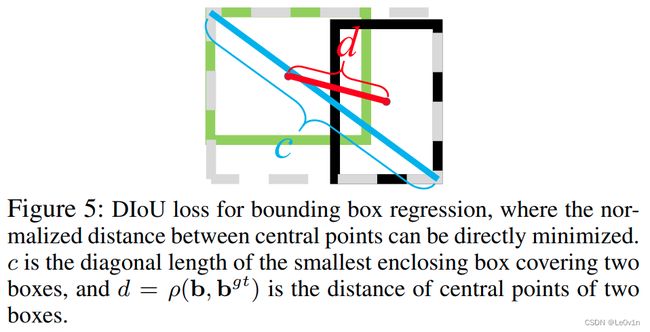
4.4.5.1 DIoU的计算公式 —— 并非Loss计算公式
D I o U = I o U − ρ 2 ( b , b gt ) c 2 = I o U − d 2 c 2 \begin{aligned} \mathrm{DIoU} & = \mathrm{IoU} - \frac{\rho^2(b, b^{\text{gt}})}{c^2} \\ & = \mathrm{IoU} - \frac{d^2}{c^2} \end{aligned} DIoU=IoU−c2ρ2(b,bgt)=IoU−c2d2
− 1 ≤ D I o U ≤ 1 -1 \le \mathrm{DIoU} \le 1 −1≤DIoU≤1
其中:
- b , b g t b, b^{\mathrm{gt}} b,bgt分别为预测目标边界框的中心坐标,GTBox的中心坐标
- ρ 2 \rho^2 ρ2表示目标预测边界框与GTBox之间的欧氏距离
- d d d为Anchor与GTBox中心点的距离
- c c c最小外接矩形的对角线长度
上限和下线:
- 当两个矩形框完美重合:二者的欧氏距离为0,即 D I o U = I o U = 1 \mathrm{DIoU = IoU} = 1 DIoU=IoU=1
- 当两个矩形框距离无限远时,二者的欧式距离→ ∞ \infty ∞,最小外接矩形的对角线长度也→ ∞ \infty ∞,所以 D I o U = I o U − 1 = − 1 \mathrm{DIoU = IoU - 1} = -1 DIoU=IoU−1=−1(此时IoU=0)
4.4.5.2 DIoU Loss计算公式 —— Loss计算公式
L D I o U = 1 − DIoU L_{\mathrm{DIoU}} = 1 - \text{DIoU} LDIoU=1−DIoU
0 ≤ L D I o U ≤ 2 0 \le L_{\mathrm{DIoU}} \le 2 0≤LDIoU≤2
4.4.5.3 DIoU Loss的优势
通过4.4.5.1和4.4.5.2中两个公式完美可以发现,DIoU Loss可以直接最小化(minimize)两个boxes之间的距离,因此收敛速度更快。
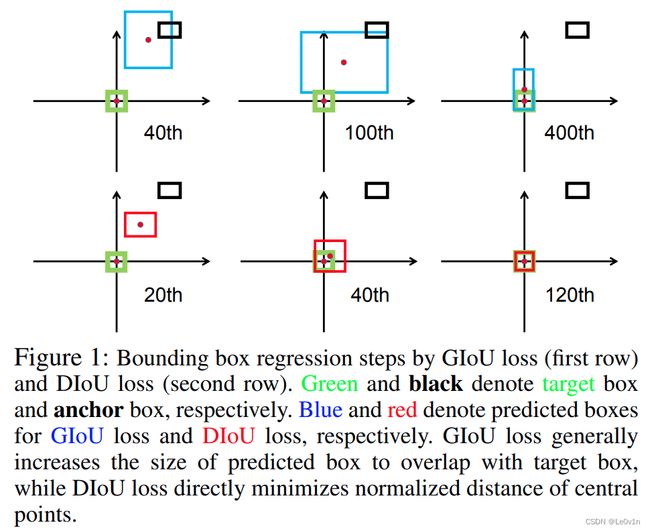
4.4.5.4 DIoU与GIoU的对比
- 黑色为Anchor priors
- 绿色为GTBox
- 蓝色为GIoU的预测目标边界框
- 红色为DIoU的预测目标边界框
- 第一行为使用GIoU训练网络
- 第二行为使用DIoU训练网络
可以看到,GIoU收敛速度慢且最终的效果也并不是很好;DIoU收敛速度快,在120个迭代就可以完美收敛,效果非常好。
4.4.5.5 DIoU解决GIoU退化为IoU的效果
前面我们说过,当预测目标边界框在GTBox内部时,GIoU会退化为IoU,我们看一下DIoU在这种情况下的效果。

可以看到,在这种情况下,DIoU并没有退化为IoU。
4.4.5.6 三种定位Loss计算公式对比
这里我们先忽略CIoU
4.4.6 CIoU Loss
作者在讲完DIoU Loss之后又引出了CIoU Loss。作者认为,一个优秀的回归定位损失应该考虑3种几何参数:
- 重叠面积 —— IoU
- 中心点距离 —— ρ 2 ( b , b gt ) c 2 \frac{\rho^2(b, b^{\text{gt}})}{c^2} c2ρ2(b,bgt)
- 长宽比 —— α υ \alpha \upsilon αυ
4.4.6.1 CIoU计算公式 —— 非Loss计算公式
C I o U = I o U − ( ρ 2 ( b , b gt ) c 2 + α υ ) υ = 4 π 2 ( arctan w gt h gt − arctan w h ) 2 α = υ ( 1 − IoU ) + υ \mathrm{CIoU} = \mathrm{IoU} - (\frac{\rho^2(b, b^{\text{gt}})}{c^2} + \alpha \upsilon) \\ \upsilon = \frac{4}{\pi^2}(\arctan \frac{w^{\text{gt}}}{h^{\text{gt}}} - \arctan \frac{w}{h})^2 \\ \alpha = \frac{\upsilon}{(1 - \text{IoU}) + \upsilon} CIoU=IoU−(c2ρ2(b,bgt)+αυ)υ=π24(arctanhgtwgt−arctanhw)2α=(1−IoU)+υυ
其中:
- w , h w, h w,h为矩形框的宽度和高度
这样CIoU将长宽比这个因素引入进来了 —— 相比DIoU考虑的更加全面。
4.4.6.2 CIoU Loss计算公式 —— Loss计算公式
L CIoU = 1 − CIoU L_{\text{CIoU}} = 1 - \text{CIoU} LCIoU=1−CIoU
4.4.6.3 CIoU与其他IoU字段的损失函数效果对比
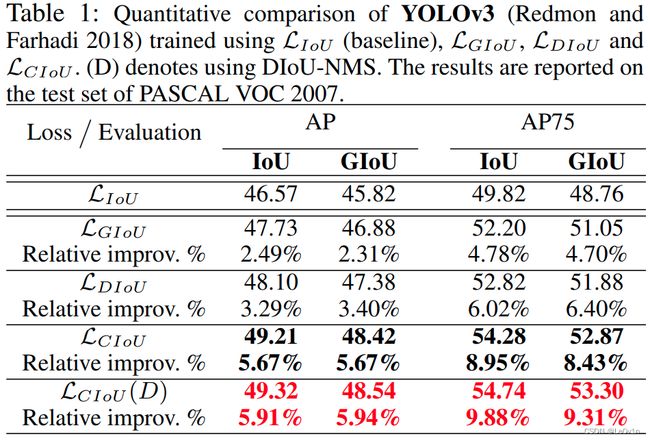
其中:
L CIoU ( D ) \mathcal{L}_{\text{CIoU}}(D) LCIoU(D)如果用DIoU替换IoU,那么CIoU还有进一步的提升。
虽然提升很小,但是使用DIoU替换CIoU是更加合理的,因为重叠的情况下,IoU和GIoU是没办法评价两个矩形框的重合关系(退化问题),而DIoU可以解决退化的问题。
所以现在有很多Post-process(后处理算法)中将IoU替换为了DIoU。
4.4.6.4 DIoU与CIoU的关系
这篇论文中,作者提出了两个IoU算法,其中:
- DIoU的目的是替换IoU
- CIoU的目的是替换IoU Loss。
4.4.6.5 CIoU与GIoU检测效果示例
4.4.7 这几种IoU Loss该如何选择
有时候CIoU的效果可能不如GIoU和DIoU -> 深度学习, 炼丹
4.5 Focal Loss
论文题目:Focal Loss for Dense Object Detection
论文地址:https://arxiv.org/abs/1708.02002
4.5.1 Focal Loss的争议
这个trick的争议比较大,有些人说Focal Loss是有用的,有些人觉得它没有任何作用。
在YOLO v3原论文中,作者尝试去使用Focal Loss,但掉了2个点 —— Joseph Redmon也感到很好奇。
我们尝试使用焦点损失。 它使我们的 mAP 下降了大约 2 个点。 YOLOv3 可能已经对焦点损失试图解决的问题具有鲁棒性,因为它具有单独的对象预测和条件类预测。 因此,对于大多数示例,类别预测没有损失? 或者其他的东西? 我们不完全确定。
![]()
- 第一行 γ = 0 \gamma=0 γ=0,可以认为没有使用Focal Loss的损失计算方法
- 使用Focal Loss之后,AP最高达到34,提升了越3个点
4.5.2 Focal Loss的使用场景
在论文中作者认为Focal Loss主要针对:
- One-stage目标检测模型(SSD、YOLO)
- 正负样本不平衡(Class Imbalance)
4.5.3 正负样本不平衡
一张图片中能够匹配到GTBox的目标候选框(正样本)个数一般只有十几个或几十个,而没有匹配到GTBox的目标候选框(负样本)大概有 1 0 4 − 1 0 5 10^4 - 10^5 104−105个(上万个或十几万个)。
- 红色的框是没有匹配到目标的
- 黄色的框是匹配到目标的
所以grid cell生成的Anchor在匹配GTBox的时候绝大多数都是没有匹配到目标的 —— 负样本数量远大于正样本数量
Q:Two-stage网络为什么没有提及到正负样本不平衡问题呢?
A:Two-stage网络分两步走,在第一步中类别不均衡的问题肯定是有的,但最终的结果是通过第二阶段的检测完成的。在Faster R-CNN中,通过RPN最终提供给第二阶段的候选框也就2000多个。相比One-stage网络的grid cell生成的候选框就很多了(上万个、十几万个)而言,2000个候选框就显得正负样本不平衡现象就好很多了。
在这上万个、上十万个未匹配到目标候选框的中,大部分都是简单易分的负样本。这些简单易分的负样本虽然对网络训练起不到什么作用,但由于数量太多会淹没少量但有助于网络训练的样本。
比如我们直接使用所有的样本(不丢弃负样本)去训练网络,如果在一张图片中匹配到了50个正样本,每个正样本共享的损失为3,则正样本的总损失为 3 × 50 = 150 3 \times 50=150 3×50=150。假如有100,000个易分的负样本,它们每一个共享的损失为0.1,那么负样本总损失为 100 , 000 × 0.1 = 10 , 000 100,000 \times 0.1 = 10,000 100,000×0.1=10,000。这种情况下,正样本的损失在负样本的损失面前就没有什么话语权了。
因此如果直接使用所有的样本去训练网络,那么负样本的损失会淹没正样本的损失 —— 模型的训练效果会很差。
Q:在之前讲的网络当中不是会筛选正负样本吗?
A:我们之前筛选正负样本的策略称为hard negative mining(负硬挖掘) —— 不会使用所有的负样本训练网络,而是选取损失比较大的负样本去训练网络 —— 这样的策略确实是有效果的,而且网络训练效果也还可以。
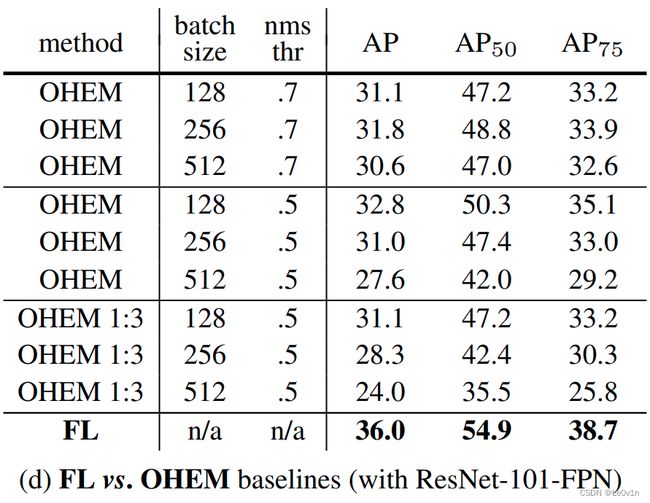
前面这些方法都是hard negative mining方法,而本文提出的Focal Loss效果比hard negative mining要好(比hard negative mining最好的方法多3个点)。
那么Focal Loss的效果为什么这么好呢?接下来我们分析其理论。
4.5.4 计算CE Loss(交叉熵损失)

Focal Loss 旨在解决单阶段目标检测场景,其中在训练期间前景和背景类之间存在极端不平衡(例如, 1 : 1000 1:1000 1:1000)。 我们从二元分类的交叉熵(CE)损失开始引入焦点损失:
CE ( p , y ) = { − ln p if y = 1 ( 当 候 选 框 为 正 样 本 ) , − ln ( 1 − p ) otherwise ( 当 候 选 框 为 负 样 本 ) \text{CE}(p, y) = \begin{cases} -\ln p & \text{if} \ \ y=1(当候选框为正样本),\\ -\ln (1-p) & \text{otherwise}(当候选框为负样本) \end{cases} CE(p,y)={−lnp−ln(1−p)if y=1(当候选框为正样本),otherwise(当候选框为负样本)
在上面的 y ∈ { ± 1 } y \in \{±1\} y∈{±1} 中指定了 ground-truth 类(1为正样本,-1为负样本), p ∈ [ 0 , 1 ] p \in [0, 1] p∈[0,1] 是模型对标签 y = 1 y = 1 y=1 的类的估计概率。为了符号方便,我们定义 p t p_t pt:
p t = { p if y = 1 ( 当 候 选 框 为 正 样 本 ) , 1 − p otherwise ( 当 候 选 框 为 负 样 本 ) p_t = \begin{cases} p & \text{if} \ \ y=1(当候选框为正样本),\\ 1-p & \text{otherwise}(当候选框为负样本) \end{cases} pt={p1−pif y=1(当候选框为正样本),otherwise(当候选框为负样本)
所以 CE ( p , y ) \text{CE}(p, y) CE(p,y)可以被简化为:
CE ( p , y ) = CE ( p t ) = − ln ( p t ) \text{CE}(p, y) = \text{CE}(p_t) = −\ln(p_t) CE(p,y)=CE(pt)=−ln(pt)
4.5.5 引入 α \alpha α加权因子后对计算交叉熵损失CE Loss的影响
- 为类别 1 (正样本)y=1引入加权因子 α ∈ [ 0 , 1 ] α ∈ [0, 1] α∈[0,1]
- 为类别 -1 (负样本)y=-1引入加权因子 1 − α 1-α 1−α。
在实践中, α α α 可以通过逆类频率设置,也可以作为超参数通过交叉验证来设置。 为了符号方便,我们定义 α t α_t αt 的方式与定义 p t p_t pt 的方式类似。 我们将 α α α 平衡 CE 损失写为:
C E ( p t ) = − α t ln ( p t ) \mathrm{CE}(p_t) = -\alpha_t \ln(p_t) CE(pt)=−αtln(pt)
这种损失是对 CE 的简单扩展,我们将其视为我们提出的焦点损失的实验基线(baseline)。
下表展示了当 α \alpha α取不同值时的AP:
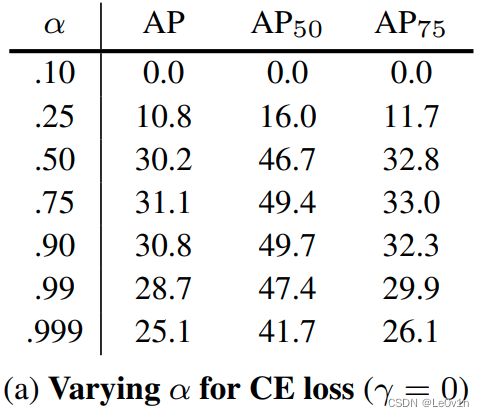
从表中可以发现,当 α = 0.75 时 \alpha=0.75时 α=0.75时,AP是最好的
Note:
- α \alpha α并不是正负样本的比例
- 当 α = 0.75 时 \alpha=0.75时 α=0.75时,AP是最好的,而一般正负样本的比例是 1 : 1000 1:1000 1:1000,怎么可能是0.75
- 所以这里的 α \alpha α就是一个超参数 —— 用来平衡正负样本的权重,并不是正负样本的比例。
4.5.6 为CE Loss引入新的因子 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ

正如我们的实验将表明的那样,在密集检测器的训练过程中遇到的大量类别不平衡(正负样本不平衡)问题压倒了交叉熵损失(CE Loss),表现为容易分类的负样本构成了损失的大部分,并主导了梯度。 虽然 α α α:
- 平衡了正例/负例的权重(重要程度)
- 但它并没有区分容易/困难的样本
相反,我们建议重塑损失函数以降低简单示例的权重,从而将训练重点放在难的负样本(hard negatives)上。
更正式地说,我们建议在交叉熵损失中添加:
- 调制因子(modulating factor): ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ
- 可调聚焦参数(tunable focusing parameter): γ ≥ 0 \gamma ≥ 0 γ≥0。
我们将焦点损失(Focal Loss)定义为:
Focal Loss ( p t ) = − ( 1 − p t ) γ ln ( p t ) \text{Focal Loss}(p_t) = -(1-p_t)^\gamma \ln(p_t) Focal Loss(pt)=−(1−pt)γln(pt)
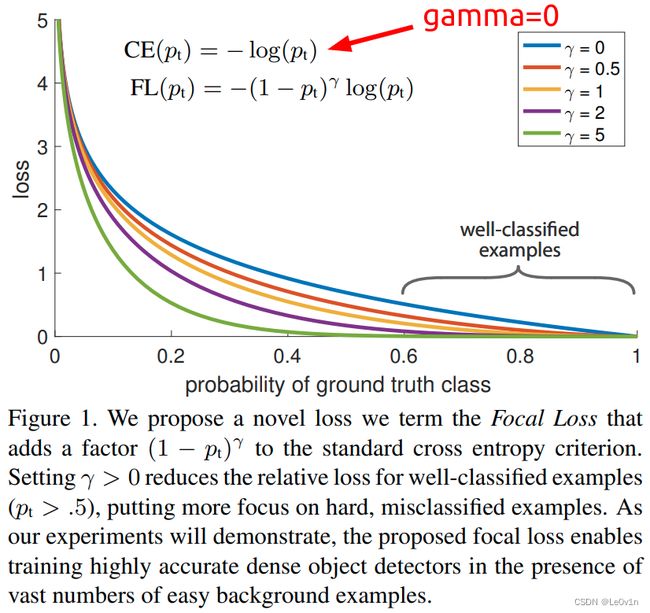
图 1. 我们提出了一种新的损失,我们称之为 Focal Loss,它在标准交叉熵标准中增加了一个因子 ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ。 设置 γ > 0 γ > 0 γ>0 可减少易分样本(简单样本)(pt > .5)的相对损失,将更多注意力放在难分类的错误示例上。 正如我们的实验将证明的那样,所提出的焦点损失能够在存在大量简单背景示例的情况下训练高度准确的密集对象检测器。
上图展示了 γ ∈ [ 0 , 5 ] γ ∈ [0, 5] γ∈[0,5] 的几个值,Focal Loss的效果。
当 γ = 0 \gamma=0 γ=0时,Focal Loss就是CE Loss
其中:
横坐标就是 p t p_t pt, p t = { p if y = 1 ( 当 候 选 框 为 正 样 本 ) , 1 − p otherwise ( 当 候 选 框 为 负 样 本 ) p_t = \begin{cases} p & \text{if} \ \ y=1(当候选框为正样本),\\ 1-p & \text{otherwise}(当候选框为负样本) \end{cases} pt={p1−pif y=1(当候选框为正样本),otherwise(当候选框为负样本)。
- 如果是正样本,我们希望 p p p越大越好 —— 越准确 —— p t p_t pt越大越好
- 如果是负样本,我们希望 p p p越小越好 —— 也就是 1 − p 1-p 1−p越大越好—— p t p_t pt越大越好
不管是正样本还是负样本,我们都希望 p t p_t pt越大越好。所以当横坐标的值处于 [ 0.6 , 1 ] [0.6, 1] [0.6,1]之间属于分类效果比较好的情况。这部分分类效果比较好的样本,它们就属于很容易分辨的样本,即简单的样本。对于这些容易的样本,我们没必要在它们身上放置很大的权重(具体体现就是loss,我们没必要完全接收它返回的loss,所以给它的loss加一个权重,让它们的loss不那么大,这在纵坐标上也能体现出来)。所以:
- 当 γ > 0 \gamma \gt 0 γ>0时,随着 p t p_t pt的增大,Loss下降越来越快,这意味着 γ \gamma γ越大,对于易分样本的权重就越小。
- 但 γ \gamma γ并不是越大越好,当 γ = 5 \gamma = 5 γ=5时, p t = 0.4 p_t=0.4 pt=0.4时, p t = 0.4 p_t=0.4 pt=0.4位置的样本并不属于简单的样本,对于一个不是简单的样本,我们降低它loss的权重是不对的。
总之:
( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ这个因子能够降低易分样本的损失权重(贡献) —— 这也是Focal Loss核心的部分。
以下是论文中对这张图的分析:
我们注意到Focal Loss的两个属性。
- 当一个样本被错误分类并且 p t p_t pt很小时,调制因子 ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ接近1,损失不受影响。 当 p t p_t pt → 1 时,调制因子 ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ变为 0,并且分类良好的示例(易检测样本)的损失被降低权重。
- 聚焦参数 γ γ γ 平滑地调整了简单示例(易检测样本)被降低权重的速率。 当 γ = 0 γ = 0 γ=0 时,FL 等效于 CE,并且随着 γ γ γ 的增加,调制因子 ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ的效果同样增加(我们发现 γ = 2 γ = 2 γ=2 在我们的实验中效果最好)。
直观地说,调制因子 ( 1 − p t ) γ (1 - p_t)^\gamma (1−pt)γ减少了简单示例的损失贡献(权重),并扩展了示例接收低损失的范围。 例如,在 γ = 2 γ = 2 γ=2 的情况下,与 CE 相比,
- 分类为 p t = 0.9 p_t = 0.9 pt=0.9 的样本的损失将降低 100 倍,
- 而 p t ≈ 0.968 p_t ≈ 0.968 pt≈0.968 分类的示例的损失将降低 1000 倍。
这反过来又增加了纠正错误分类示例的重要性(对于 p t ≤ . 5 p_t ≤ .5 pt≤.5 和 γ = 2 γ = 2 γ=2,其损失最多缩小 4 倍)。
自己的理解:
我们看上面那张图:
- 横坐标是 p t p_t pt,就是识别该样本的概率,越向右说明该样本识别的准确率越高 —— 该样本越简单。
- 纵坐标是loss,不同的准确率( p t p_t pt)有不同的loss
如果使用CE,我们发现在[0.6, 1]这个区间内, loss是最高的,即这个区间内准确率高的样本loss所占的权重也大。但对于Focal Loss来说,随着 γ \gamma γ的增加,[0.6, 1]这个区间内loss的值在减少,说明减少了在该区间内loss的权重。又因为这个区间属于易识别的样本,所以就减少了易识别样本loss的权重。这样就实现了网络更加关注难识别样本的目的。
γ 也 不 能 一 味 的 增 大 , 例 如 \gamma也不能一味的增大,例如 γ也不能一味的增大,例如\gamma=5 时 , 对 于 时,对于 时,对于p_t=0.4$,这个概率下样本并不是属于易检测样本,所以权重不应该减少那么多!
4.5.7 Focal Loss最终公式 —— 将 α \alpha α和 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ引入CE
在实践中,我们使用焦点损失的 α 平衡变体:
Focal Loss ( p t ) = − α t ( 1 − p t ) γ ln ( p t ) \text{Focal Loss}(p_t) = -\alpha_t(1-p_t)^\gamma \ln(p_t) Focal Loss(pt)=−αt(1−pt)γln(pt)
我们在我们的实验中采用这种形式,因为它比非 α α α 平衡形式略微提高了准确性。 最后,我们注意到损失层的实现将计算 p p p 的 sigmoid 操作与损失计算相结合,从而提高了数值稳定性。
虽然在我们的主要实验结果中我们使用了上面的焦点损失定义,但它的精确形式并不重要。 在附录中,我们考虑了焦点损失的其他实例,并证明这些实例同样有效。
下面给出Focal Loss的展开公式:
L FL ( p ) = { − α ( 1 − p ) γ ln ( p ) if y = 1 − ( 1 − α ) p γ ln ( 1 − p ) otherwise L_{\text{FL}}(p) = \begin{cases} -\alpha(1-p)^\gamma \ln(p) & \text{if} \ \ y = 1 \\ -(1-\alpha)p^\gamma \ln(1-p) & \text{otherwise} \end{cases} LFL(p)={−α(1−p)γln(p)−(1−α)pγln(1−p)if y=1otherwise
4.5.8 不同 α , γ \alpha, \gamma α,γ所对应的AP情况
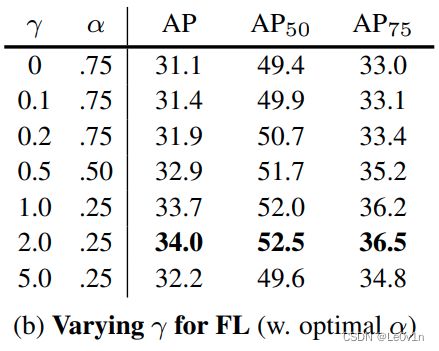
当 γ = 2.0 , α = 0.25 \gamma = 2.0, \alpha = 0.25 γ=2.0,α=0.25时,AP是最好的。
所以这里的 α \alpha α认为是一个超参数即可,不要认为它是用来平衡正负样本权重。
4.5.9 [例子] Focal Loss与CE的对比
| No | p p p | y | p t = { p if y = 1 , 1 − p otherwise p_t =\begin{cases}p & \text{if} \ \ y=1,\\1-p & \text{otherwise}\end{cases} pt={p1−pif y=1,otherwise | CE Loss | FL ( γ = 2 , α = 0.25 \gamma=2, \alpha=0.25 γ=2,α=0.25) | rate |
|---|---|---|---|---|---|---|
| 行 | 概率 | 正负样本 | 难易程度 | 交叉熵损失 | Focal损失 | FL相比CE降低多少倍 |
| 1 | 0.9 | 1 | 0.9 | 0.105 | 0.00026 | 400 |
| 2 | 0.968 | 1 | 0.968 | 0.033 | 0.000008 | 3906 |
| 3 | 0.1 | 0 | 0.9 | 0.105 | 0.00079 | 133 |
| 4 | 0.032 | 0 | 0.968 | 0.033 | 0.000025 | 1302 |
| 5 | 0.1 | 1 | 0.1 | 2.3 | 0.466 | 4.9 |
| 6 | 0.9 | 0 | 0.1 | 2.3 | 1.4 | 1.6 |
- 对于1,2行,它们预测目标的概率非常高,很明显是属于简单样本,我们发现,CE对与它们的Loss计算比较大,而FL给了它们一个非常小的权重。而且 p t p_t pt越大,对应的loss也就越低。
- 对于3,4行,它们是负样本,二者的难易程度表明它俩是简单样本,FL应该对其loss进行缩减。看一下结果,的确FL的值更小, p t p_t pt越大,Loss越小。
- 对于第5行, p t = 0.1 p_t=0.1 pt=0.1,说明它非常难以预测,因此它的Loss很重要(因为要干掉它,所以要给他足够的关注)。我们可以看到,CE达到了2.3,足够respect;但FL只有0.466,是不是有点不尊重它了?其实不然,因为你看前面几行,它们的FL都是0.000xxx,而这里是0.466,相比来说,还是足够respect了
- 对于最后一行,它的 p t = 1 − 0.9 = 0.1 p_t=1-0.9=0.1 pt=1−0.9=0.1,也是难以预测的样本,CE给出的Loss仍然是2.3,FL给出的Loss为1.4
其实看rate那一列就可以了,对于易预测样本(No. 1,2,3,4)它们的rate都是成百上千的;对于难以预测的样本(No. 5,6)它们的rate是个位数。这说明,对于难以预测的样本,FL相比CE给出了足够的关注 。
4.5.10 总结
- Focal Loss允许网络更加关注于训练难以学习的样本;对于容易学习的样本,网络就不怎么关注它们
Q:Focal Loss在实际使用时效果大吗?到底有没有用?
A:FL正常来说是有用的,但需要花费一些时间去调参( γ \gamma γ和 α \alpha α)。如果调参调的不好,可能它并不是很work(效果不如CE和hard negative mining,甚至像YOLO v3原论文中那样出现掉点的情况)。
CE:YOLO v3
hard negative mining:SSD、Faster R-CNN
4.5.11 注意事项
在采用Focal Loss时要注意,训练集的标注GT尽可能要正确,尽量不要有错误的GT。
如果有错误的GT,Focal Loss可能会针对这些错误的GT疯狂学习,导致网络的效果越来越差
标注错误的Object对于网络来说绝对是一个难以学习的样本
Focal Loss易受到噪音的干扰!
4.6 YOLO v1~v3和v3-SPP的grid cell划分以及anchors个数
| 模型 | grid cell个数 | 每个grid cell对应anchor个数 | anchor总数 |
|---|---|---|---|
| YOLO v1 | 7×7 | 2 | 7×7×2=98 |
| YOLO v2 | 13×13 | 5 | 13×13×5=845 |
| YOLO v3 | 三种不同的尺度(13, 26, 52) | 3 | (13×13+26×26+52×52)×3=10647 |
| YOLO v3-SPP | 三种不同的尺度(16, 32, 64) | 3 | (16×16+32×32+64×64)×3=16128 |
参考
- https://www.bilibili.com/video/BV1yi4y1g7ro?spm_id_from=333.999.0.0
- https://github.com/ultralytics/yolov3
- https://blog.csdn.net/qq_37541097/article/details/81214953
- https://zhuanlan.zhihu.com/p/94799295