统计学习导论(六)线性模型选择与正则化——学习笔记
1. 子集选择
1.1 最优子集选择
对 p p p个预测变量的所有可能组合分别使用最小二乘回归进行拟合:对含有一个预测变量的模型,拟合 p p p个模型;对含有两个预测变量的模型,拟合 p ( p − 1 ) / 2 p(p-1)/2 p(p−1)/2个模型……,最后在所有可能模型中选取最优模型。
| 算法1 最优子集选择(p个变量,在 2 p 2^p 2p个模型中选择最优模型) |
|---|
| 1. 记不含预测变量的零模型为 M 0 M_{0} M0,只用于估计各观测的样本均值 |
| 2. 对于 k = 1 , 2 , … … , p k=1,2,……,p k=1,2,……,p:(a)拟合 p ( p − 1 ) / k p(p-1)/k p(p−1)/k个包含k个预测变量的模型; |
| (b)在 p ( p − 1 ) / k p(p-1)/k p(p−1)/k个模型中选择RSS(偏差—logistic)最小或R²最大的作为最优模型,记为 M k M_{k} Mk |
| 3. 根据交叉验证预测误差、 C p ( A I C ) C_{p}(AIC) Cp(AIC)、BIC或者调整R²,从 M 0 , … … , M p M_{0},……,M_{p} M0,……,Mp个模型中选择最优模型 |
简单直观,但是计算效率不高,会出现过拟合以及系数估计方差高的问题。
1.2 逐步选择
1.2.1 向前逐步选择
以一个不包含任何预测变量的零模型为起点,依次往模型中添加变量,直至所有的预测变量都在模型中。(每次只将能提升模型效果max的变量加入模型)
| 算法2 向前逐步选择 |
|---|
| 1. 记不含预测变量的零模型为 M 0 M_{0} M0; |
| 2. 对于 k = 0 , 2 , … … , p − 1 k=0,2,……,p-1 k=0,2,……,p−1:(a)从 p − k p-k p−k个模型中进行选择,每个模型只在 M k M_{k} Mk的基础上增加一个变量; |
| (b)在 p − k p-k p−k个模型中选择RSS(偏差—logistic)最小或R²最大的作为最优模型,记为 M k + 1 M_{k+1} Mk+1 |
| 3. 根据交叉验证预测误差、 C p ( A I C ) C_{p}(AIC) Cp(AIC)、BIC或者调整R²,从 M 0 , … … , M p M_{0},……,M_{p} M0,……,Mp个模型中选择最优模型 |
相比于最优子集选择,运算效率有所提高,但无法保证找到的模型是 2 p 2^p 2p个模型中最优的。
1.2.2 向后逐步选择
| 算法3 向后逐步选择 |
|---|
| 1. 记包含全部p个预测变量的全模型为 M p M_{p} Mp; |
| 2. 对于 k = p , p − 1 , … , 1 k=p,p-1,…,1 k=p,p−1,…,1:(a)从 k k k个模型中进行选择,在模型 M k M_{k} Mk的基础上减少一个变量,则模型只含k-1个变量; |
| (b)在 k k k个模型中选择RSS(偏差—logistic)最小或R²最大的作为最优模型,记为 M k − 1 M_{k-1} Mk−1 |
| 3. 根据交叉验证预测误差、 C p ( A I C ) C_{p}(AIC) Cp(AIC)、BIC或者调整R²,从 M 0 , … … , M p M_{0},……,M_{p} M0,……,Mp个模型中选择最优模型 |
向后选择方法需满足样本量n 大于变量个数p,当n R S S RSS RSS与 R 2 R^2 R2并不适用于对包含不同个数预测变量模型进行模型选择,它们都与训练误差有关,我们希望具有最小的测试误差,训练误差可能是测试误差的一个较差估计。 C p C_{p} Cp值 赤池信息量准则(Akaike information criterion, AIC) 贝叶斯信息准则(Bayesian information criterion, BIC) 调整的 R 2 R^2 R2 为每个可能最优的模型计算验证集误差或者交叉验证误差,选择测试误差估计值最小的模型。 对系数进行约束或加罚的技巧对包含p个预测变量的模型进行拟合,通过压缩系数估计值,显著减少了估计量方差。 岭回归与最小二乘相似: 岭回归估计系数受预测变量尺度变化的影响,所以使用岭回归前,要对预测变量进行标准化,统一尺度: VS 最小二乘回归:综合权衡了误差与方差,随着 λ \lambda λ的增加,岭回归拟合结果的光滑度降低,虽然方差降低,但是偏差在增加。 岭回归的最终模型包含全部p个变量,惩罚项 λ ∑ j = 1 p β j 2 \lambda \sum_{j=1}^{p} \beta_{j}^{2} λ∑j=1pβj2可以将系数往0的方向进行缩减,但是不会把任何一个变量的系数确切地压缩至0。这种设定不影响预测精度,但是当变量个数p非常大时,不便于模型解释。lasso回归克服了岭回归的上述缺点。 当一小部分预测变量是真实有效的而其他预测变量系数非常小或为0,lasso回归效果更好 选择一系列 λ \lambda λ的值,计算每个 λ \lambda λ的交叉验证误差,选择使交叉验证误差最小的参数值; 降维方法:将预测变量进行转换,然后用转换之后的变量拟合最小二乘模型。 M<p 主成分分析(PCA),是一种可以从多个变量中得到低维变量的有效方法。 应用主成分回归时,在构造主成分前要对每个变量进行标准化处理,保证变量在相同的尺度上。 主成分回归能够最大限度地代表预测变量 X 1 , X 2 , … , X P X_{1}, X_{2}, \ldots, X_{P} X1,X2,…,XP的线性组合或方向,这些方向是通过无指导方法得到的,因此响应变量 Y Y Y没有指导主成分的构造过程:无法保证那些能够很好解释预测变量的方向同样也能很好地预测响应变量。 偏最小二乘,是一种有指导的主成分回归替代方法。 偏最小二乘回归在化学统计学领域应用广泛,它的表现没有岭回归与主成分回归好,作为有指导的降维技术,PLS虽然能够减小偏差,但其也可能同时增大方差。 特征数p比观测数n大的数据被称为高维数据。 向前逐步选择、岭回归、lasso、主成分回归等用于拟合并不光滑的最小二乘模型的方法,在高维回归中作用很大,与最小二乘法相比,有效地避免了过拟合问题。 在高维情况下,存在非常极端的共线性问题:模型中的任何一个变量都可以写成其他所有变量的线性组合。我们只能增大可以预测输出变量的变量的系数。 regsubset()函数(leaps库中)通过建立一系列包含给定数目预测变量的最优模型,来实现最优预测变量子集的筛选。最优通过RSS量化,语法与lm()相同,summary()输出模型大小不同的情况下最优的预测变量子集。 向前向后通过设定regsubsets()中的参数method=“forward”/"backward"实现 使用向前,向后逐步选择和最优子集选择得到的最优七变量模型不同。 使用验证集选择模型 使用交叉验证集 使用程序包glmnet来实现岭回归与lasso。使用glmnet()函数时,必须输入一个x矩阵,和一个y向量。 使用pls库中pcr()函数实现主成分回归 在训练集上使用PCR(有问题)1.3 选择最优模型
通常:
1.3.1 C p 、 A I C 、 B I C 、 调 整 的 R 2 C_{p}、AIC、BIC、调整的R^2 Cp、AIC、BIC、调整的R2
采用最小二乘法拟合一个包含d个预测变量的模型,其 C p C_{p} Cp值为:
C p = 1 n ( R S S + 2 d σ ^ 2 ) C_{p}=\frac{1}{n}\left(\mathrm{RSS}+2 d \hat{\sigma}^{2}\right) Cp=n1(RSS+2dσ^2)
其中 σ ^ 2 \hat{\sigma}^{2} σ^2是标准线性回归模型中各个响应变量观测误差的方差 ϵ \epsilon ϵ的估计值,选择具有最低 C p C_{p} Cp值的模型作为最优模型。
A I C = 1 n σ ^ 2 ( R S S + 2 d σ ^ 2 ) \mathrm{AIC}=\frac{1}{n \hat{\sigma}^{2}}\left(\mathrm{RSS}+2 d \hat{\sigma}^{2}\right) AIC=nσ^21(RSS+2dσ^2)
AIC准则适用于许多使用极大似然法进行拟合的模型。若标准线性回归模型的误差项服从高斯分布,极大似然估计和最小二乘估计是等价的。
对于最小二乘模型, C p C_{p} Cp与AIC彼此成比例。
B I C = 1 n σ ^ 2 ( R S S + log ( n ) d σ ^ 2 ) \mathrm{BIC}=\frac{1}{n \hat{\sigma}^{2}}\left(\mathrm{RSS}+\log (n) d \hat{\sigma}^{2}\right) BIC=nσ^21(RSS+log(n)dσ^2)
与 C p C_{p} Cp类似,测试误差较低的模型BIC统计量取值较低,选择具有最低BIC的模型为最优模型。
BIC将 C p C_{p} Cp中的 d σ ^ 2 d \hat{\sigma}^{2} dσ^2替换为 log ( n ) d σ ^ 2 \log (n) d \hat{\sigma}^{2} log(n)dσ^2,n为观测数量,对于任意n>7,logn>2,BIC统计量通常给包含多个变量的模型进行较重的惩罚,与 C p C_{p} Cp相比,得到的模型规模更小。
Adjusted R 2 = 1 − RSS / ( n − d − 1 ) TSS / ( n − 1 ) \text { Adjusted } R^{2}=1-\frac{\operatorname{RSS} /(n-d-1)}{\operatorname{TSS} /(n-1)} Adjusted R2=1−TSS/(n−1)RSS/(n−d−1)
与 C p C_{p} Cp、AIC、BIC不同,调整的 R 2 R^2 R2越大,模型的测试误差越小。
与 R 2 R^2 R2统计量不同,调整的 R 2 R^2 R2对对纳入不必要变量的模型引入了惩罚。1.3.2 验证与交叉验证
与1.3.1的方法相比,优势在于,给出了测试误差的一个直接估计,并对真实的潜在模型有较少的假设,适用范围更广泛。
一倍标准误差准则:
这样在一系列效果近似相同的模型中,总是倾向于选择最简单的模型。2. 压缩估计方法
2.1 岭回归
最小二乘回归,通过最小化函数 RSS = ∑ i = 1 n ( y i − β 0 − ∑ j = 1 p β j x i j ) 2 \operatorname{RSS}=\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} x_{i j}\right)^{2} RSS=∑i=1n(yi−β0−∑j=1pβjxij)2,对 β 0 , β 1 , … , β p \beta_{0}, \beta_{1}, \ldots, \beta_{p} β0,β1,…,βp进行估计。
岭回归系数估计值 β ^ R \hat{β}^{R} β^R,通过最小化下式获得:
∑ i = 1 n ( y i − β 0 − ∑ j = 1 p β j x i j ) 2 + λ ∑ j = 1 p β j 2 = R S S + λ ∑ j = 1 p β j 2 \sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} x_{i j}\right)^{2}+\lambda \sum_{j=1}^{p} \beta_{j}^{2}=\mathrm{RSS}+\lambda \sum_{j=1}^{p} \beta_{j}^{2} i=1∑n(yi−β0−j=1∑pβjxij)2+λj=1∑pβj2=RSS+λj=1∑pβj2
其中, λ ≥ 0 \lambda≥0 λ≥0是一个调节参数,单独确定。控制RSS与惩罚项对回归系数估计的相对影响程度。
与最小二乘相同,岭回归通过最小化RSS寻求较好地拟合数据的估计量。
λ ∑ j = 1 p β j 2 \lambda \sum_{j=1}^{p} \beta_{j}^{2} λ∑j=1pβj2为压缩惩罚项,当 β 0 , β 1 , … , β p \beta_{0}, \beta_{1}, \ldots, \beta_{p} β0,β1,…,βp接近0时较小,因此具有将 β j \beta_{j} βj估计值往0的方向进行压缩的作用。
当 λ = 0 \lambda=0 λ=0,惩罚项不产生作用,岭回归与最小二乘回归结果相同;当 λ → ∞ \lambda→∞ λ→∞,压缩惩罚项的影响力增大,岭回归系数估计值越来越接近0,所以岭回归得到的系数估计 β ^ R \hat{β}^{R} β^R随 λ \lambda λ变化而变化。
若数据矩阵 X X X的列在岭回归前已经进行中心化,均值为0,则截距项估计值为: β ^ 0 = y ˉ = ∑ i = 1 n y i / n \hat{\beta}_{0}=\bar{y}=\sum_{i=1}^{n} y_{i} / n β^0=yˉ=∑i=1nyi/n
x ~ i j = x i j 1 n ∑ i = 1 n ( x i j − x ˉ j ) 2 \tilde{x}_{i j}=\frac{x_{i j}}{\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i j}-\bar{x}_{j}\right)^{2}}} x~ij=n1∑i=1n(xij−xˉj)2xij2.2 lasso回归
lasso的系数 β ^ L \hat{β}^{L} β^L通过最小化下式得到:
∑ i = 1 n ( y i − β 0 − ∑ j = 1 p β j x i j ) 2 + λ ∑ j = 1 p ∣ β j ∣ = RSS + λ ∑ j = 1 p ∣ β j ∣ \sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\sum_{j=1}^{p} \beta_{j} x_{i j}\right)^{2}+\lambda \sum_{j=1}^{p}\left|\beta_{j}\right|=\operatorname{RSS}+\lambda \sum_{j=1}^{p}\left|\beta_{j}\right| i=1∑n(yi−β0−j=1∑pβjxij)2+λj=1∑p∣βj∣=RSS+λj=1∑p∣βj∣
与岭回归的区别在于, β j 2 \beta_{j}^2 βj2替换为 ∣ β j ∣ |\beta_{j}| ∣βj∣。lasso采用 l 1 l_{1} l1惩罚项,而不是 l 2 l_{2} l2惩罚项。系数 β \beta β的 l 1 l_{1} l1范数定义为 ∥ β ∥ 1 = ∑ ∣ β j ∣ \|\beta\|_{1}=\sum\left|\beta_{j}\right| ∥β∥1=∑∣βj∣。当 λ \lambda λ足够大时, l 1 l_{1} l1惩罚项具有将其中某些系数的估计值强制设定为0的作用,从而达到变量选择的目的。
lasso得到了稀疏模型(sparse model)——只包含所有变量一个子集的模型。
当响应变量是很多预测变量的函数并且这些变量系数大致相等,岭回归更出色
但是,对于真实数据集,与响应变量有关的变量个数无法事先知道,因此交叉验证用于决定哪个方法更适合。2.3 选择调节参数 λ \lambda λ
交叉验证和lasso的结合可以正确识别模型的信号变量与噪声变量。3. 降维方法
令 Z 1 , Z 2 , … , Z M Z_{1}, Z_{2}, \ldots, Z_{M} Z1,Z2,…,ZM表示 M M M个原始预测变量的线性组合( M < p M
Z m = ∑ j = 1 p ϕ j m X j Z_{m}=\sum_{j=1}^{p} \phi_{j m} X_{j} Zm=j=1∑pϕjmXj
其中, ϕ 1 m , ϕ 2 m … , ϕ p m \phi_{1 m}, \phi_{2 m} \ldots, \phi_{p m} ϕ1m,ϕ2m…,ϕpm是常数, m = 1 , … , M m=1,…,M m=1,…,M,可以用最小二乘拟合线性回归模型
y i = θ 0 + ∑ m = 1 M θ m z i m + ϵ i , i = 1 , … , n y_{i}=\theta_{0}+\sum_{m=1}^{M} \theta_{m} z_{i m}+\epsilon_{i}, \quad i=1, \ldots, n yi=θ0+m=1∑Mθmzim+ϵi,i=1,…,n
θ 0 , θ 1 , … , θ M \theta_{0},\theta_{1},…,\theta_{M} θ0,θ1,…,θM是回归系数。
降维使估计 p + 1 p+1 p+1个系数变为估计 M + 1 M+1 M+1个系数,问题的维度从 p + 1 p+1 p+1降至 M + 1 M+1 M+13.1 主成分回归
主成分回归(PCR),是指构造钱前 M M M个主成分 Z 1 , Z 2 , … , Z M Z_{1}, Z_{2}, \ldots, Z_{M} Z1,Z2,…,ZM,将这些主成分作为预测变量,用最小二乘拟合线性回归模型:少数的主成分足以解释大部分数据波动以及数据与响应变量之间的关系。它不是特征提取法,主成分都是p个原始变量的线性组合。与岭回归相似。3.2 偏最小二乘(partial least squares, PLS)
与主成分回归相同的是,偏最小二乘也是一种降维手段,将原始变量的线性组合 Z 1 , Z 2 , … , Z M Z_{1}, Z_{2}, \ldots, Z_{M} Z1,Z2,…,ZM作为新的变量集进行最小二乘拟合;
与主成分回归不同的是,偏最小二乘通过有指导的方法进行新特征提取,即利用了响应变量 Y Y Y的信息筛选新变量,试图寻找一个可以同时解释响应变量和预测变量的方向。4. 高维问题
4.1 高维数据
当p>n或p≈n时,简单最小二乘回归线非常光滑,因此导致过拟合。4.2 高维数据的回归
lasso例,page 242(pdf 256)中文书P166
3*. 测试误差随着数据维度(特征或预测变量个数)的增加而增大,除非新增的特征变量与响应变量确实相关。
特别地,3.是分析高维数据的关键问题,被称为维数灾难。
通常,与响应变量真实相关的新增特征将通过降低测试集误差而提高模型的拟合质量;但与响应变量并不相关的新增噪声会降低模型的拟合质量,增大测试集误差。4.3 高维数据分析结果解释
注意:
5. R语言实现
5.1 子集选择方法
5.1.1 最优子集选择
> library(ISLR)
> fix(Hitters)#查看数据集,发现Salary变量存在缺失值
> names(Hitters)
[1] "AtBat" "Hits" "HmRun" "Runs" "RBI" "Walks" "Years" "CAtBat" "CHits" "CHmRun"
[11] "CRuns" "CRBI" "CWalks" "League" "Division" "PutOuts" "Assists" "Errors" "Salary" "NewLeague"
> dim(Hitters)
[1] 322 20
> sum(is.na(Hitters$Salary))#is.na()函数可用于识别有缺失值的观测:该函数返回一个与输入向量等长的向量,TRUE表示输入向量该位置的元素确缺失,FALSE表示非缺失
[1] 59
> #sum()用于计算所有缺失值得个数
> Hitters=na.omit(Hitters)#数据集中有59个运动员的Salary变量值缺失,na.omit()函数可以删除在任何变量上存在缺失值的观测
> dim(Hitters)
[1] 263 20
> sum(is.na(Hitters))
[1] 0
> library(leaps)
> regfit.full=regsubsets(Salary~.,Hitters)
> summary(regfit.full)
Subset selection object
Call: regsubsets.formula(Salary ~ ., Hitters)
19 Variables (and intercept)
Forced in Forced out
AtBat FALSE FALSE
Hits FALSE FALSE
HmRun FALSE FALSE
Runs FALSE FALSE
RBI FALSE FALSE
Walks FALSE FALSE
Years FALSE FALSE
CAtBat FALSE FALSE
CHits FALSE FALSE
CHmRun FALSE FALSE
CRuns FALSE FALSE
CRBI FALSE FALSE
CWalks FALSE FALSE
LeagueN FALSE FALSE
DivisionW FALSE FALSE
PutOuts FALSE FALSE
Assists FALSE FALSE
Errors FALSE FALSE
NewLeagueN FALSE FALSE
1 subsets of each size up to 8
Selection Algorithm: exhaustive
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors
1 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " "
2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " "
3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " " " "*" " " " "
4 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " "*" "*" " " " "
5 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " " " "*" " " " " "*" "*" " " " "
6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " " "*" " " " " "*" "*" " " " "
7 ( 1 ) " " "*" " " " " " " "*" " " "*" "*" "*" " " " " " " " " "*" "*" " " " "
8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " "*" "*" " " "*" " " "*" "*" " " " "
NewLeagueN
1 ( 1 ) " "
2 ( 1 ) " "
3 ( 1 ) " "
4 ( 1 ) " "
5 ( 1 ) " "
6 ( 1 ) " "
7 ( 1 ) " "
8 ( 1 ) " "
> #*表示列对应的变量包含于行对应的模型中。在regsubsets()的默认设置下,输出结果截至最优八变量模型的结果。设置nvmax可以改变预测变量个数,eg.截至最优十九个
> regfit.full=regsubsets(Salary~.,data=Hitters,nvmax=19)
> reg.summary=summary(regfit.full)
> #summary()函数返回了相应模型的R²,RSS,调整的R²,CP及BIC
> names(reg.summary)
[1] "which" "rsq" "rss" "adjr2" "cp" "bic" "outmat" "obj"
> reg.summary$rsq
[1] 0.3214501 0.4252237 0.4514294 0.4754067 0.4908036 0.5087146 0.5141227 0.5285569 0.5346124 0.5404950 0.5426153 0.5436302 0.5444570
[14] 0.5452164 0.5454692 0.5457656 0.5459518 0.5460945 0.5461159
> #同时画出所有模型的RSS、调整的R²,CP及BIC的图像可以辅助确定最终选择哪个模型,type=l选择在R中用实线连接图像上的点
> par(mfrow=c(2,2))
> plot(reg.summary$rss,xlab="Number of Variables",ylab="RSS",type ='l')
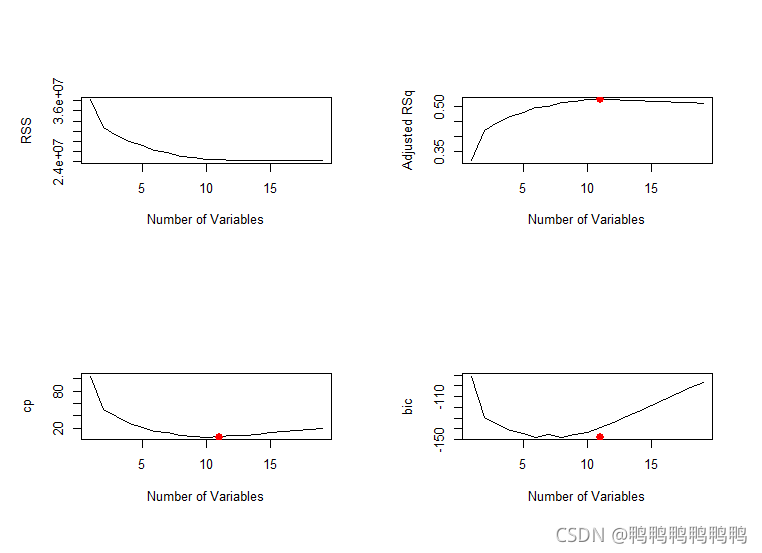
> plot(reg.summary$adjr2,xlab="Number of Variables",ylab="Adjusted RSq",type="l")
> #points()用于将点加在已有图像上,不是作新的图像
> which.max(reg.summary$adjr2)#识别向量中最大值所对应点的位置
[1] 11
> points(11,reg.summary$adjr2[11],col="red",cex=2,pch=20)#用一个红色的点来表示调整后R²最大的模型
> #使用类似的方法做CP,BIC统计指标的图像,结合which.min()标识最小的模型
> plot(reg.summary$cp,xlab="Number of Variables",ylab="cp",type="l")
> which.min(reg.summary$cp)
[1] 10
> points(11,reg.summary$cp[10],col="red",cex=2,pch=20)
> plot(reg.summary$bic,xlab="Number of Variables",ylab="bic",type="l")
> which.min(reg.summary$bic)
[1] 6
> points(11,reg.summary$bic[6],col="red",cex=2,pch=20)
> #reg.subsets()函数内置的plot(),可以输出按照BIC,CP,调整的R²,AIC排序后,包含给定个数预测变量的最优模型所含变量的情况→?plot.regsubsets
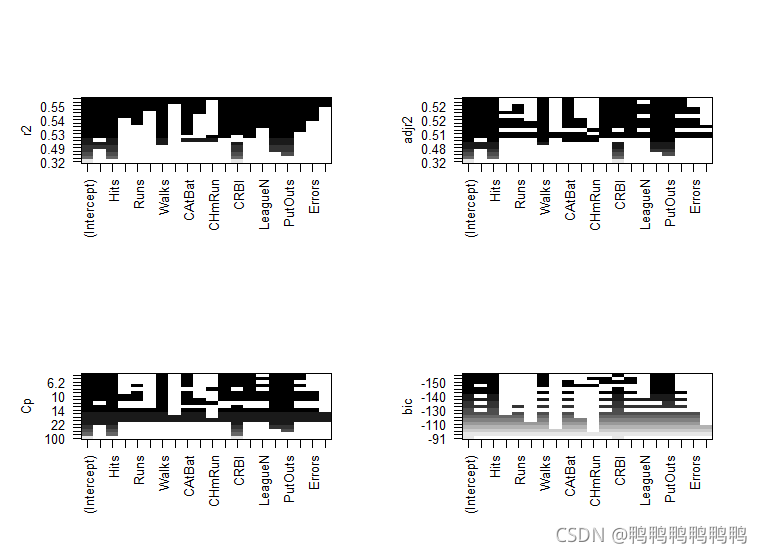
> plot(regfit.full,scale="r2")
> plot(regfit.full,scale="adjr2")
> plot(regfit.full,scale="Cp")
> plot(regfit.full,scale="bic")
> > #图像第一行的黑色方块表示根据相应统计指标选择的最优模型所包含的变量。BIC指标最小的有六个变量,可以使用coef()提取该模型的参数估计值
> coef(regfit.full,6)
(Intercept) AtBat Hits Walks CRBI DivisionW PutOuts
91.5117981 -1.8685892 7.6043976 3.6976468 0.6430169 -122.9515338 0.2643076
5.1.2 向前与向后逐步选择
> regfit.fwd=regsubsets(Salary~.,data = Hitters,nvmax=19,method = "forward")
> summary(regfit.fwd)
Subset selection object
Call: regsubsets.formula(Salary ~ ., data = Hitters, nvmax = 19, method = "forward")
19 Variables (and intercept)
Forced in Forced out
AtBat FALSE FALSE
Hits FALSE FALSE
HmRun FALSE FALSE
Runs FALSE FALSE
RBI FALSE FALSE
Walks FALSE FALSE
Years FALSE FALSE
CAtBat FALSE FALSE
CHits FALSE FALSE
CHmRun FALSE FALSE
CRuns FALSE FALSE
CRBI FALSE FALSE
CWalks FALSE FALSE
LeagueN FALSE FALSE
DivisionW FALSE FALSE
PutOuts FALSE FALSE
Assists FALSE FALSE
Errors FALSE FALSE
NewLeagueN FALSE FALSE
1 subsets of each size up to 19
Selection Algorithm: forward
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors
1 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " "
2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " "
3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " " " "*" " " " "
4 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " " "*" " " " " "*" "*" " " " "
5 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " " " "*" " " " " "*" "*" " " " "
6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " " "*" " " " " "*" "*" " " " "
7 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " " "*" "*" " " "*" "*" " " " "
8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*" "*" "*" " " "*" "*" " " " "
9 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" " " "*" "*" " " " "
10 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" " " "*" "*" "*" " "
11 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" " "
12 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" " "
13 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" "*"
14 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" "*"
15 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
16 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
17 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
NewLeagueN
1 ( 1 ) " "
2 ( 1 ) " "
3 ( 1 ) " "
4 ( 1 ) " "
5 ( 1 ) " "
6 ( 1 ) " "
7 ( 1 ) " "
8 ( 1 ) " "
9 ( 1 ) " "
10 ( 1 ) " "
11 ( 1 ) " "
12 ( 1 ) " "
13 ( 1 ) " "
14 ( 1 ) " "
15 ( 1 ) " "
16 ( 1 ) " "
17 ( 1 ) "*"
18 ( 1 ) "*"
19 ( 1 ) "*"
> regfit.bwd=regsubsets(Salary~.,data = Hitters,nvmax=19,method = "backward")
> summary(regfit.bwd)
Subset selection object
Call: regsubsets.formula(Salary ~ ., data = Hitters, nvmax = 19, method = "backward")
19 Variables (and intercept)
Forced in Forced out
AtBat FALSE FALSE
Hits FALSE FALSE
HmRun FALSE FALSE
Runs FALSE FALSE
RBI FALSE FALSE
Walks FALSE FALSE
Years FALSE FALSE
CAtBat FALSE FALSE
CHits FALSE FALSE
CHmRun FALSE FALSE
CRuns FALSE FALSE
CRBI FALSE FALSE
CWalks FALSE FALSE
LeagueN FALSE FALSE
DivisionW FALSE FALSE
PutOuts FALSE FALSE
Assists FALSE FALSE
Errors FALSE FALSE
NewLeagueN FALSE FALSE
1 subsets of each size up to 19
Selection Algorithm: backward
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors
1 ( 1 ) " " " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " " " "
2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " " " "
3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " "*" " " " " " " " " "*" " " " "
4 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " "*" " " " " " " " " "*" " " " "
5 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*" " " " " " " " " "*" " " " "
6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*" " " " " " " "*" "*" " " " "
7 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*" " " "*" " " "*" "*" " " " "
8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*" "*" "*" " " "*" "*" " " " "
9 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" " " "*" "*" " " " "
10 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" " " "*" "*" "*" " "
11 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" " "
12 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" " "
13 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" "*"
14 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" " " " " "*" "*" "*" "*" "*" "*" "*" "*"
15 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
16 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
17 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*"
19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
NewLeagueN
1 ( 1 ) " "
2 ( 1 ) " "
3 ( 1 ) " "
4 ( 1 ) " "
5 ( 1 ) " "
6 ( 1 ) " "
7 ( 1 ) " "
8 ( 1 ) " "
9 ( 1 ) " "
10 ( 1 ) " "
11 ( 1 ) " "
12 ( 1 ) " "
13 ( 1 ) " "
14 ( 1 ) " "
15 ( 1 ) " "
16 ( 1 ) " "
17 ( 1 ) "*"
18 ( 1 ) "*"
19 ( 1 ) "*"
> coef(regfit.full,7)
(Intercept) Hits Walks CAtBat CHits CHmRun DivisionW PutOuts
79.4509472 1.2833513 3.2274264 -0.3752350 1.4957073 1.4420538 -129.9866432 0.2366813
> coef(regfit.fwd,7)
(Intercept) AtBat Hits Walks CRBI CWalks DivisionW PutOuts
109.7873062 -1.9588851 7.4498772 4.9131401 0.8537622 -0.3053070 -127.1223928 0.2533404
> coef(regfit.bwd,7)
(Intercept) AtBat Hits Walks CRuns CWalks DivisionW PutOuts
105.6487488 -1.9762838 6.7574914 6.0558691 1.1293095 -0.7163346 -116.1692169 0.3028847
5.1.3 使用验证集和交叉验证选择模型
> library(ISLR)
> Hitters=na.omit(Hitters)
> set.seed(1)
> #定义一个随机向量train完成数据集的拆分,train中TRUE在训练集中,FALSE在测试集中
> train=sample(c(TRUE,FALSE),nrow(Hitters),rep=TRUE)
> #!将TRUE与FALSE进行转化
> test=(!train)
> #用regsubsets()在训练集上完成最优子集选择
> library(leaps)
> regfit.best=regsubsets(Salary~.,data=Hitters[train,],nvmax=19)
> #data=Hitters[train,]直接调用了数据的训练集
> #计算在不同模型大小下,最优模型的验证集误差
> #首先,使用测试数据生成一个回归设计矩阵,model.matrix()在回归程序包中用于生成回归设计矩阵“X”
> test.mat=model.matrix(Salary~.,data=Hitters[test,])
> #使用循环语句进行参数估计和预测
> val.errors=rep(NA,19)
> for (i in 1:19) {
+ coefi=coef(regfit.best,id=i)
+ pred=test.mat[,names(coefi)]%*%coefi
+ val.errors[i]=mean((Hitters$Salary[test]-pred)^2)
+ }
> #第i次循环,从regfit.best中提取模型大小为i时最优模型的参数估计结果,并将提取的参数估计向量乘以生成的回归设计矩阵,计算出预测值和测试集的MSE
> val.errors
[1] 164377.3 144405.5 152175.7 145198.4 137902.1 139175.7 126849.0 136191.4 132889.6 135434.9 136963.3 140694.9 140690.9 141951.2
[15] 141508.2 142164.4 141767.4 142339.6 142238.2
> which.min(val.errors)
[1] 7
> coef(regfit.best,7)
(Intercept) AtBat Hits Walks CRuns CWalks DivisionW PutOuts
67.1085369 -2.1462987 7.0149547 8.0716640 1.2425113 -0.8337844 -118.4364998 0.2526925
> #regsubsets()函数没有predict()命令,根据上述步骤,编写一个预测函数
> predict.regsubsets=function(object,newdata,id,...){
+ form=as.formula(object$call[[2]])
+ mat=model.matrix(form,newdata)
+ coefi=coef(object,id=id)
+ xvars=names(coefi)
+ mat[,xvars]%*%coefi
+ }
> #对整个数据集使用最优子集选择,选出最优的十变量模型。基于整个数据集建立的最优十变量模型可能不同于训练集上的对应模型:结果确实不同
> regfit.best=regsubsets(Salary~.,data = Hitters,nvmax = 19)
> coef(regfit.best,7)
(Intercept) Hits Walks CAtBat CHits CHmRun DivisionW PutOuts
79.4509472 1.2833513 3.2274264 -0.3752350 1.4957073 1.4420538 -129.9866432 0.2366813
> #交叉验证:1.定义一个向量将数据集中的每个观测归为k折中的某一折;2.定义一个存储计算结果的矩阵
> k=10
> set.seed(1)
> folds=sample(1:k,nrow(Hitters),replace = TRUE)
> cv.errors=matrix(NA,k,19,dimnames = list(NULL,paste(1:19)))
> #用过循环语句实现交叉验证,第j折,数据集中对用于folds向量中等于j的元素归于测试集,其他元素归于训练集
> #对于不同大小模型,给出基于测试集的预测值,计算相应的测试误差,并存储在矩阵cv.errors相应位置
> for (j in 1:k) {
+ best.fit=regsubsets(Salary~.,data = Hitters[folds!=j,],nvmax=19)
+ for (i in 1:19) {
+ pred=predict(best.fit,Hitters[folds==j,],id=i)
+ cv.errors[j,i]=mean((Hitters$Salary[folds==j]-pred)^2)
+ }
+ }
> #得到10x19的矩阵,矩阵(i,j)元素对应于最优j变量模型第i折交叉验证的测试MSE
> #用apply()求矩阵列平均,得到一个列向量,第j个元素表示j变量模型的交叉验证误差
> mean.cv.errors=apply(cv.errors,2,mean)
> mean.cv.errors
1 2 3 4 5 6 7 8 9 10 11 12 13 14
149821.1 130922.0 139127.0 131028.8 131050.2 119538.6 124286.1 113580.0 115556.5 112216.7 113251.2 115755.9 117820.8 119481.2
15 16 17 18 19
120121.6 120074.3 120084.8 120085.8 120403.5
> par(mfrow=c(1,1))
> plot(mean.cv.errors,type='b')
> which.min(mean.cv.errors)
10
> #交叉验证选择了十变量模型。接下来对整个数据集进行最优子集选择,获得十一变量模型的参数估计结果
> regfit.best=regsubsets(Salary~.,data = Hitters,nvmax = 19)
> coef(regfit.best,10)
(Intercept) AtBat Hits Walks CAtBat CRuns CRBI CWalks DivisionW PutOuts
162.5354420 -2.1686501 6.9180175 5.7732246 -0.1300798 1.4082490 0.7743122 -0.8308264 -112.3800575 0.2973726
Assists
0.2831680
5.2 岭回归和lasso(有点问题)
#使用glmnet()函数必须输入矩阵x和向量y
x=model.matrix(Salary~.,Hitters)[,-1]
y=Hitters$Salary
#model.matrix()对于构造回归设计矩阵x十分有用,该函数不仅能生成一个与19个预测变量相对应的矩阵,还能自动将定性变量转化为哑变量
#glmnet()只能处理数值型输入变量
5.2.1 岭回归
> library(glmnet)
> grid=10^seq(10,-2,length=100)
> ridge.mod=glmnet(x,y,alpha = 0,lambda = grid)
> #alpha=0,拟合岭回归模型;alpha=1,拟合lasso模型
> #默认设置下,lambda的值自动选择;所有变量都进行了标准化,消除了变量尺度上的差别,用standardize=FALSE关闭
> dim(coef(ridge.mod))
[1] 20 100
> #系数向量存储在20x100的矩阵中。一个lambda对应一个岭回归系数向量,用coef(提取存储)
> #使用l2范数,较大lambda所得系数估计值远小于较小lambda所得
> ridge.mod$lambda[50]
[1] 11497.57
> coef(ridge.mod)[,50]
(Intercept) AtBat Hits HmRun
407.356050200 0.036957182 0.138180344 0.524629976
Runs RBI Walks Years
0.230701523 0.239841459 0.289618741 1.107702929
CAtBat CHits CHmRun CRuns
0.003131815 0.011653637 0.087545670 0.023379882
CRBI CWalks LeagueN DivisionW
0.024138320 0.025015421 0.085028114 -6.215440973
PutOuts Assists Errors NewLeagueN
0.016482577 0.002612988 -0.020502690 0.301433531
> sqrt(sum(coef(ridge.mod)[-1,50]^2))
[1] 6.360612
> #对比
> ridge.mod$lambda[60]
[1] 705.4802
> coef(ridge.mod)[,60]
(Intercept) AtBat Hits HmRun
54.32519950 0.11211115 0.65622409 1.17980910
Runs RBI Walks Years
0.93769713 0.84718546 1.31987948 2.59640425
CAtBat CHits CHmRun CRuns
0.01083413 0.04674557 0.33777318 0.09355528
CRBI CWalks LeagueN DivisionW
0.09780402 0.07189612 13.68370191 -54.65877750
PutOuts Assists Errors NewLeagueN
0.11852289 0.01606037 -0.70358655 8.61181213
> sqrt(sum(coef(ridge.mod)[-1,60]^2))
[1] 57.11001
> #使用predict()完成多种任务
> predict(ridge.mod,s=50,type="coefficients")[1:20,]
(Intercept) AtBat Hits HmRun
4.876610e+01 -3.580999e-01 1.969359e+00 -1.278248e+00
Runs RBI Walks Years
1.145892e+00 8.038292e-01 2.716186e+00 -6.218319e+00
CAtBat CHits CHmRun CRuns
5.447837e-03 1.064895e-01 6.244860e-01 2.214985e-01
CRBI CWalks LeagueN DivisionW
2.186914e-01 -1.500245e-01 4.592589e+01 -1.182011e+02
PutOuts Assists Errors NewLeagueN
2.502322e-01 1.215665e-01 -3.278600e+00 -9.496680e+00
> # 第二种分割数据集的方法:随机生成1到n之间的数字子集,将这个子集作为训练集中观测的索引
> # 第二种分割数据集的方法:随机生成1到n之间的数字子集,将这个子集作为训练集中观测的索引
> set.seed(1)
> train=sample(1:nrow(x),nrow(x)/2)
> test=(-train)
> y.test=y[test]
> #基于训练集建立岭回归模型,计算lambda=4时测试集的MSE;
> #predict()中,type改为newx参数,获得测试集上的预测值
> ridge.mod=glmnet(x[train,],y[train],alpha = 0,lambda = grid,thresh = 1e-12)
> ridge.pred=predict(ridge.mod,s=4,newx = x[test,])
> mean((ridge.pred-y.test)^2)
[1] 147072
> #若拟合了只含有截距项的模型,那么模型对测试集中的每个观测给出的预测值为训练集数据的均值
> mean(mean(y[train]-y.test)^2)
[1] 51.77228
Warning message:
In y[train] - y.test :
longer object length is not a multiple of shorter object length
> #可以通过使用一个非常大的lambda值拟合岭回归模型以获得同样的MSE
> ridge.pred=predict(ridge.mod,s=1e10,newx = x[test,])
> mean((ridge.pred-y.test)^2)
[1] 224669.8
> #使用lambda=4拟合的岭回归模型的测试MSE远小于只含有截距项模型的测试MSE
> #下面检验lambda=4拟合的岭回归模型是否优于最小二乘回归模型(lambda=0)
> ridge.pred=predict(ridge.mod,s=0,newx = x[test,],exact = T,x=model.matrix(Salary~.,Hitters[,-1]),y=Hitters$Salary)# exact = T,否则predict()对lambda进行插值
> mean((ridge.pred-y.test)^2)
[1] 102785.2
> lm(y~x,subset = train)
Call:
lm(formula = y ~ x, subset = train)
Coefficients:
(Intercept) x(Intercept) xHits xHmRun xRuns xRBI xWalks xYears xCAtBat
254.3837 NA -2.6868 5.9205 1.7004 1.0196 3.4529 -15.3248 -0.6832
xCHits xCHmRun xCRuns xCRBI xCWalks xLeagueN xDivisionW xPutOuts xAssists
3.3262 3.4183 -0.9997 -0.6465 0.3844 122.5783 -144.4460 0.1948 0.6640
xErrors xNewLeagueN
-4.9417 -73.0425
> predict(ridge.mod,s=0,exact = T,type = "coefficients",x=model.matrix(Salary~.,Hitters[,-1]),y=Hitters$Salary)[1:20,]
(Intercept) (Intercept) Hits HmRun Runs RBI Walks Years CAtBat CHits
67.9256686 0.0000000 2.1885266 4.0522660 -1.9910923 -1.9792873 4.6600391 2.8155719 -0.3429604 0.7819921
CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
-0.1370921 1.0535055 0.8345079 -0.5184468 86.3672996 -129.6155455 0.2552423 0.2992790 -5.0405285 -48.7710421
#一般,拟合最小二乘模型,用lm(),结果更实用
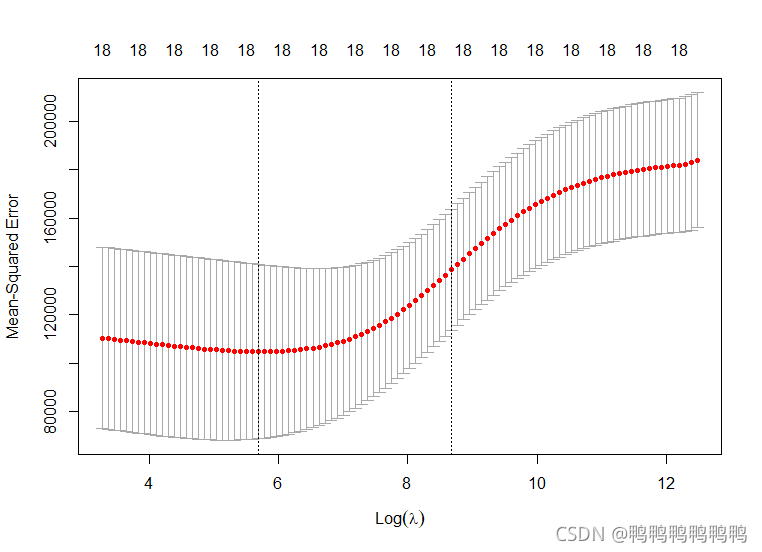
> #建模时。使用交叉验证选择调节参数lambda更好。这里使用cv.glmnet()这个内置交叉验证函数选择lambda。默认10折
> set.seed(1)
> cv.out=cv.glmnet(x[train,],y[train],alpha=0)
> plot(cv.out)
> bestlam=cv.out$lambda.min
> bestlam
[1] 297.1145
> ridge.pred=predict(ridge.mod,s=bestlam,newx = x[test,])
> mean((ridge.pred-y.test)^2)
[1] 140260.9
> #使用交叉验证所得lambda重新拟合岭回归模型
> out=glmnet(x,y,alpha = 0)
> predict(out,type="coefficients",s=bestlam)[1:20,]
(Intercept) (Intercept) Hits HmRun Runs RBI Walks Years CAtBat CHits
21.60060248 0.00000000 0.95542510 0.57042390 1.16193675 0.93964547 1.70696755 1.06457575 0.01144139 0.05933452
CHmRun CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
0.41458597 0.11808610 0.12462703 0.04750174 22.72522243 -81.67311884 0.17340274 0.03860573 -1.36467347 9.03529456
>
> #没有变量的筛选
5.2.2 lasso
#lasso模型
lasso.mod=glmnet(x[train,],y[train],alpha = 1,lambda = grid)
plot(lasso.mod)
#随调节参数不同,预测变量系数会变为0
#使用交叉验证,并计算相应测试误差
set.seed(1)
cv.out=cv.glmnet(x[train,],y[train],alpha=1)
plot(cv.out)
bestlam=cv.out$lambda.min
bestlam
lasso.pre=predict(lasso.mod,s=bestlam,newx = x[test,])
mean((lasso.pre-y.test)^2)
out=glmnet(x,y,alpha = 1,lambda = grid)
lasso.coef=predict(out,type="coefficients",s=bestlam)[1:20,]
lasso.coe
5.3 PCR和PLS回归
5.3.1 主成分回归
> library(pls)
> set.seed(2)
> pcr.fit=pcr(Salary~.,data=Hitters,scale=TRUE,validation="CV")
> #scale=TRUE,生成主成分之前标准化每个预测变量
> #validation="CV",使用10折交叉验证计算每个可能的主成分个数M对应的交叉验证误差
> summary(pcr.fit)
Data: X dimension: 263 19
Y dimension: 263 1
Fit method: svdpc
Number of components considered: 19
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps
CV 452 351.9 353.2 355.0 352.8 348.4
adjCV 452 351.6 352.7 354.4 352.1 347.6
6 comps 7 comps 8 comps 9 comps 10 comps 11 comps
CV 343.6 345.5 347.7 349.6 351.4 352.1
adjCV 342.7 344.7 346.7 348.5 350.1 350.7
12 comps 13 comps 14 comps 15 comps 16 comps
CV 353.5 358.2 349.7 349.4 339.9
adjCV 352.0 356.5 348.0 347.7 338.2
17 comps 18 comps 19 comps
CV 341.6 339.2 339.6
adjCV 339.7 337.2 337.6
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
X 38.31 60.16 70.84 79.03 84.29 88.63
Salary 40.63 41.58 42.17 43.22 44.90 46.48
7 comps 8 comps 9 comps 10 comps 11 comps 12 comps
X 92.26 94.96 96.28 97.26 97.98 98.65
Salary 46.69 46.75 46.86 47.76 47.82 47.85
13 comps 14 comps 15 comps 16 comps 17 comps
X 99.15 99.47 99.75 99.89 99.97
Salary 48.10 50.40 50.55 53.01 53.85
18 comps 19 comps
X 99.99 100.00
Salary 54.61 54.61
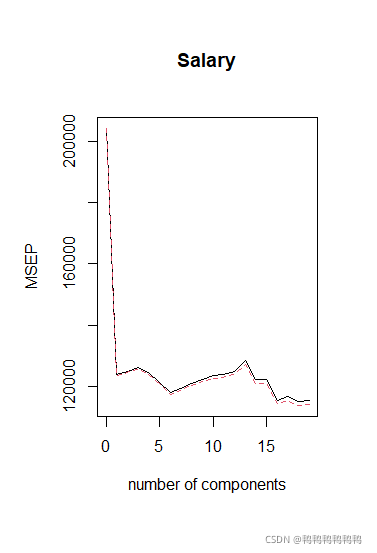
> #M的取值从0开始,pcr()给出的是均方根误差,常用的MSE等于其平方
> > validationplot(pcr.fit,val.type="MSEP")
> validationplot(pcr.fit,val.type="MSEP")
> train=sample(c(TRUE,FALSE),nrow(Hitters),rep=TRUE)
> test=(!train)
> set.seed(1)
> pcr.fit=pcr(Salary~.,data=Hitters[train,],scale=TRUE,validation="CV")
> validationplot(pcr.fit,val.type="MSEP")
5.3.2 偏最小二乘回归