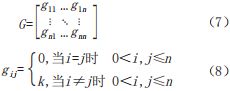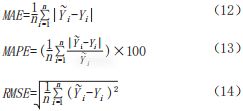lstm中look_back的大小选择_基于时空关联度加权的LSTM短时交通速度预测
作 者 信 息
刘易诗1,关雪峰1,2,吴华意1,2,曹 军1,张 娜1
(1. 武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079;2. 地球空间信息技术协同创新中心,湖北 武汉 430079)
“【摘要】提出一种基于时空关联度加权的长短期记忆网络(Long Short-Term Memory,LSTM)短时交通速度预测模型。该模型结合综合动态时间规整(Summation Dynamic Time Warping,SDTW)和拓扑邻接关系设计了一种路段速度序列之间时空关联程度的度量方法,然后基于该度量值对路段速度历史观测值进行加权,进而使用LSTM从加权观测序列中提取路段速度的时空变化特征,实现对短时交通速度的预测。实验表明,交通速度预测模型预测结果相比传统的ARIMA模型、SVR模型以及LSTM模型均有提升,实现了更高精度的速度预测。
【关键词】交通速度预测;时空关联度;动态时间规整;深度学习;长短期记忆网络
【中图分类号】TP311.12 【文献标识码】A 【文章编号】1672-1586(2020)01-0041-07
”引文格式:刘易诗,关雪峰,吴华意,等. 基于时空关联度加权的LSTM短时交通速度预测[J].地理信息世界,2020,27(1):41-47.
正文
0 引 言
为了解决道路拥堵、事故频发等交通问题,随着车载GPS的普及和交通传感器精度的提高,交通速度(指路段车辆通行速度)作为反映道路交通状态的核心要素,逐渐成为当前交通预测的重点内容之一。由于车辆通行速度随时间和路段不同而波动,如何准确地挖掘交通速度在时间和空间上的特点,成为交通速度预测的关键。
传统基于数据驱动的交通预测方法主要分为两类:基于统计分析的预测方法和一般机器学习方法。统计分析的预测方法如卡尔曼滤波(Kalman Filtering,KF)、自回归滑动平均法(Auto-Regressive Integrated Moving Average,ARIMA)等,比较依赖先验知识,不能很好地挖掘出交通数据本身的信息;一般机器学习方法如k最邻近回归(k-Nearest Neighbors,KNN)、支持向量回归(Support Vector Regression,SVR),虽然信息挖掘能力有所加强,但结构层次单一,缺乏深层特征提取能力。由于深度学习方法具有获取深层特征的能力,许多深度学习模型开始被应用到交通速度预测中。如文献[7]提出了一种时间序列模型和人工神经网络相结合的方法(Time Series-Artificial Neural Network,TS-ANN)分别对实时速度数据和历史速度数据建模预测;文献[8]根据路段平均速度的时空分布特性,设计了基于堆叠自编码器(Stacked Auto-Encoder, SAE)的短时平均速度预测模型;文献[9]结合受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)与循环神经网络(Recurrent Neural Network,RNN)针对宁波的出租车数据进行了预测;文献[10]构建道路的速度-时间矩阵,转化为图像输入到卷积神经网络(Convolutional Neural Network,CNN)中进行特征学习;文献[11]使用微波探测器数据,通过长短期记忆神经网络(Long Short-Term Memory Neural Network,LSTM-NN)来学习交通速度序列的长时序依赖特征;为了获取交通数据在时间上的反向依赖特征,文献[12]使用了双向LSTM(Bi-directional LSTM),实现了大范围高速公路的交通速度预测;文献[13]将路网速度分布图转换成时序灰度影像,结合CNN与LSTM模型进行速度预测。上述这些模型中,CNN能够提取隐含的空间特征,LSTM可以较好地学习长时序规律。
然而,上述研究都没有很好地将时间特征、空间特征进行关联、量化来进行交通速度预测。路段交通速度的空间特征通常用空间邻接关系或图结构表示,时间特征则可以进一步分为两种,路段自身的历史依赖特征以及路段间速度变化在时间上的相似特征。以交通拥堵为例,某个路段出现拥堵现象时,其周围路段也可能会出现相应的滞缓现象,拥堵消失时,邻接路段的车速也会逐渐增加,这两者间的变化模式存在一定的相似性和滞后性。这种速度序列的关联信息,在空间上表现为路段的拓扑邻接关系,在时间上表现为速度变化的相似性关联,共同对交通速度变化产生了至关重要的影响。为了完整体现这种关联信息,我们需要将空间特征和时间特征综合起来考虑,并提供一种量化方法来区分不同关联信息的重要程度,以提升交通速度预测的效果。
为了将关联信息的时空特征输入到模型之中,本文首先设计了一种时空关联度,从时间与空间两个维度量化速度序列之间的关联程度,并将它通过加权的方式对速度序列进行处理。在此基础上,本文提出了一种基于时空关联度加权的LSTM模型(Spatio-Temporal Correlation Long Short-Term Memory,STC-LSTM)用于交通速度预测。模型首先通过综合动态时间规整(Summation Dynamic Time Warping,SDTW)定义了一种时间关联度;然后将它与路段邻接关系相结合,形成了时空关联度,用来综合描述路段间关联程度的时空特征;最后将这种时空关联度作为权重,结合LSTM进行交通速度预测。
1 基于SDTW的时间关联度
时间关联度是用于测定两个给定的速度序列变化曲线之间接近程度的大小度量,本质上是一种相似性度量。而在时间序列相似性度量中,常用的距离函数主要有欧氏距离(Euclidean Distance,ED)、马氏距离(Mahalanobis Distance,MD)、余弦距离(Cosine Distance,CD)等。对于采样间隔一致、长度相同的单变量序列,一般使用欧氏距离作为相似性度量。给定两个速度时间序列X={x1,x2,⋯,xn},Y={y1,y2,⋯,yn},X 和Y为向量,则两者之间的距离DED(X,Y)为:
常用的时序数据相似性距离度量方法有基于ED的离散傅里叶变换(Discrete Fourier Transform,DFT)、基于ED的离散小波变换(Discrete Wavelet Transform,DWT)、动态时间规整(Dynamic Time Warping,DTW)。离散傅里叶变换和离散小波变换都是在频域上对序列信号进行分解,计算不同成分之间的距离,可以起到降噪除杂和分类比较的作用;动态时间规整通过考虑数值上的相似性来对时间尺度进行规整,可以有效地解决时间轴上的偏移、尺度伸缩等问题。由于交通流由分散的车辆组成,其速度变化是通过传递的方式产生,而传递过程需要时间,因此路段间的速度变化影响有一定的滞后特点,相似序列存在偏移现象,考虑到这一点,我们选择使用动态时间规整方法。然而,由于动态时间规整解决时间轴偏移时只考虑了数值大小的特征,无法有效地解决序列在数值轴上的偏移。这会导致进行规整时,一个序列中的某一点映射到另一个序列中的大部分区域的情况,错误计算相似性距离,引起“奇异点问题”。为了解决奇异点问题,需要在动态时间规整的基础上,引入时间维度上的梯度特征,从而减少某一点映射到连续区域的情况,其中比较有效的方法是SDTW。
SDTW首先定义包含数值特征和梯度特征的特征值Fs(x(i))为:
式中,x(i)表示序列X ={x1,x2,…,x n}中的第i个值,max(|∆x|)表示序列X中x(i)-x(i-1)的最大值,代表速度值的最大梯度,这里用相邻点的差分来表示某点的梯度,如用x(i)-x(i-1)表示x(i)的梯度。max(|∆x|)的作用是将各梯度的大小约束在[-1,1]之间,从而以比率的形式将梯度信息融入到特征中。数值特征的比率为1,大于梯度特征的比率,在构建特征时起到了更大作用,而梯度信息起辅助作用。因此,特征Fs对数值上较小的偏差不会过于敏感。结合公式(1),我们可以得到序列X中第i个值到序列Y中第j个值的局部距离d(i,j)为:
![]()
由n×n个局部距离d可以构成距离矩阵D。由此,在边界条件、连续性、单调性三者约束下,我们可以得到序列X和序列Y的规整距离SDTW(x,y)为:
式中,r(i,j)为距离矩阵D中从(0,0)到(i,j)路径上局部距离的累计距离。根据连续性和单调性的约束条件,要到达点只可能从(i-1,j-1)、(i-1,j)或者(i,j-1)出发,min{r(i-1,j-1),r(i-1,j),r(i,j-1)}表示选择三点中累计距离最小的点作为出发点。根据上式,可以算出任意两个路段速度序列之间的相似性距离,构成SDTW距离矩阵。
定义两个路段速度序列XY之间的时间关联度T为:
式中,max(SDTW)为SDTW距离矩阵的最大值。经过归一化后,时间关联度T的范围为[0,1],每个路段与自身的时间关联度为1,两个SDTW距离最远的路段时间关联度为0。两个路段间速度序列的相似性越低,他们的SDTW距离越大,时间关联度越小;相似性越大,SDTW距离越小,时间关联度越大。
2 结合空间邻接关系的时空关联度
考虑到路段交通流向,城市交通路网一般抽象为有向图,但与普通的有向图不同,对于一阶邻接关系而言,上游和下游之间交通状态的影响是双向的。当路段通畅时,影响主要从上游传递到下游路段;当路段拥堵时,下游路段的交通将会影响上游路段的交通状态。因此我们可以得到路网的一阶邻接矩阵S:
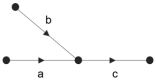
但路网间的交通流关系不仅仅局限于一阶邻接关系。以图1为例,路段a与路段b虽然相邻,但它们不为上下游关系,交通流从路段a和b流向下游路段c,当路段a交通流量增加,必然引起路段c的流量增大,产生交通滞缓,而路段c的滞缓现象也会影响上游路段b,使路段b的车辆速度也相应减慢。路段a与路段b之间的交通流并没有直接联系,它们之间的影响通过路段c间接产生,此时视它们为二阶邻接关系。
图1 路段交通状态影响
Fig.1 Inflfl uences of road traffiffiffi c statuses
二阶邻接关系可以描述为一阶邻接矩阵的一阶邻接,以此类推,迭代下去,我们可以获得路段的k阶邻接关系。在此基础上,定义包含n条路段的整个路网的邻接矩阵G为:
式中,i和j表示路网中的任意两个路段,k表示路段i和不同于i的路段j之间邻接关系的阶数,两个路段邻接关系越近,g越小,邻接关系越远,g越大。
在空间邻接关系和时间关联度的基础上,我们定义两个路段之间的时空关联度wij为:
![]()
式中,采用1/(g+1)的形式,使取值范围在(0,1]之间,一方面是为了让分式有意义,分母大于0;另一方面是为了保证时空关联度与路段间的关联程度成正相关。而使用自然常数作为底数的取幂形式,能将时空关联度的时间特征和空间特征在纵轴上进行拉升,扩大差异,增强时空特征的表达,这有利于下一步加权。最终可以得到所有路段之间的时空关联度矩阵Wx,时空关联度w越大,路段的速度时序数据关联度就越大。
3 基于时空关联度加权的LSTM模型
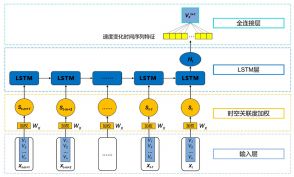
本文提出了一种基于时空关联度加权的长短期记忆网络模型(STC-LSTM),包含一个时空关联度加权部分、一个LSTM层和一个全连接层。具体结构如图2所示。
图2 基于时空关联度加权的LSTM模型
Fig.2 The weighted LSTM model based on spatio-temporal correlation
模型的输入为1~n这n条路段t时刻之前m个时段的历史速度数据,模型的输出结果为预测路段x在t+1时刻的速度值![]() 。为了提高预测精度,模型将时间特征和空间特征融合到权重矩阵中,通过对输入速度加权的方式进行预测。这样把路段间速度变化的关联信息保留了下来,并进一步强调了与预测路段时空关联程度更紧密的路段速度序列,增强了对于路段空间邻接关系和速度变化相似性特征的学习能力。
。为了提高预测精度,模型将时间特征和空间特征融合到权重矩阵中,通过对输入速度加权的方式进行预测。这样把路段间速度变化的关联信息保留了下来,并进一步强调了与预测路段时空关联程度更紧密的路段速度序列,增强了对于路段空间邻接关系和速度变化相似性特征的学习能力。
图中权重矩阵Wx即为上文中的时空关联度矩阵,输入路段数量为n时,矩阵大小为n×n,代表的是各个路段速度序列中速度值的权重,分别与速度序列中的各速度值相乘后求和,这就是时空联度矩阵Wx加权的过程。输入的历史速度数据通过时空关联度矩阵Wx加权,可以得到m个时段的加权速度序列,各加权速度序列S={st-m+1, st-m+2,…,st}。
![]()
式中,wxi为预测路段x与当前路段i的时空关联度,vi为i时刻的速度值。由时空关联度公式可知,待预测路段与其自身的时空关联度一定最大,这保证了加权速度序列大小与关联程度的正相关性。输入数据作为预测模型特征提取的对象,其处理方式会直接影响到特征的选取和预测结果精度,这种加权方式通过改变预测输入的速度值来体现速度序列间关联程度的不同,强调了与预测路段时空关联程度更紧密的路段速度序列。
之后这t个加权速度序列输入到各LSTM单元中进行预测。LSTM层输出的隐状态Ht经过一个全连接层,通过权重矩阵W2和偏置b2就可以计算得到最后的预测速度![]() ,激活函数为Tanh。
,激活函数为Tanh。
![]()
4 实验及分析
4.1 实验数据与模型参数
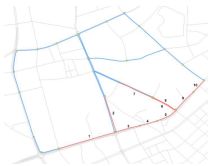
本文实验数据为武汉市2014年6月份30 d内24 h共2 330辆出租车的轨迹数据,其文本字段包括出租车ID、采样时间、经纬度、瞬时速度、行驶方向等,采样频率大概在40 s左右,共9 100万条轨迹记录。首先对轨迹数据进行了异常点清洗、分割和路网匹配等预处理工作,然后筛选出轨迹点覆盖相对较多的路段构成路网子区域来作为研究区域,该区域共有34个路段,如图3所示(蓝色和红色路段)。
图3 预测区域路网结构
Fig.3 The road network structure of study area
从研究区域中,我们选择编号1、2、3、4、5、6、7、8、9、10这10条路段(红色路段)作为预测路段,研究区域中的34个路段作为输入路段,当作预测路段的关联序列信息,与预测路段一起输入到模型中进行预测。
路段的交通速度是道路交通流的平均行驶速度,因此我们需要对瞬时速度进行处理。根据轨迹数据的采样频率和实际分布,我们采用20 min作为时间间隔,则每个路段的速度序列长度为3×24×30=2 160。按照路段和时段划分所有轨迹点后,计算每个路段在每个时间段内所有轨迹点瞬时速度的均值,作为路段速度观测值。
实验的预测任务为用前12个时间段(一个时间段长为20 min)的输入路段的速度历史数据预测下一个时间段的预测路段的速度。数据样本中的80%作为训练数据集,20%作为测试数据集,对于每条路段,即前1 728个速度值为训练数据,后432个速度值为测试数据。模型输入的三维张量![]() ,N_S为输入路段的速度历史数据量1 728,N_T为历史时段数目12,N_R为输入路段数34。
,N_S为输入路段的速度历史数据量1 728,N_T为历史时段数目12,N_R为输入路段数34。
实验采用随机梯度下降法(Stochastic Gradient Descent,SGD)作为模型的优化器,其学习率和衰减值分别设置为0.001和![]() ,损失函数使用均方误差(Mean Squared Error,MSE)。训练时,Batch_size设置为128,epochs设置为500。LSTM神经元个数初始化为40,在输出的全连接层中,神经元个数为1,激活函数选择tanh,参数有41个,总参数为7 360个。
,损失函数使用均方误差(Mean Squared Error,MSE)。训练时,Batch_size设置为128,epochs设置为500。LSTM神经元个数初始化为40,在输出的全连接层中,神经元个数为1,激活函数选择tanh,参数有41个,总参数为7 360个。
4.2 实验结果与分析
实验采用3个指标来评价模型在测试集上的预测精度,分别是平均绝对误差MAE、平均百分误差MAPE、均方根误差RMSE,它们的计算公式如下(其中Y为模型输出值,![]() 为真实值):
为真实值):
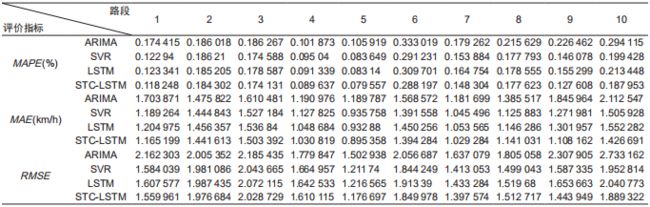
STC-LSTM模型与ARIAM模型、SVR模型、LSTM模型的预测结果见表1。
表1 模型预测结果
Tab.1 Prediction results
从表1速度预测结果来看,不同路段的模型预测精度差别较大,平均百分误差可以低至8%,也可以高达29%,这是因为每条路段的交通变化模式不同,可能存在一定的空间异质性,使得模型对不同的路段预测效果不同。
但综合所有道路,STC-LSTM模型预测结果的MAPE均优于其他模型。STC-LSTM模型预测结果的MAPE平均为15.76%,MAE平均为1.2136 km/h,相比于LSTM模型MAPE平均减少了1.07%,MAE平均减少了0.054 km/h。这说明时空关联度加权的方式对于速度预测起到了作用,可以一定程度上反映路段间交通速度变化的时空特征。
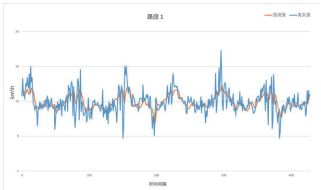
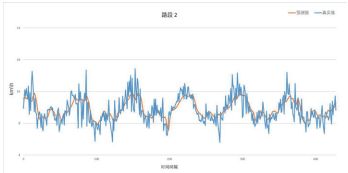
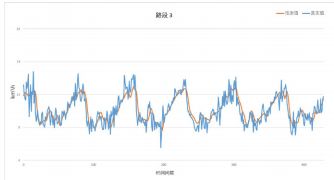
但基于时空关联度加权的LSTM模型的均方根误差在1.17~2.02之间浮动,这说明预测速度有一定偏差。以路段1、2、3为例,结合图4、5、6可知,速度预测值可以反映速度变化的大致趋势,但真实情况的速度波动较大而且频繁,这一点本文提出的模型难以模拟。一方面有可能是真实值记录本身存在误差或者出现异常,不能很好地反映车辆行驶的实际情况;另一方面,这也是大多数预测模型的共同问题,高频波动随机性较强,难以通过学习的方式进行模拟。
图4 路段1预测值与真实值对比
Fig.4 Comparison of prediction value and observed value for road 1
图5 路段2预测值与真实值对比
Fig.5 Comparison of prediction value and observed value for road 2
图6 路段3预测值与真实值对比
Fig.6 Comparison of prediction value and observed value for road 3
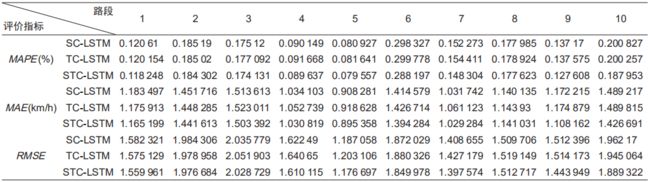
为了进一步探究关联度指标度量方式对预测精度的影响,分别使用时间关联度和空间邻接关系单独进行加权,与时空关联度整体加权(ST)的方法进行比较。STCLSTM模型即为原预测模型,综合考虑空间关联度和时间关联度;SC-LSTM模型(Spatio Correlation Long ShortTerm Memory)为只考虑空间关联度的预测模型,只有关联度w的计算方式与原模型不同;TC-LSTM模型(Temporal Correlation Long Short-Term Memory)为只考虑时间关联度的预测模型。3种模型预测结果见表2。
表2 不同时空特征预测结果
Tab.2 Prediction results of roads with difffferent spatio-temporal patterns of speeds
以表2中MAPE为例,所有预测路段中,STC-LSTM的MAPE均值为0.157 556,而SC-LSTM和TC-LSTM的MAPE均值分别为0.161 857 8和0.162 652,表1中不加权的LSTM的MAPE均值为0.168 336 9。可以看到,时空关联度整体加权的预测精度要优于时间关联度和空间邻接关系单独加权的方法,而时间关联度加权和空间邻接关系单独加权的预测精度要优于不加权的LSTM。逐路段进行对比,结论也大致相同。这表明时间关联度和空间邻接关系都能够对预测起到提升作用,而两者的融合提升更加明显。
5 结束语
交通速度随时间和路段不同而有较大波动,针对交通速度预测问题,本文构建了一种基于时空关联度加权的LSTM模型。该模型挖掘了交通速度在时间和空间上的变化特点,通过时空关联度来量化速度变化在时空上的关联特征,并充分利用了LSTM模型学习长期依赖规律的能力,实现了对交通速度的预测。相比于普通的长短期记忆网络模型,基于时空关联度加权的LSTM模型取得了明显的精度提升,证明了该模型的有效性。
本文设计的交通速度预测模型仍有继续深入研究和改进之处,一方面是数据本身的采样频率限制了预测结果,使得不同路段的模型预测精度差别较大;另一方面是模型对于关联特征在时空上的划分稍有重合,还有待更进一步的探索。
本期回顾
众源地理信息及应用
· 众源地理数据的质量问题与研究进展
· 基于E-WID线/线细分拓扑关系的OSM数据冲突检测
· OSM简单目标增量更新质量控制与评价的自动化方法
理论研究
· 基于百度指数的生态文明关注度时空分析
· “21世纪海上丝绸之路”有向复杂航运网络抗毁性研究
· 基于保形变换和横轴切平面投影的街景影像纠正方法
邮箱变更声明
·《地理信息世界》邮箱变更声明
网站开通公告
·关于开通《地理信息世界》网站的公告
诚聘特约审稿专家
·诚聘|《地理信息世界》诚聘特约审稿专家
专题组稿
·约稿函|《地理信息世界》关于开辟“博士综述论坛”专栏的约稿函