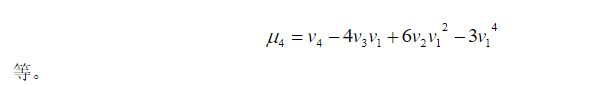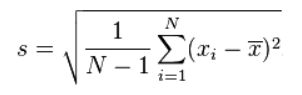统计学—常用统计量
统计学—常用统计量
- 一、均值 μ \mu μ
- 一、样本均值 X ‾ \overline{X} X
- 二、方差 σ \sigma σ
- 二、样本方差 S 2 S^{2} S2
- 三、标准差 σ 2 \sigma^2 σ2
- 三、样本标准差 S S S
- 四、样本的k阶原点矩
- 五、样本的k阶中心矩
- 一、期望
- 三、原点矩
- 四、中心距
- 五、协方差与相关系数
-
- 1、定义
- 2、协方差的性质
- 六、为什么使用标准差？
-
- 贝赛尔修正
- 公式的选择
- 平均值与标准差的适用范围及误用
- 中部单峰：
一、均值 μ \mu μ
$$
一、样本均值 X ‾ \overline{X} X
所有数据之和除以数据点的个数；查看数据的平均水平；
X ‾ = 1 n ∑ i = 1 n X i = x 1 + x 2 + x 3 + . . . + x n n \overline{X} = \frac{1}{n}\sum_{i=1}^{n}X_{i} =\frac{x_{1}+x_{2}+x_{3}+...+x_{n}}{n} X=n1i=1∑nXi=nx1+x2+x3+...+xn
二、方差 σ \sigma σ
σ = 1 N ∑ i = 1 N ( X − μ ) 2 \sigma = \frac{1}{N} \sum_{i=1}^{N}(X-\mu)^2 σ=N1i=1∑N(X−μ)2
二、样本方差 S 2 S^{2} S2
计算方差的目的是为了表示数据集中数据点的离散程度；
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2} S2=n−11i=1∑n(Xi−X)2
三、标准差 σ 2 \sigma^2 σ2
σ 2 = 1 N ∑ i = 1 N ( X − μ ) 2 \sigma^2 = \sqrt{\frac{1}{N} \sum_{i=1}^{N}(X-\mu)^2} σ2=N1i=1∑N(X−μ)2
三、样本标准差 S S S
表示数据点的离散程度；
S = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} S=n−11i=1∑n(Xi−X)2
四、样本的k阶原点矩
A k = 1 n ∑ i = 1 n X i k A_{k} = \frac{1}{n}\sum_{i=1}^{n}X^{k}_{i} Ak=n1i=1∑nXik
五、样本的k阶中心矩
B k = 1 n ∑ i = 1 n ( X i − X ‾ ) k B_{k} = \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\overline{X})^{k} Bk=n1i=1∑n(Xi−X)k
一、期望
1.1 定义
设 P ( x ) P(x) P(x) 是一个离散概率分布，自变量的取值范围为 { x 1 , x 2 , . . . , x n } \{x_{1},x_{2},...,x_{n}\} {x1,x2,...,xn}。其期望被定义为：
E ( x ) = ∑ i = 1 n x k P ( x k ) E(x) = \sum_{i=1}^{n}x_{k}P(x_{k}) E(x)=i=1∑nxkP(xk)
E ( X ) E(X) E(X) 反映了离散型随机变量取值的平均水平。
1.2 性质
（1） E ( a X + b ) = a E ( X ) + b E(aX+b) = aE(X) + b E(aX+b)=aE(X)+b
（2） E ( a X ) = a E ( X ) E(aX) = aE(X) E(aX)=aE(X)
（3） E ( X + b ) = E ( X ) + b E(X+b) = E(X) + b E(X+b)=E(X)+b
（4） E ( b ) = b E(b) = b E(b)=b
（5） E ( b ) = b E(b) = b E(b)=b
（6） E ( f ( x ) ) = b E(f(x)) = b E(f(x))=b
设 P ( x ) P(x) P(x) 是一个连续概率密度函数，其期望为：
E ( x ) = ∫ − ∞ + ∞ x p ( x ) d x E(x) = \int_{-\infty}^{+\infty}xp(x) dx E(x)=∫−∞+∞xp(x)dx
三、原点矩
四、中心距
五、协方差与相关系数
二维随机变量的数字特征中最常用的就是协方差与相关系数。
1、定义
设有二维随机变量 (X,Y) \textit{\textbf{(X,Y)}} (X,Y) ,如果 E[X-E(X)][Y-E(Y)] \textit{\textbf{E[X-E(X)][Y-E(Y)]}} E[X-E(X)][Y-E(Y)] 存在，则称 E[X-E(X)][Y-E(Y)] \textit{\textbf{E[X-E(X)][Y-E(Y)]}} E[X-E(X)][Y-E(Y)] 为随机变量 X \textit{\textbf{X}} X 与 Y \textit{\textbf{Y}} Y 的协方差,记作 cov(X,Y) \textit{\textbf{cov(X,Y)}} cov(X,Y) ，即
cov(X,Y)=E[X-E(X)][Y-E(Y)] \textit{\qquad \qquad \qquad \textbf{cov(X,Y)=E[X-E(X)][Y-E(Y)]}} cov(X,Y)=E[X-E(X)][Y-E(Y)]
而 cov(X,Y) D(X) D(Y) \frac {\textbf{\textit{cov(X,Y)}}} {\sqrt{\textbf{\textit{D(X)}}} \sqrt{\textbf{\textit{D(Y)}}}} D(X)D(Y)cov(X,Y) 称为随机变量 X \textit{\textbf{X}} X 与 Y \textit{\textbf{Y}} Y 的相关系数，记作 R(X,Y) \textit{\textbf{R(X,Y)}} R(X,Y) ,即
R ( X , Y ) = c o v ( X , Y ) D ( X ) D ( Y ) = c o v ( X , Y ) σ ( X ) σ ( Y ) R(X,Y) = \frac {cov(X,Y) }{\sqrt{D(X)} \sqrt{D(Y)} } = \frac {cov(X,Y) }{\sigma(X) \sigma(Y) } R(X,Y)=D(X)D(Y)cov(X,Y)=σ(X)σ(Y)cov(X,Y)
显然，协方差 cov(X,Y) \textbf{cov(X,Y)} cov(X,Y) 是 X \textbf{X} X 和 Y \textbf{Y} Y 的二阶混合中心矩。
当 cov(X,Y)=0 \textbf{cov(X,Y)=0} cov(X,Y)=0 ，通常称随机变量 X \textbf{X} X 与 Y \textbf{Y} Y 是不相关的。
2、协方差的性质
1） c o v ( X , Y ) = c o v ( Y , X ) c o v ( X , X ) = D ( X ) cov(X,Y)=cov(Y,X) \\ \ \ \ \ \ cov(X,X)=D(X) cov(X,Y)=cov(Y,X) cov(X,X)=D(X)
由定义知 性能（1）是显然的。
2） c o v ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) cov(X,Y)=E(XY)-E(X)E(Y) cov(X,Y)=E(XY)−E(X)E(Y)
六、为什么使用标准差？
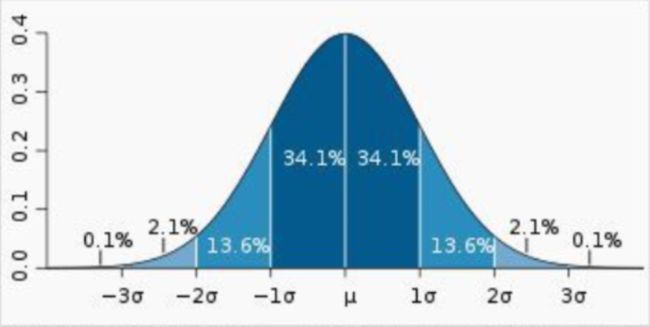
深蓝区域是距平均值小于一个标准差之内的数值范围。在正态分布中，此范围所占比例为全部数据量的68%。根据正态分布，两个标准差之内（深蓝，蓝）的数据量合起来所占比例为95%。根据正态分布，三个标准差之内（深蓝，蓝，浅蓝）的数据量合起来所占比例为99%。
所有数减去其平均值的平方和，所得结果除以该组数之个数（或个数减一，即变异数），再把所得值开根号，所得之数就是这组数据的标准差。
标准计算公式：
假设有一组数值X₁,X₂,X₃,…Xn（皆为实数），其平均值（算术平均值）为μ，公式如图1。
标准差也被称为标准偏差，或者实验标准差，公式为
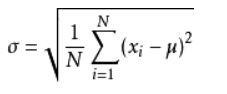
例如，A、B两组各有6位学生参加同一次语文测验，A组的分数为95、85、75、65、55、45，B组的分数为73、72、71、69、68、67。这两组的平均数都是70，但A组的标准差约为17.08分，B组的标准差约为2.16分，说明A组学生之间的差距要比B组学生之间的差距大得多。
一个标准差 68%， 两个标准差 95%, 三个标准差 99%。
与方差相比，使用标准差来表示数据点的离散程度有3个好处：
- 表示离散程度的数字与样本数据点的数量级一致，更适合对数据样本形成感性认知。依然以上述10个点的CPU使用率数据为例，其方差约为41，而标准差则为6.4；两者相比较，标准差更适合人理解。
- 表示离散程度的数字单位与样本数据的单位一致，更方便做后续的分析运算。
- 在样本数据大致符合正态分布的情况下，标准差具有方便估算的特性：66.7%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内，而99%的数据点将会落在平均值前后3个标准差的范围内。
贝赛尔修正
在上面的方差公式和标准差公式中，存在一个值为N的分母，其作用为将计算得到的累积偏差进行平均，从而消除数据集大小对计算数据离散程度所产生的影响。不过，使用N所计算得到的方差及标准差只能用来表示该数据集本身(population)的离散程度；如果数据集是某个更大的研究对象的样本(sample)，那么在计算该研究对象的离散程度时，就需要对上述方差公式和标准差公式进行贝塞尔修正，将N替换为N-1：
经过贝塞尔修正后的方差公式：
经过贝塞尔修正后的标准差公式：
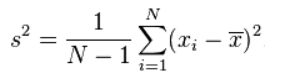
公式的选择
是否使用贝塞尔修正，是由数据集的性质来决定的：如果只想计算数据集本身的离散程度(population)，那么就使用未经修正的公式；如果数据集是一个样本(sample)，而想要计算的则是样本所表达对象的离散程度，那么就使用贝塞尔修正后的公式。在特殊情况下，如果该数据集相较总体而言是一个极大的样本 (比如一分钟内采集了十万次的IO数据) — 在这种情况下，该样本数据集不可能错过任何的异常值(outlier)，此时可以使用未经修正的公式来计算总体数据的离散程度。
平均值与标准差的适用范围及误用
大多数统计学指标都有其适用范围，平均值、方差和标准差也不例外，其适用的数据集必须满足以下条件：
中部单峰：
-
数据集只存在一个峰值。很简单，以假想的CPU使用率数据为例，如果50%的数据点位于20附近，另外50%的数据点位于80附近（两个峰），那么计算得到的平均值约为50，而标准差约为31；这两个计算结果完全无法描述数据点的特征，反而具有误导性。
-
这个峰值必须大致位于数据集中部。还是以假想的CPU数据为例，如果80%的数据点位于20附近，剩下的20%数据随机分布于30~90之间，那么计算得到的平均值约为35，而标准差约为25；与之前一样，这两个计算结果不仅无法描述数据特征，反而会造成误导。
遗憾的是，在现实生活中，很多数据分布并不满足上述两个条件；因此，在使用平均值、方差和标准差的时候，必须谨慎小心。
如果数据集仅仅满足一个条件：单峰。那么，峰值在哪里？峰的宽带是多少？峰两边的数据对称性如何？有没有异常值(outlier)？为了回答这些问题，除了平均值、方差和标准差，需要更合适的工具和分析指标，而这，就是中位数、均方根、百分位数和四分差的意义所在。