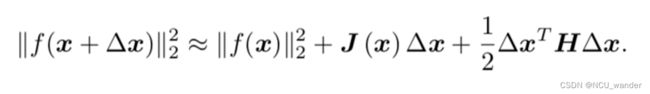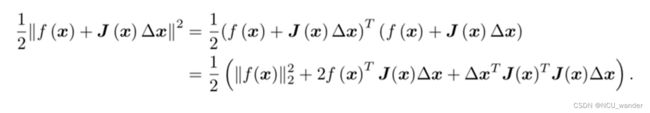最小二乘、梯度下降与反向传播

在阅读高翔博士的slam十四讲的过程中，有关于求解观测与估计值的最大似然问题引起了我比较好的好奇，并且顺着这个问题了解了自己之前一直困惑的梯度下降问题以及高斯牛顿方法，在此进行总结。

1、前序

1.1 贝叶斯公式

首先问题是由作者根据贝叶斯法则将后验分布经过变换转为最大似然问题来解决的，直接求后验分布是困难的，但是求一个状态最优估计，使得在该状态下后验概率最大化，则是可行的。

p(x,y | z,u) = p(z,u | x,y) * p(x,y) / p(z,u)
p(z,u | x,y) :最大似然  p(x,y)：先验分布

那么先验分布与后验概率的区别是什么呢？

贝叶斯公式：P(Y|X) = P(X|Y)*P(Y)/P(X)

先验概率(prior probability)：这个概率是通过统计得到的，或者依据自身依据经验给出的一个概率值，这里P(Y)就是先验概率；
后验概率：根据观察到的样本修正之后的概率值，这里P(Y|X)就是后验概率。

可以参考先验概率与后验概率（贝叶斯公式）对贝叶斯公式相关概念进行理解。

1.2 最小二乘

最小二乘的相关知识可以说一直以来都是见于诸多文章的，也是深度学习乃至于机器学习整个的入门算法，对于最小二乘算法的求解公式却一直关注不大，最基本的算法其实就包含了最主流实用的解决方法。
最小二乘问题的四种解法——牛顿法，梯度下降法，高斯牛顿法和列文伯格-马夸特法的区别和联系

注意问题的求解核心在于对增量的求导；求得合适的增量达到一阶导数数值为零，从而达到极值点。下面我们好好解释这一点，来明确如何通过对增量求导的方式来得到最小二乘的求解。

首先明确一下，我们将许多问题转化为最小二乘问题之后，接下来实质上就是最小二乘的数值优化问题；给定的（x，y）数据组之后，求解的方程组变量就是我们要求解的模型权重，那么我们关心的增量其实也是权重的增量。这部分内容在slam优化也有非常多的应用，可以参考slam十四讲第六节的相关内容。

首先是最简单的梯度下降法，梯度下降法是基于以下的观测原理而来的：
如果实值函数$f(x)$在点 $x=a$ 处可微且有定义，那么函数$f(x)$在点 $x=a$ 处，沿着梯度的反方向下降的最快。实际使用中考虑到合理设置步长，尽量避免优化曲线过于曲折。

def optimizer(data,starting_a,starting_b,learning_rate,num_iter):
    a = starting_a
    b = starting_b
    # 梯度下降
    for i in range(num_iter):
        # 朝梯度下降的方向更新a，b
        a,b =compute_gradient(a,b,data,learning_rate)
        if i%100==0:
            print('iter {0}:error={1}'.format(i,compute_error(a,b,data)))
    return [a,b]

def compute_gradient(a_current,b_current,data,learning_rate):
    N = float(len(data))
    x = data[:,0]
    y = data[:,1]
    a_gradient = -(2/N)*(y-b_current*x-a_current) #求解梯度的公式，可推导
    a_gradient = np.sum(a_gradient,axis=0)
    b_gradient = -(2/N)*x*(y-b_current*x-a_current)
    b_gradient = np.sum(b_gradient,axis=0)
    
    new_a = a_current - (learning_rate * a_gradient) #对待求解的权重进行梯度下降，不断更新新的梯度值
    new_b = b_current - (learning_rate * b_gradient)

    return [new_a,new_b]

在偏直观的梯度下降之后，也有理论解释的手段：可以直接对最小二乘的公式做泰勒展开，得到：

注意此时的x实质上是我们待求解的模型权重，那么每次迭代的权重增量应该如何选取呢？每次选取合理的权重增量使得其可以逐步接近我们想要的最优解。将其视作完全的函数求解问题，我们知道函数一阶导为零时可以得到此状态下的极值点，则将上式针对增量求导。

则可以得到下一步应该迭代的增量数值。这个方法就是牛顿法。

在牛顿法之后，牛顿法因为海塞矩阵的问题，引入了计算量巨大且不一定存在的二阶导数等等问题，因此研究人员又提出了高斯牛顿法。相比较于牛顿法对最小二乘优化函数做泰勒级数开展，高斯牛顿是对待优化函数$f(x)$先做一阶的泰勒展开，再将其转化为最小二乘问题，泰勒展开只到一阶，也就意味方法不那么精确。

对增量求导，之后得到下一步迭代的增量数值。

最后感叹一下，高斯牛顿和梯度下降自己之前一直一知半解，这一次机缘巧合花了一番力气来了解，或许仍然有不足之处，但亦为点滴进步。

2、梯度下降

梯度下降作为深度学习中的一种常见的优化算法，中心思想是沿着目标函数梯度的方向更新参数值以希望达到目标函数最小（或最大）。当然在很多其他场合也会用梯度下降法，例如前面叙述中提到的最小二乘也是可以用梯度下降作为解决方法的。
梯度下降在深度学习的海量数据情况下，延伸出一些兼顾学习速度与精度的变形形式，根据每次取用数据量的不同我们将梯度下降法分为以下三类：
详解批量梯度下降法（BGD）、随机梯度下降法（SGD）和小批量梯度下降法（MBGD）

以Mini-Batch Gradient Descent为例，我们在使用的过程中，首先从全部样本中选取mini batch数量的样本作为本次权重更新的数据（img1-n），每一张img会提取相应的特征，假设最终出现在loss function内的特征数量为m，loss function就是关于分别针对关于x1，x2 — xn的m个维度分别求取梯度，对这个m个梯度求取反方向之后合并为最终的下降向量，向量的方向与大小遵从矢量相加的原则。

3、反向传播

由于深度学习网络按层深入，层层嵌套的特点，对深度网络目标函数计算梯度的时候，需要用反向传播的方式由深到浅倒着计算以及更新参数。所以反向传播法是梯度下降法在深度网络上的具体实现方式。

CHAPTER 2How the backpropagation algorithm works

反向传播，（随机）梯度下降

4、正则化

在查询以上知识的过程中接触到正则化相关知识，对其进行可进行总结
L1,L2正则化