正则化综述（L2\L1正则化、弹性网络正则化，数据增强、k折交叉验证、dropout、early stopping、injecting noise）

首先，我们来对要了解的正则化方法做一个概览:

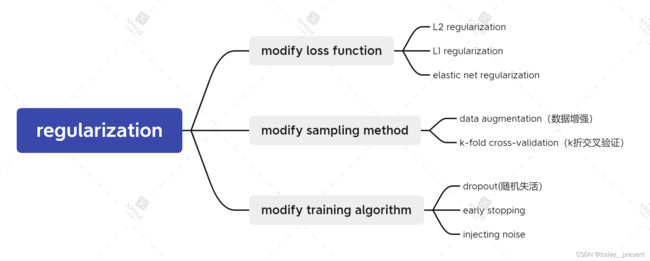
首先从损失函数后添加正则项方面，有L2正则化、L1正则化和elastic正则化；
从采样方法改进方面，有数据增强，k折交叉验证等方式；
从训练算法改进方面，有的随机失活，早停法，以及导入噪声等方式。
我们将首先了解一下正则化方式的基本思想，其次了解一下正则化的一些具体方法，比如基于验证集的处理，参数范数惩罚等。
首先是第一部分：

过拟合概述与正则化思想

首先我们来简单过一下正则化方法要解决的问题：过拟合。

上图展示了一个分类的模型，绿色的线表示过拟合的状态，黑色的线表示正常模型的状态。我们可以看到，绿色的线虽然在训练集中表现得非常好，几乎把所有的点都分到了正确的区域，但如果将此模型应用于其他的数据中，模型的表现就会变差了。
过拟合是在模型参数拟合过程中由于训练数据包含抽样误差，在训练时复杂的模型将抽样误差也进行了拟合导致的。所谓抽样误差，是指抽样得到的样本集和整体数据集之间的偏差。
下面我们来引入正则化的概念。

正则化，也就是Regularization的目的是使模型性能更趋于稳定可靠。在这次讲解中，我们采取了广义的正则化的范畴，指正则化操作不仅限于添加正则化项，所有有利于模型稳定可靠（提升泛化能力，降低结构风险）的方法都可以认为是正则化；数据、模型、训练方法等一系列操作都分布着正则化方法。从这个角度，归一化操作也可以被看做是一种正则化方法。

我们来通过一个小问题作为例子理解正则化的思想。

对于一个正弦回归问题，我们根据十个数据点的情况，进行神经网络的训练。如图所示我们可以看到神经网络的结构，输入层、隐藏层和输出层。

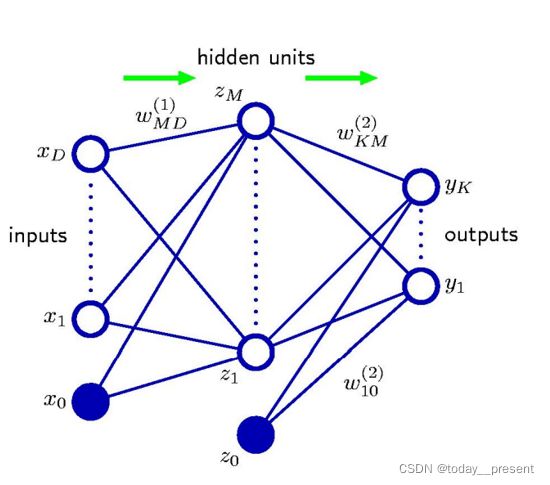
而在隐藏层的神经元数，也就是hidden units的数目分别是1,3，10的时候，我们通过神经网络训练，分别得到了如左图所示的三种模型情况。

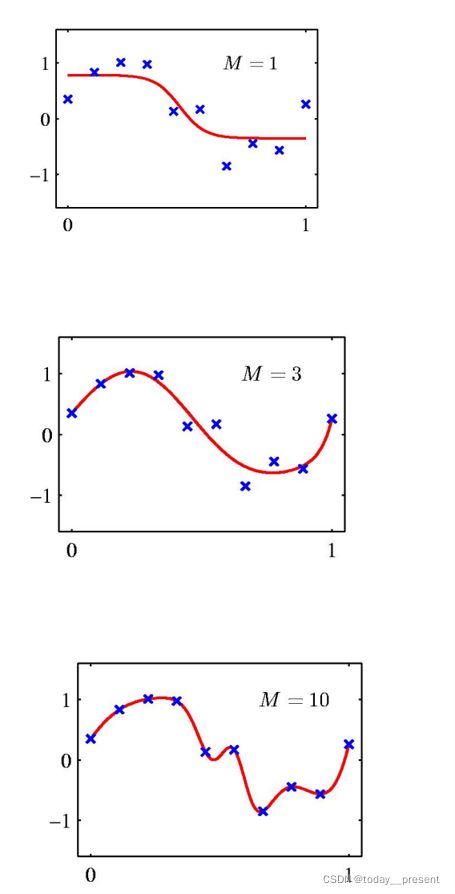
我们可以观察到，对于正弦回归问题来讲，隐藏神经元数M为1时，表现为欠拟合；M为3时，模型比较接近于真实水平；而在M为10时，表现为过拟合。

对于正弦回归问题，我们可能已知了实际模型的情况。但是如果是在实际的神经网络的模型训练过程中，这个隐藏神经元的数量，也就是M的数值，到底该如何确定，才不会让模型更接近实际水平呢？
容易想到的是一种方式是，我们将数据分为训练集与验证集，从而对每个可能的M，在训练集上进行训练之后，测算模型在验证集的表现，从而确定隐藏单元数M的数值。

K折交叉验证（k-fold cross-validation）

关于将数据分成训练集与验证集的过程，我们引入k折交叉验证：

k折交叉验证（k-fold cross-validation），是指将训练集分割成k个子样本，一个单独的子样本被保留作为验证模型的数据，其他k − 1个样本用来训练，如右图所示，重复k次验证，每个子样本验证一次，平均k次的模型结果或者使用其它结合方式，最终得到一个单一估测模型。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10次交叉验证是最常用的。

早停法（early stopping）

我们再回到上面的这个问题。我们将不同的隐藏单元，也就是M值为横坐标的情况下，计算验证集的误差情况。

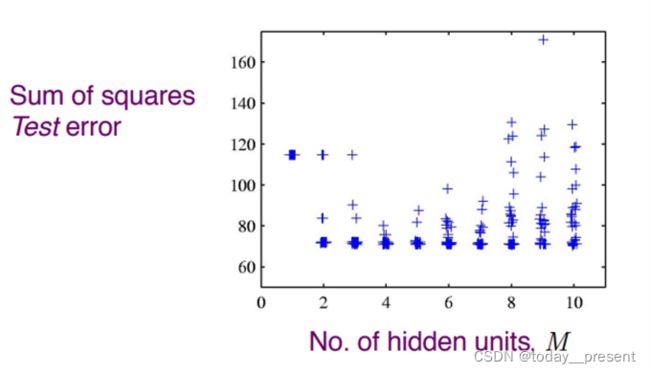
可以看出，误差的整体情况随着M值的增大，是成谷形先下降后上升的，也就是在此过程中，模型从欠拟合的状态逐渐变成了过拟合的状态。于是我们可以想见，倘若找到模型的这个从下降变为上升的拐点，在此停止训练，那么既可以省下资源，还可以避免继续训练导致过拟合的问题。这与我们下面所要介绍的early-stopping，也就是早停法的原理非常类似。

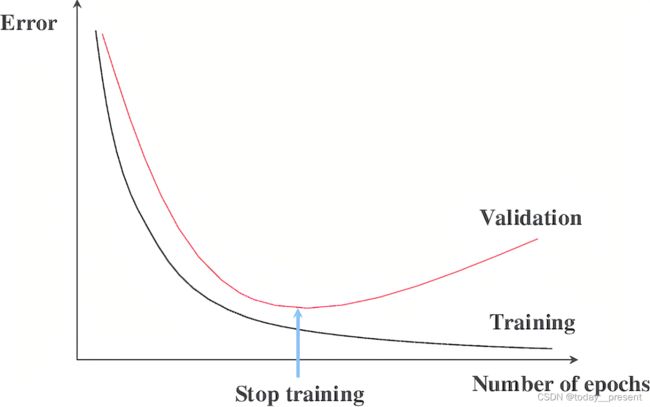
上图展示了随着epoch的次数增加，训练集与验证集的误差变化情况。Epoch指的是所有的数据送入网络中，完成了一次前向计算 + 反向传播的过程。那么由这张图我们可以看出，随着迭代次数的增多，训练集的拟合程度一直呈提升状态，表现为误差稳步降低，但在验证集上却并非如此。在经过某一点后，模型在训练集上的表现开始变差，表征了模型的泛化程度降低，模型过拟合了。于是我们引入早停法的基本概念：
早停法的基本含义是在训练中计算模型在验证集上的表现，当模型在验证集上的表现开始下降的时候，停止训练，这样就能避免继续训练导致过拟合的问题。其主要步骤如下：

1. 将数据集划分成训练集和验证集；
2. 只在训练集上进行训练，并每个epoch(或N个epoch）计算一次模型在验证集上的误差，当模型在验证集上的误差开始回升的时候停止训练；
3. 使用上一次迭代结果中的参数作为模型的最终参数。

当然，左图所展示的误差状况只是理想情况下的，在实际训练中，误差的表现还会出现反复等状况，而我们需要在优化损失函数的同时，兼顾防止过拟合的问题，所以也出现了许多停止标准，模型在何时停止这个问题变得比较复杂。
除上面的early stopping方法之外，还有一类方法来降低模型的复杂度：在上面的小问题中，我们选择相对较大的隐藏神经元的数量M，不再限制M的数值，而是通过添加正则化项来控制复杂性。
其中的一大类方式便是

参数范数惩罚（Parameter Norm Penalty）

L2正则化

首先是L2正则化：

超参数指被每一轮训练手动调整的参数，而不是训练得到的，其意义类似于我们之前提到的隐藏神经元数M。
直观地说，我们可以将回归视为一个额外的惩罚项或约束，如右图所示。没有正则化的情况下，我们的目标是找到全局的成本最低。通过增加正则化项，我们的目标是在必须保持在（灰色阴影球）范围内的约束下最小化损失函数。

L1正则化

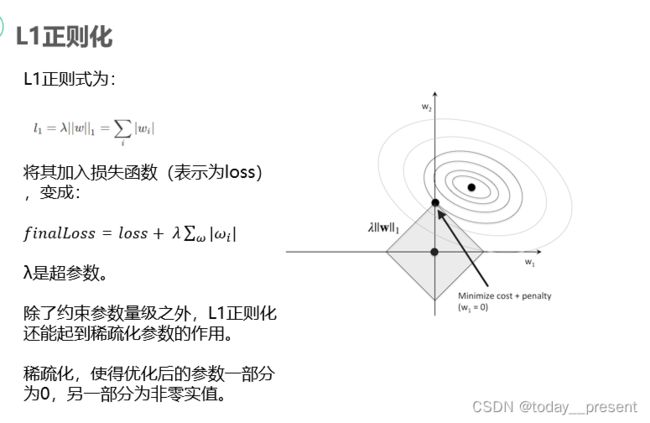与L2类似的，我们需要在一定范围内最小化损失函数，但不同的是，因为这次的正则化项是权重的绝对值，所以是在如图所示的方形区域内最小化损失函数。根据图中的情况我们可以推测，常常会在方形区域的顶点处取到最优值，而顶点在坐标轴上，这就有助于权重的稀疏化。所以，如果已知模型中的很多变量为无关变量，我们倾向于选择L1正则化，从而使得拟合模型更加简洁和便于解读。
但如果模型中有非常多的变量，我们无法知道其是否是无关变量，如基于10000个基因的表达预测小鼠体积。在这种情况下，我们应该选择L2正则化，还是L1正则化呢？

弹性网络正则化（elastic net regularization）

答案是弹性网络正则化。简单来说，弹性网络回归是lasso回归和岭回归的结合版本，而elastic网络正则化，即为L1正则化+L2正则化。将L1的正则化和L2的正则化联合使用，得到正则化式：

其他方式

上面所介绍的L1，L2正则化和elastic网络正则化都是传统机器学习中非常常用的正则化方法，但是，在训练神经网络时，这种参数范数惩罚的效果往往不如在传统机器学习模型中的显著，所以训练深度学习模型时，往往还会使用其它正则化方法，比如前面所提到的早停法，就是其中的一种。
下面我们来介绍另外的几种。

随机失活（dropout）

原理：
对于某层的每个神经元，在训练阶段均以概率p随机将该神经元失活，也就是将其权重置零，以缓解神经元之间隐形的协同适应，从而降低模型的复杂度。
测试阶段所有神经元都呈激活态，权重乘以1/ (1−p)。
需要注意的是，随机失活过程只针对全连接层进行操作
虽然dropout之后的网络只是原网络的一个子网络，复杂度不比原网络。但由于每个神经元的dropout是 随机dropout，因此每一轮都相当于在一个新的子网络上训练。那么最终得到的模型便是无数个子网络共同训练 的成果，效果自然会更好。
然后麻烦也来了，训练阶段的每个神经元要事先添加一道概率流程：


也就是说，在这里的公式变换里，为了便于计算，我们设置神经元以1-p概率失活，以p概率留存，从而我们对隐藏神经元输出的结果以概率1-p置零，就是将这里的y向量乘以一个系数向量r，而所乘的系数rj向量的分量服从伯努利分布。

传统神经网络中，由于神经元间的互联，对于某单个神经元来说，其反向传导来的梯度信息同时也受到其他神经元的影响，可谓“牵一发而动全身”。这就是所谓的“复杂协同适应”效应。随机失活的提出正是一定程度上缓解了神经元之间复杂的协同适应，降低了神经元间依赖，避免了网络过拟合的发生。

Dropout在约束网络复杂度的同时，还是一种针对深度模型的高效集成学习方法，能够降低神经元之间的依赖。随机失活是目前几乎所有配备全连接层的深度卷积神经网络都在使用的网络正则化方法。

最大范数约束（max norm constraints）

对于每一个神经元 Max-Norm Regularization 的目的在于限制输入链接权重的大小。
更小的权重参数有利于模型对噪声的鲁棒性，这里限制参数的大小目的就是如此。在实践中将 Max-Norm Regularization 结合dropout 使用一般效果将会更好。

注入噪声（Injecting noise ）

与dropout类似的，这个方法通常用于神经网络中。在这个方法中，我们在反向传播对学习的权重进行更新的过程中，少量随机噪声被添加到更新后的权重中，以使其更鲁棒或对微小变化不敏感，这有助于模型构建更稳健的特征集，从而确保模型不会过度拟合训练数据。然而，作为正则化方式之一，这种方法并没有取得很好的效果。

数据增强（data augmentation）

1. 几何变换类：翻转、旋转、缩放、裁剪、移位
2. 颜色变换类：高斯噪声、模糊、颜色变换、擦除、填充等
3. 多样本数据增强等高级增强方法