组合逻辑中的 竞争冒险问题

---

电路中组合逻辑的竞争问题是老生常谈的问题

除了本文外，还可参考

1. 竞争 导致冒险

● 竞争：指组合逻辑电路中，多个输入信号变化传输到同一个门级电路时，在时间上有先有后的现象。

● 冒险：既然电平到达有先有后，如果一端信号先到达，另一端信号还未到达，此时组合电路输出就会出现瞬时的中间态。这个中间态有可能是瞬时的高电平，即尖峰脉冲。

即竞争可能导致冒险，然而容易引起竞争的原因是线路延迟

与逻辑简单程序如下：

module test(input [2:0] a, input [2:0] b, output [2:0] y);
	assign y = a & b;
endmodule

a和b信号到达与门延迟不同，就是竞争现象。

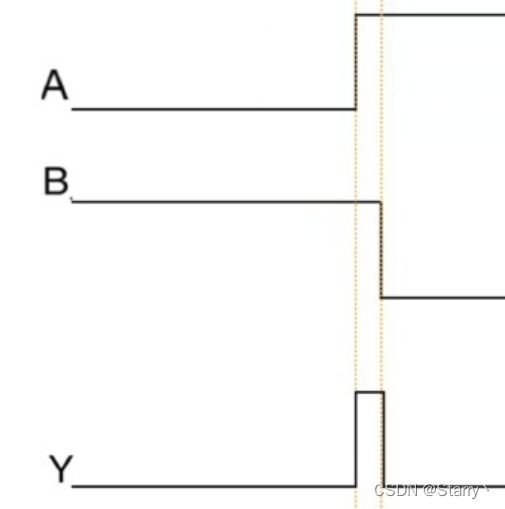
而这种竞争现象，可能会使Y出现瞬时脉冲，这就是冒险现象。

如当a由0变1，b由1变0时。如果由于线长短原因，a比b先到达，即a已经为较高电平了，b还维持较高电平，输出y就可能出现尖峰脉冲。

除了电路中有信号先后到达的问题，仿真中也有竞争问题。

1.1. 测试仿真的 竞争问题

仿真波形图中，posedge clk往往与信号变化对齐，那到底采样的是变化前的值还是变化后的值？

如下图所示，黄线处，分别用clk1和clk2采样，采样的d1的值是多少呢？看是看不出来的

1. 如果clk1驱动clk2和d1，则黄线处：clk1采样d1为01，clk2采样d1为02。
2. 如果clk2驱动clk1和d1，则黄线处：clk1采样d1为02，clk2采样d1为01。

出现不同取值的原因在于，仿真波形会默认在驱动信号和被驱动信号波形之间增加大小为delta cycle的延迟，且delta cycle → 0，只有放大才能看出来时序关系，如下图

实际硬件中，delta cycle其实是时钟产生posedge clk到触发器Q端输出的时间，后文会讲怎么算，非常小而且仿真软件并不知道硬件时间是多少。

综上所述

仿真中竞争问题：波形无法表达时钟和信号间的驱动关系。若是在时钟处采样，也无法判定采样的结果是时钟前的值还是时钟后的值。

下面给出解决办法

放大delta cycle

驱动时钟和被驱动信号在时间上存在着delta cycle的延迟，仿真波形中看不出来，所以为了方便起见解决方法是

放大delta cycle至肉眼可见，体现驱动信号的前后关系

例如clk驱动某个寄存器，就将寄存器输出整体右移即可，如下图

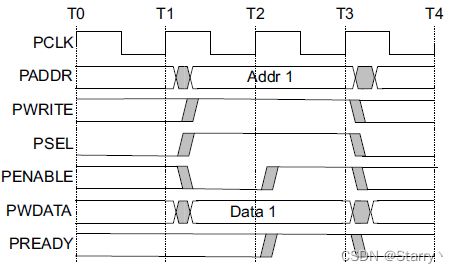
可以清晰看出每个posedge clk采样的是什么值，驱动的是什么值

而Systemverilog中interface子程序中的clocking块就是干这个用的

SV中的采样和数据驱动
RTL仿真时信号竞争问题——通过delta-cycle查看严格的时序逻辑前后关系
Systemverilog（绿皮书）第四章——连接设计（二）采样与数据驱动
clocking时钟块消除采样时信号竞争 —SV,systemverilog

2. 判断竞争：逻辑门输入是否直连 相同逻辑

再回到电路的组合逻辑中来，下面给出组合逻辑竞争的判断方法。

一个逻辑门有两个输入

如果这两个输入直连的逻辑（无论时序逻辑还是组合逻辑）相同，就不会竞争，否则就存在竞争。

module adder(
	input clk,
	input A,
	input B,
	input C,
	output reg Y);
//...
always@(posedge clk) begin
	//...
	Y <= A & B | C;	
end
//...

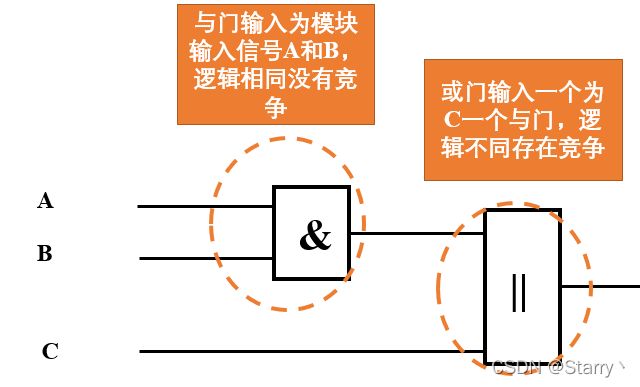
● A & B：与门，需判断A与B的来源逻辑是否相同。若A和B同时输入到adder模块中，则该与门就不存在竞争。

● +C：或门，需判断C与A & B的结果是否来自同一逻辑。若A、B和C同时输入到adder模块中，则该或门存在竞争。

2.1. 判断竞争：局部直连逻辑判断

那么问题来了，对于一串组合逻辑表达式，怎么判断每个逻辑门都是否存在竞争呢？

方法很简单，如果某逻辑门的两个输入直连的是 相同的门or寄存器or变化相同的输入信号，则该逻辑门不会出现问题，就算有问题，也不是这个逻辑门的问题。

例如

Y = A & B | C;

若A、B和C同时变化。先看与门，与门输入直连的是两个相同时间变化的信号，所以不存在竞争。而或门一个输入连的是与门，一个连的是信号C，因此该与门可能存在竞争。

再如

Y = (A' & B) | (A & C);

若A、B和C同时变化。先看或门，或门输入直连的是两个与门，所以不存在竞争。再看A & C这个与门，相连的两个输入信号，所以不存在竞争。再看A' & B的与门，一个连的是信号B，一个连的是非门，所以该与门可能存在竞争

注意此处是说局部直连逻辑不同，是可能存在竞争，还需计算机软件进一步分析。

3. 消除竞争：逻辑门输入直连 相同逻辑

上面其实已经说的很清楚了，只需保证每个逻辑门的输入均直连相同的逻辑，就会消除竞争。

上图中与门直连一个寄存器、一个非门，那么就存在竞争。

为了使与门直连逻辑相同，那么加装两个寄存器，就会消除 竞争。

其实不一定非要加装寄存器，平衡组合逻辑也可以，例如

Y <= (A & B) | C;					//或门存在竞争
Y <= (A & B) | (C & 1'b1);			//或门不存在竞争

3.1. 锁存器

都说写代码的时候if语句要把else写全，case语句要写default，为啥？为了避免锁存器Latch的产生。

那产生个Latch又咋地了？这里分析下

以下面这个代码为例，en为1时q为1’b1，en为0时q锁存。

always@(*)
	if(en)
		q = 1'b1;

得到逻辑表达式为q = en + (en)'·q，然后用上面讲的方法分析这个表达式呗。

与q直连的是或门，或门输入一个是en、另一个是与门，因此可能会存在竞争。

那么锁存器会因此存在冒险嘛？看样子是有可能的，下面分析下。

危害：锁存瞬态值

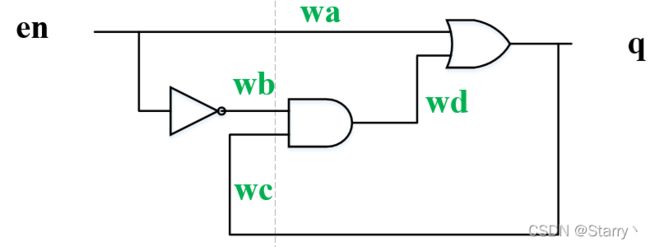
综合出来的电路图如下，并为各导线标注：

首先，稳定时令wa=en=1;wb=(en)'=0;wc=q=1;wd=0;

然后我们让en=1→0;，那么信号传输是有延迟的，所以wa一定先于wb、wc、wd变化，故wa=1→0;，因此对于q来说第一个变化一定是q=1→0;

然后非门才变化完成，即wb=0→1;那么此时wc是多少？是原值1还是新值0？分类讨论

● 电平变化先后为：wa（1→0）、wb（0→1）、wc（1→0）

如果是这样的话，会存在wb=1;wc=1;的中间态，再经过与门wd=0→1，因此会有q=0→1

wb变完之后，wc再变化，最终会有wb=1;wc=0的状态，因此q又有q=1→0;

● 电平变化先后为：wa（1→0）、wc（1→0）、wb（0→1）

如果是这样的话，会存在wb=0;wc=0;的中间态，再经过与门wd=0→1，因此q还是0

wc变完之后，wb再变化，最终会有wb=1;wc=0的状态，因此q保持为0

由此可见最终的输出居然是0，甚至还可能出现个毛刺1。直接看代码无论如何都想不到这个结果。

根本原因在于含有锁存器的电路会有一条导线将输出和某个输入直接相连。

如果出现竞争，那么瞬态的异常电平会被锁存（上面电路中，当wa=1→0而wb仍为0的异常瞬态，就被q捕捉到并通过wc反馈到输入）

如果是时序电路就不会捕获这个异常瞬态。

因此Latch的最大缺陷倒不是毛刺，而是捕获瞬间出现的异常状态并锁存，导致实际输出难以预料